Цыпкин Я.З Основы теории автоматических систем
Подождите немного. Документ загружается.


282
УСТОЙЧИВОСТЬ
НЕЛИНЕЙНЫХ
СИСТЕМ
[ГЛ.
17
устойчивости состояния равновесия нелинейной системы с неста-
ционарной
нелинейной характеристикой можно сформулировать
в
следующей форме.
Частотный
критерий
III
(круговой
критерий).
Состояние
равновесия
х
с
= 0
нелинейной
системы
с
нестационарной
нелинейной
характеристикой
будет
абсолютно
устойчивым,
если
характеристика
нелинейного
элемента
<&(xj)
при
всех t
принадлежит
сектору
(г,
k
0
)
или,
что то
же,
если
коэффициент
статической
линеаризации
k^{x,
t) при всех t
принадлежит
полосе
(г,
k
0
),
а
частотная
характеристика
линейной
части
W(/co),
не
пересекая
(ko,
г)-окружности,
охватывает ее в
положительном
направлении,
т.
е.
против
часовой
стрелки,
sJ2
раз, где
s
H
-»
индекс
неустойчивости
(рис. 17.11, а).
В
частном
случае,
если
s
H
= 0, то
W(j(o)
не
должна
охва-
тывать
(k
0
,
r)-окружность
(рис.
17.11,6).
§
17.7. Общий критерий устойчивости процессов
Уравнение свободного процесса, определяющее устойчивость
вынужденного процеса
x
B
(t),
отличается от уравнения свобод-
ного процесса (17.6), определяющего устойчивость состояния
равновесия
х
с
= 0, лишь конкретизацией нестационарной нели-
нейной
характеристики. Поэтому для установления критерия
устойчивости вынужденного режима можно воспользоваться ча-
стотным критерием III (круговым частотным критерием). Рас-
смотрим условия принадлежности
W(x
c
(t),t)
сектору (г, ko)
Подставляя выражение для
}
¥(x
c
(t),
t) из (17.7), получим
W(0,
/)
=
Ф(х
с
(/))-Ф(х
с
(0)-0,
Ф
(*с
(о
+
х
в
(0)
-
Ф
(х
в
(0)
,
г
<•
х~Щ
°'
Но
для любой кусочно-непрерывной функции
Ф(«с(0+*'
е
(;))-Ф(*'(0)
я ф
,
(
^
С (/))) (17#93)
где
О^б
1
^!.
Поэтому второе из условий (17.92) эквивалентно
условию
г<Ф'(*
с
(О)</го-
(17.94)
Но
c
(0)
(17.95)

17.3]
ОБ
УСТОЙЧИВОСТИ «В МАЛОМ» И «В БОЛЬШОМ»
283
представляет собой коэффициент дифференциальной линеариза-
ции.
Значит, условие принадлежности
W(x
c
,
t) сектору
(г,
ko)
эквивалентно
условию принадлежности коэффициента дифферен-
циальной
линеаризации нелинейного элемента
k^(x
n
(t))
полосе
(г,
ko).
Таким образом, критерий абсолютной устойчивости про-
цессов,
или критерий абсолютной устойчивости нелинейных си-
стем, можно сформулировать в следующей форме.
Частотный
критерий IV (круговой
критерий).
Вынужден-
ные
процессы
в
нелинейной
системе
будут
абсо
гютно
устой-
чивыми,
если
производная
характеристики
нелинейного
элемента
Ф'(х)
или,
что то
же,
коэффициент,
дифференци-
альной
линеаризации
k^(x)
принадлежит
полосе
(г,
ko)
и
частотная
характеристика
линейной
части
W(/со),
не пе-
ресекая
(ko,
r)-окружности,
охватывает
ее в
положитель-
ном направлении,
т.
е.
против
часовой
стрелки,
s
H
/2
раз,
где
s
u
—
индекс
неустойчивости
(рис.
17.11,а).
В
частном
случае
при
s
H
= О
частотная
характеристика
линейной
части
W(jco)
не
должна
охватывать
(k
0
,
r)-
окружность
(рис.
17.11,6).
Круговые критерии (критерии III, IV) по своей формулиров-
ке
аналогичны обычному частотному критерию устойчивости ли-
нейных
систем, но теперь роль точки
(
г-,
/0) или также отрезка
(ko,
г)
играет
(Аг
0
,
г)
-окружность
(рис.
17.12). Требования абсолют-
ной
устойчивости нелинейных си-
стем более жесткие, чем требования
устойчивости линейных систем. Так,
для частотной характеристики /
(рис.
17.12)
линейная система
будет
устойчива, тогда как об абсолют-
ной
устойчивости нелинейной систе-
мы ничего сказать нельзя, так как
все критерии абсолютной устойчивости являются лишь доста-
точными.
§
17.8, Об устойчивости «в малом» и «в большом»
Рассмотрим нелинейную систему с произвольной характери-
стикой
нелинейного элемента
Ф(х)
(рис. 17.13). Представим
Ф(х)
в виде
ф()
Ф'(0)
Рис.
17.12.
где
бФ(л:)
содержит степени х не ниже второй. Используя
обозначение коэффициента дифференциальной
линеаризации,

284
УСТОЙЧИВОСТЬ НЕЛИНЕЙНЫХ СИСТЕМ
1ГЛ.
17
запишем
Ф(х)
в
виде
ф
(
х
)
=
&<
д
>
(0)
х +
6Ф
(х).
(17.96)
Предположим,
что
линеаризованная система,
в
которой
Ф(х)
заменено
на
k№(Q)x,
устойчива.
Это
значит согласно частот-
ному критерию устойчивости линейных систем
(см. §
11.3),
что
частотная характеристика линейной части ситемы
W(jca)
охва-
тывает точку
(—~7ТГ~Т
»
/0)
в
положительном направлении
\
к
(0) /
s
H
/2
раз, где
s
H
—индекс
неустойчивости
(рис.
17.14).
Проведем
Рис.
17.13.
Рис.
17.14.
на
плоскости
W
окружность достаточно малого радиуса
8
с цен-
тром
в
точке
(
—
——-,
/0
]
так,
чтобы
она не
пересекалась
с
W(jco).
Эта
окружность представляет собой
не что
иное,
как
&0)8,
k№(0)—s)-окружность,
и она
определяет сектор
е,
&<
д
>(0)
—е),
которому принадлежит начальная часть
характеристики нелинейного элемента.
Всегда
можно выбрать
такое малое
r)
=
sup|/(0|
или
r\
=
sup
|
f^(t)
+
/J(/)|,
что х не
будет
выходить
за
пределы начальной части характеристики
Ф(л;),
принадлежащей сектору
(й
(д)
(0)—8,
fe(w(0)+e).
В
этом
случае
выполняются условия кругового частотного критерия
(критерий
IV), но при
малых отклонениях
х от
нуля. Отсюда
мы
приходим
к
выводу,
что
I
нелинейная
система
будет
устойчива
«в
малом»,
если
со-
ответствующая
ей
линеаризованная
система
устойчива.
Устойчивость
«в
малом» лишь констатирует факт устойчивости,
но
не
определяет каких-либо границ области устойчивости.
Уве-
личим
s
до
величины, при которой
(&
(д)
(0)
+Б,
&
(д)
(0)
—
е)-окруж-
ность касается частотной характеристики линейной
ч^рти
(рис.
17.14).
При
этом раствор сектора
(&
д
)(0)—е,
&<
д
)(0)+в)
увеличится
до
максимально возможного
при
заданном
£
(
д)
(0).

ЗАДАЧИ 285
Характеристика Ф(х) нелинейного элемента принадлежит сек-
тору
(#
д
)(0)
—
8,
kW(0)-{-e)
для ограниченных значений х, а вне
некоторого отрезка она выходит за пределы сектора. Если вели-
чину
Y]
=
sup|/(/)|
или
ц
=
sup
|
f^
(t) +
f^
(/)
| ограничить так,
чтобы х удовлетворяло неравенству
\х\^.
const, то нелинейная
система
будет
устойчива «в большом». Легко установить анало-
гичным путем факт устойчивости «в малом» и «в большом» при
других
способах линеаризации. Применению частотных крите-
риев абсолютной устойчивости состояния равновесия и процес-
сов для исследования устойчивости конкретных систем и устано-
вления
закономерностей, связанных с абсолютной устойчивостью,
посвящена
следующая глава.
Задачи
17.1.
Использовать результаты задачи 15.5 для установления кругового
критерия
абсолютной устойчивости.
17.2. Показать, что геометрическая интерпретация условия устойчивости
при
(?^0и^>г^0
состоит в том, что частотная характеристика
W(/со)
линейной части
системы
должна располагаться при со ^ 0 вне окружности с центром в точке
1/1
М
. 1 . / 1 1
пересекающей действительную ось в
точках
,
г-.
17.3. Показать, что q = 0 в задаче 17.2
соответствует
обычному круго-
вому критерию абсолютной устойчивости.

Глава
IS
ИССЛЕДОВАНИЕ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ
НЕЛИНЕЙНЫХ
АВТОМАТИЧЕСКИХ СИСТЕМ
§
18.1. Абсолютная устойчивость состояния равновесия
типовых систем
Исследование абсолютной устойчивости состояния равнове-
сия
нелинейной автоматической системы основано на примене-
нии
линеарного или параболического критериев, в которых фи-
гурирует
модифицированная частотная характеристика
W
M
(/со)
=
U
M
(со) +
/V
M
Н
=
U
(со) +
hV
(со).
Напомним,
что
£/(со)
и V(co) представляют собой действитель-
ную и мнимую части обычной частотной характеристики линей-
ной
части
W(j(o).
Значения
WV(/co)
и
W(jco)
совпадают при
со
= 1 и на действительной оси, где
V(to)
= 0
(рис.
18.1, а). При
со = оо значения
W
M
(j®)
и
W(/to)
также совпадают, если сте-
пень
г
передаточной функции
W(p)
больше единицы, т.е.
г
=
=
п — т
>
1. Если же
г
= п
—
т — 1, то
V
M
(оо) =
lim
coV
(со)
=
а < О
(0->оо
и,
следовательно, значение модифицированной частотной харак-
теристики
W
M
(j(&)
при со = оо
будет
расположено не в начале
координат, а на отрицательной мнимой оси (рис.
18.1,6).
Отме-
ченные свойства позволяют, с одной стороны, легко построить
№
м
(/<*>)
по
W(jca),
а с
другой
стороны, выяснить возможности,
когда об абсолютной устойчивости состояния равновесия нели-
нейной
системы можно судить непосредственно по частотной ха-
рактеристике
W(/co)
линейной части системы.
Если
модифицированная частотная характеристика
И^м(/со)
построена, то, применяя линеарный или параболический крите-
рий,
нетрудно определить границы изменения статического
коэф-
фициента
усиления нелинейного элемента
k^(x)
y
при котором
обеспечивается абсолютная устойчивость состояния равновесия
нелинейной
системы. Наибольшая верхняя граница достигается
§
18.1]
АБСОЛЮТНАЯ
УСТОЙЧИВОСТЬ
СОСТОЯНИЯ РАВНОВЕСИЯ
2В7
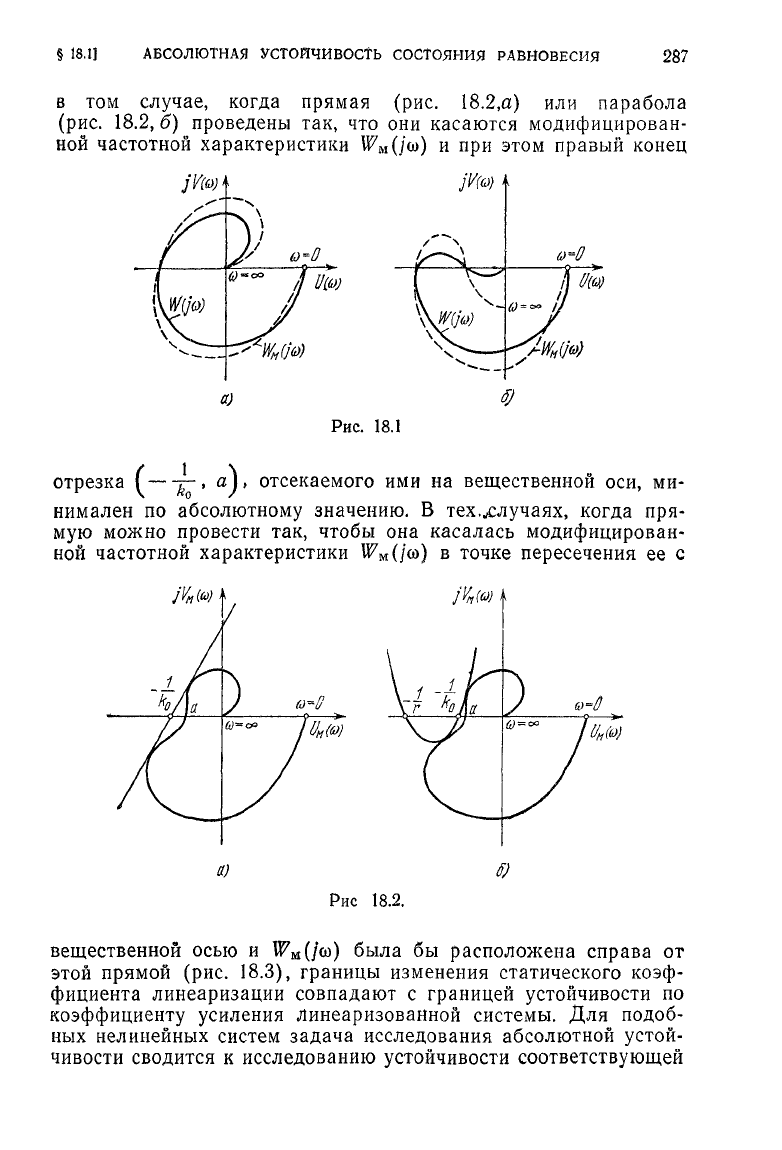
в
том случае, когда прямая (рис.
18.2,а)
или парабола
(рис.
18.2,6)
проведены так, что они касаются модифицирован-
ной
частотной характеристики
W
M
(joy)
и при этом правый конец
f
\
\\
V
jV(Q)
.
\
\
^
/1
(/(Я
/
У
Рис.
18.1
отрезка
Г
—
-т-,
а\,
отсекаемого ими на вещественной оси,
ми-
нимален
по абсолютному значению. В
тех.^лучаях,
когда
пря-
мую можно провести так, чтобы она касалась
модифицирован-
ной
частотной характеристики
ИР
м
(/со)
в точке пересечения ее с
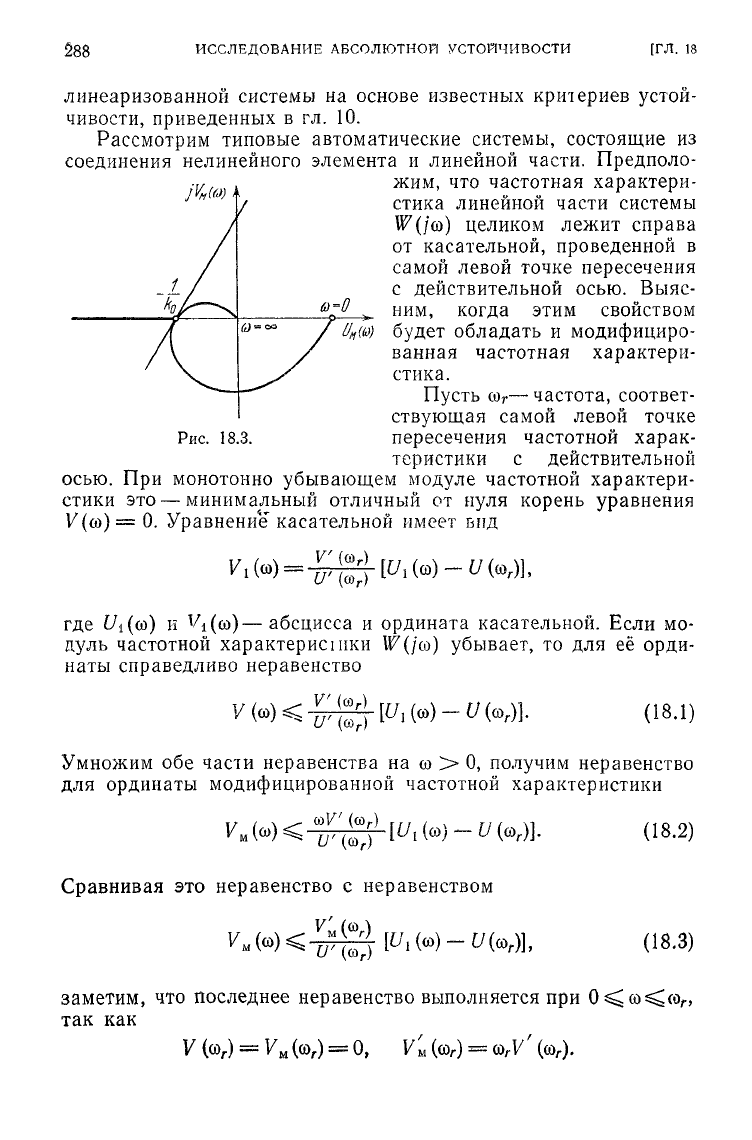
Рис
18.2.
вещественной осью и
lF
M
(/co)
была бы расположена справа от
этой
прямой (рис. 18.3), границы изменения статического
коэф-
фициента
линеаризации совпадают с границей устойчивости по
коэффициенту
усиления Линеаризованной системы. Для подоб-
ных нелинейных систем задача исследования абсолютной устой-
чивости сводится к исследованию устойчивости соответствующей
ИССЛЕДОВАНИЕ
АБСОЛЮТНОЙ
УСТОЙЧИВОСТИ
[ГЛ. 18
jV
M
(o)
>
линеаризованной
системы на основе известных критериев
устой-
чивости, приведенных в гл. 10.
Рассмотрим типовые автоматические системы, состоящие из
соединения
нелинейного элемента и линейной части. Предполо-
жим,
что частотная характери-
стика линейной части системы
W(j&)
целиком лежит справа
от касательной, проведенной в
самой левой точке пересечения
с действительной осью. Выяс-
ним,
когда этим свойством
будет
обладать и модифициро-
ванная
частотная характери-
стика.
Пусть
со
г
—
частота, соответ-
ствующая самой левой точке
Рис.
18.3. пересечения частотной харак-
теристики с действительной
осью. При монотонно убывающем
модуле
частотной характери-
стики
это
— минимальный отличный от нуля корень уравнения
У(со)
=
0.
Уравнений
касательной имеет вид
где
f/i
(со) и
^i(co)—абсцисса
и ордината касательной. Если
мо-
дуль
частотной
характерисшки
Щ/со)
убывает, то для её орди-
наты справедливо неравенство
-ш
(18.1)
Умножим обе части неравенства на со
>
О, получим неравенство
для ординаты модифицированной частотной характеристики
Ум(*>)<
°гГ^г[^1И-^/(со
г
)].
(18.2)
Сравнивая
это неравенство с неравенством
(18.3)
заметим, что последнее неравенство выполняется при
так как
V
(©,)
=
V
u
(co
r
)
=
0,
V'u
Ы
=
с»У
(со
г
).

§ 18.1]
АБСОЛЮТНАЯ УСТОЙЧИВОСТЬ СОСТОЯНИЯ РАВНОВЕСИЯ
289
Кроме
того, для выполнения (18.2) при со =
со
г
необходимо вы-
полнение
(18.1). Если действительная часть частотной характе-
ристики
принимает в точке
со
г
минимальное значение, то этого
достаточно для выполнения неравенства (18.3). Следовательно,
если
модуль
частотной
характеристики
системы
убывает
с
ростом
со, то
модифицированная
характеристика
будет
лежать
справа
от
касательной,
проведенной
в
самой
левой
точке
пересечения
ее с
действительной
осью.
В
этом
слу-
чае об
абсолютной
устойчивости
нелинейной
системы
мож-
но
судить
по
устойчивости
линеаризованной
системы.
Предположим, что передаточная функция линейной части си-
стемы имеет вид
1
(18.4)
где Q (р) — многочлен
п-и
степени, корни которого все веществен-
ны
и отрицательны. Один из нулей многочлена Q (р) может быть
равен нулю. Степень этой передаточной функции равна порядку,
т. е. п, а индексы неустойчивости, неминимально-фазовости и ко-
лебательности равны нулю. Полагая в (18.4) р = /со, находим
частотную характеристику линейной части:
Q-I
arg
Q
(/fi))
e
При
возрастании со от 0 до оо модуль частотной характеристики
и
ее фаза монотонно убывают. В этом случае границы измене-
ния
статического коэффициента линеаризации, обеспечивающие
абсолютную устойчивость состояния равновесия, совпадают с
предельными.
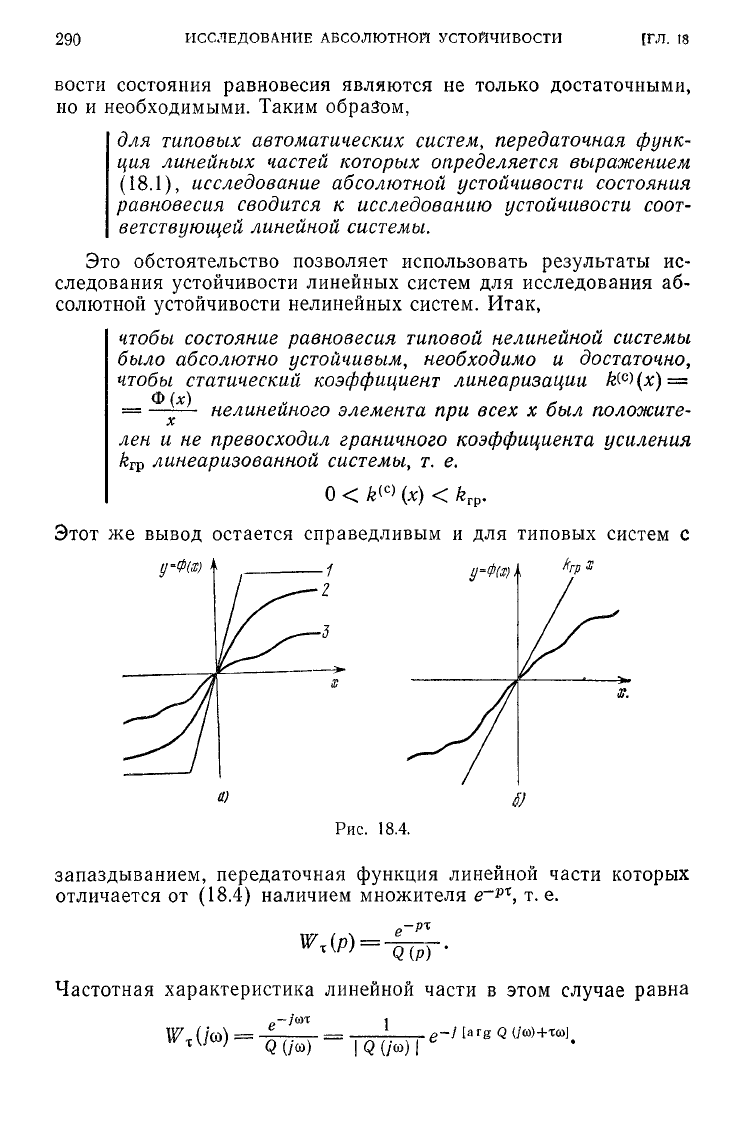
Для
системы
второго
порядка
абсолютная
устойчивость
состояния
равновесия
будет
иметь
место
при
любой
одно-
значной
характеристике
нелинейного
элемента,
располо-
женной
в
первом
и
третьем
квадрантах (рис. 18.4, а), а
для
систем
выше
второго
порядка
абсолютная
устойчи-
вость
состояния
равновесия
будет
иметь
место,
когда
ха-
рактеристика
нелинейного
элемента
будет
однозначна
и
расположена
в
секторе
(О,
k
TV
)
(рис.
18.4,6),
где
&
гр
—
граничный
коэффициент
усиления
соответствующей
ли-
нейной
системы.
Эти выводы остаются справедливыми и для характеристик
нелинейного
элемента, обладающих отрицательным гистерези-
сом.
Заметим, что в этих случаях условия абсолютной
устойчи-
Ю
Я. 3 Цыпкин
290
ИССЛЕДОВАНИЕ
АБСОЛЮТНОЙ
УСТОЙЧИВОСТИ
[ГЛ.
18
вости
состояния
равновесия
являются
не
только
достаточными,
но
и
необходимыми.
Таким
образом,
для
типовых
автоматических
систем,
передаточная функ-
ция
линейных частей которых определяется выражением
(18.1),
исследование абсолютной устойчивости состояния
равновесия сводится к исследованию устойчивости соот-
ветствующей
линейной системы.
Это
обстоятельство
позволяет
использовать
результаты ис-
следования
устойчивости
линейных
систем
для
исследования
аб-
солютной
устойчивости
нелинейных
систем.
Итак,
чтобы состояние равновесия типовой нелинейной системы
было
абсолютно
устойчивым,
необходимо и достаточно,
чтобы
статический
коэффициент линеаризации
kW(x)
=
=
——^
нелинейного
элемента при всех х был
положите-
лен
и не превосходил граничного коэффициента усиления
й
гр
линеаризованной системы, т.
е.
О
<
/г<
с)
(*)
< k
гр-
Этот
же вывод
остается
справедливым
и для
типовых
систем
с
у-ФШ
а)
Рис.
18.4.
запаздыванием,
передаточная
функция
линейной
части
которых
отличается
от (18.4)
наличием
множителя
е~
рх
,
т. е.
Частотная
характеристика
линейной
части
в
этом
случае
равна
ттг/
/;._\ с
1
/>-/
[arg
Q
(/(0)+Т(0]

§
18.2]
ПОЛОЖИТЕЛЬНЫЕ
КОЭФФИЦИЕНТЫ ЛИНЕАРИЗАЦИИ
291
Ее
модуль
и фаза монотонно
убывают
при возрастании
о)
от 0 до
оо.
В общем же
случае
линеарный критерий абсолютной устой-
чивости состояния равновесия является лишь достаточным.
Пример.
Рассмотрим систему, передаточная функция линейной части ко-
торой
равна
1
Р\
W
{)
Модифицированная
частотная характеристика
16
(со
2
—16,45)
W
u
(/со)
-
(1
+ со
2
)
[(16
-
со
2
)
2
+
(0,45со)
2
]
16
(1,45со
2
— 16)
j
(1 +со
2
)
[(16
—
со
2
)
2
+
(0
}
45со)
2
]
построена
на рис. 18.5. Граничный коэффициент усиления линеаризованной си-
стемы равен
1
и
"Тр,
Л
гл
о
Проводя
прямую, касательную к модифициро-
ванной
частотной характеристике, находим на
основании
линеарного критерия граничное зна-
чение
для статического коэффициента линеа-
ризации:
~
гр
0,77
""*
Положение
равновесия нелинейной системы
будет
абсолютно устойчивым, если
с)
(х)
=-
~
1,3.
Рис.
18.5.
Отсюда видно, что в рассматриваемом случае область устойчивости нелиней-
ной
системы меньше области устойчивости соответствующей линейной си-
стемы.
§
18.2. Абсолютная устойчивость состояния равновесия
при
любых
положительных коэффициентах
статической линеаризации
Выше было показано, что нелинейные системы второго по-
рядка
обладают
абсолютно устойчивым положением равновесия
при
любой однозначной характеристике нелинейного элемента,
расположенной в первом и
третьем
квадрантах. Типовые нели-
нейные системы
третьего
и более высокого порядка
всегда
имеют
конечный
граничный коэффициент усиления, определяющий пре-
делы
изменения статического коэффициента усиления нелиней-
ного элемента. Выделим классы нелинейных систем, в которых
