Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

272

УСТОЙЧИВОСТЬ НЕЛИНЕЙНЫХ СИСТЕМ

[ГЛ.

Учитывая, что е может быть сколь угодно малым положитель-

ным

числом, неравенство

(17.59)

можно записать в виде стро-

гого неравенства

q>0,

(17.60)

которое и является частотным критерием абсолютной устойчиво-

сти.

В него

входит

частотная характеристика линейной части си-

стемы

(/со), граничное значение

сектора

[0,

которому

принадлежит семейство нелинейных характеристик

Ф(х),

не-

отрицательное вещественное число д.

Для того чтобы показать, что частотное неравенство, при вы-

полнении

которого обеспечивается абсолютная устойчивость со-

стояния

равновесия нелинейной автоматической системы, спра-

ведливо и для q

0, преобразуем тождественно

схему

нелиней-

ной

автоматической системы на рис. 17.1. Введем обратное

соединение линейной части с усилительным элементом,

коэффи-

циент

усиления которого равен

и параллельное соединение

Ф(Т)

..*

Г"

Рис 17.3.

wit)

W(p)

ко

lit)

l(P)

нелинейного

элемента с таким же усилительным элементом, а за-

тем изменим знак у

выхода

нелинейного элемента и

входа

об-

ратного соединения (рис. 17.3). При этом, как легко видеть,

(17.61)

nv/—

+k()W{p)

•

Характеристика преобразованного нелинейного элемента и пере-

даточная функция преобразованной линейной части

будут

равны

соответственно

(

)

—

Ф (х)

(17.62)

l+k

W(p)

(17.63)

Поскольку

эквивалентные преобразования не изменяют свойства

системы, то если была абсолютно устойчива исходная нелиней-

Т7.3]

ЧАСТОТНЫЕ НЕРАВЕНСТВА

273

ная

система, преобразованная нелинейная система также

будет

абсолютно устойчивой. Так как

то из неравенства

следует

неравенство

^ х ^

и>

т.е.

характеристика преобразованного нелинейного элемента

принадлежит тому же сектору, что и характеристика исходного

нелинейного

элемента. Применим частотное неравенство

(17.59)

преобразованной нелинейной системе. Частотная характери-

стика линейной части преобразованной системы находится из

(17.63)

при р = /со:

(/со)

Поэтому частотное условие устойчивости состояния равновесия

преобразованной системы примет вид

Re(l +

qfa)

(/со) +

™-

> 0,

^>0.

(17.64)

Подставляя в

левую

часть неравенства выражение для

(/co),

после простых преобразований получим

Так

как первый из множителей положителен, то частотное нера-

венство

(17.64)

будет

выполняться одновременно с неравенством

Re (1 -

qja)

W (/со)

--- > 0, q

(17.65)

Таким

образом, из частотного условия устойчивости состояния

равновесия преобразованной системы

(17.64)

мы получили ча-

стотное условие устойчивости состояния равновесия исходной си-

стемы (17.65), в которое, в отличие от (17.64),

входит

параметр

q с обратным знаком. Но так как эквивалентное преобразование

исходной нелинейной системы не изменяет абсолютной устойчи-

вости, то из

(17.65)

следует,

что для однозначных характе-

ристик

нелинейных элементов в частотном неравенстве

(17.60)

274

УСТОЙЧИВОСТЬ

НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 17

параметр q может принимать любые вещественные значения, т. е.

—оо

< q < оо.

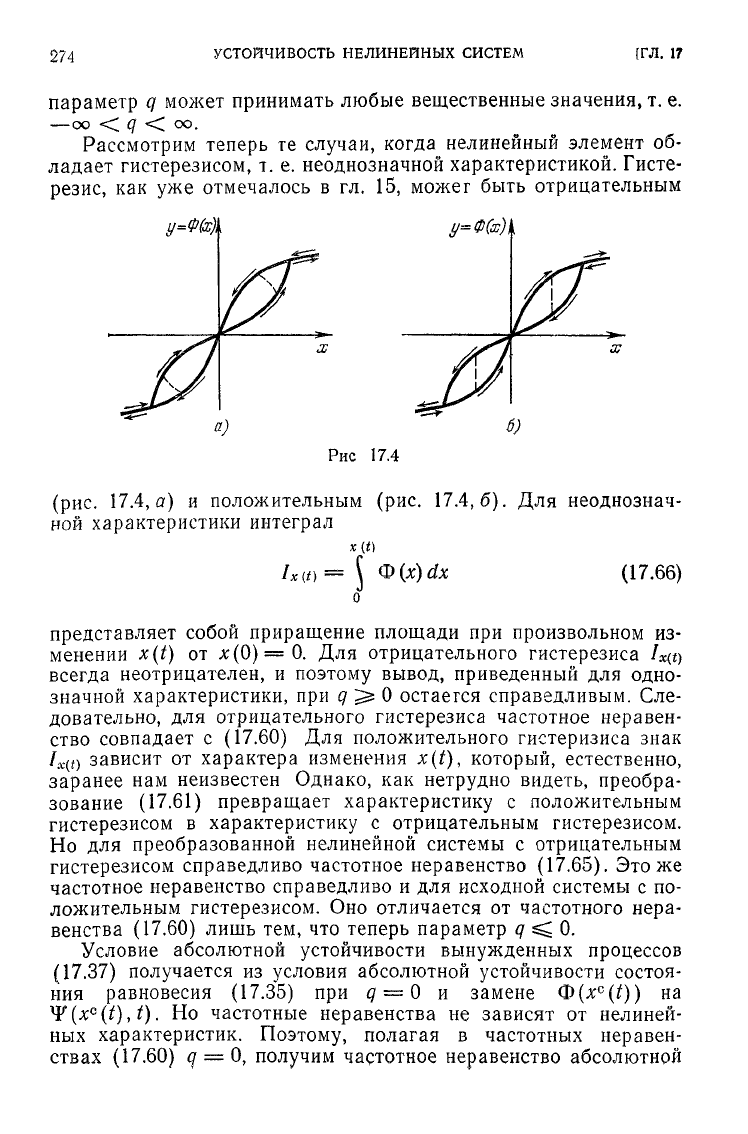
Рассмотрим теперь те случаи, когда нелинейный элемент об-

ладает гистерезисом, т.

е,

неоднозначной характеристикой. Гисте-

резис,

как уже отмечалось в гл. 15,

можег

быть отрицательным

Рис

17.4

(рис.

17.4,

а)

и положительным (рис.

17.4,6).

Для неоднознач-

ной

характеристики интеграл

x(t)

/*<*>

Ф{х)с1х

(17.66)

представляет собой приращение площади при произвольном из-

менении

x(t) от

х(0)=0.

Для отрицательного гистерезиса

(t)

всегда неотрицателен, и поэтому вывод, приведенный для одно-

значной

характеристики, при q ^ 0 остается справедливым. Сле-

довательно, для отрицательного гистерезиса частотное неравен-

ство совпадает с

(17.60)

Для положительного гистеризиса знак

ц)

зависит от характера изменения

x(t),

который, естественно,

заранее нам неизвестен Однако, как нетрудно видеть, преобра-

зование

(17.61)

превращает характеристику с положительным

гистерезисом в характеристику с отрицательным гистерезисом.

Но

для преобразованной нелинейной системы с отрицательным

гистерезисом справедливо частотное неравенство (17.65). Это же

частотное неравенство справедливо и для исходной системы с по-

ложительным гистерезисом. Оно отличается от частотного нера-

венства

(17.60)

лишь тем, что теперь параметр q ^ 0.

Условие абсолютной устойчивости вынужденных процессов

(17.37)

получается из условия абсолютной устойчивости состоя-

ния

равновесия

(17.35)

при

0 и замене

Ф(х

(/))

на

4(x

(t),t).

Но частотные неравенства не зависят от нелиней-

ных характеристик. Поэтому, полагая в частотных неравен-

ствах

(17.60)

</—

0, получим частотное неравенство абсолютной

17 4] КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ 275

устойчивости вынужденных процессов:

(/со)

т-

(17.67)

Отметим, что это же частотное неравенство обеспечивает абсо-

лютную устойчивость состояния равновесия нелинейной системы

нестационарной характеристикой нелинейного элемента вида

Ф(х

(1),

t).

(17.68)

17.4. Критерий абсолютной устойчивости

состояния

равновесия

Критерий

абсолютной устойчивости состояния равновесия не-

линейной

системы представляет собой геометрическую интерпре-

тацию частотного неравенства

причем

для однозначной стационарной характеристики нелиней-

ного

элемента

—

оо<<7<оо,

(17.69)

для неоднозначной характеристики с отрицательным гистере-

зисом

0<?<оо,

(17.690

для неоднозначной характеристики с положительным гисте-

резисом

-оо<<7<0,

(17.69")

для нестационарной однозначной и неоднозначной характе-

ристики

(17.69'")

Представим частотную характеристику линейной части в виде

(/со) =

£/(©)

+ /У (со).

(17.70)

Тогда, после подстановки

W(/со)

в частотное неравенство и вы-

деления

действительной части, получаем

£/(©)-<7<оУ(©)

+J->0.

(17.71)

«о

Введем понятие

модифицированной

частотной характеристи-

ки

линейной части:

й^м

(/со) =

(ш)

(со),

(17.72)

где

(со)

U (со),

(со)

соК

(со). (17.73)

276

УСТОЙЧИВОСТЬ

НЕЛИНЕЙНЫХ СИСТЕМ

[ГЛ.

Модифицированная

частотная характеристика

№

(/(о)

отличает-

ся

от обычной

W(j(x>)

лишь изменением масштаба мнимой части

со раз (рис. 17.5). На

плоскост

и модифициро-

ванной

частотной харак-

теристики уравнение

(17.74)

определяет прямую, про-

ходящую через точку оси

абсцисс —

-г-

с наклоном

— (рис. 17.5). Для крат-

кости

будем называть эту

Рис.

17.5 прямую (q,

)

-прямой,

или

прямой

В. Попова.

Тогда, очевидно, частотное неравенство (17.60) или, что

экви-

валентно,

(17.71)

выполняется, если модифицированная частот-

ная

характеристика расположена справа от (q,

)

-прямой. Та-

ким

образом, критерий абсолютной устойчивости состояния рав-

новесия

нелинейной системы можно сформулировать в следую-

щей

форме.

Частотный

критерий I

(линеарный

критерий).

Состояние

равновесия

= 0

нелинейной

системы

устойчивой

ли-

нейной

частью

будет

абсолютно

устойчивым,

если

харак-

теристика

нелинейного

элемента

Ф(х)

принадлежит

сек-

тору

[0,

]

или, что то же,

если

коэффициент

статической

линеаризации

k^(x)

принадлежит

полосе

[0,

]

моди-

фицированная

частотная

характеристика

линейной

части

(jdy)

не

пересекает

(q,

)-прямую.

Область, определяющая выбор

зависит от нестационарно-

сти и свойств характеристики нелинейного элемента (17.69)—•

(17.69"').

Так, рис. 17.5 свидетельствует об абсолютной устойчи-

вости состояния равновесия нелинейных систем с устойчивой ли-

нейной

частью и однозначной характеристикой нелинейного эле-

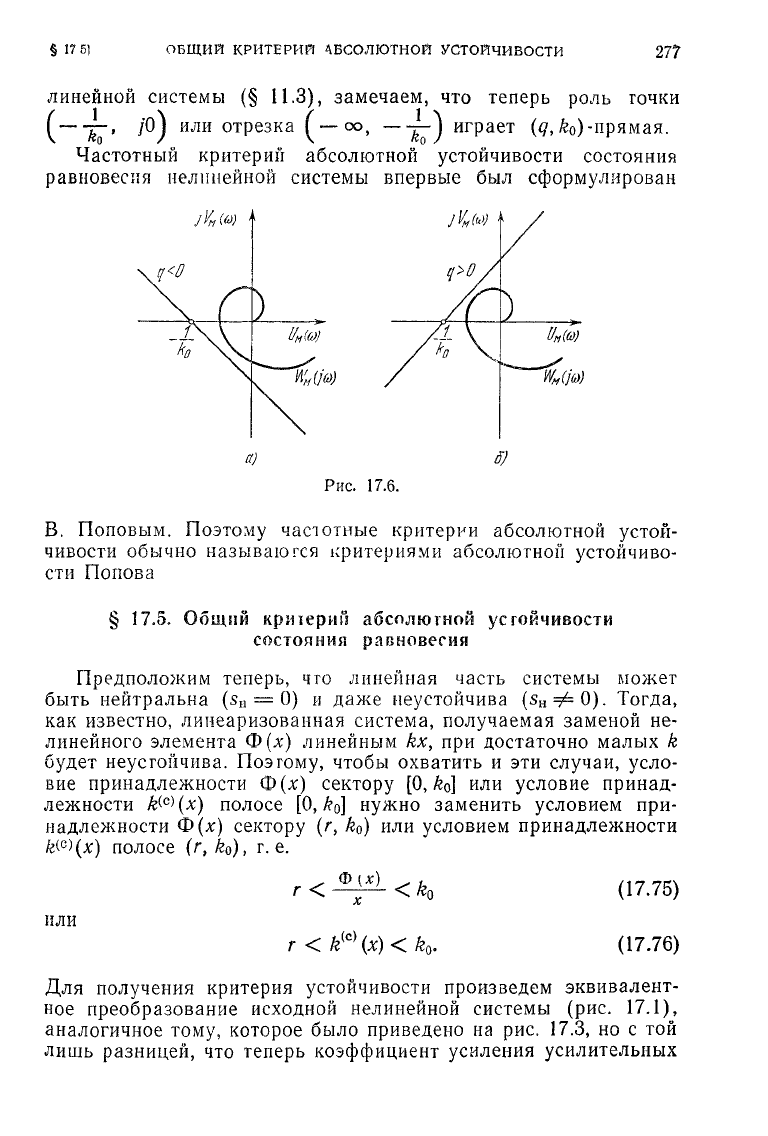
мента. Если же нелинейный элемент обладает гистерезисом, то

рис.

17.6, а соответствует абсолютной устойчивости состояния

равновесия при положительном гистерезисе, а рис.

17.6,6

— при

отрицательном гистерезисе. Сопоставляя эту формулировку ча-

стотного критерия абсолютной устойчивости состояния равнове-

сия

нелинейной системы с частотным критерием устойчивости

17 5]

ОБЩИЙ

КРИТЕРИЙ

АБСОЛЮТНОЙ УСТОЙЧИВОСТИ

27?

линейной

системы (§

11.3),

замечаем, что теперь роль точки

(•—

—»

/0J

или отрезка ^

—оо,

—

у]

играет

)-прямая.

Частотный критерий абсолютной устойчивости состояния

равновесия нелинейной системы впервые был сформулирован

Рис.

17.6.

В. Поповым. Поэтому частотные критерии абсолютной устой-

чивости обычно называются критериями абсолютной устойчиво-

сти Попова

17,5,

Общий

кршерий

абсолютной устойчивости

состояния

равновесия

Предположим теперь, что линейная часть системы может

быть нейтральна

= 0) и

даже

неустойчива

ф0).

Тогда,

как

известно, линеаризованная система, получаемая заменой не-

линейного

элемента Ф(х) линейным

кх,

при достаточно малых к

будет

неустойчива. Поэтому, чтобы охватить и эти случаи, усло-

вие принадлежности Ф(х) сектору [0,

]

или условие принад-

лежности

к^(х)

полосе [0,

]

нужно заменить условием при-

надлежности Ф(х) сектору

(г,

ко) или условием принадлежности

полосе

(/*,

ко), г. е.

r<~—

(17.75)

(17.76)

или

ic)

(х) <

Для получения критерия устойчивости произведем эквивалент-

ное

преобразование исходной нелинейной системы (рис. 17.1),

аналогичное

тому,

которое было приведено на

рис.

17.3, но с той

лишь

разницей, что теперь коэффициент усиления усилительных

278

УСТОЙЧИВОСТЬ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 17

элементов выберем равным не

и не

будем

менять знак

у выхода нелинейного элемента и

входа

обратного соединения.

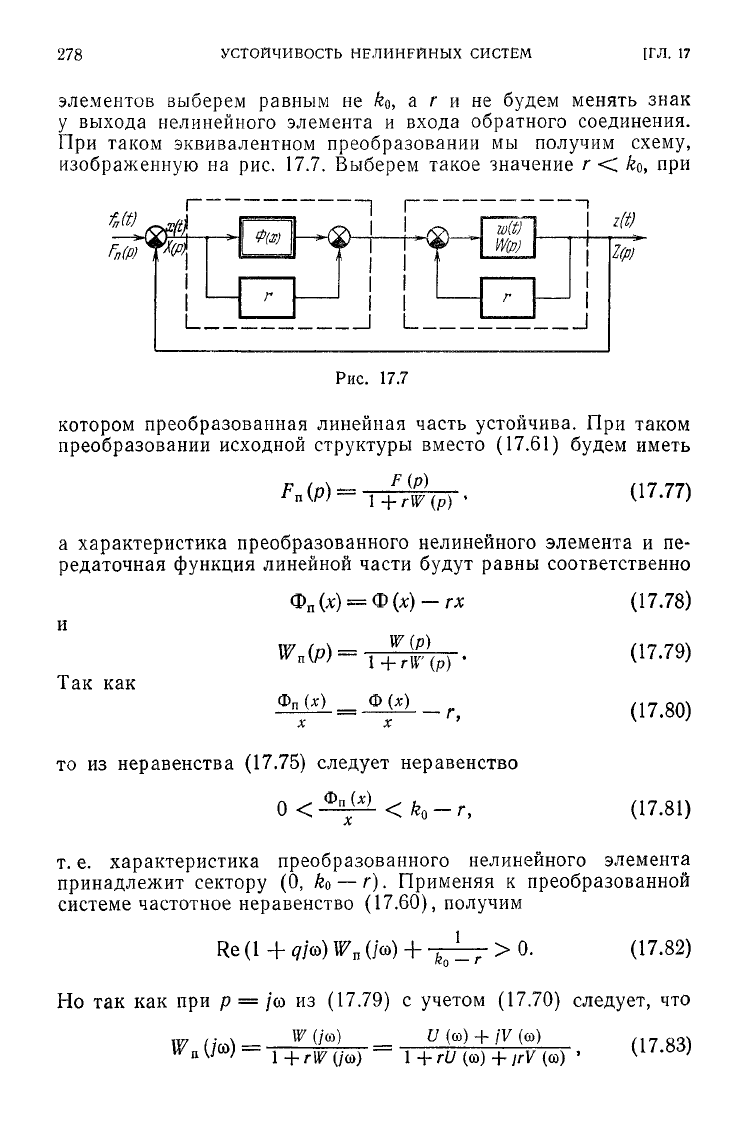
При

таком эквивалентном преобразовании мы получим

схему,

изображенную на рис. 17.7. Выберем такое значение

ko,

при

?vJL_

ft—*

—1

lit)

Zip/

Рис.

17.7

котором преобразованная линейная часть устойчива. При таком

преобразовании исходной структуры вместо

(17.61)

будем

иметь

F(P)

+rW(p)

(17.77)

а характеристика преобразованного нелинейного элемента и пе-

редаточная функция линейной части

будут

равны соответственно

(

)

(х) —

гх

(17.78)

(17.79)

(17.80)

Так

как

'—

l+rW(p)

•

Ф(*)

то

из

неравенства (17.75) следует неравенство

-^Ц-

—

г,

(17.81)

т. е. характеристика преобразованного нелинейного элемента

принадлежит сектору (0,

— r). Применяя к преобразованной

системе частотное неравенство (17.60), получим

). (17.82)

—r

Но

так как при р = /со из

(17.79)

с учетом

(17.70)

следует,

что

17/

(иЛ—

Г(/(0)

—

иЫ

!'У(®)

(\7№

rU ]rV

17.5]

ОБЩИЙ

КРИТЕРИЙ

АБСОЛЮТНОЙ УСТОЙЧИВОСТИ

то частотное неравенство (17.82) запишется в виде

279

(17.84)

После

простых преобразований и выделения действительной части

получаем

(со)

£)

U (со) ~

£)

q»V

(со) +

К»

(со)

-±г

> 0.

(17.85)

Но

уравнение

(17.86)

на

плоскости модифицированной частотной характеристики

(j(o)

определяет параболу,

проходящую через точки оси

абсцисс — —, ~~ _.

Каса-

тельные к параболе в точках

—

-г-

имеют

наклоны

1 1

— — и — и пересекаются в

точке а

(рис.

17.8). Будем на-

зывать эту параболу (q, ko, г)-

параболой. Выполнение частот-

ного неравенства соответствует

расположению модифициро-

ванной

частотной характери-

стики

линейной части

(jсо)

вне (q,

г)-параболы.

Таким

Рис.

17.8.

образом, критерий абсолютной

устойчивости состояния равновесия нелинейной системы можно

сформулировать в такой форме.

Частотный

критерий II

(параболический

критерий). Со-

стояние

равновесия

= О

нелинейной

системы

будет

аб-

солютно

устойчивым,

если

характеристика

нелинейного

элемента

Ф(х)

принадлежит

сектору

(г,

ko) или, что то

же,

если

коэффициент

статической

линеаризации

k^(x)

принадлежит

полосе

(г,

ko),

модифицированная

частот-

ная характеристика

линейной

части

(j(a)

не

пересекает

(q,

k)-параболы

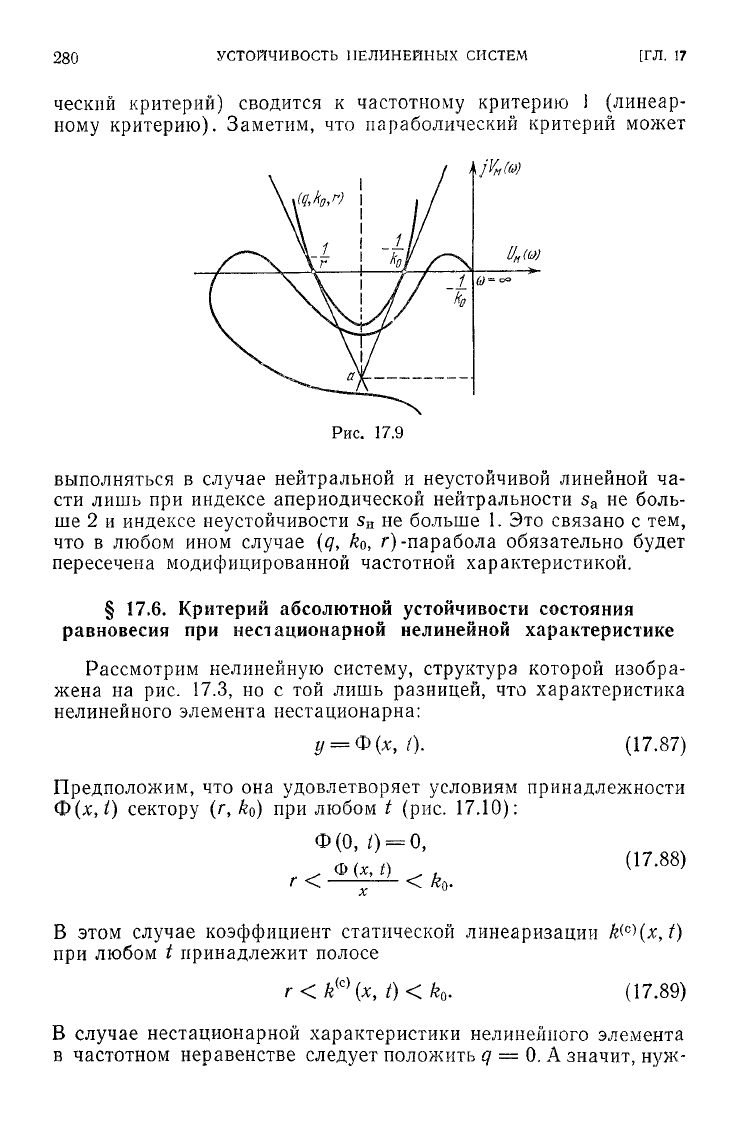
(рис. 17.9).

При

стремлении

к нулю

(q,

r)-парабола вырождается

(q,

ko)-прямую (рис. 17.6) и частотный критерий II (параболи-

1(1

280

УСТОЙЧИВОСТЬ

НЕЛИНЕЙНЫХ СИСТЕМ

[ГЛ. 17

ческий

критерий) сводится к частотному критерию 1 (линеар-

ному критерию). Заметим, что параболический критерий может

(6»

Рис.

17.9

выполняться

случае

нейтральной и неустойчивой линейной ча-

сти лишь при индексе апериодической нейтральности

не боль-

ше 2 и индексе неустойчивости

не больше 1. Это связано с тем,

что в любом ином

случае

(q,

r)-парабола обязательно

будет

пересечена модифицированной частотной характеристикой.

17,6. Критерий абсолютной устойчивости состояния

равновесия при

нес!ационарной

нелинейной характеристике

Рассмотрим нелинейную систему,

структура

которой изобра-

жена на рис. 17.3, но с той лишь разницей, что характеристика

нелинейного

элемента нестационарна:

у =

Ф(х,().

(17.87)

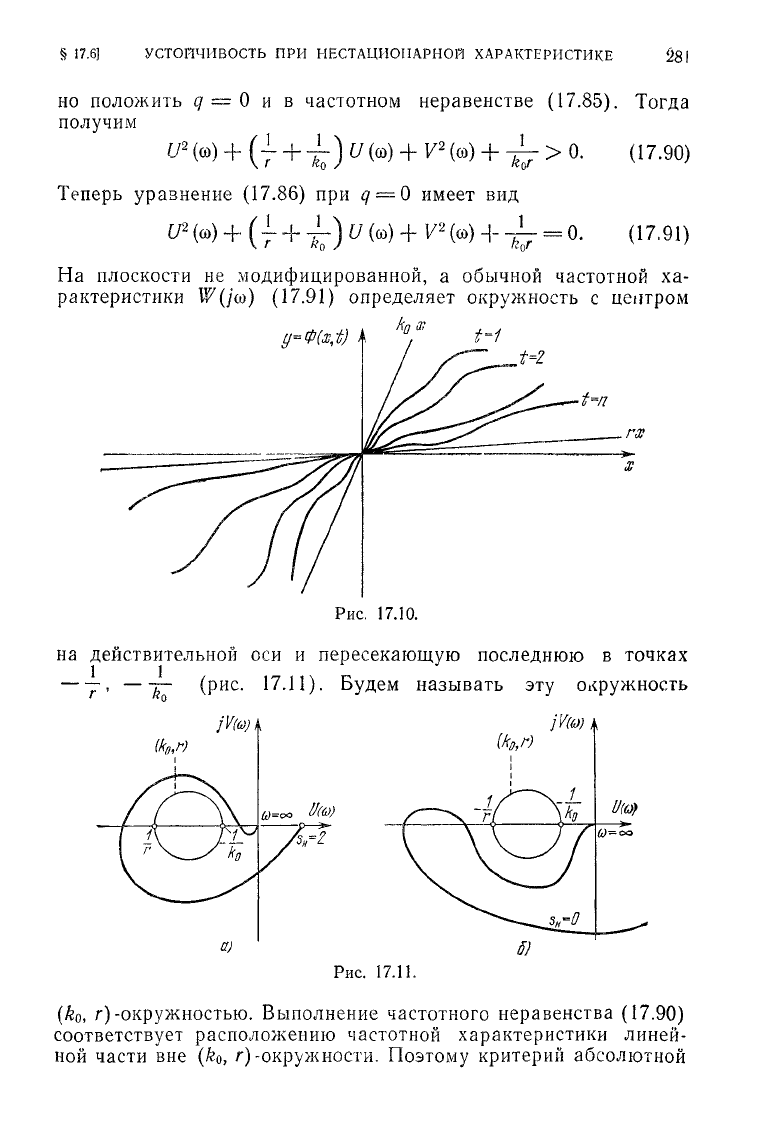
Предположим, что она удовлетворяет условиям принадлежности

Ф(х,

сектору (г,

ko)

при любом t (рис.

17.10):

г<

ф(о,

/)-

(*,

(17.88)

В этом

случае

коэффициент статической линеаризации

при

любом t принадлежит полосе

{c)

{х,

t) <

(17.89)

случае

нестационарной характеристики нелинейного элемента

частотном неравенстве

следует

положить q = 0. А значит, нуж-

17.6]

УСТОЙЧИВОСТЬ

ПРИ НЕСТАЦИОНАРНОЙ

ХАРАКТЕРИСТИКЕ

281

в частотном неравенстве (17.85). Тогда

(17.90)

Теперь уравнение (17.86) при q

имеет вид

(со) + V

(

)

= 0. (17.91)

но

положить

получим

— )

(со) + V

(со)

-±

> 0.

На

плоскости не модифицированной, а обычной частотной ха-

рактеристики

W(jw)

(17.91) определяет окружность с центром

д-ФШ)

Рис.

17.10.

на

действительной оси и пересекающую последнюю в точках

—

у,

—у

(рис.

17.11). Будем называть эту окружность

jV(v)

U(Q)

Рис.

17.11.

(&о,

г)-окружностью.

Выполнение частотного неравенства

(17.90)

соответствует расположению частотной характеристики линей-

ной

части вне

(ко,

г)-окружности.

Поэтому критерий абсолютной