Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

242 УРАВНЕНИЯ

ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ СИСТЕМ

[ГЛ. 15

и,

следовательно,

2п

г)

(А)

{T)

(А)

{

]

(А)

(Л sin

ш/)

sin

со/

darf.

(15.23)

В этом случае гармонический коэффициент линеаризации веще-

ственный.

И,

значит,

kT{A)t{t\

(15.24)

Нетрудно видеть,

что

{А)

kf'(А)

представляют собой

отношение

коэффициентов первой гармоники разложения

в ряд

Фурье периодической функции (15.11)

амплитуде входного

пе-

риодического воздействия.

Уравнения

гармонической

линеаризации (15.20), (15.24)

представляют

собой

аппроксимацию

уравнения

нелиней-

ного

элемента

(15Л1)

при

гармоническом

воздействии.

Предположим теперь,

что

x(t)—стационарный

случайный

процесс,

тогда

y(t) =

<S)(x(t))

будет

также стационарным

слу-

чайным

процессом. Определим

коэффициент

стохастической

ли-

неаризации

ст

)

из

условия наилучшего среднеквадратического

приближения

y(t)

величиной

№*x(t),

(15.25)

т.

е. из

условия

M{[y(t)-p(t)]

}->mm,

(15.26)

fc(CT)

или,

развернутой форме,

М {[Ф (х (0)

k'^x

(t)]

}

min.

(15.27)

(CT)

Дифференцируя левую часть (15.27)

по

(CT)

приравнивая

ее

нулю, получим

М {[Ф (х (0)

(

^'x

(/)]

(/)}

(15.28)

Отсюда, учитывая,

что

оо

М {Ф (х (0)

(/)}

«=

(0)

Ф (х)

хр

(х)

dx,

(15.29)

15.4]

ЛИНЕРЙЗАЦИЯ

НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ 243

где

(0)

{0)

— начальные значения взаимной и собствен-

ной

корреляционной функции, получаем выражение для

коэф-

фициента

стохастической линеаризации:

оо

Поскольку

для стационарных эргодических процессов

(0)

#*(())

можно также представить в виде

(15-31)

-т

то,

наряду с (15.30), коэффициент стохастической линеаризации

можно определить и так:

&ст

^(ст

(

ах

)

\(b(x(t))x(t)at.

(15.32)

Уравнение

стохастической

линеаризации (15.25)

предста-

вляет

собой

аппроксимацию

уравнения

нелинейного

эле-

мента

при

случайном

воздействии.

В частном случае, если

x{f)

= A sin (со/ + Ф), (15.33)

где

— случайная фаза, из (15.31) следует

Ryx

(0)

lim

\ф{А sin (о/ + ф)) A sin (со/ + ф) dt

(Л)

с£

(15.35)

и,

значит,

(СТ)

Г)

И),

(15.36)

т. е. коэффициенты стохастической и гармонической линеариза-

ции

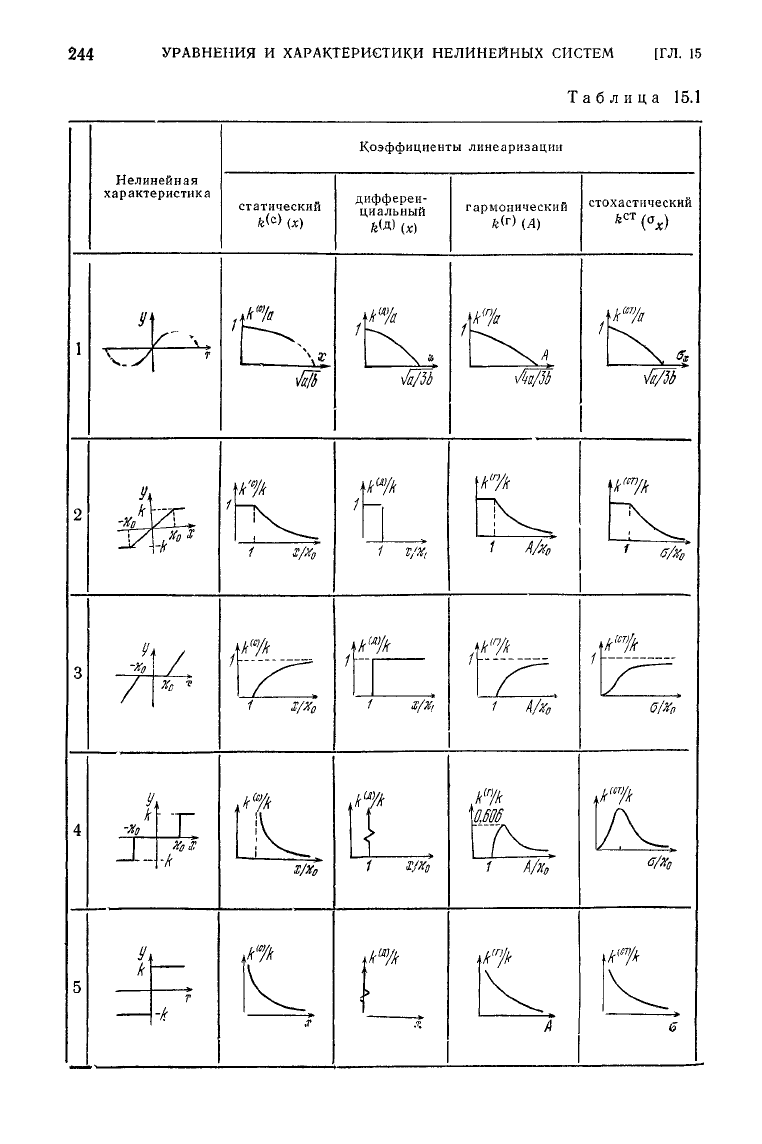
в этом случае совпадают. В табл. 15.1 приведены типовые

244

УРАВНЕНИЯ И ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ СИСТЕМ [ГЛ. 15

Таблица

15.1

Нелинейная

характеристика

•

!К

\.У\

-Хо

Коэффициенты

линеаризации

статический

fete)

(JC)

Х/Х

1 Х/Но

Л/Ко

f'/k

дифферен-

циальный

£<Д)

(х)

•к'%

">/к

т/х

(

м/

Х/Х,

/к

х/х,

гармонический

fete)

(A)

^й/ЗЬ

(п

/к

(П

/к

А/х.

(п

/к

А/х„

стохастический

•k

—^

в/К,

15.5]

УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ

245

характеристики

нелинейных элементов и соответствующие им

коэффициенты

статической, дифференциальной, гармонической и

стохастической линеаризации, которые удобно использовать при

исследовании нелинейных систем.

15.5. Уравнения нелинейных систем

Блок-схема простейшей нелинейной системы, к которой путем

структурных преобразований может быть сведена любая систе-

ма, содержащая один нелинейный элемент, изображена на

рис.

15.17.

Здесь предполагается, что внешнее воздействие f(t)

приложено ко

входу

нелинейного элемента. Уравнение нелиней-

ного элемента примем в виде (15.1), т. е.

y(t)

O(x(Q)

(15.37)

или

относительно изображений

оо

Y(p)

L {Ф (х (t))}

\ф(х

(0)

е-*

dt.

(15.38)

Уравнение же линейной части относительно изображений

имеет вид

где

Q (Р)

(15.39)

(15.40)

Рис.

15.17,

— передаточная функция линейной части. Условие замыкания

системы имеет вид

x{t) =

f(t)-z(£)

(15.41)

или

относительно изображений

F(p)-Z(p).

(15.42)

Заменяя

(15.39)

Y(p) его значением из

(15.38)

и учитывая

условие замыкания (15.42), получаем уравнение нелинейной си-

стемы в изображениях относительно выходной величины:

Z{p)

(p) L

{Ф(/(0

-z

(/))}.

(15.43)

Если

же в

(15.39)

заменить Y(p) его значением из

(15.38)

и под-

ставить значение Z(p) в

(15.42),

то мы получим уравнение не-

линейной

системы в изображениях относительно ошибки:

X(p)

F (p)

-W(p)L

{Ф (х (t))}. (15.44)

Это уравнение нелинейно, поскольку в него

входят

изображения

x(t)

и нелинейной функции

(*(*)).

Если перейти в

(15.44)

246 УРАВНЕНИЯ

ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ СИСТЕМ

[ГЛ 15

(15.43)

от изображений к оригиналам, а для этого достаточно

воспользоваться теоремой линейности и теоремой свертывания

(теоремы 1 и 6 приложения

1),

то мы получим уравнение в ори-

гиналах относительно выходной величины:

z(t)=\w(t-x)<D{f

(т) - z

{%))

dx,

(15.45)

относительно

ошибки:

х (t)

f {t) -

{t - т) Ф

(T))

dx. (15.46)

Интегральные уравнения

(15.45)

(15.46)

представляют собой

нелинейные

интегральные уравнения. К сожалению, не суще-

ствует

общих методов решения нелинейных уравнений (15.45)

или

(15.46). Однако, учитывая специфику нелинейных элементов

или

линейных частей, можно точно или приближенно исследо-

вать процессы в нелинейных системах. Разумеется, решения по-

добных нелинейных интегральных уравнений

могуг

быть полу-

чены различными численными или алгоритмическими методами

с помощью ЦВМ. Нас

будут

в основном интересовать та-

кие

методы исследования нелинейных систем, которые позволяют

установить их свойства и особенности, не находя непосред-

ственно решения описывающего их уравнения.

Рассматриваемые нелинейные автоматические системы пол-

ностью определяются заданием характеристики нелинейного эле-

мента и передаточной функцией или временной характеристикой

линейной

части системы. Если к нелинейной системе приложено

несколько

воздействий, например, кроме задающего воздействия

еще и возмущающие, то, как было показано ранее, все возму-

щающие воздействия

могут

быть приведены к точке приложения

задающего воздействия. При этом уравнения относительно ошиб-

ки

(15.44),

(15.46)

останутся без изменений, только F(p) и f(t)

будут

включать в свой состав изображения и оригиналы реак-

ций

линейной части системы на эти воздействия. Поэтому при

исследовании нелинейных систем мы ограничимся уравнением

ошибки

с одним приведенным воздействием f(t).

Задачи

15.1.

Показать, что для однозначных характеристик коэффициент

гармо-

нической

линеаризации веществен.

15.2. Показать, что при гауссовой плотности распределения

2о

р (х)

ЗАДАЧИ

247

а.

z(t)

»>

tit)

•*—

Рис.

15.18.

Рис.

15.19.

)

—

Г"

1 1

W(p)

l(p)

f—\

k~r

—

k-r

(P)

Рис

15.20.

248

УРАВНГНИЯ

ХАРАКТЕРИСТИКИ

НЕЛИНЕЙНЫХ

СИСТЕМ

ГГЛ

коэффициент

стохастической линеаризации

x<b(x)p(x)dx

коэффициент

дифференциальной линеаризации

/г

(д)

(х)

••

(х)

связаны

соотношением

Пользуясь этим соотношением, определить

>(а

)

по

№)(jf),

приведенному

табл.

15.1.

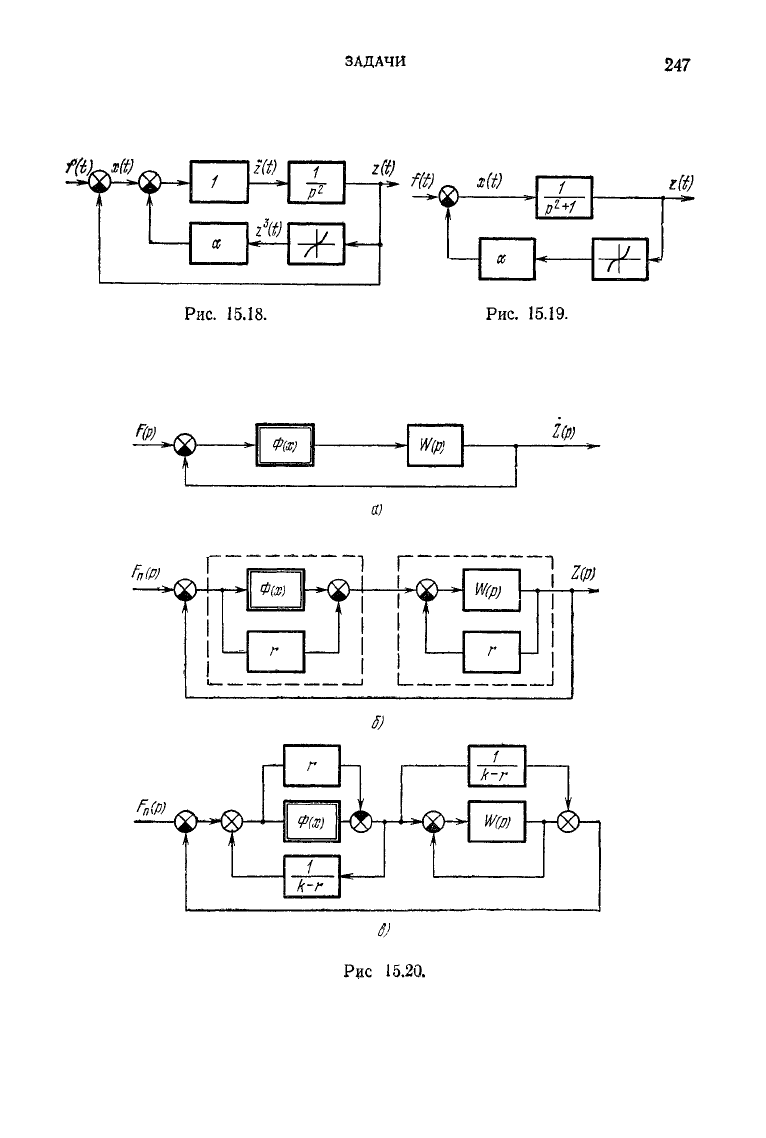
15.3. Показать,

что

уравнение Дюффинга

+ г +

аг

описывает нелинейную систему, структура которой имеет

вид,

изображенный

на

рис 15 18

или

на

рис.

15.19.

15.4. Убедиться

эквивалентности структур нелинейных систем, изобра-

женных

на рис

15 20,

а, б, в

15.5. Показать,

что

если

Ф(х)/х

<С

k для

структуры

на рис

20,6,

то эквивалентная характеристика нелинейного элемента принадлежит сектору

(0,

—

r),

а для

структуры, изображенной

на

рис.

15.20,

в,

— сектору

(0, оо).

лава

ПРОЦЕССЫ

НЕЛИНЕЙНЫХ

СИСТЕМАХ

16.1.

Вынужденные

свободные

процессы

Процессы

в нелинейных автоматических системах отличаются

от процессов в линейных системах весьма большим разнообра-

зием.

Несмотря на это, целесообразно для нелинейных систем

ввести понятия

вынужденного

свободного

процессов, которые

позволили бы выяснить свойства и особенности этих процессов,

а для линейных систем совпадали бы с известными аналогич-

ными

понятиями (см. § 8.3).

Уравнение нелинейной системы, полученное в предыдущей

главе, имеет вид

x(t)=

f(t)-\w(t

-%)Ф(х(*))<11.

(16.1)

Здесь предполагается, что внешнее воздействие приложено ко

входу

нелинейной автоматической системы в момент / = 0, а до

этого момента система находилась в покое. Для введения

поня-

тия

вынужденного

процесса

рассмотрим произвольное ограничен-

ное

неисчезающее внешнее воздействие

f(t)=

^(t)

и предполо-

жим,

что оно прикладывается ко

входу

нелинейной автоматиче-

ской

системы в некий произвольный момент времени t —

to.

Тогда

уравнение нелинейной системы вместо

(16.1)

прини-

мает

вид

(/)

At)

(t-

т)

Ф (x

(т))

dr.

(16.2)

В этом уравнении

— момент возмущения системы, a t — мо-

мент наблюдения процесса в ней. Под вынужденным процессом

(t)

естественно подразумевать процесс, вызванный внешним

ограниченным

воздействием, приложенным в момент времени

—со,

отстоящий от момента наблюдения на бесконечно

большой интервал времени. Полагая в

(16.2)

—~°°,

получим

250

ПРОЦЕССЫ В НЕЛИНЕЙНЫХ

СИСТЕМАХ

[ГЛ.

Т6

уравнение вынужденного процесса

(t)

(/)

w {t -

т)

(х

(т))

йт

(16.3)

—

оо

или,

после замены переменных в интеграле

(16.3)

/ —

на т

на

—т,

оо

х*

(/)

(т) Ф

{х

т))

dr.

(16.4)

Уравнения (16.3),

(16.4)

являются

уравнениями

вынужденного

процесса.

Под

свободным

процессом

(t)

естественно понимать раз-

ность

между

общим x(t) и вынужденным

(t)

процессами, т.е.

*(0-*

(0,

/>0.

(16.5)

Полагая в уравнении

(16.1)

f(t) =

(t) и вычитая из него урав-

нение

(16.3), получаем, после очевидных преобразований,

урав-

нение

свободного

процесса

h{t)-\w{t-

т)

[Ф

(х*

(т) +

(т))

(х

(г))]

dx.

(16.6)

Здесь функцию

оо

(^-т))^т,

(16.7)

как

нетрудно понять, можно рассматривать как причину, вызы-

вающую свободный процесс, которая связана с приложением

внешнего воздействия к нелинейной системе, находящейся до

момента его приложения в покое. Если же, кроме приложения

внешнего воздействия, в этот момент начальные значения коор-

динат состояния не нулевые, то в уравнения общего процесса

(16.1)

при

f(t)=f^(t)

и свободного процесса

(16.7)

следует

до-

бавить воздействие

f°(t),

представляющее собой реакцию линей-

ной

части системы на эти ненулевые начальные состояния.

Таким

образом, в общем

случае

при ненулевом начальном

состоянии

уравнения общего и свободного процессов

будут

иметь вид

(0 =

(0 +

/°*

(0 -

о»

т)

(х

(т))

(16.8)

(t)

(/)

flit)

\w(t

- x)

[Ф(x

(T)

(T))

Ф(x*(T))]

dx.

(16.9)

16.2] ПОНЯТИЯ СОСТОЯНИЙ РАВНОВЕСИЯ И АВТОКОЛЕБАНИЙ 251

Что же касается уравнений вынужденного процесса (16.3) или

(16.4), то они остаются без изменений. Вынужденные процессы

не

зависят от начального состояния системы. Как видно из

(16.9),

свободный

процесс

нелинейных

системах

существенно

зависит от

вынужденного

процесса

(t),

значит,

в ко-

нечном

итоге

и от

внешнего

воздействия

f^(t).

В общем случае при произвольной характеристике нелиней-

ного элемента невозможно аналитически решить уравнения

(16.4), (16.9) или (16.8) и, значит, невозхможно в явном виде

получить выражения вынужденного

(t),

свободного

(t)

полного x(t) процессов. В линейном случае, т. е. при

у =

ф(

)

х,

(16.10)

из

уравнений (16.4), (16.9) и (16.8) получаем

v{%)x*{t-%)dx

(16.11)

^(0

fl(t)-\w(t-

т)х

(т)dx

(16.12)

(16.13)

Эти уравнения сравнительно просто решаются, и их решения

совпадают с решениями, полученными иным путем для линей-

ных систем в гл. 8.

16.2.

Понятия

состояний

равновесия

автоколебаний

Если

в уравнении вынужденного процесса (16.4) положить

что соответствует устранению внешнего ограниченного воздей-

ствия,

то мы получим уравнение, определяющее

автономные

стационарные

состояния

(t)

нелинейной системы:

оо

(/)

(т) Ф

(х

- т))

dx.

(16.14)