Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

212

CHCTFMbI

ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ

[ГЛ

Для

стационарных

эргодических

процессов

статистические

характеристики,

полученные

усреднением

по

множеству

по

времени,

равны

друг

другу,

т. е.

и,

значит,

(x(t)

- x

(t)f

= (x (t) - x

(t)f

{[x

]

}

Эргодичность широкого класса стационарных случайных про-

цессов позволяет множество случайных процессов образовывать

из

отрезков конечной длины одной достаточно продолжительной

по

времени реализации случайного процеса. Поскольку далее мы

будем

иметь дело только с эргодическими случайными процесса-

ми,

для которых имеет место эквивалентность усреднения по

множеству и по времени, то введем общий символ усреднения

М{-},

под которым мы

будем

понимать удобный для нас вид

усреднения. Чаще из-за наглядности мы

будем

использовать

усреднение по времени.

Наиболее важной характеристикой случайного процесса яв-

ляется корреляционная функция, указывающая степень зависи-

мости между значениями случайного процесса в моменты време-

ни,

отстоящие

друг

от

друга

на величину т. Заменяя в формуле

для

(x)

/на

—

т, получим

т. е.

корреляционная

функция

является

четной

функцией

сдви-

га т. Для стационарного случайного процесса сдвиг на т в сто-

рону возрастания или убывания времени не меняет степени зави-

симости значений случайного процесса. При т = 0 получаем, что

Начальное значение корреляционной функции равно среднему

значению квадрата случайного процесса. Из выражения для дис-

персии

следует

также

Начальное значение корреляционной функции равно сумме

дис-

персии и квадрата среднего значения случайного процесса. Из

§14

ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ

213

очевидного неравенства

{(*(/)

-х(/

т))

следует

{х

(/)}

+ М {х

т)}

2М {х (0 х {t + т)}.

Так как

то

(0)

>/г

(т).

Значения

корреляционной

функции

при х

0 не

могут

быть

больше

ее

начального

значения.

Корреляционная функция имеет определенный смысл и для

детерминированных ограниченных неисчезающих процессов

Пример

1. Пусть x(t)

—постоянное

воздействие

(t)

а.

Корреляционная

функция равна

(т)

lim

J-

Г-»оо

-Г

Корреляционная

функция постоянного воздействия равна квадрату этого

воздействия

Пример

2. Пусть x(t)

—гармоническое

воздействие

(t) = a sin

(<ot

+ ф).

Корреляционная функция равна

(т)

=»

-zTf

\ a

sin (со/ + ф) sin [со (t + т) + ф]

<#.

<р

Поскольку

подынтегральное выражение периодично, то, представляя интеграл

виде суммы интегралов с пределами от

•—

до

—

(k=

±2,

...), получим

2Я/СО

=-|^-

sin

(со/

ф)

sin

[со

т)

ф]

2я/со

~j—-

\ [cos сот — cos (со/

2сот + 2ф)] dt.

4я

214

СИСТЕМЫ

ПРИ

СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ

[ГЛ. 14

Но

гак как

2JT/G)

\ cos

(со/

2сот

+ 2ф) dt = О,

то

(х)

-у

cos

сот.

Корреляционная

функция гармонического воздействия частоты

и фазы

ср

не

зависит от фазы

ср

и представляет собой гармоническую функцию той же

частоты со, амплитуды -^-.

Если

случайный процесс содержит постоянную составляю-

щую, т. е. если среднее значение случайного процесса

отлич-

но

от

нуля,то

lim

(т) =

т%

Т->оо

Если

же случайный процесс с нулевым средним содержит гар-

моническую составляющую частоты со, то

lim

(Т) —

-£•

cos сот]

При

отсутствии в случайном процессе с нулевым средним таких

детерминированных составляющих

lim

(т) = 0,

Т-»оо

что свидетельствует об уменьшении зависимости между значе-

ниями

процесса с ростом разделяющего их интервала. Эти свой-

ства корреляционной функции используются при выделении по-

стоянных и гармонических составляющих из случайного про-

цесса.

Взаимная корреляционная функция

характеризует меру связи

двух

случайных процессов. Заменяя t

на

t — т, получим

Rxy

to =

M{x{t-x)y

(t)}

M{y

(t) x(t- т)} -

(- т).

Взаимная

корреляционная

функция при

изменении

сдви-

га х на

—т

изменяет

порядок

своих

индексов.

При

т = 0

(0)

M{x{t)y(t)}.

Начальное

значение

взаимной

корреляционной

функции

равно

среднему

значению

произведения

случайных

про-

цессов.

§14

ХАРАКТЕРИСТИКИ

СЛУЧАЙНЫХ

ПРОЦЕССОВ

215

Наконец,

если средние значения

процессов

x(t) и

y(t)

отличны

от

нуля,

то

lim

(т)

%~>оо

для

простоты изложения

мы

будем предполагать,

что в

случайных воздействиях постоянные

гармонические составляю-

щие

отсутствуют,

т. е.

корреляционная функция удовлетворяет

условию

(%)•=•-§.

Учет

постоянных составляющих

в тех

Т~»оо

случаях, когда

это

необходимо,

не

представляет

труда.

Спектральную плотность случайного процесса

(со)

опреде-

лим

как

двустороннее преобразование Фурье корреляционной

функции

/?х(т):

S*(«>)=

e-l™R

(r)dr.

(14.1)

—

оо

Согласно обратному преобразованию Фурье

<o)rfco.

(14.2)

Заменяя

(14.1)

т на

—т,

со на

—со

принимая

во

внимание

четность корреляционной функции, получаем

$х

(©)

(•—

СО).

Спектральная

функция

случайного

процесса

является

чет-

ной

функцией

частоты.

Двустороннее преобразование Фурье взаимной корреляцион-

ной

функции

(%)

определяет собой взаимную спектральную

плотность

ху

(со):

оо

(x)dr.

(14.3)

Обратное преобразование Фурье определяет взаимную корреля-

ционную функцию

по

спектральной плотности:

{<s>)d&.

(14.4)

Заменяя

(14.3)

т на

—т,

со на

—со

принимая

во

внимание

свойства взаимной корреляционной функции, получаем

Sxy

(—со),

216

СИСТЕМЫ

ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ

[ГЛ

Взаимная спектральная плотность при изменении частоты со на

—со изменяет порядок своих

индексов,

Полагая в

(14.2)

при

= 0, получаем

оо

J,(«))rf«o.

(14.5)

Отсюда видно, что дисперсия

пропорциональна площади

соответствующей спектральной плотности

(со).

Найдем иное

представление спектральной плотности. Введем финитную

функцию

X{t)

||Г

т>г

Для такой финитной функции справедлива формула

Парсеваля,

которым мы широко пользовались в предыдущей, 13 главе. Обо-

значим через

(j(o)

спектральную функцию

(t),

т. е.

оо

(JG>)=

e-*™x

{f)dt=

-оо

-Т

Тогда согласно формуле Парсеваля получим

со

оо

(t)dt

~ \ |*

(/©)!

do,

~Т

—оо

или,

после деления на

2Г

и перехода к пределу при

Г—»оо,

оо

\ х

(t) dt

lim

±r

(/со) |

d©.

(14.5')

lim

—

Левая часть этого выражения при

= 0 равна дисперсии

Поэтому

оо

Сопоставляя

(14.5')

и (14.5), заключаем, что

—

(со)

= lim

-^г

(/со)

= lim —

(До)

/о).

(14.6)

Г-»оо

Г->оо

Спектральная

плотность

представляет

собой

предел

отно-

шения

спектральной

энергии

финитной

функции

интер-

валу

длительности

при

неограниченном

возрастании

по-

следнего.

Спектральная

плотность,

таким

образом,

опре-

деляет

мощность

случайного

процесса.

14.2]

ХАРАКТЕРИСТИКИ

СЛУЧАЙНЫХ ПРОЦЕССОВ 21?

Для взаимной спектральной плотности, аналогично (14.6),

будем иметь

(v)

}^1^

О'<°)

/<*)•

(14.7)

Найдем корреляционные функции и спектральные плотности

суммы

двух

случайных процессов. Пусть

Корреляционная

функция

(т)

равна

Яг

(Т)

= М {(X (t) +

(t)) (X(t + x) +

y(t

+ Т))},

ИЛИ

(т)

{*(*)*(*

т)}

{*(0#(*

т)}

Первое и четвертое слагаемые представляют собой корреля-

ционные

функции

(t)

(r)

второе и третье представляют

собой взаимно корреляционные функции

y(i)

(t)-

Таким

образом,

Я*

(т) +

/?*„

(т) +

(т).

(14.8)

Так

как спектральная плотность есть преобразование Фурье от

корреляционной

функции, то

(со) =

(со) +

(0).

(14.9)

Если процессы у

z независимы, то их взаимные корреляцион-

ные функции равны нулю, соответствующие им спектральные

плотности также равны нулю, т. е.

(©)

(СО)

= 0,

и,

следовательно, из (14.8), (14.9) получаем

Rz(*)

RxW

{*)

(НЛО)

(ai)

{(o)

Sy((o).

(14.11)

Итак,

если

процессы

x(t) и y(t)

независимы,

то

корреляционная

функция их

суммы

равна

сумме

корреляционных

функций

составляющих,

спектральная

плотность

суммы

состав-

ляющих

также

равна

сумме

спектральных

плотностей

от-

дельных

составляющих.

218

СИСТЕМЫ

ПРИ

СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ

[ГЛ

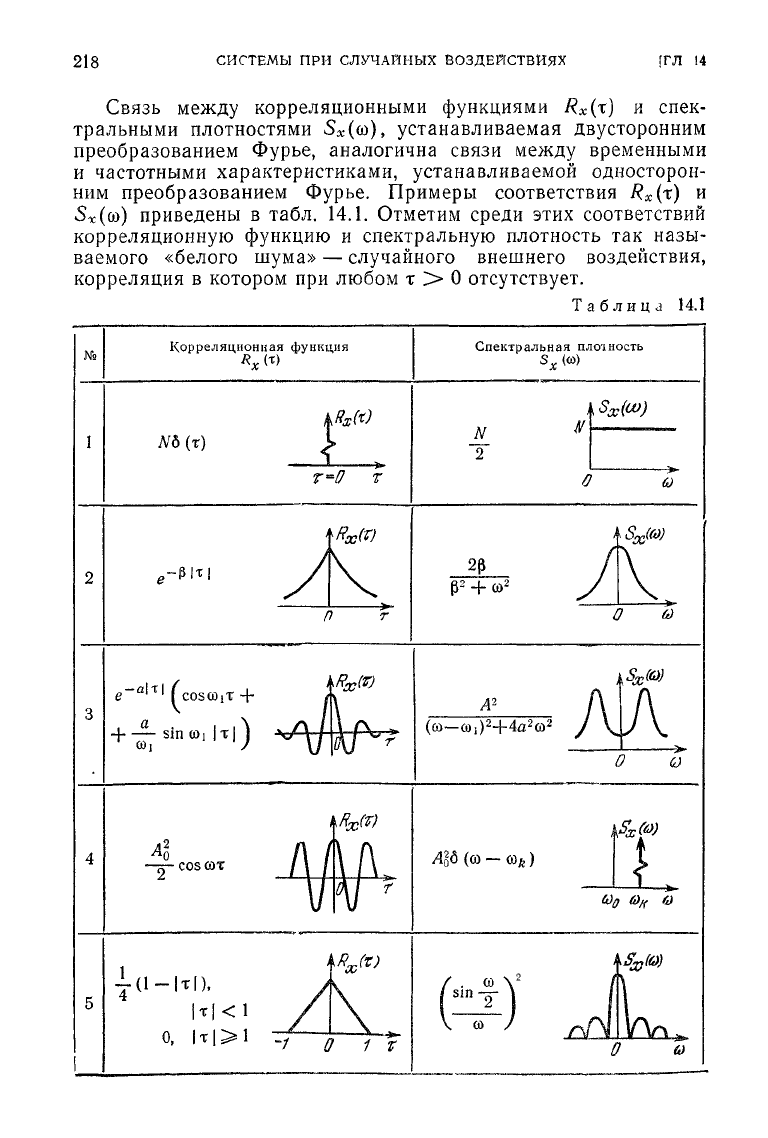
Связь

между

корреляционными функциями

(t)

спек-

тральными плотностями

(co),

устанавливаемая двусторонним

преобразованием Фурье, аналогична связи

между

временными

частотными характеристиками, устанавливаемой односторон-

ним

преобразованием Фурье. Примеры соответствия

(x)

((о)

приведены

табл.

14.1.

Отметим среди этих соответствий

корреляционную функцию

спектральную плотность

так

назы-

ваемого

«белого

шума»

—

случайного внешнего воздействия,

корреляция

котором

при

любом

т > 0

отсутствует.

Таблица

14.1

Корреляционная

функция

Спектральная

плотность

N6(x)

ft!)

(со—coi)

+4a

•

cos

сот

\Я

(Т)

О,

со

sin-у

(o)

14.31

СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ

219

Для

белого

шума

корреляционная

функция

представляет

собой

Ь-функцию, а

спектральная

плотность

постоянна.

Это значит, что белый шум обладает гармоническими состав-

ляющими

всех частот от 0 до оо одинаковой интенсивности.

14.3. Статистические характеристики автоматической системы

Рассмотрим линейную систему, обладающую частотной

характеристикой /((/со) и временной характеристикой k(t). Обо-

значим

через

{x)

(co)

корреляционную функцию и спек-

тральную плотность входной величины. Определим статистиче-

ские

характеристики выходной величины системы. По определе-

нию

взаимной спектральной плотности

$zx

(ю)

-2yr

(/со)

(— /со),

или,

после очевидного преобразования,

$гх(®)—

Т^Т~Т

"от"

)

(14.12)

Если

условиться,

что

(/оо)

—

то,

принимая во внимание выражение

(со)

(14.6), получаем

из

(14.12)

(со) =

/С

(/со)

(0).

(14.13)

Взаимная

спектральная

плотность

входной

выходной

величин

линейной

системы

равна

произведению

спект-

ральной

плотности

входной

величины

на

частотную

ха-

рактеристику

системы.

Рассмотрим еще спектральную плотность выходной вели-

чины,

которую, аналогично (14.6), можно представить в виде

(CD)=

lim

-L-1

(/со) |

, (14.14)

или,

после очевидного преобразования,

{®)=

/, '* - lim •

(—

/со)

(/со). (14.15)

T->co

Лг

\ /

Г->оо

Принимая

во внимание (14.12) и (14.15), получаем

22Э

СИСТЕМЫ

ПРИ

СЛУЧАЙНЫХ

ВОЗДЕЙСТВИЯХ

[ГЛ

Спектральная

плотность

выходной

величины

линейной

си-

стемы

равна

произведению

взаимной

спектральной

плот-

ности

на

сопряженную

частотную

характеристику

системы.

Исключая

из (14.13) и (14.16) взаимную спектральную плот-

ность

Szx(co),

получаем основное соотношение, связывающее

спектральные плотности входной и выходной величин:

[о).

(14.17)

Спектральная

плотность

выходной

величины

линейной

си-

стемы

равна

произведению

спектральной

плотности

вход-

ной

величины

на квадрат

модуля

частотной

характеристи-

ки

линейной

части

системы.

Соотношения

(14.13), (14.16) и особенно (14.17) играют важ-

ную роль при исследовании стохастических процессов в автома-

тических системах.

Если

подать на вход линейной системы воздействие x(t) вида

«белого шума», спектральная плотность которого равна единице,

т. е.

S*(co)=l,

то при этом из (14.13) получаем

ZJC

(CD)

/C(/(D).

(14.18)

Переходя от спектральных плотностей к корреляционным функ-

циям,

а от частотных

характеристик

—

к временным, получим

из

(14.18)

Rzx(t)

k(x).

(14.19)

При

подаче

на

вход

линейной

системы

воздействия

типа

«белого

шума»

взаимная

спектральная

плотность

равна

частотной

характеристике

системы,

а взаимная

корреля-

ционная

функция

равна

временной

характеристике.

Зная

спектральную плотность выходной величины линейной

системы, легко

определить

ее дисперсию по формуле

(со)

<ico

или,

на основании соотношения (14.17),

оо

№

* ^

dC0

(

}

°)

Эта формула лежит в основе исследований случайных процес-

сов в автоматических

системах.

СРЕДНЕКВАДР

ЭТИЧЕСКОЕ

ОТКЛОНЕНИЕ

221

14.4.

Среднеквадратическое отклонение

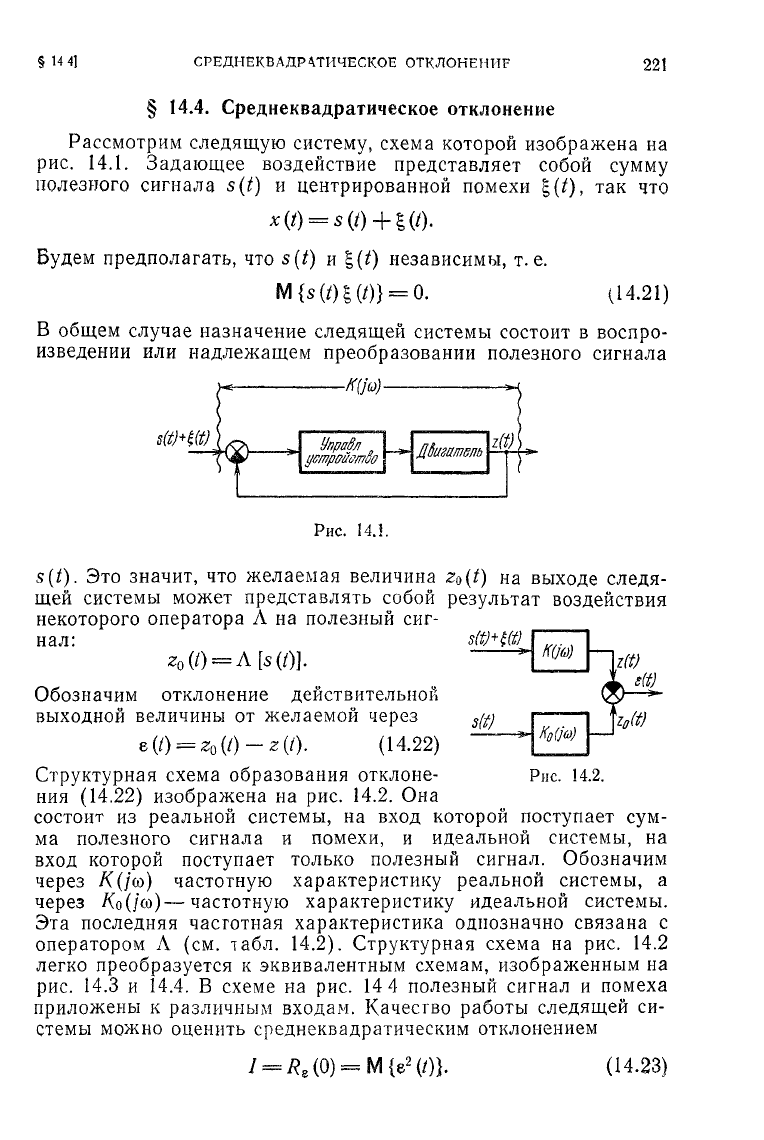
Рассмотрим следящую систему, схема которой изображена

на

рис.

14.1.

Задающее воздействие представляет собой

сумму

полезного сигнала

s(t)

центрированной помехи

£(/),

так что

5(0+

£(/)•

Будем предполагать,

что s(t) и

l(t)

независимы,

т.е.

M{s(t)l(t)}

(I4.21)

В общем

случае

назначение следящей системы состоит

воспро-

изведении

или

надлежащем преобразовании полезного сигнала

sltH

Управл

стройот

ДЫйт&ль

z(t)

Рис.

14.!.

s(t).

Это

значит,

что

желаемая величина

(t)

на

выходе

следя-

щей

системы может представлять собой

результат

воздействия

некоторого оператора

А на

полезный

сиг-

нал:

Обозначим отклонение действительной

выходной величины

от

желаемой через

Структурная схема образования отклоне-

Рис.

14.2.

ния

(14.22)

изображена

на рис. 14.2. Она

состоит

из

реальной системы,

на

вход

которой поступает

сум-

ма полезного сигнала

помехи,

идеальной системы,

на

вход

которой поступает только полезный сигнал. Обозначим

через

/С(/со)

частотную характеристику реальной системы,

через

Ко

(/со)—частотную

характеристику идеальной системы.

Эта последняя частотная характеристика однозначно связана

оператором

Л (см.

табл. 14.2). Структурная схема

на рис. 14.2

легко преобразуется

эквивалентным схемам, изображенным

на

рис.

14.3 и 14.4. В

схеме

на рис. 14 4

полезный сигнал

помеха

приложены

различным входам. Качество работы следящей

си-

стемы можно оценить среднеквадратическим отклонением

(0)

М{е

(/)}.

(14.23)