Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

192

ОПТИМАЛЬНЫЕ

ПРОЦЕССЫ

!ГЛ.

Максимальное

отклонение

e(t)

(рис. 13.2):

/ =

тах|е(/)|,

0</

< оо.

Интегральное

абсолютное

отклонение

е(/)

(рис.

13.3,а):

/=5

\e{t)\dt.

Интегральное

квадратическое

отклонение

(рис.

13.3,6):

(0л.

Чем меньше /, тем лучше система. Для идеальных систем

и,

значит,

/ssO.

{ISA)

Но,

как уже неоднократно подчеркивалось, идеальные системы

реализовать невозможно, и, следовательно, тождества (13.1) до-

стигнуть нельзя. Поэтому для оп-

тимальных систем показатель ка-

чества / достигает минимума, во-

обще говоря, отличного от нуля.

Выбор функционалов, соответ-

ствующих показателю качества,

представляет собой трудную за-

дачу,

так как он связан с учетом

Рис.

13.2.

многих конкретных условий, как, например, требования,

предъ-

являемые к системе, простота последующего определения опти-

мальной системы и т. п.

Часто,

помимо показателя качества, необходимо принять во

внимание

ограничения, налагаемые на переменные системы. Эти

ограничения

могут быть заданы в виде

|8(i)!<%

(13.2)

или

de(t)

(13.3)

131]

ПОКАЗАТЕЛИ

КАЧЕСТВА

193

или,

наконец,

de (t)

~&Т~)

(13.4)

Ограничения (13.2),

(13,3)

требуют, чтобы отклонение

s(t)

или

его производная

k\t)

по

абсолютной величине

не

превосходили

заданных значений.

Что же

касается ограничения (13.4),

то

оно

не

допускает быстрых изменений отклонения

&(t).

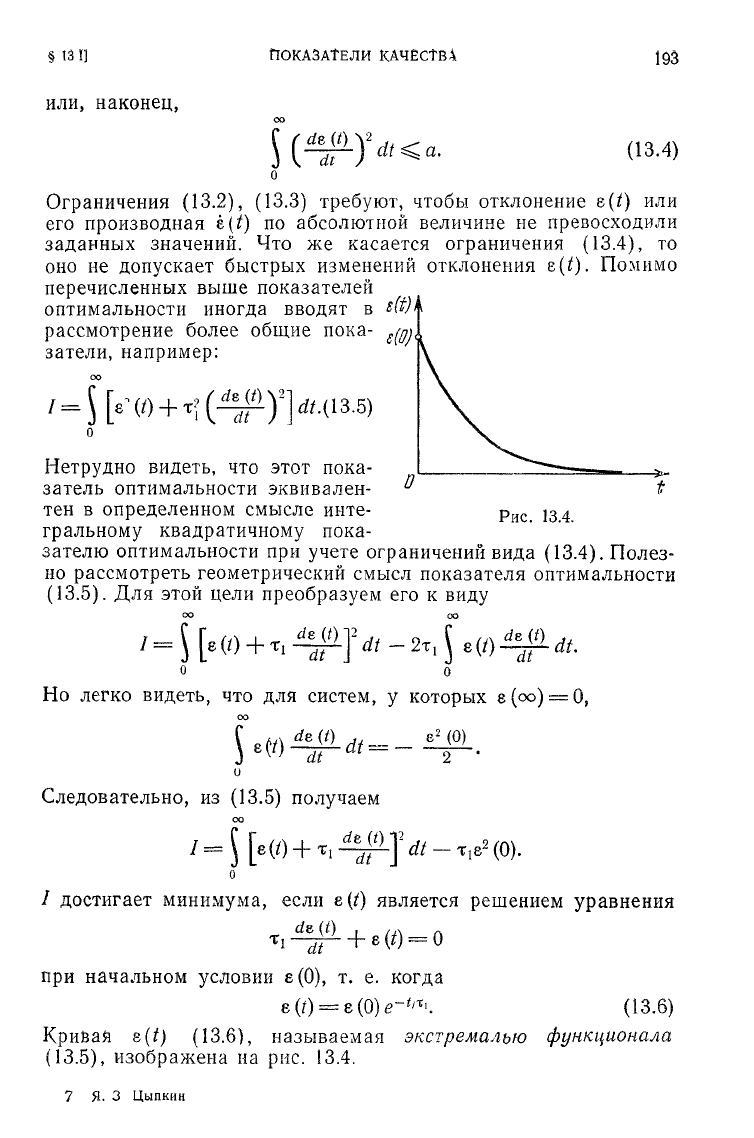
Помимо

перечисленных выше показателей

оптимальности иногда вводят

рассмотрение более общие пока-

затели, например:

Рис.

13.4,

Нетрудно видеть, что этот пока-

затель оптимальности эквивален-

тен в определенном смысле инте-

гральному квадратичному пока-

зателю оптимальности при

учете

ограничений вида (13.4). Полез-

но

рассмотреть геометрический смысл показателя оптимальности

(13.5). Для этой цели преобразуем его к виду

Но

легко видеть, что для систем, у которых

е(оо)

АЛ

<*г

(t)

. _

(0)

Следовательно, из

(13.5)

получаем

достигает минимума, если

е(/)

является решением уравнения

при

начальном условии

е(0),

т. е. когда

(/)

е(0)

е-''*'.

(13.6)

Крийай

e(t)

(13.6), называемая

экстремалью

функционала

(13.5), изображена на рис. 13.4.

Я. 3

Цыпкин

194

ОПТИМАЛЬНЫЕ

ПРОЦЕССЫ

[ГЛ

Экстремаль для интегрального квадратичного функционала

получается из (13 6) при

TI->0.

Она совпадает с осями коорди-

нат

и соответствует идеальной системе.

13.2. Интегральное квадратическое отклонение

Рассмотрим способ вычисления показателя качества инте-

грального квадратического отклонения. Будем предполагать, что

автоматическая система устойчива, ибо только в этом случае по-

казатели оптимальности, о которых шла речь в § 13.1, имеют

смысл. Для устойчивой системы показатель качества

оо

(t)dt

(13.7)

существует и конечен. Согласно обратному преобразованию

Фурье

оо

\Ь.

(13.8)

Умножим обе части (13 8) на

z(t)

и проинтегрируем полученное

равенство

по

t от 0 до оо. Тогда после изменения очередности

интегрирования

получим

оо оо

оо

—

(0 dt

-L

(/©)

е**

d<a.

(13.9)

Замечая,

что

со

е№

(— /со)

представляет собой спектральную функцию, сопряженную

ЕЦы),

получаем из (13.9)

{t) dt

У©)

dm. (13.10)

—оо

Соотношение

(13 10) часто называется

формулой

Парсеваля и

выражает тот факт, что

энергия

отклонения

ошибки

от

установившегося

значения

пропорциональна

интегралу

от квадрата

модуля

спек-

тральной

функции

этого

отклонения.

ИНТЕГРАЛЬНОЕ

КВДДРАТИЧЕСКОЕ

ОТКЛОНЕНИЕ

195

Обозначим

спектральную

энергетическую

функцию,

или

спектральную

плотность

энергии,

через

Э8

(со),

т. е.

Тогда из (13.10) находим

2jt

(©)

do,

(13.11)

т. е.

квадратическое

интегральное

отклонение

равно

пло-

щади

спектральной

плотности

энергии,

поделенной

на

2я.

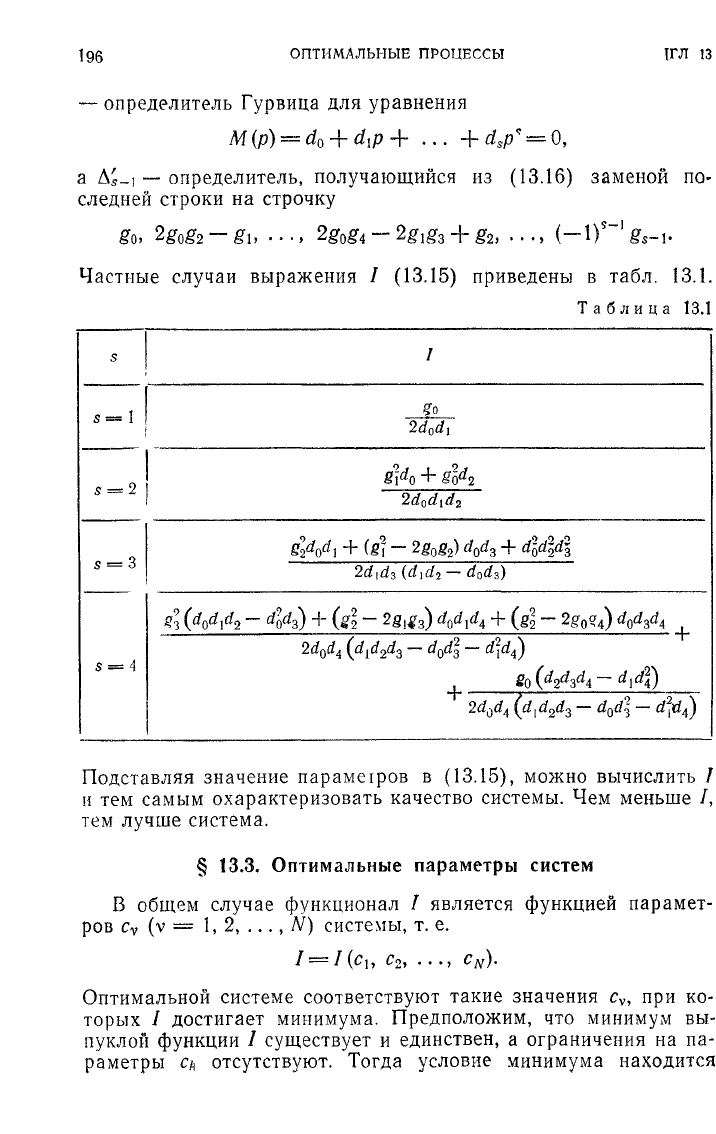
Таким

образом, если изве-

стен график

(co),

то / мож-

но

определить графически

(рис.

13.5). Интегральное ква-

дратическое отклонение можно

вычислить аналитически через

коэффициенты

спектральной

плотности энергии ошибки.

Пусть изображение отклоне-

ния

e(t) представимо в виде

дробно-рациональной функции

(oy

ис

135

от

/?,

которая имеет вид

Е(р)

Тогда

и,

значит,

MAP)

(/о)

«5-1

2я

dip

+ ...

(/0

P=l®

(/со)

rfco.

(13.12)

(13.13)

(13.14)

Эгот

интеграл можно вычислить с помощью обычных методов

теории функций комплексного переменного и выразить через

коэффициенты

изображения Е(р) (13.12). Опуская несколько

громоздкие вычисления, приведем окончательные результаты:

где

K-V

•if

A-i

(13.15)

(13.16)

196

ОПТИМАЛЬНЫЕ ПРОЦЕССЫ

—

определитель Гурвица для уравнения

1ГЛ

As-i

— определитель, получающийся

из

(13.16)

заменой

по-

следней строки

на

строчку

Частные случаи выражения

(13.15)

приведены

табл.

13.1.

Таблица

13.1

—

rf,

'2rft?

(gi

—

)

rfgrfg^

2dids

(d\d<z

—

dod%)

•

I •

—

с?з

—

{

)

Подставляя значение параметров

(13.15), можно вычислить

тем

самым охарактеризовать качество системы.

Чем

меньше

тем лучше система.

13.3.

Оптимальные параметры систем

В общем случае функционал

является функцией парамет-

ров

(v = 1, 2, ..., N)

системы,

т. е.

(с

...,

Оптимальной системе соответствуют такие значения

при ко-

торых

достигает минимума. Предположим,

что

минимум

вы-

пуклой функции

существует

единствен,

ограничения

на па-

раметры

си

отсутствуют.

Тогда условие минимума находится

13 3] ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ СИСТЕМ

197

приравниванием частных производных от /

по

нулю, т. е.

—i-i-^L

v—!,.,.,#.

(13.17)

Введем

векторные обозначения:

, ...,

)

— вектор-столбец параметров,

V/(с)

grad/(с)

д!

(с)

дЦс)

<э<\

дс

дЦе

дс

N )

— градиент-вектор-столбец частных производных.

Тогда

систе-

му уравнений

(13.17)

можно записать в виде одного векторного

уравнения:

{с)

= 0.

Решение этого уравнения

определяет оптимальный вектор

па-

раметров

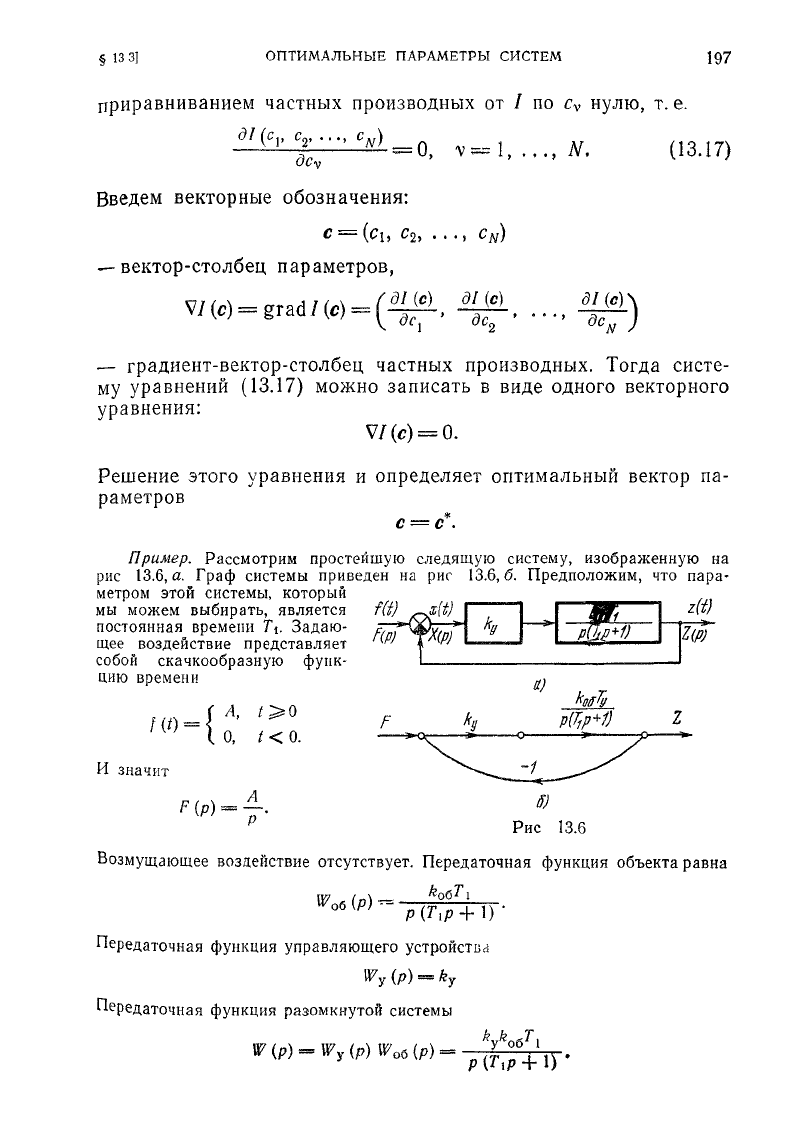
Пример.

Рассмотрим простейшую следящую систему, изображенную на

рис 13.6,

а.

Граф системы приведен на рис 13.6, б. Предположим, что

пара-

метром этой системы, который

мы можем выбирать, является f(t)

^j,[t)

Г~~™~~"1

ШГ,

zffl

постоянная

времени

Т\.

Задаю-

щее воздействие представляет

собой скачкообразную функ-

цию времени

а)

fit)

значит

"to,

pUip+a

(p)

—.

б)

Рис

13.6

Возмущающее воздействие

отсутствует.

Передаточная функция объекта равна

Передаточная функция управляющего устройства

(p)

Передаточная функция разомкнутой системы

198

ОПТИМАЛЬНЫЕ

ПРОЦЕССЫ [ГЛ.

Следовательно, передаточная функция замкнутой системы по задающему воз-

действию

будет

равна

(р)

kkj.

Подставляя выражения для

К(р)

и F(p) в уравнение замкнутой системы

X{p)

[l-K(p)]F(p),

получим

(р)

„

Поскольку установившееся значение

ошибки

равно

lim

то

£(p)

Z(p)

— ^

_ .

(13 18)

Сопоставляя

(13,18)

(13.12)

заключаем,

что s

2 и

—

Пользуясь табл 13 1, находим для

- (

Рис.

13.7.

(13.19)

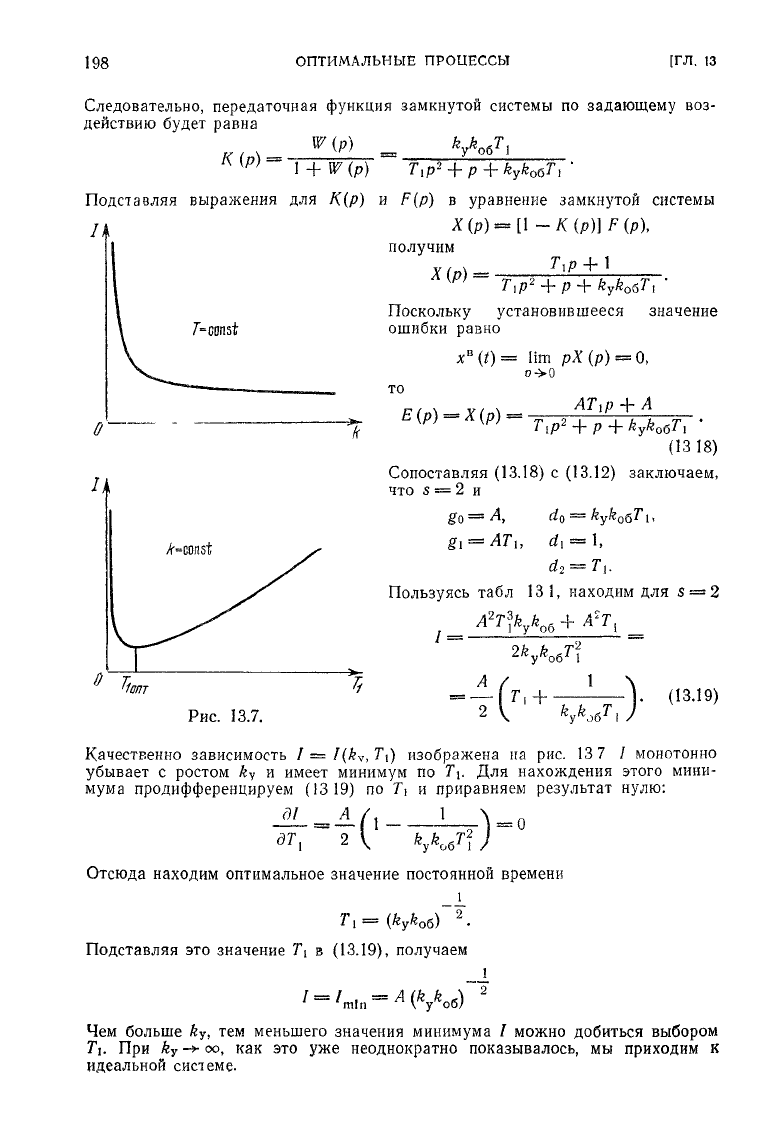
Качественно зависимость / =

I(k

,T\)

изображена на рис. 13 7 / монотонно

убывает

с ростом

и имеет минимум

по

Для нахождения этого мини-

мума продифференцируем (13 19) по Т\ и приравняем

результат

нулю:

д!

(

* V

ККб

Отсюда находим оптимальное значение постоянной времени

Подставляя это значение Т\ в (13.19), получаем

-1

Чем больше

тем меньшего значения минимума / можно добиться выбором

Т\. При

оо, как это уже неоднократно показывалось, мы приходим к

идеальной системе.

§13 4] ОПТИМАЛЬНЫЕ

ХАРАКТЕРИСТИКИ

СИСТЕМ

19§

13.4. Оптимальные характеристики систем

Рассмотрим автоматическую систему, изображенную

на

рис.

13.8.

Обозначим через

Q(P)

передаточную функцию неиз-

меняемой

часги

системы

—

объек-

z(t)

цш

(p)

Up)

та,

через

(p)—

передаточную

f(i)

^Ш

функцию

управляющего устрой-

ства.

Задача определения опти-

мальных характеристик

систе-

мы состоит

определении пере-

Рис

даточной функции

(p)

или ча-

стотной характеристики

(j(x))

изменяемой части системы

—

управляющего устройства,

при

котором показатель оптималь-

ности

достигает экстремума.

В качестве таких показателей можно выбрать:

Интегральное квадратическое отклонение

в*

(О

Л.

(13.20)

2. Энергию управления

где

(

)

*(/)-

х-

(0,

(/)

(t)

и-

(0.

(13.22)

Поскольку

одновременно невозможно достигнуть оптимума

по

двум

различным

показателям,

то

можно сформулировать

три за-

дачи оптимизации: определить оптимальные характеристики

си-

стемы,

при

которых:

достигается минимум

при

условии,

что

Ни

2) достигается минимум

при

условии,

что

;

3) достигается минимум

оо

(t)

хЧ(/)]

at,

(13.23)

где

—

некоторое число, характеризующее

«вес»

функциона-

ла

Займемся

решением более общей третьей задачи.

На

основа-

нии

соотношения

(13.10)

получаем

* ^

200

ОПТИМАЛЬНЫЕ

ПРОЦЕССЫ

[ГЛ.

Для простоты и наглядности предположим, что вынужденные

или

установившиеся значения ошибки и управляющего воздей-

ствия равны нулю, т. е.

Тогда, как видно из

(13.22),

вместо

(13.24)

будем

иметь

оо

I=\[x

(t)

(0]

А"

(/со)

Я.

(/(о)

Р]

dco.

оо

(13.25)

Но,

как это непосредственно

следует

из блок-схемы системы

(рис.

13.8),

Х(/со)

-/С

(/со)]

(/со)

Подставляя значения спектральных функций ошибки

Х(/со)

управления

f/(/со)

в (13.25), получим

/ =

тг-

(/со)

(/«)

(13.26)

Введем обозначения спектральной энергии задающего воз-

действия

спектральной энергии управляющего воздействия

$эи

е0

)

(/со)

(/©)

Тогда

(13.26)

можно окончательно записать в следующей форме:

(13.27)

Если

подставить в

(13.27)

значения спектральных энергий и

частотной характеристики замкнутой системы, в которую входит

часть неопределенных параметров, то мы придем к задаче опре-

13.4]

ОПТИМАЛЬНЫЕ

ХАРАКТЕРИСТИКИ

СИСТЕМ

201

деления оптимальных параметров, рассмотренной в § 13.3. Более

общая задача состоит в нахождении оптимальной частотной ха-

рактеристики

/Сопт(/(о)

или передаточной функции замкнутой си-

стемы

/Сопт(р),

для которой функционал /

(13.27)

достигает сво-

его минимума. Для решения этой задачи преобразуем функцио-

нал /

(13.27)

к более удобному

виду.

Замечая, что

(/со)

—

[^С

(/со)

/со)]

(fa)

К (-

/со),

обозначая

S,(«))

(«B)

((o),

(13.28)

запишем функционал /

(13.27)

в виде

(со)

к (/со) к (

/со) s

((o)

[К

(/со) +

/со)]

(со)}

dco.

Если

подынтегральном

выражении

прибавить

вычесть

сла-

(©)

гаемое

то

после

очевидных

преобразований

получаем

(СО)

выражение функционала в наиболее удобной форме:

(13.29)

Удобство

такого представления функционала состоит в том, что

искомая

частотная характеристика

/((/со)

входит

только в одно

слагаемое подынтегрального выражения. А так как слагаемые

в подынтегральном выражении неотрицательны, то минимиза-

ция

/ сводится к минимизации слагаемого

зависящего от

(/со),

или

что то же, к минимизации

(со)

= |

/С

(/ш)

(<о)

—

(со)

Очевидно, что если не наложить требования реализуемости

на

(/со), то / достигает минимума при обращении Л (со) в нуль,

т. е. при

/((/со),

равном

(со)

•