Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

222

СИСТЕМЫ

ПРИ

СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ

ГГЛ

Таблица

14.2

(O=A[s(O]

s(t)

s'(t)

s"{t)

(T)

(t +

)

(/(0)

/CO

(/CO)

/CO

Название

воспроизведение

дифференцирование

двойное

дифференцирование

интегрирование

упреждение

Чем меньше

эта

величина,

тем

выше качество системы. Анало-

гично (14.5)

(14.24)

Для

того

чтобы воспользоваться соотношением (14.24), необхо-

димо прежде всего определить спектральную плотность отклоне-

ния

е(0-

Предположим,

что

спектральные плотности полезного

/лД_

sit)

Рис.

14.3.

Рис.

14.4.

сигнала

помехи равны соответственно

(co)

S^(со);

тогда

по

формуле

(14.17)

находим составляющие спектральной плот-

ности

отклонения

^Со

(/«>)

—

/С

(/со)

(со)

|/C(/©)I

соответствующие полезному сигналу

помехе.

Так как

спек-

тральная плотность алгебраической суммы независимых процес-

сов равна сумме спектральных плотностей составляющих,

то

(а)

/Со

О©)

(/«)

(со)

(/(о)

(<о).

14.4]

СРЕДНЕКВАДРАТИЧЕСКОЕ

ОТКЛОНЕНИЕ

223

Подставляя значение

(co)

в (14.24), находим выражение сред-

неквадратического отклонения:

. (14.25)

При

известных частотных характеристиках и спектральных плот-

ностях выражение для / можно привести к виду

2я

(/со)

(14.26)

где

(/(o)

(/со)—полиномы

по /со. Для вычисления можно

применить

формулы предыдущей главы и табл. 13.1. Поскольку

/ является функцией параметров системы, то можно поставить

вопрос об определении оптимальных параметров. Оптимальные

параметры с = с*

могут

быть найдены, как отмечалось ранее,

из

условия

Отметим, что в вычислительных процедурах нет принципиаль-

ного различия

между

детерминированной задачей минимизации

интегрального квадратического отклонения и статистической за-

дачей минимизации среднеквадратического отклонения.

Пример.

Рассмотрим следящую систему,

структура

которой изображе-

на

на рис. 14.5. Предположим, что входной сигнал представляет собой ряд

f(tH(t)H(t)

lit)

Zip)

Рис,

14.5.

скачкообразных поворотов на случайные

углы

в случайные моменты времени:

s (t)

dkl

(t —

tk)

где 1

(t)

— единичная скачкообразная функция времени:

1 для

>°>

0 для t < 0.

Интервалы

—

tk-i

являются независимыми случайными переменными, имею-

щими

одну и ту же функцию распределения вероятности, а все

также пред-

ст

авляют

собой независимые случайные переменные, обладающие одной и

29л

СИСТЕМЫ

ПРИ

СЛУЧАЙНЫХ

ВОЗДЕЙСТВИЯХ

[гл.

той же функцией распределения

вероятности,

Пусть значение спектральной

плотности производной входного сигнала равно

(со)

Предположим, далее, что в устройстве, измеряющем ошибку, содержится ис-

точник

помех, так что выходной сигнал сравнивающего устройства равен

s(t) — z(t) +

l(t)

где

l(t)

представляет собой чисто случайный стационар-

ный

процесс (белый шум), обладающий спектральной плотностью

(со)

В.

Наконец,

предположим, что помехи и производная от сигнала независимы,

т. е.

Ограничимся применением стабилизирующего устройства с неизменной по-

стоянной

времени Т\ и

будем

изменять его коэффициент усиления

k\.

В этом

случае

выходное напряжение стабилизирующего устройства определится урав-

нением

Уравнение движения двигателя имеет вид

где / представляет собой

сумму

моментов инерции двигателя и нагрузки,

— коэффициент

противоэлектродвижущей

силы или жидкостного трения,

&з

— удельный выходной момент, и — входное

напряжение.

Если теперь поло-

жить"

J/k

и исключить из этих уравнений переменную

и,

то получим

Единственным изменяемым параметром является коэффициент

k\.

Следует

за-

метить, что в

левую

часть этого дифференциального уравнения

входят

по-

мехи и только производные входного сигнала. Следовательно, спектральная

плотность производных входного сигнала занимает в нашем анализе место

обычной входной спектральной плотности. В связи с этим можно записать

(со)

- | 1 -

(/со) |

(со) + |

(/со) !

^ (со),

где

(/со)

- .

(/со)

+ (Г, +

)

(/со)

+ /со +

Формула для

(/со) может быть приведена к более удобному

виду

с помощью

замены переменных:

{

со

Г,

(Т

)

14.5]

ОПТИМАЛЬНЫЕ

СИСТЕМЫ

225

Величина

неизменна и меньше или равна

для всех положительных зна-

чений

Т\ и

представляет собой усиление, величину которого можно ме-

нять.

При этом среднее значение квадрата ошибки равно

оо

858

2я

оо

О*

(/0)

(jib)

/ш

+ a |

Вычисляя

среднее значение квадрата ошибки, окончательно получаем

где

-сф)

2ЛГ

Для того чтобы найти минимум /, продифференцируем / по коэффициенту

усиления

и приравняем производную нулю. Полученное уравнение

будет

урав-

нением

второй степени относительно а. Только один из его корней, а именно

соответствует области устойчивости Подставив

ссо

в выражение для /,

нахо*

дим минимальное значение

/mm:

14.5.

Оптимальные

системы

Задача синтеза оптимальных систем при случайных

воздей*

ствиях состоит в определении их характеристик, при которых

среднеквадратическое отклонение /

достигает

минимума. Для

решения этой задачи преобразуем выражение

(14.25)

к такой

форме:

(14.27)

Легко видеть

сходство

выражения для среднеквадратического

Уклонения

(14.27)

с выражением для интегральной ошибки

Детерминированной системы /. Поэтому для решения задачи син-

теза

мы можем воспользоваться уже известными результатами,

Я, 3

Цыпкин

226

СИСТЕМЫ

ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ [ГЛ.

изложенными

в гл. 13. Из

сопоставления

(13.27)

(14.27)

за-

ключаем,

что

(/со)

соответствует

(/co)/iCo

(/<*>)>

(со)

соответствует

(со),

(со)

соответствует

(со).

Множитель

|Ко(/со)

(14.27)

не оказывает влияния на условие

оптимальности. Подставляя соответствующие значения в

форму-

лу

(13.27)

оптимальной частотной характеристики

(/СО)

f(<o)

+ S

получим

/Со

(/со)

(со)

последнего выражения получим формулу для оптимальной

частотной передаточной

функции,

минимизирующей /:

/-• \

^о

(/СО)

(СО)

/1/1

OQ\

При этом, как легко установить,

Частотная характеристика

Копт

(/со), определяемая выраже-

нием

(14.28), физически нереализуема. Это

следует

из того, что

если найти временную характеристику

пт(т),

соответствую-

щую Копт

(/&>),

то при t

0 эта импульсная характеристика

бу-

дет отлична от нуля (см. приложение

1),

т. е.

(t)

0 при t < 0.

Это означает, что следствие (реакция на возмущение) предше-

ствует

причине (возмущению вида дельта-функции, приложен-

ному в момент времени t = 0). Для получения реализуемой оп-

тимальной

частотной характеристики можно использовать опе-

рации

факторизации и расщепления, аналогично тому как это

делалось в § 13.4. Представим

сумму

спектральных плотностей

виде произведения

двух

сомножителей, один из которых имеет

нули и полюсы в верхней полуплоскости со, а

другой

— в ниж-

ней:

(ш)

(со)

-1

(/со) |

(/со)

/со).

14-5]

ОПТИМАЛЬНЫЕ СИСТЕМЫ

227

Тогда

физически

реализуемая

оптимальная

частотная

характе-

ристика

будет

иметь

вид

(ш)—

]

Допт

1/СО)

-щ^

где выражение,

полученное

результате

расщепления,

(

Ко

(/со)

5Лео)

)

/CD)

имеет

нули

полюсы

верхней

полуплоскости

со.

Пример.

Пусть спектральная плотность сигнала равна

а спектральная плотность помехи

(со)

задача состоит

построении системы, осуществляющей фильтрацию

и диф-

ференцирование

этом случае

Ко

(/со)

/со

Для отыскания

/(опт

(/со) воспользуемся формулой (14.30). Произведем

опе-

рацию факторизации:

(со)

(ю)

_L_-

1±|1

(/а)

/со),

/со)

^ ^

(±/0)-

] ±/о)

Затем произведем операцию расщепления:

Ко

(ю)

1 + со

/со

/ю)

/со (1 + /со)

(V2

/©)

1 —/0

или

Ко

(/0)

(0) 1 /0 1 /0

(— /0)

д/2"

+ 1 1 + /0

+ 1

V2~—

Таким

образом,

/со

(

(- /о) j

1 1

/0'

Подставляя это выражение, а также значение

(/со) в формулу

(14.30\

получаем

пт

(/<*>)

Эта

частотная характеристика

соответствует

реальному дифференцирующему

Устройству

с коэффициентом усиления k

——-—

с постоянной вре-

мени

228

СИСТЕМЫ

ПРИ

СЛУЧАЙНЫХ

ВОЗДЕЙСТВИЯХ

[ГЛ,

Т4

14.6. Оптимальная стохастическая система

при

учете

ограничений

Обычно при проектировании систем характеристики управляе-

мого объекта являются заданными и изменить их невозможно.

Если

мы не

будем

учитывать ограничений, связанных с немини-

мально-фазовостью объек-

та, с запаздыванием в объ-

екте, то определение опти-

мальной передаточной

функции

системы по фор-

муле

(14.30)

приведет, во-

Рис.

14.6. обще говоря, к нереали-

зуемой передаточной

функции.

Действительно, из структурной схемы (рис. 14.6) сле-

дует,

что

(/со) _____

^г

Z (/со)

_г,

(/со)

/С

(/со)

-р-Щ

—

КЦ®)*

об

(/со)

U UC0)j

ТЩ"~

(j(o)

Предположим, что частотная характеристика объекта имеет вид

Пусть объект устойчив, но неминимально-фазовый, т. е.

W\(ja>)

имеет нижние нули со (р =

/со

— правые). В этом

случае

(/со)

F(/o)

Wi(la>)e-

{

(/со)

Из

этого выражения

следует,

что найденная частотная характе-

ристика

U(j(u)/F(j(o)

содержит нижние нули со, что соответствует

неустойчивой системе, и, кроме того, содержит упреждающие

звенья,

что соответствует нереализуемой системе.

Для того чтобы обойти эти трудности и получить устойчивую

оптимальную реализуемую систему, поступим следующим об-

разом.

Включим в искомую частотную характеристику

/((/со)

множитель

Wi(j®)e-№

так что

Таким

образом,

/((/со)

содержит нижние нули со и запаздыва-

ние

т. Теперь уже искомой функцией является

L(/co).

При та-

ком

выборе передаточной функции замкнутой системы получаем

(М)

га

(/со)

e~K»

(/со)

/(от

,. ,

F (/со)

ЯМ/со)

W^'

Таким

образом, частотная характеристика системы

/С(/оз)

долж-

на

содержать в качестве множителя частотную характеристику

ОПТИМАЛЬНАЯ

СИСТЕМА

ПРИ УЧЕТЕ

ОГРАНИЧЕНИЙ

229

неизменной

части. Найдем теперь

Кот

(/со) или

£опт(/со)

при

учете

ограничений, вызванных неизменной частью системы. Для

этой

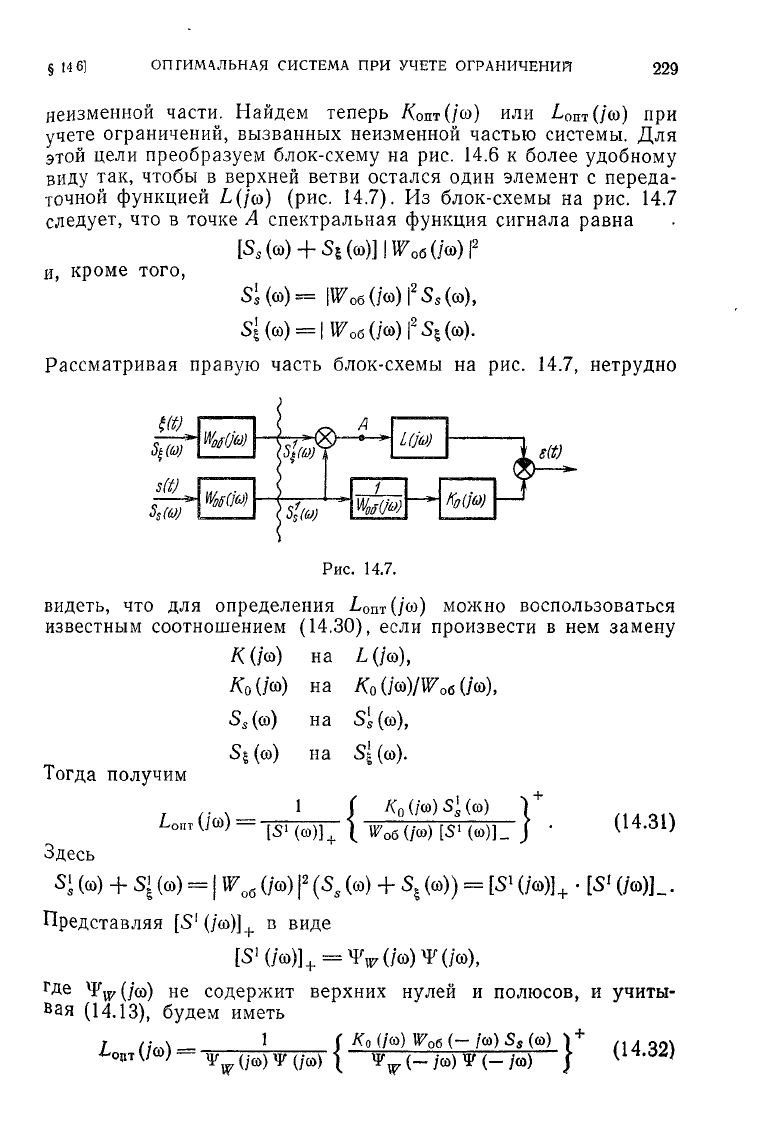
цели преобразуем блок-схему на рис. 14.6 к более удобному

виду так, чтобы в верхней ветви остался один элемент с переда-

точной функцией

L(/co)

(рис. 14.7). Из блок-схемы на рис. 14.7

следует,

что в точке А спектральная функция сигнала равна

и,

кроме того,

Si(©)=

Рассматривая правую часть блок-схемы на рис. 14.7, нетрудно

Рис.

14.7.

видеть, что для определения

(/co)

можно воспользоваться

известным соотношением (14.30), если произвести в нем замену

(/со) на

L(/G>),

/Со

(/©)

на

Ko(h)/W

(fa),

(G>)

на

Ss(co),

Тогда получим

на

S|(co).

*„(/<»)

S'(B>)

со)

(со)]

гГ-

(14.31)

{()]

Здесь

(со) +

(со)

(/со) |

(со)

(со))

[S>

(/co)]

•

(/©)]_.

Представляя

(/со)]

в виде

де

,(/co)

не содержит верхних нулей и

полюсов,

учиты-

вая (14.13),

будем

иметь

230

СИСТЕМЫ

ПРИ

СЛУЧАЙНЫХ

ВОЗДЕЙСТВИЯХ

[ГЛ.

и,

следовательно,

получаем

Копт

(/со)

onT

(/со).

(14.33)

Если

объект устойчив

минимально-фазовый,

то

(/со)

об

(/со);

тогда

у(

/(0

)

¥(-/©)

что совпадает

формулой (14.30).

В заключение отметим,

что

минимальные значения

которые

достигаются, когда оптимальная частотная характеристика

/(опт

(/со) нереализуема,

/i,

когда

/(опт

(/со) реализуема

/и,

и,

на-

конец,

когда /(опт (/со) реализуема

при

учете

ограничений,

удовлетворяют неравенствам

После

определения /(опт (/со)

для

замкнутой системы

(рис.

14.7)

нетрудно определить частотную характеристику упра-

вляющего устройства

(j(d)

из

очевидного соотношения

(yco)

(/со)

\ +

(/со)

•

Разрешая

это

соотношение относительно

1Г

(/со),

получим

опт

(/ш)

опт (/(о)

По

найденной таким образом частотной характеристике опти-

мального управляющего устройства можно определить

его

струк-

туру

параметры.

Задачи

14.1.

Пусть

f f

2cof

частотная характеристика

неизменной

части системы

(рис. 14.8)

равна

—у/со

1+f/co

ГДоказать,

что

оптимальная частотная характеристика управляющего устройства

ЗАДАЧИ

231

равна

оптимальная частотная характеристика корректирующего устройства равна

•1(0+1

При

этом

/mln

(0)

т. е. минимальное значение среднеквадратической ошибки тем меньше, чем

меньше

соь

fit/

jf*>JE(bJ

Wy(JQ)

Wf/п»

lit)

Рис.

14.8.

14.2. При тех же условиях, что и в предыдущей задаче, при частотной ха-

рактеристике неизменной части системы, равной

1*7

(/00)

*-^

показать, что оптимальные частотные характеристики

пт(/со)

№

(/со)

равны соответственно

onT

(/со)

минимальное значение среднеквадра-

тичной ошибки равно

Рис.

14.9.

14.3. Показать, что для системы, изображенной на рис. 14.9, при

спек»

2aa

тральной плотности входного воздействия

(со) =

—я—:—=-

дисперсия

ошиб*

-\-

со*

ки

и выходной величины равны соответственно

(

)

/^.2

_ Г

_,2