Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

252

ПРОЦЕССЫ

НЕЛИНЕЙНЫХ

СИСТЕМАХ

[ГЛ.

Для линейной системы,

силу (16.10),

это

уравнение принимает

особенно

простой

вид:

—

w{x)x

[t-x)dx.

(16.15)

Уравнение

(16.15) имеет единственное решение

(/)=:jK

(16.16)

соответствующее

состоянию

равновесия.

В нелинейных системах возможны, вообще говоря, несколько

состояний

равновесия. Полагая

(16.14)

(t)~

const,

по-

лучим

оо

—

{х

)

w{%)dx.

(16.17)

Передаточная функция

W(p)

линейной части системы связана

ее импульсной характеристикой преобразованием Лапласа

оо

W{p)=\

w(x)e~P

dx,

(16.18)

и, значит,

при

= 0

оо

W(0)=^w(x)dx.

(16.19)

Из уравнения (16.17) получаем

ф(ха

)

-тЙо)"*

(16

20)

Используя обозначение статического коэффициента линеариза-

ции

(15.6)

(*а)

^а)

(

ф Q)

(16.21)

перепишем

(16.20)

виде

(

)

>—

(0)

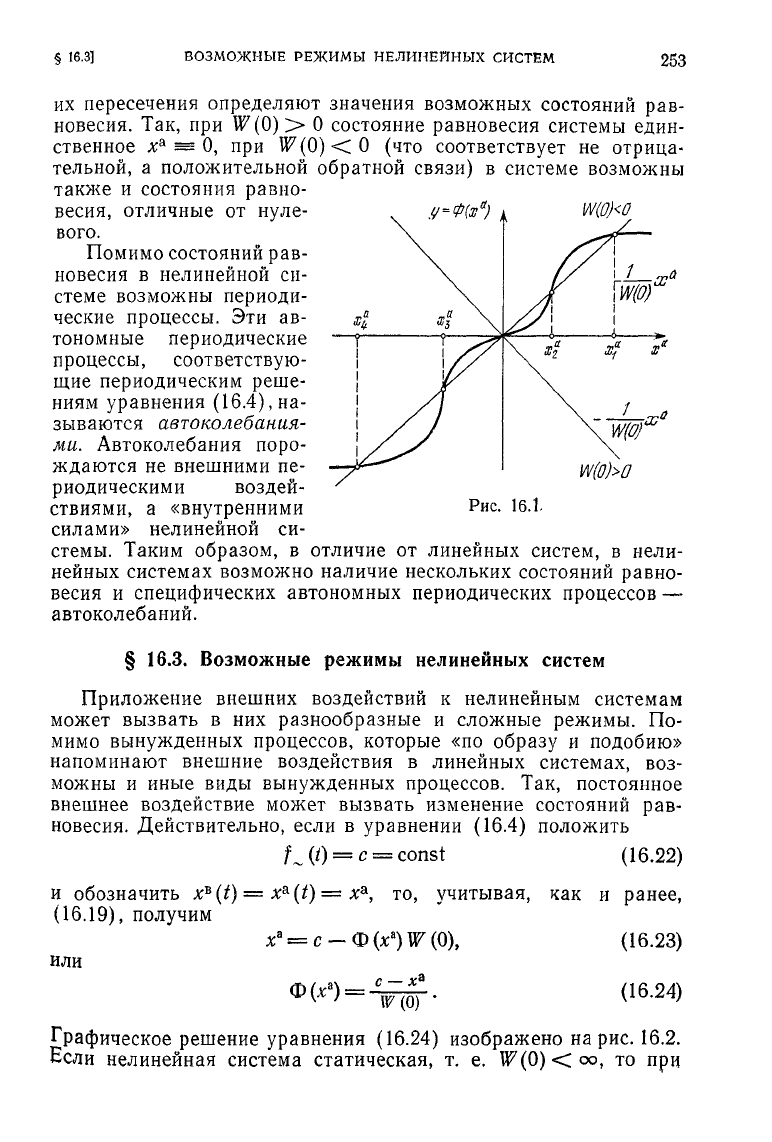
Для определения состояний равновесия воспользуемся уравне-

нием

(16.20). Проведем

на

графике нелинейной характеристики

ф(х

)

прямую

у —

—

(рис.

16.1). Абсциссы точек

§ 16.3]

ВОЗМОЖНЫЕ

РЕЖИМЫ НЕЛИНЕЙНЫХ СИСТЕМ

253

Рис.

16.1.

их пересечения определяют значения возможных состояний рав-

новесия.

Так, при

W(0)

О состояние равновесия системы един-

ственное

0, при

W(O)<CO

(что

соответствует

не отрица-

тельной, а положительной обратной связи) в системе возможны

также и состояния равно-

весия, отличные от нуле-

у=Ф{х

)

вого.

Помимо

состояний рав-

новесия в нелинейной си-

стеме возможны периоди-

ческие процессы. Эти ав-

тономные периодические

процессы,

соответствую-

щие периодическим реше-

ниям

уравнения (16.4), на-

зываются

автоколебания-

ми. Автоколебания поро-

ждаются не внешними пе-

риодическими воздей-

ствиями, а «внутренними

силами» нелинейной си-

стемы. Таким образом, в отличие от линейных систем, в нели-

нейных системах возможно наличие нескольких состояний равно-

весия и специфических автономных периодических процессов —

автоколебаний.

16.3.

Возможные

режимы

нелинейных

систем

Приложение внешних воздействий к нелинейным системам

может вызвать в них разнообразные и сложные режимы. По-

мимо вынужденных процессов, которые «по образу и

подобию»

напоминают внешние воздействия в линейных системах, воз-

можны и иные виды вынужденных процессов. Так, постоянное

внешнее воздействие может вызвать изменение состояний рав-

новесия.

Действительно, если в уравнении

(16.4)

положить

МО

const

(16.22)

и обозначить

(t)

то,

учитывая,

как и

ранее,

(16.19),

получим

x*^c-<D{x

)W(0),

(16.23)

или

^—тпг-

(16

24)

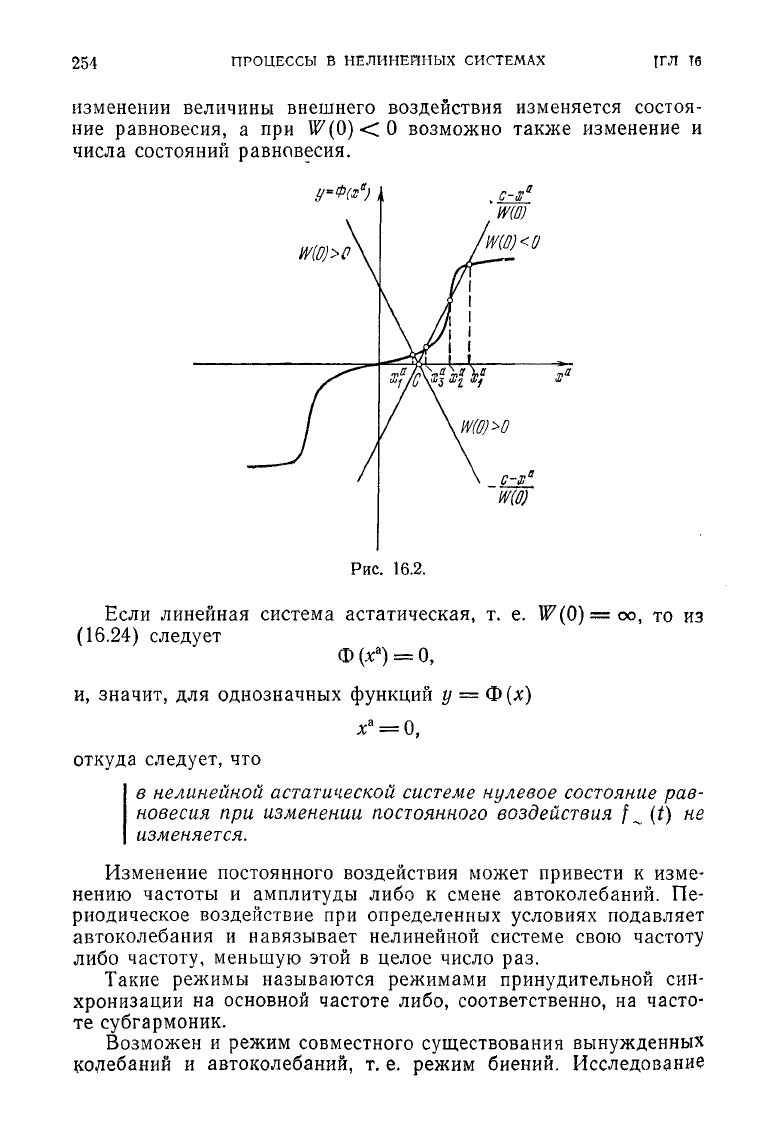
Графическое решение уравнения

(16.24)

изображено на рис. 16.2.

Если нелинейная система статическая, т. е.

W(0)<oo

то при

254

ПРОЦЕССЫ

В НЕЛИНЕЙНЫХ СИСТЕМАХ

[ГЛ

Тб

изменении

величины внешнего воздействия изменяется состоя-

ние

равновесия, а при

Щ0)<0

возможно также изменение и

числа состояний равновесия.

w(o)>o

Ш0)<0

Рис.

16.2.

Если

линейная система астатическая, т. е.

Щ0)=оо,

то из

(16.24)

следует

Ф(х

)

и,

значит, для однозначных функций у

ф(х)

откуда

следует,

что

нелинейной

астатической

системе

нулевое

состояние

рав-

новесия

при

изменении

постоянного

воздействия

(t) не

изменяется.

Изменение

постоянного воздействия может привести к изме-

нению

частоты и амплитуды либо к смене автоколебаний. Пе-

риодическое воздействие при определенных условиях подавляет

автоколебания и навязывает нелинейной системе свою частоту

либо

частоту,

меньшую этой в целое число раз.

Такие

режимы называются режимами принудительной син-

хронизации на основной частоте либо, соответственно, на часто-

те субгармоник.

Возможен и режим совместного существования вынужденных

колебаний

и автоколебаний, т. е. режим биений. Исследование

16.4]

ОБЩИЕ

СВОЙСТВА ПРОЦЕССОВ

255

всех возможных режимов нелинейной системы

произвольной

линейной

частью представляет собой

настоящее время нераз-

решимую

задачу.

16.4. Общие свойства процессов

Выясним некоторые общие свойства процессов

нелинейных

системах. Рассмотрим сначала нелинейные системы

при

отсут-

ствии насыщения нелинейных

эле-

ментов.

этом

случае

(рис. 16.3)

функция

Ф(х),

определяющая

нелинейность,

как

правило, может

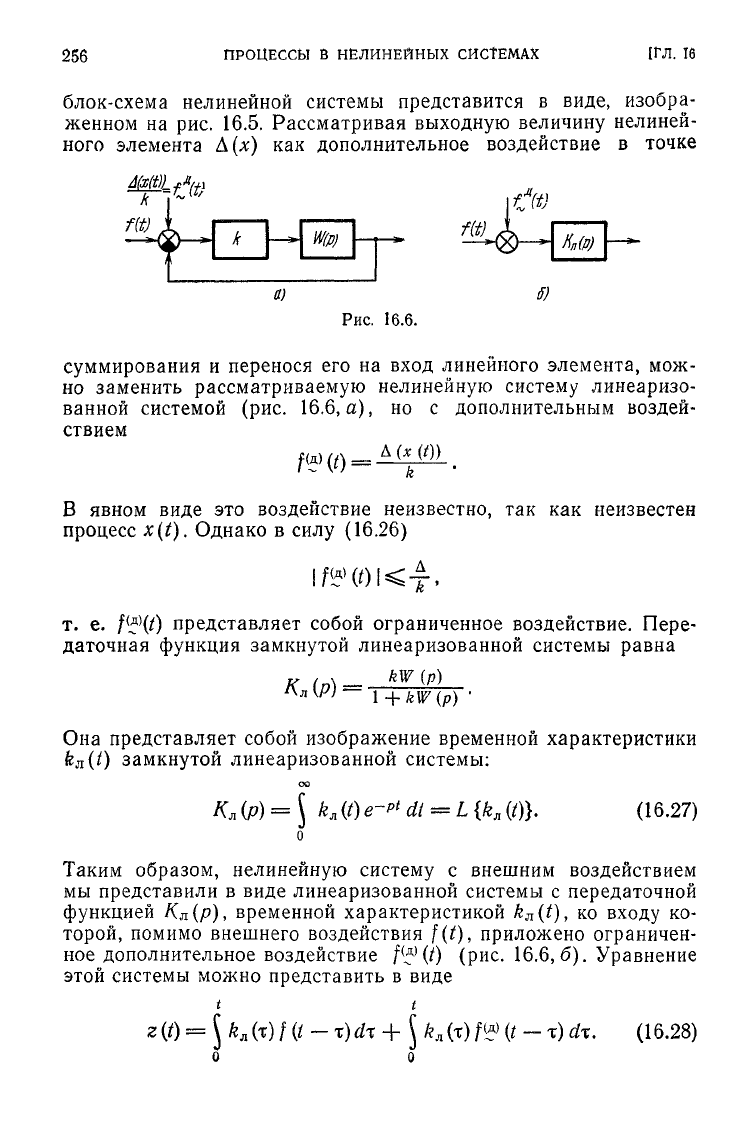
быть задана соотношением

(16.25)

где

Д (х)

0</г<оо,

Д =

const

< оо,

Рис.

16.3

(16.26)

Для нелинейностей этого типа

статический

k^(x)

дифферен-

циальный

£<#(*)

коэффициенты линеаризации удовлетворяют

условиям

lim

{c)

(x)=

lim

—~=

k>0,

lim

d<b

(x)

=k>0.

lim

Согласно

(16.25)

нелинейный элемент

при

отсутствии насыщения

Рис.

16.4.

Рис.

16.5.

может быть представлен

виде линейного элемента

нелиней-

ного элемента

насыщением, обладающего ограниченной

по аб-

солютной величине характеристикой

Д(#)

(рис.

16.4). Поэтому

256

ПРОЦЕССЫ

НЕЛИНЕЙНЫХ

СИСТЕМАХ

[ГЛ.

Тб

блок-схема нелинейной системы представится в виде, изобра-

женном

на рис. 16.5. Рассматривая выходную величину нелиней-

ного элемента А(х) как дополнительное воздействие в точке

fit)

б)

Рис.

16.6.

суммирования и перенося его на

вход

линейного

элемента, мож-

но

заменить рассматриваемую нелинейную систему линеаризо-

ванной

системой (рис. 16.6, а), но с дополнительным воздей-

ствием

В явном виде это воздействие неизвестно, так как неизвестен

процесс x(t). Однако в силу

(16.26)

т. е.

№(t)

представляет собой ограниченное воздействие. Пере-

даточная функция замкнутой линеаризованной системы равна

КГ

п\

Ал1/?)

~ 1 +

kW(p)

Она

представляет собой изображение временной характеристики

(()

замкнутой линеаризованной системы:

(Р)

(t)

{t)}.

(16.27)

Таким

образом, нелинейную систему с внешним воздействием

мы представили в виде линеаризованной системы с передаточной

функцией

/Сл(р),

временной характеристикой

(0>

ко

входу

ко-

торой,

помимо внешнего воздействия

/(/),

приложено ограничен-

ное

дополнительное воздействие

f№

(t) (рис.

16.6,6).

Уравнение

этой

системы можно представить в виде

Ь)

f((-x)dx+\k,

(т) f

<Д)

(t - т) dr. (16.28)

ОБЩИЕ

СВОЙСТВА ПРОЦЕССОВ

257

Обозначим выходную величину линеаризованной системы при от-

сутствии дополнительного воздействия через

(t).

Очевидно,

zAt)=\K{T)f{t-x)d%.

(16.29)

Отличие нелинейной системы

от

линеаризованной характери-

зуется разностью их выходных величин:

6г(/)

г(/)-г

(/).

(16.30)

Вычитая (16.29)

из

(16.28),

получаем

(t)

(т)

- т) dx. (16.31)

Оценивая

обе части

(16.31),

получим

| bz (t)

(т)

/<д>

т)

it.

(16.32)

Учитывая ограниченность дополнительного воздействия

пола-

гая

(16.32)

t =

оо, мы лишь усилим оценку,

тогда

(16.33)

Если

линеаризованная система устойчива,

только этот случай

имеет смысл рассматривать,

то

интеграл

правой части (16.33)

конечен,

мы получаем оценку изменения процесса нелинейной

системы по сравнению

линеаризованной.

Таким

образом,

максимальное

отклонение

процесса

нелинейной

системе

от

процесса

линеаризованной

системе

определяется

ве-

личиной

наибольшего

отличия

нелинейной

характеристи-

ки от

линейной,

коэффициентом

усиления

линейного

эле-

мента

k и

площадью

абсолютной

величины

временной

ха-

рактеристики

линеаризованной

системе.

Если

временная характеристика линеаризованной системы

неотрицательна,

, учитывая (16.27), получаем

оо оо

(т)

\к

(х) dx

(0)

, ^

(0)

•

(16.34)

Я 3

Цчпкич

258

ПРОЦЕССЫ

В НЕЛИНЕЙНЫХ СИСТЕМАХ

[ГЛ. та

Для астатических систем

(W(0)

oo)

в (16.34) имеет место

равенство и оценка (16 33) принимает особенно простой вид:

<4-

(16

)

-А

с.

16.7

Это наибольшее возмож-

ное отклонение.

Рассмотрим теперь не-

линейные

системы при на-

личии насыщения у нели-

нейных элементов. В этом

случае

(рис.

16.7) функ-

ция

Ф(х),

определяющая нелинейность в системе, является огра-

ниченной,

т. е.

|Ф(*)КФ««<°о.

(16.36)

Коэффициенты

линеаризации нелинейного элемента удовлетво-

ряют условиям

lim

№{x)^=

tim

-^-

(16.37)

(16.38)

Производя

оценку левой части уравнения нелинейной системы

(16.8) с учетом (16.36), получим

lim

{x)

=0.

(16.39)

Заменяя

сумму абсолютных значений воздействий их верхней

границей и замечая, что для устойчивой линейной части

\d%

(16.40)

получим

(16.41)

Отсюда следует, что в нелинейных системах

при наличии

насыщения

нелинейного

элемента

устойчи-

вой

линейной

частью

ограниченных

воздействиях

про-

цессы

всегда

ограничены.

ЗАДАЧИ

259

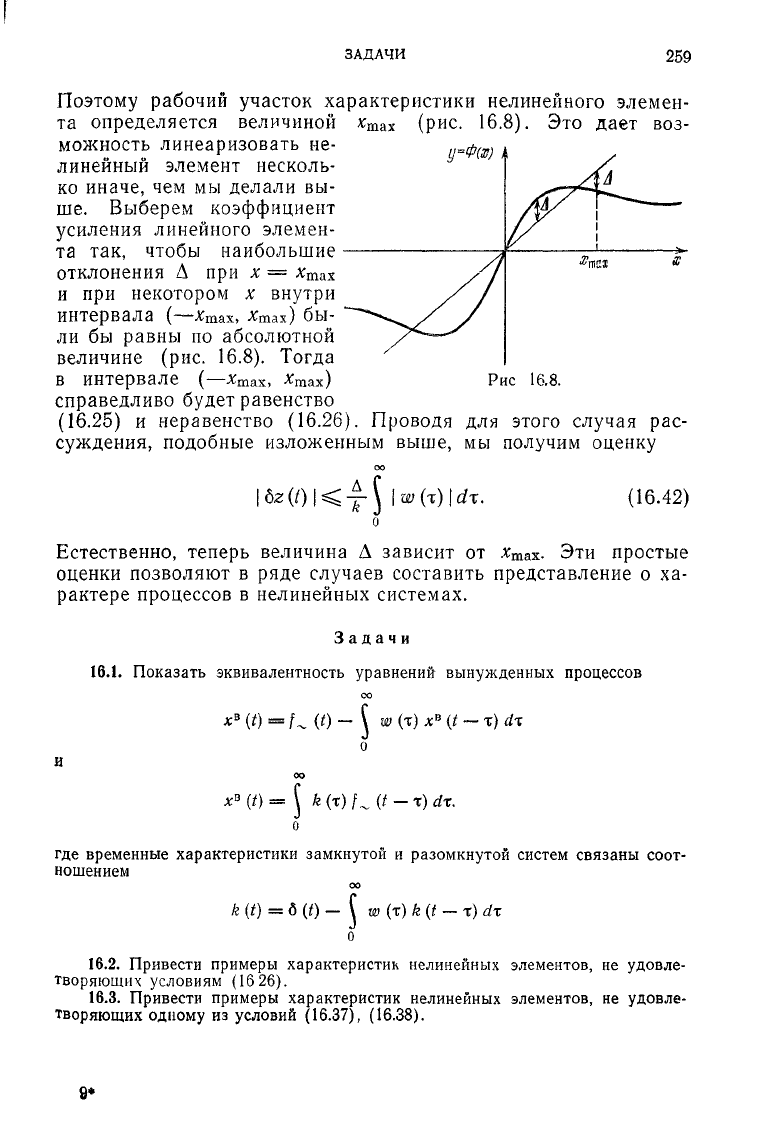
Поэтому рабочий участок характеристики нелинейного элемен-

та определяется величиной

можность линеаризовать не-

линейный

элемент несколь-

ко

иначе, чем мы делали вы-

ше.

Выберем коэффициент

усиления линейного элемен-

та так, чтобы наибольшие

отклонения

А при х =

л:

тах

при некотором х внутри

интервала

(—x

ax,

*тах)

бы-

ли

бы равны по абсолютной

величине (рис. 16.8). Тогда

интервале

(—х

тах

)

справедливо

будет

равенство

(16.25)

и неравенство (16.26). Проводя для этого случая рас-

суждения, подобные изложенным выше, мы получим оценку

(16.42)

*max

(рИС.

16.

8).

Это

дает

воз-

г*****-—•

max

Рис

16.8.

-f

\w{x)\dx.

Естественно, теперь величина А зависит от

д?

ах.

Эти простые

оценки

позволяют в ряде случаев составить представление о ха-

рактере процессов в нелинейных системах.

Задачи

16.1.

Показать эквивалентность уравнений вынужденных процессов

х*

(t)

f ^ (t) - [ w (x)

(t — т) dx

где временные характеристики замкнутой и разомкнутой систем связаны соот-

ношением

оо

(t) = б

[

w (х)

k(t-x)

16.2. Привести примеры характеристик нелинейных элементов, не

удовле-

творяющих условиям (16 26).

16.3. Привести примеры характеристик нелинейных элементов, не

удовле-

творяющих

одному из условий (16.37), (16.38).

Глава

УСТОЙЧИВОСТЬ

НЕЛИНЕЙНЫХ

СИСТЕМ

17.1.

Понятия

устойчивости

Состояние

равновесия, вынужденные процессы, автоколеба-

ния

могут

реально существовать лишь в том случае, когда они

устойчивы. Устойчивость этих режимов определяется характером

изменений

отклонений, вызванных приложением к системе убы-

вающих воздействий. Если эти отклонения стремятся с течением

времени к нулю, то соответствующие режимы устойчивы. Возни-

кающие отклонения представляют собой не что иное, как сво-

бодные процессы. Поэтому исследование устойчивости сводится

исследованию свободных процессов. В отличие от линейных

систем, в нелинейных системах свободный процесс существенно

зависит от рассматриваемых режимов. В нелинейных системах

возможны ситуации, в которых один режим устойчив,

тогда

как

другой

режим неустойчив. Так, при устойчивых автоколебаниях

часто состояние равновесия неустойчиво. Поэтому устойчивость

состояния

равновесия, вынужденных процессов и

автокочебаний

следует

рассматривать, вообще говоря, раздельно. В

эгой

главе

мы

будем

рассматривать устойчивость состояния равновесия и

устойчивость вынужденных процессов. Исследованию автоколе-

баний

и их устойчивости

будет

посвящена гл. 20.

Известны

различные понятия устойчивости положения равно-

весия

процессов. Нам удобно

будет

использовать понятия устой-

чивости, основанные на понятии свободного процесса. Рассмо-

трим

схему

нелинейной автоматической системы (рис. 17.1). Она

описывается уравнением (16.1). Для состояния равновесия

Ц()

(17.1)

уравнение свободного процесса принимает вид

(/) =

(0 -

(t -

т)

(T))

dr.

(17.2)

17.1]

понятия

УСТОЙЧИВОСТИ

261

Это уравнение описывает процессы в нелинейной системе, изо-

браженной на рис, 17.1, вызываемые убывающим воздействием

С).

Будем говорить, что состояние равновесия

z=~

устойчиво,

если для убывающих внешних воздействий

(/) таких, что

|^(/)|

ii<oo,

(17.3)

l(t)

свободный процесс

(t),

определяемый уравнением (17.2), огра-

ничен

и удовлетворяет условию

lim

(/)

(17.4)

Если

(17.3)

величина т] принимается достаточно малой, то со-

стояние

равновесия

устойчиво

«в

малом».

Если в

(17.3)

—

ко-

нечная

фиксированная вели-

чина,

то состояние равнове-

сия

устойчиво

«в

большом».

Если

же в

(17.3)

может

быть любой величиной, то

состояние равновесия

устой-

Рис.

17.1

чиво

«в

целом».

Наконец,

будем

говорить, что состояние равновесия

абсолютно

устойчиво,

если оно устойчиво в целом, но не для одной фиксированной ха-

рактеристики нелинейного элемента, а для некоторого семейства

этих характеристик, принадлежащих к какому-либо классу.

Для вынужденного процесса

(t),

определяемого уравне-

нием

МО

(17.5)

свободный процесс удовлетворяет уравнению, которое мы запи-

шем в такой форме:

(t)

(х

(т),

dx.

(17.6)

Здесь

(/), /) = Ф

(x«

(/) +

(/))

(x*

(/))

(17.7)

— преобразованная характеристика нелинейного элемента. В от-

личие от исходной характеристики нелинейного элемента систе-

мы,

преобразованная характеристика зависит от времени, т. е.

она

нестационарна, и это обстоятельство вносит свою специфику.

Для конкретного вынужденного процесса

(t)

все определения

устойчивости состояния равновесия остаются справедливыми для

устойчивости вынужденных процессов, если

левую

часть

нера-