Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

292

ИССЛЕДОВАНИЕ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ

[ГЛ. 18

положение равновесия абсолютно устойчиво при любых положи-

тельных статических коэффициентах линеаризации, т. е. при лю-

бых характеристиках нелинейного элемента, принадлежащих

первому и третьему квадрантам (рис.

18.4,а).

Полагая в частот-

ном

неравенстве

(17.60)

= оо, получим

Г(/со)>0,

(18.5)

или,

в развернутой форме,

(18.6)

Условия

(18.5)

или (18.6), очевидно,

будут

выполнены, если

можно провести прямую Попова через начало координат и при

этом модифицированная частотная

характеристика

№

(/со)

= U

(со)

/o)V((o)

будет

расположена спра-

ва от этой прямой (рис. 18.6). Для

выполнения

указанных свойств ли-

нейная

часть системы должна быть

прежде всего минимально-фазовой,

т. е. все нули числителя и знамена-

теля должны быть левыми. Кроме

того, характеристика

№

(/со)

не мо-

жет проходить больше

двух

квад-

рантов,

так как неравенство

(18.5)

требует,

чтобы характеристика

9/0))

W(/co)

целиком лежала в правой полуплоскости.

Условие

(18.5)

заведомо

будет

выполнено, если при мини-

мальной фазовости системы разность степеней числителя и зна-

менателя

W(](o)

меньше

двух,

т. е.

—т<2.

Обычно для

реальных систем, линейная часть которых состоит из типовых

звеньев, степень числителя меньше или равна степени знаме-

нателя,

т^п.

Условие

(18.5)

будет

выполнено при п = т или

при

п—-т=1.

В первом

случае

суммарное изменение фазы

частотной характеристики линейной системы равно нулю,

ТС

во втором

случае

—j".

соответствии с расположением

корней

числителя и знаменателя при изменении со от 0 до оо

частотная характеристика

Рис.

18.6.

при

я~Ш1=2

может зайти на высоких частотах в третий

квадрант, однако основная часть

W(/со)

будет

лежать в четвер-

том квадранте. В этом

случае

всегда можно подобрать такое

д,

18.2] ПОЛОЖИТЕЛЬНЫЕ

КОЭФФИЦИЕНТЫ

ЛИНЕАРИЗАЦИИ 293

что характеристика

целиком

будет

лежать в правой полуплоскости.

При п — т = 2

абсолютной

устойчивостью

секторе

(О,

оо)

обладают

системы,

линейные

части

которых

имеют

нули

полюсы

левой

полуплоскости,

ограниченной

бис-

сектрисами

второго

третьего

квадрантов.

Это условие обеспечивает монотонность изменения фазы ча-

стотной характеристики. Кроме того, если нули и полюсы

W(p)

удовлетворяют определенным условиям чередования, например,

если для

(

(PIP

1)(Р2Р+

•-•

(9пР+

УР)

(Т

+ I)

(Т

+ 1) ...

(Т

+ 1)

эти

условия чередования имеют вид

>р

>Г

>р

...

/z-m=l,

(18.7)

то частотная характеристика

W(j&)

целиком лежит в четвертом

квадранте. При п — m = 2 любой пропуск р в последовательно-

сти (18.7) можно скомпенсировать с помощью q так, что харак-

теристика (1 + fl

/co)U^(/co)

будет

целиком лежать в четвертом

квадранте. Аналогичные условия можно получить и для систем,

передаточная функция которых содержит комплексные, мнимые

нулевые полюсы.

Пример.

Пусть линейная часть системы имеет передаточную функцию

вида

де

т\

= а,

ЬТ

Ь.

Частотная характеристика такой системы изображена

на

рис. 18.7. Модифицированная частотная харак-

„,.

теристика, соответствующая ей, равна

1-асо

u (/С0)

1асо

6ю

а©

)

Ьсо

(1 -

аю

)

Ь®

Т^м

(/со) отличается от

W(/со)

лишь изменением

масштаба ординат в со раз. Так как со ^ 0, то

при

любом таком изменении

W(j®)

всегда через

начало координат можно провести прямую так,

чтобы эта характеристика лежала справа от нее.

А это значит, что состояние равновесия этой

нелинейной

системы

будет

абсолютно устойчивым

при

любом положительном коэффициенте статической линеаризации

№°)(х),

т. е. при любой характеристике нелинейного элемента, расположенной в пер-

вом и третьем

квадрантах.

294

ИССЛЕДОВАНИЕ

АБСОЛЮТНОЙ УСТОЙЧИВОСТИ [ГЛ.

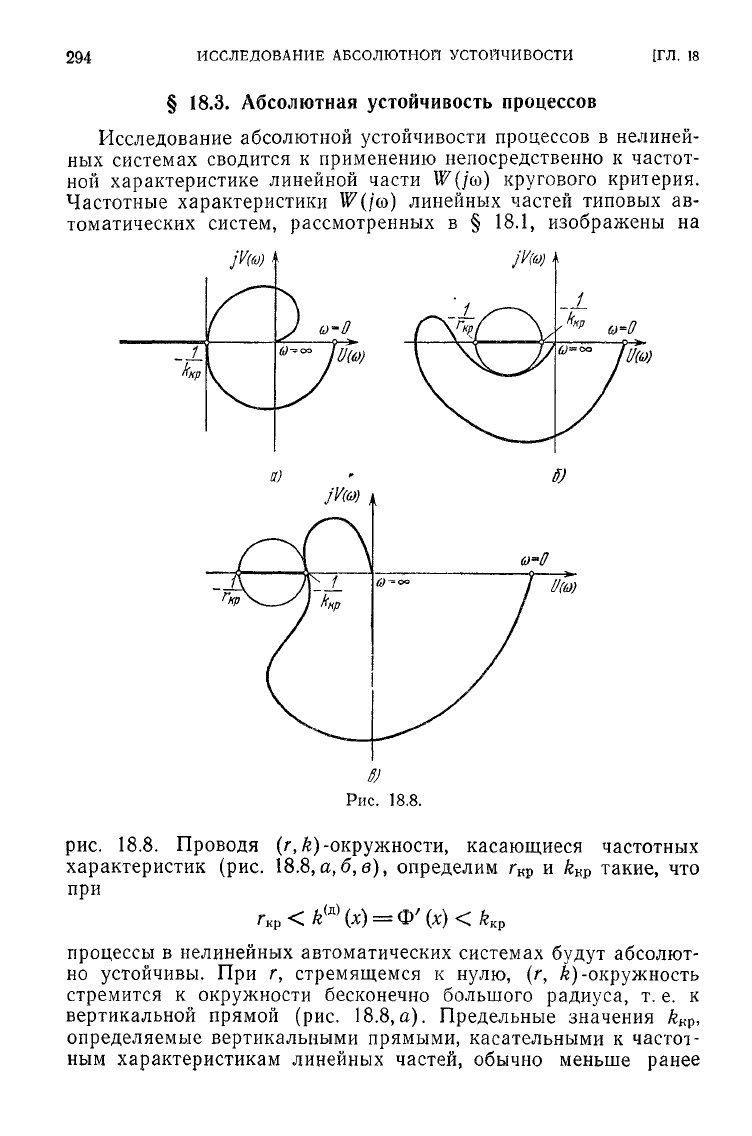
18.3. Абсолютная устойчивость процессов

Исследование абсолютной устойчивости процессов в нелиней-

ных системах сводится к применению непосредственно к частот-

ной

характеристике линейной части

W(j(o)

кругового критерия.

Частотные характеристики

W(jco)

линейных частей типовых ав-

томатических систем, рассмотренных в § 18.1, изображены на

"хр

Рис.

18.8.

рис.

18.8. Проводя

(г,

k) -окружности, касающиеся частотных

характеристик (рис.

18.8,а,б,в),

определим

кр

такие, что

при

процессы в нелинейных автоматических системах

будут

абсолют-

но

устойчивы. При

г,

стремящемся к нулю,

(г,

k) -окружность

стремится к окружности бесконечно большого

радиуса,

т. е. к

вертикальной прямой (рис. 18.8, а). Предельные значения

кр

определяемые вертикальными прямыми, касательными к частот-

ным

характеристикам линейных частей, обычно меньше ранее

ЗАДАЧИ

295

определенных предельных значений. Во

всех

рассмотренных слу-

чаях

&гр,

т. е. область абсолютной устойчивости процессов

уже области абсолютной устойчивости положения равновесия.

Эти области

будут

совпадать

между

собой и

будет

равно

гр

когда вер-

тикальная

прямая (рис. 18.8, а) каса-

ется

W(j(u)

в точке ее пересечения с

действительной осью или когда

(г,

k) •

окружность касается

Щ/со)

в точках ее

пересечения с действительной осью

(рис.

18.8, в). В этих случаях круговой

критерий

является необходимым и до-

статочным.

кр

может иметь значе-

ния,

большие

гр

в том случае, ко-

гда

k№

(х) =

Ф'(х)

изменяется в не-

больших пределах, т. е. нелинейная

функция

Ф(л;)

мало отличается от ли-

нейной.

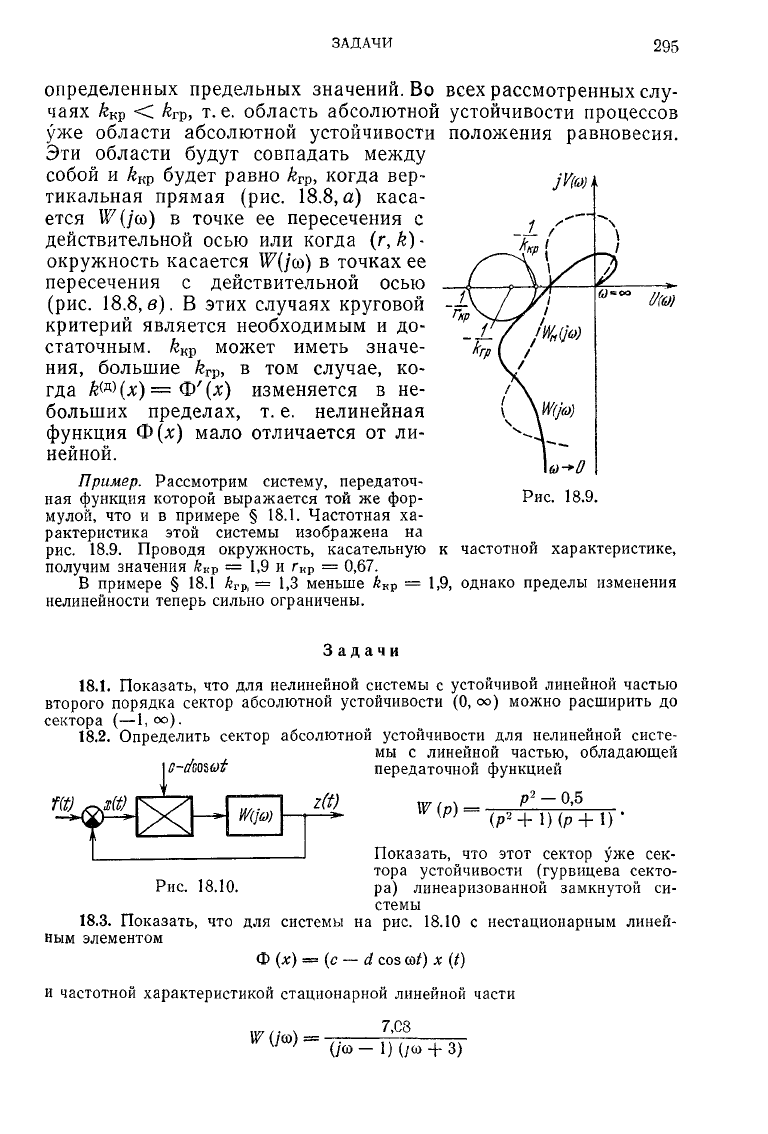
Пример.

Рассмотрим систему, передаточ-

ная

функция которой выражается той же фор-

мулой, что и в примере § 18.1. Частотная ха-

рактеристика этой системы изображена на

рис.

18.9. Проводя окружность, касательную к частотной характеристике,

получим значения

1,9

кр

= 0,67.

В примере § 18.1

ГР|

= 1,3 меньше

= 1,9, однако пределы изменения

нелинейности

теперь сильно ограничены.

Задачи

18.1.

Показать, что для нелинейной системы с устойчивой линейной частью

второго порядка сектор абсолютной устойчивости (0, оо) можно расширить до

сектора

(—1,

оо).

18.2. Определить сектор абсолютной устойчивости для нелинейной систе-

мы с линейной частью, обладающей

передаточной функцией

fit)

lit)

— 0,5

Показать,

что этот сектор уже сек-

тора устойчивости (гурвицева секто-

Рис.

18.10.

ра)

линеаризованной замкнутой си-

стемы

18.3. Показать, что для системы на рис. 18.10 с нестационарным линей-

ным

элементом

(х) = (с — d cos

со/)

х (t)

частотной характеристикой стационарной линейной части

ОЯ

296 ИССЛЕДОВАНИЕ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ

{ГЛ. 18

условия абсолютной устойчивости имеют вид

3,5

—d

cos

(at

< 10,7.

18.4. Применить геометрическую интерпретацию условия устойчивости за-

дачи 17.2 к нелинейной системе, частотная характеристика линейной части ко-

торой равна

(/со-1)

(/со+

4)'

18.5.

Показать

}

что если линейная часть системы имеет передаточную

функцию

bop

bip

(p)

—-z—;

5—;

;

~\-

Q\P

Иг

&2P

(Ь2П\

—

Ьопо)

^0,

то условия абсолютной устойчивости нелинейной системы

r<<k

совпадают с условиями устойчивости статически линеаризованной системы.

Глава

ОЦЕНКИ

КАЧЕСТВА

СВОБОДНЫХ

ПРОЦЕССОВ

19.1.

Виды

оценок

Свободный процесс в нелинейных автоматических системах

характеризует переход от некоторого начального состояния к

устойчивому состоянию равновесия или устойчивому вынужден-

ному режиму. Оценками свободного процесса могут служить та-

кие

показатели качества, как

мера

быстродействия

или

степень

устойчивости

квадратическое

интегральное

отклонение.

Для линейных систем эти оценки, как было показано в § 12.1

§ 13.2, могут быть найдены точно. Для нелинейных систем та-

кая

возможность исключена и приходится довольствоваться уста-

новлением

границ, внутри которых могут находиться эти оценки.

19.2.

Оценка

меры

быстродействия

нелинейных

систем

Будем говорить, что

быстродействие

или

степень

устойчиво-

сти

нелинейной

системы

не меньше заданной

go,

если

limx

(0e

= 0. (19.1)

t->oo

Равенство (19.1) означает, что свободный процесс

(t)

с ро-

стом t убывает быстрее затухающей экспоненты

е~^.

Уравне-

ние

свободного процесса, как было показано ранее, может быть

представлено в виде

(/)

= fr

(/)

о;

- т) Ф

{х

(т)) dr. (19.2)

Чтобы определить условия, при которых быстродействие нели-

нейной

системы не меньше

умножим левую и правую части

уравнения (19.2) на

е^,

тогда

• (t)

(t)

- \

т)

е^»

С-«)ф

(- ^/ )

dr.

298

ОЦЕНКИ

КАЧЕСТВА СВОБОДНЫХ ПРОЦЕССОВ [ГЛ. 19

Введем новые обозначения:

w{t) =

**•', ф

(jg

Тогда преобразованное уравнение запишется так:

(/)

(t -

т)

(т),

т)

dr.

Это уравнение можно рассматривать как уравнение некоторой

нелинейной

системы с нестационарной характеристикой нелиней-

ного элемента

Ф(£

т). Назовем эту нелинейную систему пре-

образованной.

Если

преобразованная нелинейная система абсолютно устой-

чива,

то

Нт

(0 =

lim

(t)

= О

и,

значит, по определению

(19.1)

быстродействие исходной не-

линейной

системы

будет

не меньше

Таким образом,

определение

быстродействия

нелинейной

системы

сводится

определению

абсолютной

устойчивости

состояния

равно-

весия

преобразованной

нелинейной

системы.

Покажем,

что к преобразованной нелинейной системе с не-

стационарной

нелинейной характеристикой применимы частот-

ные

критерии устойчивости, установленные в гл. 17. Доказа-

тельство справедливости критерия, приведенное в гл. 17, непо-

средственно можно перенести на преобразованную систему

том

случае, если для нестационарного нелинейного элемента спра-

ведливо неравенство

(t)

Ф(х

(т),

x)dx

(т)>0.

(19.3)

Поскольку

обратная функция х(х) может быть не однозначной,

то написанный интеграл понимается как сумма интегралов по

интервалам монотонности х(х). Для функции Ф

(х

(т), т)

(

)

\ ф

(

)

f—-j^.—

при 0 < —— <

справедливость неравен-

ства легко устанавливается. В самом деле,

19 2] ОЦЕНКА

.МЕРЫ

БЫСТРОДЕЙСТВИЯ НЕЛИНЕЙНЫХ СИСТЕМ 29Э

Поскольку

то неравенство

(19.3)

справедливо при любом т ^ 0. Поэтому

преобразованной системе применимы частотные критерии

устойчивости, установленные в гл. 17.

Временная характеристика линейной части преобразованной

системы равна

xs)

(t)

= w (t)

е^.

Следовательно, частотная характеристика преобразованной си-

стемы по определению

будет

равна

со

сю

(/со) =

w(t)

e-№

dt=\w

(t)

e-^-W

*dt

(/со -

go).

Назовем

ее для краткости

смещенной

частотной

характеристи-

кой

линейной

части.

Условию принадлежности нестационарной

нелинейной

характеристики

Ф(£

t) преобразованной системы

сектору

(г,

ko)

эквивалентно

условие принадлежности стационарной нелинейной

характеристики

Ф(х

)

исходной системы тому же сектору

(r,ko)

Введем понятие

модифицированной

смещенной

частотной

ха-

рактеристики

^м(/©-go)

£/(©,

УУ(со,

Ь,),

где

t/(©,

go) =

Rer(/co-go),

(со,

)

©Imry<o-go).

Тогда, заменяя в формулировках частотных критериев частот-

ные

характеристики на смещенные частотные характеристики,

мы получим критерии быстродействия, т. е. критерии, обеспечи-

вающие быстродействие нелинейной системы, не меньшее чем

Таким

образом, мы приходим к следующим формулировкам ча-

стотных критериев быстродействия.

300

ОЦЕНКИ

КАЧЕСТВА

СВОБОДНЫХ

ПРОЦЕССОВ

[ГЛ.

Частотный

критерий быстродействия 1 (линеарный крите-

рий быстродействия). Нелинейная система с устойчивой

линейной

частью

характеристиками

нелинейного элемента

(х),

принадлежащими сектору (0,

будет обладать

быстродействием,

не меньшим

если модифицированная

смещенная

частотная

характеристика

(/co

—

)

не

пере-

секает

(q,

)-прямую.

Частотный

критерий быстродействия II (параболический

критерий

быстродействия).

Нелинейная система с устой-

чивой,

или нейтральной линейной частью и характе-

ристиками

нелинейного элемента

Ф(х),

принадлежащими

сектору

(г,

будет обладать

быстродействием,

не

.мень-

шим

если модифицированная смещенная

частотная

ха-

рактеристика

(/co

—

£о)

не

пересекает

г)-параболу.

Таким

образом,

исследование

быстродействия

нелинейных

си-

стем

сведено

применению

частотных

критериев

абсолютной

устойчивости

положения

равновесия,

но в

которых

фигурирует,

вместо

модифицированной

частотной

характеристики,

модифици-

рованная

смещенная

частотная

характеристика.

Напомним,

что

принадлежность

характеристики

нелинейного

элемента

Ф(х)

сектору

(г,

ko)

означает

принадлежность

коэффициента

статиче-

ской

линеаризации

k^(x)

полосе

(г, ko).

Если

прямая

(q,

ko)

или

парабола

(q,

могуг

быть

проведены

так, чтобы они

касались

смещенной

модифицированной

частотной

характеристи-

ки

(j<u

—

Ео)

точке

пересечения

ее с

вещественной

осью и

(j(o

—

|о)

была

расположена

справа,

то (см. §

18.1)

быстро-

действие

границы

устойчивости

преобразованных

нелинейной

соответствующей

линеаризованной

системы

будут

совпадать,

следовательно,

нелинейной

системе

будет то же

быстродей-

ствие

|о,

что и в соответствующей

линеаризованной

системе.

общем

случае быстродействие нелинейной системы не

может

превосходить максимального быстродействия соот-

ветствующей

линеаризованной системы.

Для

нелинейных

систем

нестационарной

частотной

характе-

ристикой

Ф(х

оценка

быстродействия

осуществляется на

основе

частотного

критерия быстродействия III (кругового кри-

терия

быстродействия).

Быстродействие

нелинейной системы с нестационарной ха-

рактеристикой

нелинейного элемента

Ф(х

,1),

принадле-

жащей при всех t сектору

(г,

k),

будет не меньше

go,

если

смещенная

частотная

характеристика

W(jсо

—

£о),

не пе-

ресекая

(ko,

r)-окружности,

охватывает

ее в положитель-

ном направлении

sJ2

раз,

где

—

индекс

неустойчивости

линейной

части

передаточной функции.

19?]

ОЦЕНКА

КВАДРАТИЧЕСКОГО

ИНТЕГРАЛЬНОГО

ОТКЛОНЕНИЯ

301

Этот частотный критерий быстродействия

III

позволяет

оце-

нить скорость протекания процессов

нелинейной системе

с не-

стационарной характеристикой.

Пример.

Рассмотрим систему, частотная характеристика линейной части

которой равна

(2/©+1)(/ю

1)(0,5/©+1)'

Зададимся быстродействием

0,5.

Тогда смещенная частотная

характери-

стика, получаемая заменой

/со

на

/со

—

0,5,

запишется

так:

(/со

0,5)

2/со (/со

0,5)

(0,E]^+~0jET"'

а соответствующая модифицированная характеристика

(рис.

19.1)—так:

„

1 .

0,375

О,5со

Wm l/0 u>Dj

__ ^^

+ 1

0)2

;

0,5со

1,25ю

0,28

Проводя

касательную

модифицированной смещенной частотной характеристике,

Рис.

19.1.

определяем граничное значение статического коэффициента линеаризации:

Нелинейная

система

будет

обладать быстродействием,

не

меньшим

чем

0,5,

если

19.3. Оценка квадратического

интегрального

отклонения

Квадратические

интегральные отклонения, вызываемые сво-

бодным процессом, можно определить как