Цыпкин Я.З Основы теории автоматических систем
Подождите немного. Документ загружается.


302
ОЦЕНКИ
КАЧЕСТВА СВОБОДНЫХ ПРОЦЕССОВ [ГЛ. 19
ИЛИ
Для оценки /Ф и
1
Х
воспользуемся неравенством (17.22), которое
представляет собой следствие выполнения условия устойчивости
Fi
(t) ^
0.
Полагая в нем q = 0, получим
р
=
J
|>
(6)
-
1Ф
(х
с
(6))]
Ф
(*
с
(6))
сЮ
<
J
fr
(0)
Ф
(х
с
(0))
dQ.
(19.4)
о
о
При
/~^оо
из оценки для р получаем после очевидных преоб-
разований
Ф
2
(;
о
о
Так
как характеристика нелинейного элемента принадлежит сек-
тору (0,
&о),
то максимальный статический коэффициент усиле-
ния
kmax
удовлетворяет неравенству
Следовательно,
(19.5)
Правую же часть неравенства
(19.4)
на основании неравенства
Коши
— Буняковского (приложение 4) преобразуем к виду
1/2 , оо
ч
1/2
(19.6)
e
.
Принимая
во внимание обозначение для /
ф
и неравенства (19.5),
(19.6),
получим
1/2

§
19.3]
ОЦЕНКА КВАДРАТИЧЕСКОГО ИНТЕГРАЛЬНОГО ОТКЛОНЕНИЯ
303
или,
после возведения в квадрат и элементарных преобразо-
ваний,
\2
м
Поскольку
согласно теореме Парсеваля
где /^ (/со) — спектральная функция
j>(0>
то оценка /Ф может
быть также представлена в виде
Замечая,
что
получаем
оо оо
/Ф
= \ Ф
2
(х
с
(9))
dQ
>
(^]
n
)
2
J
х
2
(9)
dQ
=
{k%.
n
fl
x
.
(19.8)
0
0
И
следовательно, из
(19,7)
с учетом
(19.8)
получим
Если
характеристика нелинейного элемента Ф (х) принадлежит
не
сектору (0,
k
Q
),
a (r,
k
0
),
то в полученных выше оценках I
х
следует
заменить
k
Q
на
k
Q
—
г,
k^\
x
на
/г^
х
—
г
и fe^
}n
на
^min~~"
r
-
Таким образом, в общем случае
будем
иметь
где
Пример.
Рассмотрим нелинейную систему, абсолютная устойчивость ко-
торой
была исследована в примере § 18.1. Пусть характеристики нелинейного
элемента
таковы, что
^
ax
~'-0fi)
kf£\
n
= 0,3;
&
0
=1,3.
Граничное значение

304
ОЦЕНКИ
КАЧЕСТВА СВОБОДНЫХ ПРОЦЕССОВ [ГЛ
14
коэффициента
статической линеаризации, как было найдено ранее, равно
k
0
=
&
гр
=
1,3. Подставляя эти значения в формулу (19.7), получим
00
1
о2
,
п
R
2
Лф
^ (1,3
-0,6)
2
о
или
Аналогично
будем
иметь
или
о
Оценка
I
х
,
естественно, более грубая, чем /
ф
Оценка
(19.9), как и приведенные выше оценки, пригодна
для любых свободных процессов, имеющих место в нелинейных
автоматических системах, для любых характеристик, принадле-
жащих
углу
(г,
ko)
или (0,
&о),
и любых частотных характери-
стик
линейной части, при которых нелинейная система абсолют-
но
устойчива. Столь малая информация о характеристиках нели-
нейной
системы, естественно,
требует
определенной платы, и эта
плата состоит в том, что для конкретных характеристик оценки
процессов
могут
получиться завышенными.
Задачи
19.1.
Начертить качественный вид смещенной частотной характеристики
Г
(/© — go) при
бо-О;
<№;
I;
2 и
W
(/со)
- ^
19.2. Показать, что быстродействие
§о
= 0,5 системы в задаче 18 3 дости-
гается при с = 25 и d = 5
19.3. Найти опенку квадратического интегрального отклонения для си-
стемы на рис. 18.10 при условии, что

Глава
20
ПЕРИОДИЧЕСКИЕ ПРОЦЕССЫ
§
20.1,
Понятие
о
периодических
процессах
Характерными периодическими процессами в нелинейных си-
стемах являются
автоколебания.
Автоколебания возможны лишь
тогда,
когда нелинейная система не может быть абсолютно
устойчивой. Поэтому задача исследования возможности суще-
ствования автоколебаний и их свойств возникает, если критерии
абсолютной устойчивости положения равновесия не выпол-
няются.
Установление факта существования автоколебаний и ис-
следование зависимости их частоты и амплитуды от параметров
линейной
части и характеристики нелинейного элемента позво-
ляют выяснить возможности устранения автоколебаний или
уменьшения их амплитуды до необходимой величины
тогда,
когда автоколебания нежелательны, либо наметить пути
уста-
новления
нужной частоты и амплитуды
тогда,
когда автоколеба-
ния
являются нормальным, рабочим режимом. Весьма важным
является выяснение поведения нелинейной автоматической си-
стемы при внешнем периодическом или гармоническом воздей-
ствии.
Такое внешнее воздействие может устранить автоколеба-
ния,
навязав системе свою
частоту
либо
частоту,
в целое число
раз меньшую.
Точное решение подобных нелинейных задач возможно для
очень ограниченного класса характеристик нелинейных элемен-
тов, а именно кусочно-линейных и, в частности, релейных авто-
матических систем. Поэтому в общем
случае
широко исполь-
зуются различные приближенные методы исследования автоко-
лебаний и вынужденных колебаний. Среди них выделяется своей
простотой, наглядностью и физичностью метод, основанный на
гармонической линеаризации.
При
исследовании абсолютной устойчивости состояния равно-
весия
и процессов мы использовали статическую и дифференци-
альную линеаризации. Гармоническая линеаризация специально
приспособлена для исследования периодических процессов в не-
линейных
системах.

306
ПЕРИОДИЧЕСКИЕ
ПРОЦЕССЫ [ГЛ. 20
§
20.2.
Гармонический баланс для автоколебаний
Как
было показано в гл. 16, возможные автоколебания опи-
сываются нелинейным уравнением вида
оо
х
а
(/)==-
J
w
(т)
Ф
(х
а
(t
-
х))
dr.
(20.1)
о
Точное решение этого уравнения при произвольной характери-
стике нелинейного элемента невозможно. Для приближенного
решения его воспользуемся понятием гармонической линеариза-
ции.
Будем искать решение нелинейного уравнения
(20.1)
в виде
x
a
(t)
=
Л
sin
со/
или,
в комплексной форме,
la
(f)
=
А
е
т.
(20.2)
Воспользуемся гармонической линеаризацией. При этом урав-
нение
нелинейного элемента у = Ф(х) заменяется на
g()
=
Ъ
г)
(Л)
1
а
(t) =
k^
(Л)
Ае№.
(20.3)
Подставляя
(20.2)
и
(20.3)
в уравнение (20.1), получим уравне-
ние
гармонически линеаризованной нелинейной системы:
оо
д
е
№
= —
^
w
(х)
%^
(Л)
Ае*<*
{t
~
x)
dx,
о
или
= —
i\
w (т)
e"№
dx
\ ^
(Л)
Отсюда,
учитывая, что по определению частотной характери-
стики
оо
jj
w
(x)
e-№
dx
=
W
(/со),
о
получаем основное соотношение:
l
=
-W(fa)%M(A).
(20.4)
Это соотношение имеет ясный физический смысл. Разомкнем не-
линейную систему
(рис.
20.1, а) на
входе
нелинейного элемента
и
приложим ко
входу
разомкнутой системы гармоническое воз-
действие амплитуды А и частоты со
(рис.
20.1,6).
На
выходе
не-
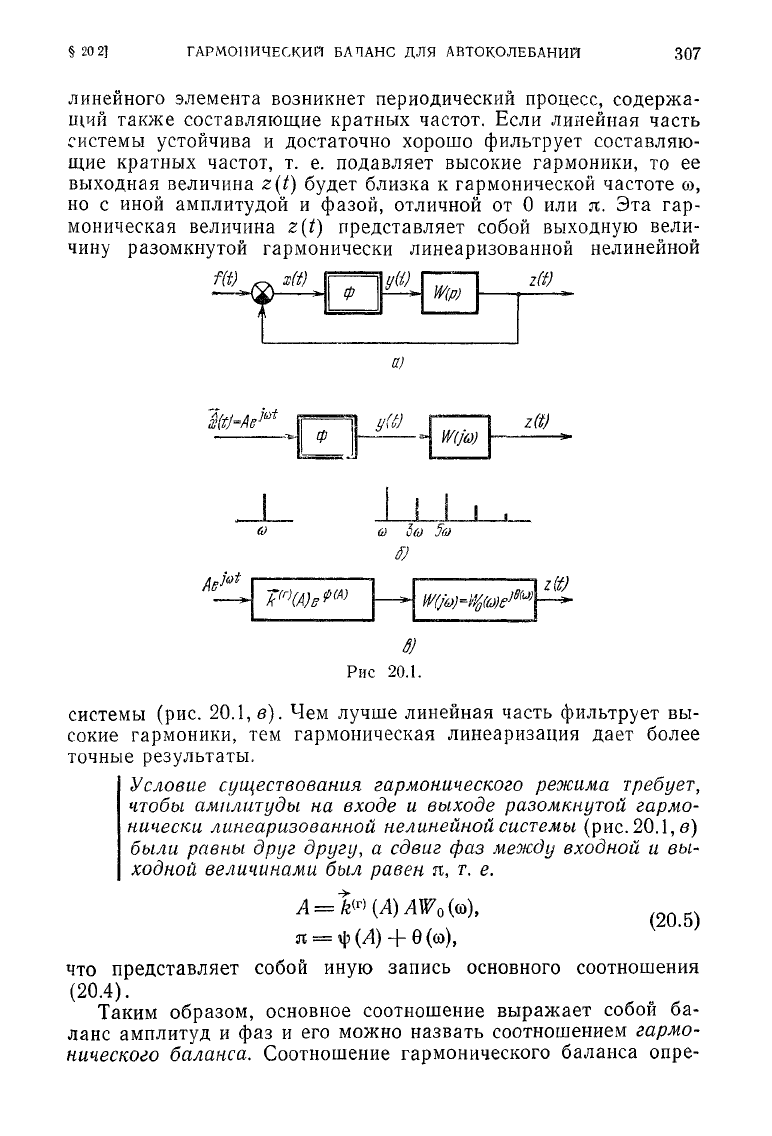
§
20
2]
ГАРМОНИЧЕСКИЙ
БЛПАНС
ДЛЯ АВТОКОЛЕБАНИЙ
307
линейного
элемента возникнет периодический процесс, содержа-
щий
также составляющие кратных частот. Если линейная часть
системы устойчива и достаточно хорошо фильтрует составляю-
щие
кратных частот, т. е. подавляет высокие гармоники, то ее
выходная величина z(t)
будет
близка к гармонической частоте со,
но
с иной амплитудой и фазой, отличной от 0 или я. Эта гар-
моническая
величина z(t) представляет собой выходную вели-
чину разомкнутой гармонически линеаризованной нелинейной
f(t)
Щр)
z(t)
а)
Wlja)
z(t)
п)
J
ff)
(0
JO
lit)
в)
Рис 20.1.
системы (рис. 20.1, в). Чем лучше линейная часть фильтрует вы-
сокие
гармоники, тем гармоническая линеаризация дает более
точные результаты,
Условие
существования
гармонического
режима
требует,
чтобы
амплитуды
на
входе
и
выходе
разомкнутой
гармо-
нически
линеаризованной
нелинейной
системы
(рис. 20.1, в)
были
равны
друг
другу,
а
сдвиг
фаз
между
входной
и вы-
ходной
величинами был
равен
я,
т. е.
_
h
(20.5)
что представляет собой иную запись основного соотношения
(20.4).
Таким
образом, основное соотношение выражает собой ба-
ланс амплитуд и фаз и его можно назвать соотношением
гармо-
нического
баланса.
Соотношение гармонического баланса
опре-

308
ПЕРИОДИЧЕСКИЕ ПРОЦЕССЫ [ГЛ.
20
деляет амплитуду
Л
а
и
частоту
со
а
возможных автоколебаний.
Хотя физическая интерпретация соотношения гармонического
баланса относится к
системам,
в которых линейная часть устой-
чива, само по себе соотношение гармонического баланса спра-
ведливо в любых
случаях.
Амплитуда
А
а
и частота
со
а
являются
решениями
алгебраических уравнений (20.5). Но эти алгебраи-
ческие уравнения выражают то обстоятельство, что гармониче-
ски
линеаризованная система находится на границе устойчиво-
сти.
Отсюда
следует,
что
условие
существования
автоколебаний
требует
такого
из-
менения
коэффициента
гармонической
линеаризации
за
счет
изменения
амплитуды
А и
частоты
со, при
котором
гармонически
линеаризованная
нелинейная
система
вы-
водится
на
границу
устойчивости.
§
20.3.
Определение
амплитуды
и
частоты
автоколебаний
Определение амплитуды и частоты автоколебаний и исследо-
вание
их зависимости от параметров линейной части системы сво-
дится к изучению поведения гармонически линеаризованной си-
стемы на границе устойчивости. Для этой цели можно исполь-
зовать частотный или алгебраический критерий устойчивости
линейных
систем, находя из него условия вывода системы на гра-
ницу
устойчивости. Часто можно
использовать уже готовые резуль-
таты исследования устойчивости
соответствующих линейных си-
стем, представленные в виде об-
ластей и границ устойчивости.
Рассмотрим вначале непосред-
ственное применение соотноше-
ния
гармонического баланса
(20.4). Запишем его в форме
J\
WQco)
(A)
(20.6)
Рис. 20.2.
Если
на комплексной плоскости
изобразить частотную характери-
стику линейной части
W(/co)
и отрицательный обратный
коэффи-
(рис.20.2),то
точ-
(А)
циент
гармонической линеаризации
—
ка
пересечения
их
определит частоту
со
а
/по
оцифровке
—.
и
амплитуду
А ( по
оцифровке
—
-$
]
Ч
k
{r)
(A)J
возможных автоколе-

.
20
3]
ОПРЕДЕЛЕНИЕ
АМПЛИТУДЫ И ЧАСТОТЫ АВТОКОЛЕБАНИЙ
309
баний.
Это построение очень
удобно
для исследования влияния
параметров нелинейной системы на
частоту
и
амплитуду
воз-
можных автоколебаний. Изменение параметров линейной части
приводит к деформации частотной характеристики
lF(/co),
а из-
менение
характеристики нелинейного элемента приводит к
изме-
нению
отрицательного обратного коэффициента гармоничес-
кой
линеаризации.
Отсутствие
точки пересечения
W(jay)
и
~-~—
(
рис
.
20.3) свиде-
/^^\W(](o)
к
(л)
тельствует
лишь о том, что ав-
токолебания искомой формы
отсутствуют.
Описанный выше
способ исследования был осно-
ван
на использовании частот-
ной
характеристики линейной
части и тесно связан с частот-
ным
критерием устойчивости
линейных
систем.
Возможен и иной способ ис-
следования, использующий ха-
рактеристическое уравнение и
тесно связанный с алгебраическими критериями устойчивости.
Для этой цели
введем
понятие
передаточной
функции
гармони-
чески
линеаризованного
нелинейного
элемента-.
fe(r>
(£,
л)
=
fe<
r)
{А)
-
ki
r)
(A)
-£
.
(20.7)
При
р = /со эта передаточная функция совпадает с коэффициен-
том гармонической линеаризации:
——
h^
(Л\
-
t?^
(Л\
. *
1Ь^
(А\
(00
R\
Рис.
20.3.
В отличие от коэффициента гармонической линеаризации /
передаточная функция гармонически линеаризованного нелиней-
ного элемента
&
(г)
(—,
ЛЬависит
не только от амплитуды,
ной
от частоты со автоколебаний. Передаточная функция разомкну-
той гармонически линеаризованной системы равна произведе-
нию
передаточных функций гармонически линеаризованного не-
линейного
элемента и передаточной функции линейной части
системы, т. е.
k
{T)
(-£-,
Л) W
(р)
=
[№
(Л)
-
k
{
?
(Л)
|-]
W
(р). (20.9)
Но
так как
р,
,

310
ПЕРИОДИЧЕСКИЕ
ПРОЦЕССЫ
[ГЛ 20
то,
суммируя знаменатель и числитель (20.9), получаем харак-
теристическое уравнение гармонически линеаризованной замкну-
той системы:
G
(£'
Л)
=
Q
(/>)
+
[kT
(Л)
-
kf
(А)
£]
Р (р)
=
0.
(20.10)
К
этому характеристическому уравнению
могут
быть применены
алгебраические критерии устойчивости.
Если
потребовать, чтобы гармонически линеаризованная си-
стема была на границе устойчивости, т.е. чтобы характеристиче-
ское уравнение
(20.10)
имело пару чисто мнимых корней, а
остальные все корни были левыми, то те значения А
и
со, при ко-
торых это имеет место, и определяют амплитуды и частоты воз-
можных автоколебаний. Особенно просто определение ампли-
туд и частот возможных автоколебаний в нелинейных системах
с однозначной характеристикой нелинейного элемента. В этом
случае
и,
значит, гармонический коэффициент линеаризации веществен:
Следовательно, —
1
совпадает с вещественной
fe(r)
(
д\
&(
г
)
(А)
осью (рис. 20.3). Граничная частота в этом
случае
определяется
полностью линейной частью
системы и не зависит от ха-
рактеристики нелинейного
krp
элемента. Она равна гранич-
ат"*
ной частоте линейной части
системы. Определяя на ос-
нове анализа устойчивости
линейной
системы любым
способом граничный
коэф-
фициент
усиления
&
гр
и при-
равнивая
его коэффициенту
усиления разомкнутой гар-
монически
линеаризованной системы
kj^
(Л),
находим уравне-
ние
относительно амплитуды возможных автоколебаний:
k
{
s
]
{A)
=
^.
(20.11)
Проще
всего уравнение
(20.11)
решается графически (рис. 20.4).
Изменение
параметров линейной части изменяет
k
TV
и
А
л
,
т. е.
правую часть уравнения
(20.11),
а изменение характеристики не-
Рис.
20.4.
§
20.3]
ОПРЕДЕЛЕНИЕ
АМПЛИТУДЫ И ЧАСТОТЫ АВТОКОЛЕБАНИЙ
311
линейного
элемента изменяет
левую
часть уравнения
(20.11).Та-
ким
образом, можно выяснить влияние параметров и характери-
стик
системы на параметры автоколебаний. Особенно удобно
для этой цели использовать границы устойчивости линейных си-
стем, представляющих собой зависимость
k
TV
от параметров си-
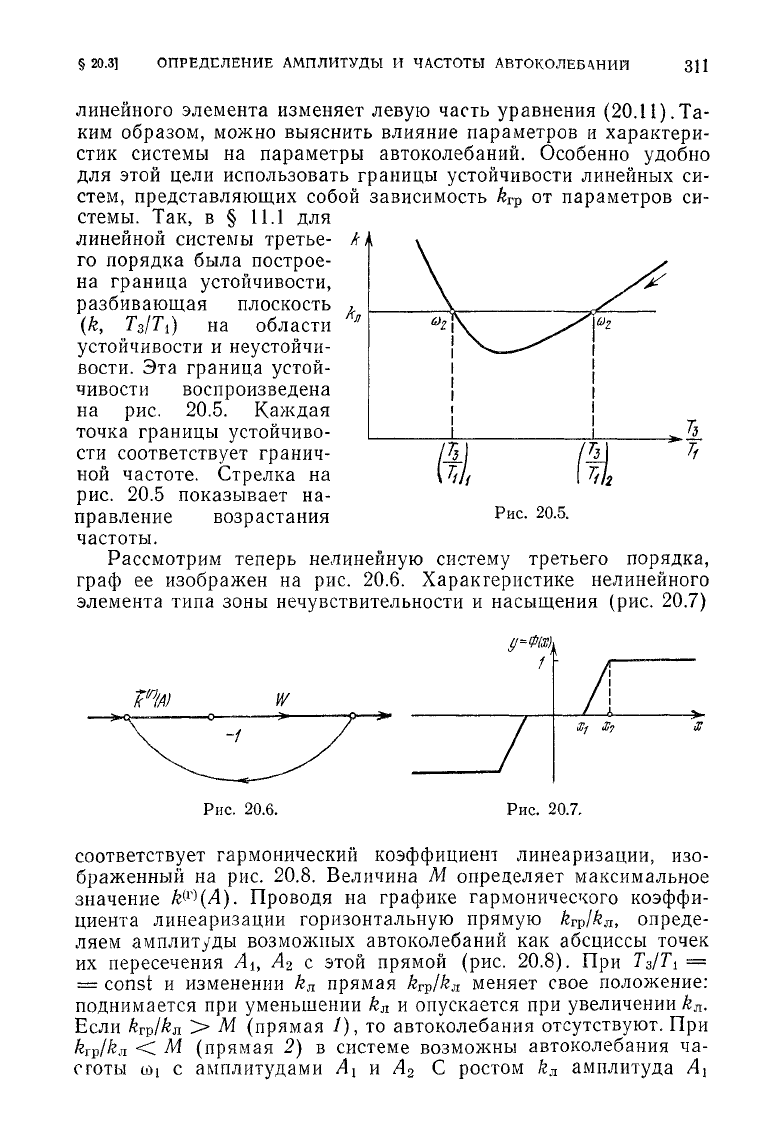
стемы. Так, в §
11.1
для
линейной
системы третье-
го порядка была построе-
на
граница устойчивости,
разбивающая плоскость
(/г,
Тз/Ti)
на области
устойчивости и неустойчи-
вости. Эта граница устой-
чивости воспроизведена
на
рис. 20.5. Каждая
точка границы устойчиво-
сти соответствует гранич-
ной
частоте. Стрелка на
рис.
20.5 показывает на-
правление возрастания
частоты.
Рассмотрим теперь нелинейную систему третьего порядка,
граф ее изображен на рис. 20.6. Характеристике нелинейного
элемента типа зоны нечувствительности и насыщения (рис. 20.7)
Рис.
20.5.
у-
7
А
3J?
Рис.
20.6.
Рис.
20.7,
соответствует гармонический коэффициент линеаризации, изо-
браженный на рис. 20.8. Величина М определяет максимальное
значение
k^(A).
Проводя на графике гармонического
коэффи-
циента
линеаризации горизонтальную прямую
&
гр
/й
л
,
опреде-
ляем амплитуды возможных автоколебаний как абсциссы точек
их пересечения
А
и
А
2
с этой прямой (рис. 20.8). При
Т
3
/Т
{
=
=
const и изменении
k
R
прямая
&
Г
р/&л
меняет свое положение:
поднимается при уменьшении
k
R
и
опускается при увеличении
й
л
.
Если
ferp/^л
>*
М
(прямая
/),
то автоколебания
отсутствуют.
При
&гр/&л
<
М
(прямая 2) в системе возможны автоколебания ча-
стоты
o)i
с амплитудами
А
г
и
А
2
С ростом
k
R
амплитуда
А
х
