Цыпкин Я.З Основы теории автоматических систем
Подождите немного. Документ загружается.


382
ПРОЦЕССЫ
В
ИМПУЛЬСНЫХ СИСТЕМАХ
[ГЛ.
26
Задачи
26.1.
Показать,
что
коэффициенты ошибок импульсной системы
на рис.
26.1
равны
в(О)
-о
L.
и
что
с(0)
и
с(1)
совпадают
с
коэффициентами ошибок предельной непрерыв-
ной
системы.
f(mT)
x(wl)
F
(P)
ip
(PJ
JL
ki
(Г?р+/)(Г
2
р+ф
z(mT)
Zip)
Рис.
26.1.
26.2. Показать,
что в
импульсной системе, рассмотренной
в
задаче
25.3,
установившееся значение ошибки
при
линейном воздействии
равно
f
(пгТ)
=
aTm
а
26.3. Найги вынужденный процесс
z
b
(t)
в
импульсной системе
на рис.
26.1
по
коэффициентам ошибок
с(0),
с(\),
с(2)
при
полиномиальном воздействии
26.4.
Чем
отличаются вынужденные процессы
при
гармоническом воздей-
ствии
в
импульсных
и
непрерывных
системах?

Глава
2?
УСТОЙЧИВОСТЬ
ИМПУЛЬСНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ
§
27Л.
Условия устойчивости
Будем говорить,
что
импульсная автоматическая система
устойчива
тогда
и
только
тогда,
когда
ее
реакция
на
любое огра-
ниченное
внешнее воздействие
ограничена.
Если
же
реакция
им-
пульсной системы хотя
бы на
одно ограниченное внешнее
воз-
действие
не
ограничена,
то
такая система
неустойчива.
Воспользуемся этим определением устойчивости
для
установ-
ления
условий устойчивости.
Для
этой цели рассмотрим уравне-
ние
импульсной системы
k
{sT)
f
((m
-
s)
Г).
(27.1)
2
Предположим,
что
внешнее воздействие
при
любом значении
ар-
гумента ограничено:
|
f
(mT)
|<
М
для
всех
пг
>
0.
(27.2)
Тогда, оценивая
по
абсолютной величине
левую
часть
(27.1)
и
учитывая,
что
абсолютная величина суммы
не
превосходит
сум-
му абсолютных величин, получим
m
\z(mT)\^Z\k(sT)\\f((m-s)T)\,
или,
принимая
во
внимание
(27.2),
|г(тГ)|<Л1
£|ft(s7H
(27.3)
0
Увеличивая верхний предел суммы
в
(27.3)
до
оо, мы
лишь
уси*
лим
неравенство. Таким образом,
оо
12
(m/)|<
M
£
|/г
(sr)|,
m
=
0,1,2,...
(27.4)
5
=
J

384
УСТОЙЧИВОСТЬ
ИМПУЛЬСНЫХ
АВТОМАТИЧЕСКИХ
СИСТЕМ
ГГЛ
2?
Импульсная
система
будет
устойчива, если
ряд,
стоящий
в
пра-
вой
части неравенства (27.4), сходится,
т. е.
если
оо
Yu\k{sT)\<oo.
(27.5)
Таким
образом,
I
импульсная
система
устойчива,
если
ряд
дискрет
времен-
ной характеристики
абсолютно
сходится.
Предположим теперь,
что
условие (27.5)
не
выполнено,
т. е.
S-0
(27.6)
Тогда найдется такое ограниченное воздействие (27.2),
при
кото-
ром
z(mT)
будет
не
ограничено. Действительно, зафиксируем
пг
и
выберем
f
{{m-s)T)
=
M
sign
k{sT).
Тогда
из
(27.6) получим
m
m
z
(mT)
—
Mj^k
(sT)
sign
k
{sT)
=
M
£
| k
(sT)
|.
Поскольку
такой выбор можно осуществить
при
любом наперед
заданном
m,
TO
z(mT)
в
силу (27.6)
будет
неограниченно возра-
стать
с
ростом
т,
что
свидетельствует
о
неустойчивости импульс-
ной
системы. Таким образом,
абсолютная
сходимость
дискрет
временной
характеристи-
ки (27.5) является
необходимым
и
достаточным
условием
устойчивости
импульсной
системы.
Как
было показано
в §
26.1,
процесс
в
линейной импульсной
системе, вызываемый внешним воздействием, можно представить
в
виде суммы вынужденного
z*(mT)
и
свободного процессов
z
c
(mT):
z{mT)^
z
B
(mT)
+
z
c
{mT),
где
z
c
(mT)^-
£
k(sT)f({m-s)T).
При
ограниченном внешнем воздействии (27.2) имеем
<М
Z
\k(sT)\.

§
27.1]
УСЛОВИЯ
УСТОЙЧИВОСТИ
385
Но
если ряд дискрет временной характеристики абсолютно схо-
оо
дится (27.5),
то
его остаток
2
|
k(sT)
|
при
т
—>
оо стремится
s~m+\
к
нулю. Это значит,
что в
устойчивой импульсной системе
с ро-
стом времени
т
свободный процесс
г
с
(тТ)
стремится
к
нулю,
а следовательно, общий процесс
z(mT) с
ростом времени
тТ
стремится
к
вынужденному процессу
г
ъ
(пгТ).
Таким образом,
1
в
устойчивых
импульсных
системах
с
течением
времени
устанавливается
вынужденный
процесс
z
B
(mT).
По
определению дискретного преобразования Лапласа
if
(р)
=
D { k
(sT) }
=
Е
ft
(sT)
е-Р*т,
откуда
следует
\КГ{р)\<1*\Ш)\\е-Р*т\.
(27.7)
Если
Rep^O,
то
|e~^
sr
|^l
и,
значит,
из
(27.7) получаем
Для
Из
этого неравенства
и
абсолютной сходимости ряда
дискрег
временной
характеристики (27.5)
следует,
что
передаточная
функция
К*(р)
устойчивой импульсной системы должна быть
ограничена
в
правой полуполосе
Rep
^
0, т. е.
К*(р) не должно
иметь особых
точек
—
полюсов
в
правой полуполосе
Rep^Q.
Таким
образом,
импульсная
система
будет
устойчива
только
тогда,
когда
все
полюсы
К*(р)
будут
расположены
в
левой
полу
по-
лосе,
или,
короче,
если
все
полосы
К*(р)
—
левые.
Но,
как
следует
из
(25.18), полюсы
/С*(р)
определяются
ну-
лями
характеристического многочлена
G*(p).
Поэтому
мы
при-
ходим
к
заключению, что
I
импульсная
система
будет
устойчива,
если
все
нули
ха-
рактеристического
многочлена
G*(p)
будут
левые.
Непосредственное вычисление нулей характеристического
многочлена
G*(p)
представляет собой весьма громоздкую опе-
рацию,
которая
при
степени многочлена выше
4
может быть
основана
лишь
на
численных методах. Поэтому важно найти
критерии
устойчивости, которые позволяют установить факт
устойчивости нулей характеристического многочлена.
13
Я, 3.
Цыпкин
386
УСТОЙЧИВОСТЬ
ИМПУЛЬСНЫХ
АВТОМАТИЧЕСКИХ
СИСТЕМ
[ГЛ. 27
Мы
рассмотрим здесь две формы критериев устойчивости —
алгебраическую, связанную с рассмотрением характеристиче-
ского многочлена
G*(p),
и частотную, связанную с
рассмотре-
нием
частотной характеристики разомкнутой импульсной си-
стемы
И7*(/со).
§
27.2. Алгебраический критерий устойчивости
Запишем
характеристический многочлен в раскрытой форме:
G*{p)
=
a
Q
eP
nT
+
a
l
e^
n
~
l)T
+
... +
а
п
.
(27.8)
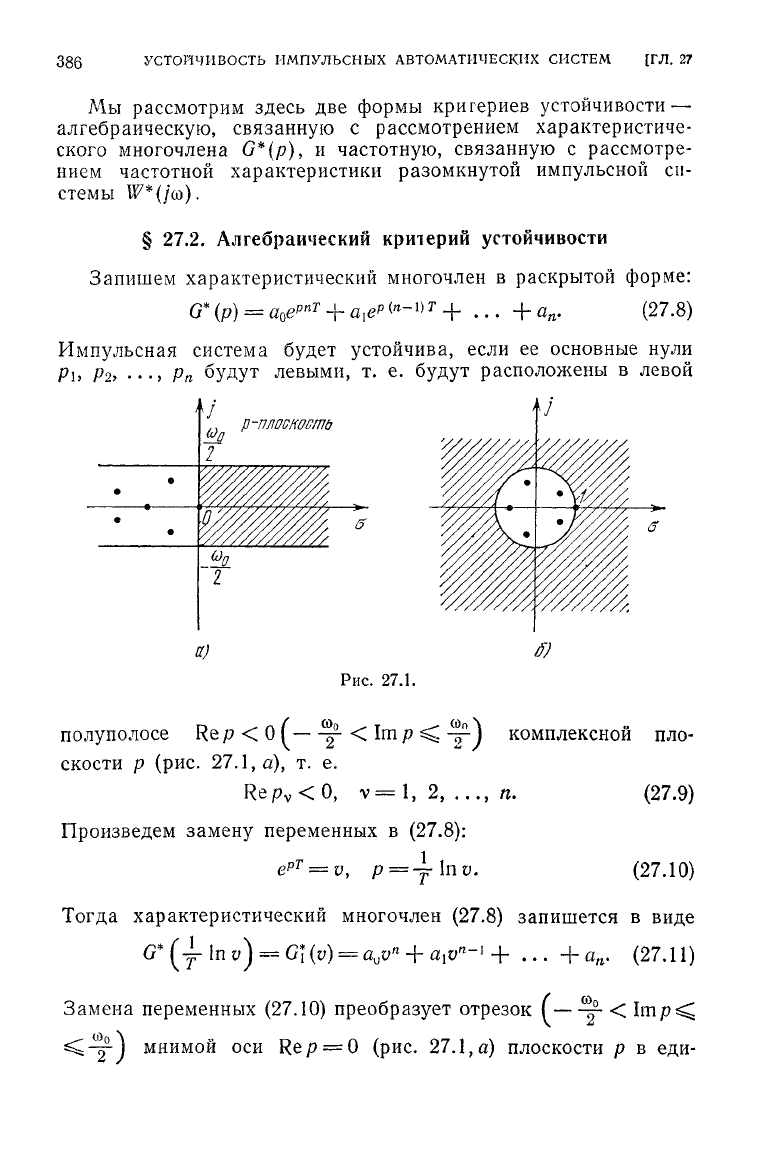
Импульсная
система
будет
устойчива, если ее основные нули
Ри
р2>
•••> Рп
будут
левыми, т. е.
будут
расположены в левой
tig
1
р-ллоскооть
0)
0
Рис.
27.1.
полуполосе Re р <
О
Г
— -—• <
Im
p ^ ^
скости р (рис. 27.1, а), т. е.
Rep
v
<0,
v==l,
2, ..., п.
комплексной
пло-
(27.9)
Произведем замену переменных в (27.8):
pT
p
ln
Y
v
'
(27.10)
Тогда характеристический многочлен
(27.8)
запишется в виде
l
-
1
+
... +
а
п
.
(27.11)
Замена
переменных
(27.10)
преобразует отрезок
(—
~- <
^-^-J
мнимой оси
Rep
= 0 (рис.
27.1,а)
плоскости р в
еди-

§
27.2] АЛГЕБРАИЧЕСКИЙ
КРИТЕРИЙ
УСТОЙЧИВОСТИ 387
ничную окружность
v
=
e^
T
на плоскости (рис.
27.1,6).
Левая
полуполоса Rep
<
0
(—
-^ <
Imp
<
•—-)
(рис. 27.1, а) пло-
скости р преобразуется во внутренность круга v —
e
pT
(Rep<0)
плоскости v (рис.
27.1,6),
а правая полуполоса
Rep>0
(—
-у-
< Imp ^
-—-J
плоскости р (рис. 27.1, а)
—во
внешнюю
часть круга v
=
e
pT
{Rep>0)
плоскости v (рис.
27.1,6).
И
значит, импульсная система
будет
устойчива, если все нули
характеристического многочлена
G*i(v)
(27.11)
будут
располо-
жены внутри единичной окружности, или если все нули
Vi
=
e
PlT
,
...,
v
n
=
e
PnT
будут
внутренними, т. е.
\v
v
\<\,
v=l, 2, ..., п.
(27.12)
Наиболее простой путь получения алгебраического критерия
устойчивости импульсных систем состоит в сведении этой задачи
к
уже известной нам формулировке алгебраического критерия
Рауса
— Гурвица (§
11.2).
Для этой цели произведем еще одну
замену переменной. Положим в
(27.11)
Тогда после умножения (27.11) на (и—
1)"
получим
=
a
o
("+l)"
+
ai(«+l)"~
I
("-l)+
...
+а
я
(и-1)
я
,
или,
после раскрытия скобок и приведения подобных
членов,
G
2
(и) =
А
й
и
п
+
Л,ы«-1
+ ...
+А
п
,
(27.13)
где
П
—»-2
я—1.
(27.14)
)
=
i
(k
_
ч|
— биномиальные
коэффициенты.
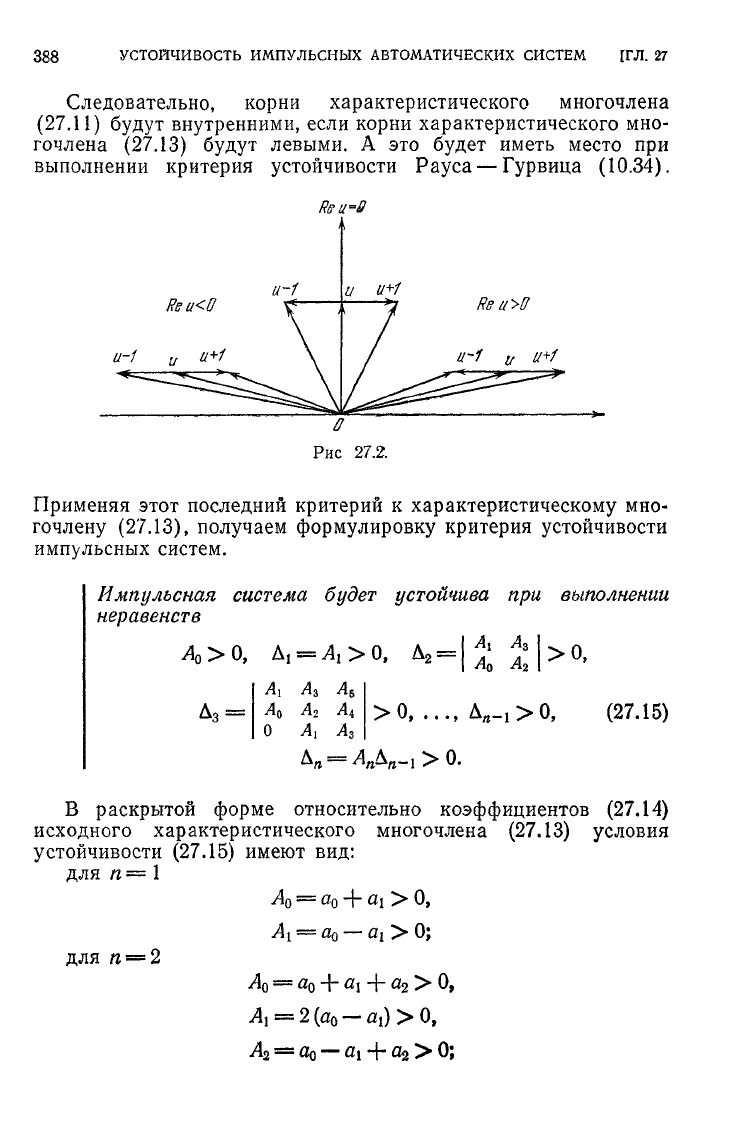
Как видно
непосредственно из рис. 27.2,
если Re и > 0, то | v \ >
1;
если
Re&
< 0, то | v | < 1;
если
Rew
= 0, то
\v\=l.
13*
388
УСТОЙЧИВОСТЬ ИМПУЛЬСНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ [ГЛ. 27
Следовательно, корни характеристического многочлена
(27.11)
будут
внутренними, если корни характеристического мно-
гочлена
(27.13)
будут
левыми. А это
будет
иметь место при
выполнении
критерия устойчивости
Рауса
—
Гурвица (10.34).
Rd
u>0
Применяя
этот последний критерий к характеристическому мно-
гочлену (27.13), получаем формулировку критерия устойчивости
импульсных систем.
Импульсная
система
будет
устойчива
при
выполнении
неравенств
Л
0
>0,
А
1
=
А,=
А\
Л
3
А
5
л
0
л
2
л
4
О
А
х
А
3
,
А
2
=
>0, ...,
Д^
(27.15)
В раскрытой форме относительно коэффициентов (27.14)
исходного характеристического многочлена (27.13) условия
устойчивости
(27.15)
имеют вид:
для
п = 1
Л
=
а
0
+
а
х
> 0,
=
#о
—
^i
> 0;
для
/г
==
2
Л
о
==
а
0
а
2
> 0,
А
==
а
0
—
а
х
+
02
> 0;

§
27.3]
ЧАСТОТНЫЙ
КРИТЕРИЙ
УСТОЙЧИВОСТИ
389
для
лг
==
3
Ао
=
а
о
+
а
{
+
а
2
+
а
3
>
О,
Л
1
=
3
(a
Q
—
а
3
)
+
а
{
—
а
2
> О,
Л
2
= 3
(OQ
+
а
3
)
—
ai
—
а
2
>
О,
Л
=
#0
—
«1
+
а>2
— % >
О»
А
Л
~ АЛ
==
а
0
—
а
\ +
а
1
п
Ъ
—
%
п
2
>
0
и т. д.
При
исследовании устойчивости конкретных импульсных си-
стем, когда коэффициенты заданы в числовой форме, можно
также воспользоваться таблицей Рауса, которая была приве-
дена в § 10.2.
§
27.3.
Частотный
критерий
устойчивости
Для установления частотного критерия устойчивости рассмо-
трим знаменатель
Т*(р)
передаточной функции замкнутой им-
пульсной системы
К*(р):
Г(р)=1
+
Г*(р),
(27.16)
где
W
*
{P)
=
1?W)
(27Л7)
— передаточная функция разомкнутой системы. Подставляя
W*(p) из (27.17) в (27.16), получим
Числитель этой функции представляет характеристический мно-
гочлен замкнутой системы
G*(p),
а
знаменатель
— характерис-
тический
многочлен разомкнутой импульсной системы
W*(p).
Частотный критерий устойчивости может быть получен на ос-
нове сопоставления устойчивости замкнутой и разомкнутой
импульсных систем.
Что касается разомкнутой системы, характеризуемой пере-
даточной функцией
W*(p),
то, как видно из выражения (27.17),
основные
полюсы ее совпадают с полюсами передаточной функ-
ции
непрерывной части W(p). Поэтому разомкнутая импульсная
система
будет
устойчива, если устойчива ее непрерывная часть.
В этом
случае
все полюсы
W(p),
а значит,
W*(p)
будут
левыми.
Замкнутая импульсная система
будет
устойчива, если все
нули Т*(р)
будут
левыми,
Производя замену переменной
(27.10), запишем Т*(р) в виде
=
r
i
(v)
=
^
r
.
(27.19)

390
УСТОЙЧИВОСТЬ ИМПУЛЬСНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ [ГЛ. 27
Замкнутая импульсная система
будет
устойчивой, если все нули
функции
T*(v)
будут
принадлежать единичному
кругу,
т.е. бу-
дут внутренними. Рассмотрим на комплексной плоскости v кон-
тур, представляющий собой окружность единичного радиуса с
центром в начале координат (рис.
27.1,6).
Предположим, что на
этом контуре нет ни нулей, ни полюсов функции
T*(v)
(27.19).
Представим
T\{v)
в виде
П
(»-«*)
П(—
О
l
где
i^
— нули,
v%
— полюсы
Г*
(и).
При изменении v вдоль еди-
ничной
окружности \v\= 1 по часовой стрелке каждый множи-
тель
(и
—
v*}
изменяет свой аргумент на
—2я,
если нуль
v*
ле-
жит внутри единичной окружности, и не меняет своего аргумен-
та, если нуль
v*
лежит вне единичной окружности (рис. 27.3, а),
J
Рис.
27.3.
а каждый множитель
(и
—
i>!J)
изменяет свой аргумент на
2я,
если полюс
v™
лежит внутри единичной окружности, и не меняет
своего аргумента, если полюс
с"
лежит вне единичной окруж-
ности
(рис.
27.3,6).
Отсюда
следует,
что при изменении v вдоль
контура единичной окружности
|и|=
1 по часовой стрелке из-
менение
аргумента
T*(v)
будет
равно 2я, помноженному на
раз-
ность
между
числом полюсов
N
n
и числом нулей
iV
H
,
лежащих
внутри контура, т. е.
(27.20)

i
27.3]
ЧАСТОТНЫЙ
КРИТЕРИЙ
УСТОЙЧИВОСТИ
391
Предположим вначале, что разомкнутая система устойчива. Это
значит, что все полюсы
Т*
(v) лежат внутри единичного круга,
т. е.
Но,
как было сказано выше, замкнутая система
будет
устойчива,
если все нули
Т*(р)
будут
лежать внутри единичного круга, т.е.
если
Таким
образом, замкнутая система
будет
устойчива, если
(27.21)
т. е. если при изменении v вдоль окружности единичного радиу-
са \v\= 1 изменение аргумента
T*(v)
будет
равно нулю.
Изображая
на плоскости
Т*
кривую
T*(v)
при
|и|=1
или,
что то же самое, кривую
Г*
(/со) Г—
-у-
<
со
<
уЛ
(рис. 27.4),
заключаем, что изменение аргумента
будет
равно нулю, если
начало координат (0, /0)
будет
находиться вне кривой
Т*
(/со).
W(JQ)
Рис.
27.4.
Функция
Г*(/со),
полученная из
(27.16)
при р = /со, связана
непосредственно с частотной характеристикой разомкнутой си-
стемы:
Представим частотную характеристику
в
виде
(27.22)
где
k
—
коэффициент усиления, a
IF*
(/со)
—
нормированная час-
тотная характеристика разомкнутой системы. Составим функцию
Очевидно, что
(27.23)
