Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

392

УСТОЙЧИВОСТЬ

ИМПУЛЬСНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ [ГЛ. 27

Начало координат (0, /0) в плоскости Т* или плоскости

Т1

(рис.27.4, а) соответствует точке

(—1,

/0) в плоскости

или

точке

(*~"X'^J

в плоскости

(27.4,6).

Поэтому условие

устойчивости (27.21)

будет

выполнено, если точка

—

-т-,

/0J

не

будет

охватываться нормированной частотной характеристикой

W*(j®)(

—

^к-

<co^-y-J.

В силу симметрии частотной характе-

ристики

относительно действительной оси при

со

—-у-можно

изображать на графике лишь частотную

характеристику для неотрицательных частот. Таким образом, мы

приходим к следующей формулировке частотного критерия устой-

чивости.

Частотный

критерий I

(точечный

критерий).

Импульсная

система

устойчивой

непрерывной

частью

будет

устойчива

тогда

только

тогда,

когда

нормированная

частотная

ха-

рактеристика

W*(jd))

разомкнутой

импульсной

системы

не

охватывает

точку

(

—

-g,

Если

нас интересует устойчивость замкнутой импульсной

си-

стемы при значениях коэффициента усиления

принадлежащих

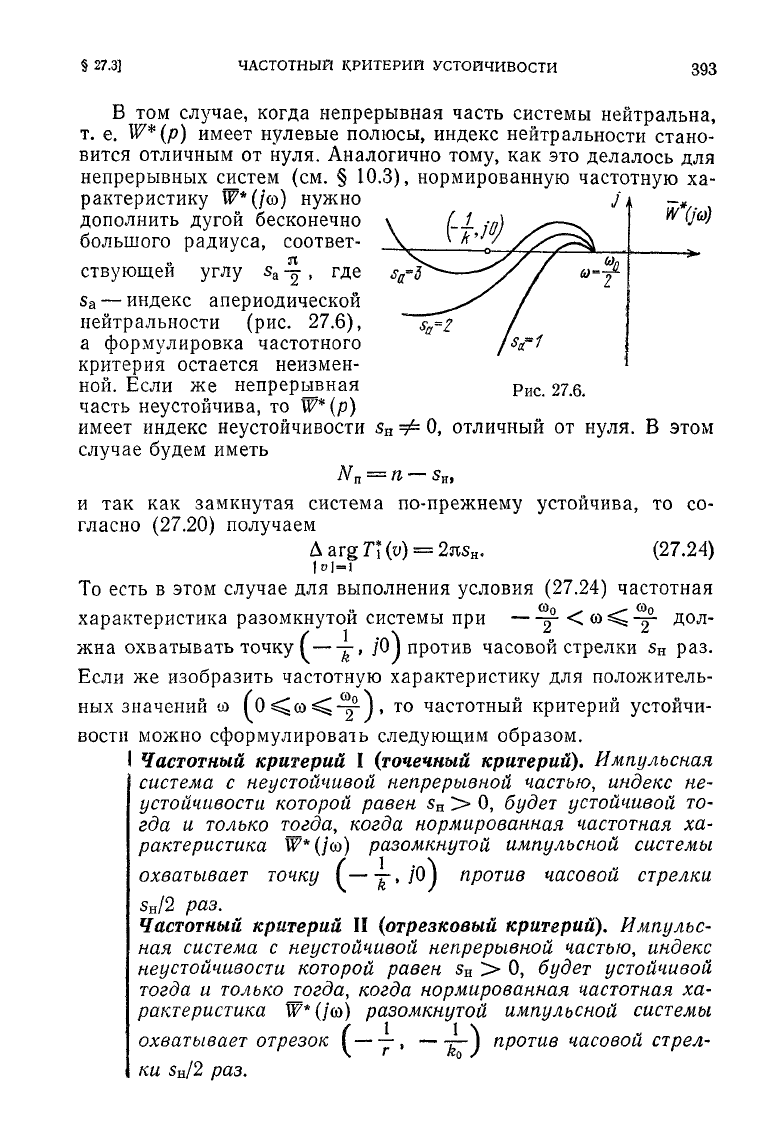
Рис.

27.5.

интервалу

(г,

т.е.

<С

&o,

то в этом случае частотный

критерий

устойчивости можно сформулировать в следующей

форме.

Частотный

критерий

(отрезковый

критерий). Импульс-

ная

система

устойчивой

непрерывной

частью

будет

устойчивой

при

тогда

только

тогда,

когда

нормированная

частотная

характеристика

W*(/co)

разо-

мкнутой

импульсной

системы

не

охватывает

и не

пересе-

/1 1 \

кает

отрезок

—т~Ь

Примеры,

иллюстрирующие применения критериев устойчи-

вости, изображены на рис. 27.5, а, б.

27.3]

ЧАСТОТНЫЙ

КРИТЕРИЙ

УСТОЙЧИВОСТИ

393

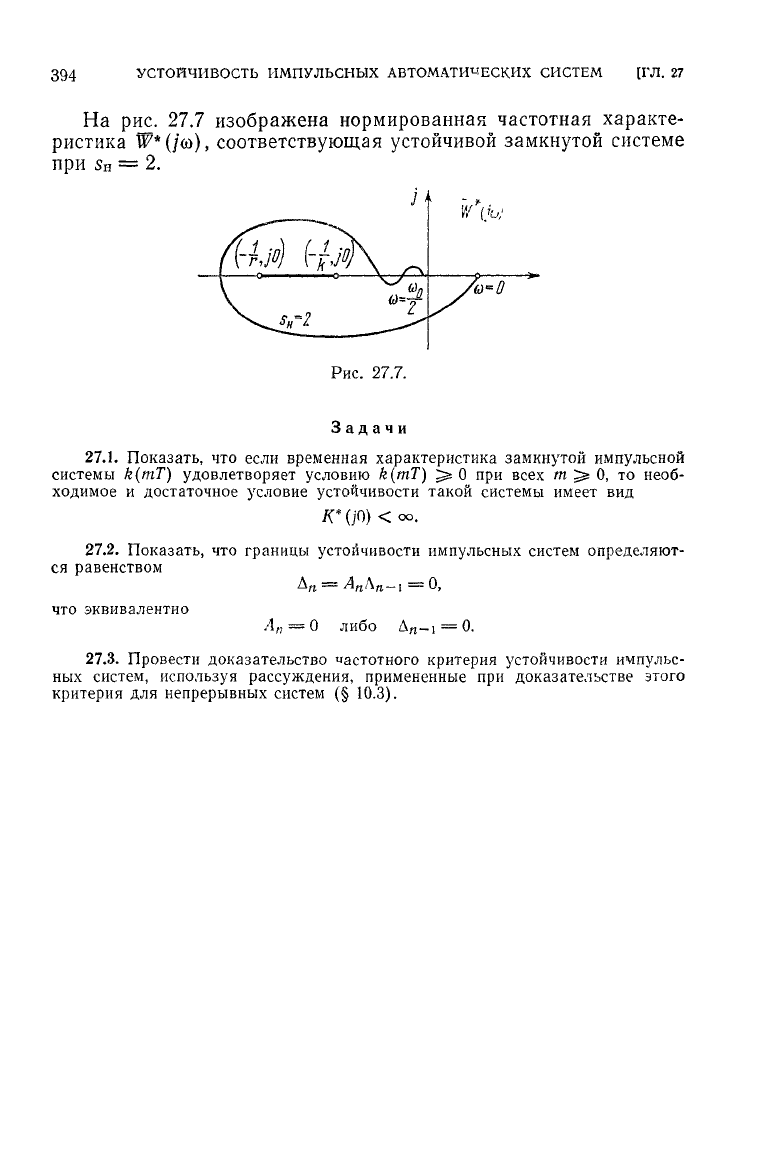
В том случае, когда непрерывная часть системы нейтральна,

т. е.

W*(p)

имеет нулевые полюсы, индекс нейтральности стано-

вится отличным от нуля. Аналогично тому, как это делалось для

непрерывных систем (см. § 10.3), нормированную частотную

ха~

W*(]Q)

рактеристику

W*(/co)

нужно

дополнить дугой бесконечно

большого радиуса, соответ-

ствующей

углу

-g-,

где

— индекс апериодической

нейтральности (рис. 27.6),

а формулировка частотного

критерия

остается неизмен-

ной.

Если же непрерывная

часть неустойчива, то

W*(p)

имеет индекс неустойчивости

Ф 0, отличный от нуля. В этом

случае будем иметь

так как замкнутая система по-прежнему устойчива, то со-

гласно (27.20) получаем

(27.24)

Рис.

27.6.

То есть в этом случае для выполнения условия (27.24) частотная

характеристика разомкнутой системы при —

-у-

< со ^

-у-

дол-

жна охватывать точку

(

—

у,

/0J

против часовой стрелки

раз.

Если

же изобразить частотную характеристику для положитель-

ных значений со

Го^со<1-у1,

то частотный критерий устойчи-

вости можно сформулировать следующим образом.

Частотный

критерий I

(точечный

критерий).

Импульсная

система

неустойчивой

непрерывной

частью,

индекс

не-

устойчивости

которой

равен

будет

устойчивой

то-

гда и

только

тогда,

когда

нормированная

частотная

ха-

рактеристика

(/со)

разомкнутой

импульсной

системы

охватывает

точку

(—

-г-,

/0J

против

часовой

стрелки

раз.

Частотный

критерий II

(отрезковый

критерий).

Импульс-

ная

система

неустойчивой

непрерывной

частью,

индекс

неустойчивости

которой

равен

> 0,

будет

устойчивой

тогда

только

тогда,

когда

нормированная

частотная

ха-

рактеристика

(/со)

разомкнутой

импульсной

системы

охватывает

отрезок

(

—-т-J

против

часовой

стрел-

ки

раз.

394

УСТОЙЧИВОСТЬ

ИМПУЛЬСНЫХ

АВТОМАТИЧЕСКИХ

СИСТЕМ

{ГЛ. 27

На

рис. 27.7 изображена нормированная частотная характе-

ристика

IF*

(/со), соответствующая устойчивой замкнутой системе

при

= 2.

Рис.

27.7.

Задачи

27.1.

Показать, что если временная характеристика замкнутой импульсной

системы

k(mT)

удовлетворяет условию

k(mT)

при

всех

0, то необ-

ходимое и достаточное условие устойчивости такой системы имеет вид

К'

(/0) <

оо.

27.2. Показать, что границы устойчивости импульсных систем определяют-

ся

равенством

ЛЛ

что эквивалентно

либо

-i=0.

27.3.

Провести доказательство частотного критерия устойчивости импульс-

ных систем, используя рассуждения, примененные при доказательстве этого

критерия

для непрерывных систем (§ 10.3).

Глава

ИССЛЕДОВАНИЕ

УСТОЙЧИВОСТИ

ИМПУЛЬСНЫХ

СИСТЕМ

28.1. Исследование устойчивости

типовых

импульсных

систем

Рассмотрим

вначале общую форму характеристических мно-

гочленов импульсных систем первого и второго порядка. Для

многочлена

первой степени

G*(/7)

согласно условиям устойчивости (§ 27.2) имеем

£i>O,

—

>0,

(28.1)

или

при

> О

Область устойчивости изображена на рис. 28.1. Она соответ-

ствует отрезку

(—1,1)

на прямой

ai/a

0 1

Рис.

28.1.

Для многочлена второй степени G*(p) =

{

еР

из

тех же условий устойчивости имеем

> О,

> 0, (28.2)

#о

{

> О

или

при

> 0

396

ИССЛЕДОВАНИЕ

УСТОЙЧИВОСТИ

ИМПУЛЬСНЫХ

СИСТЕМ

[ГЛ.

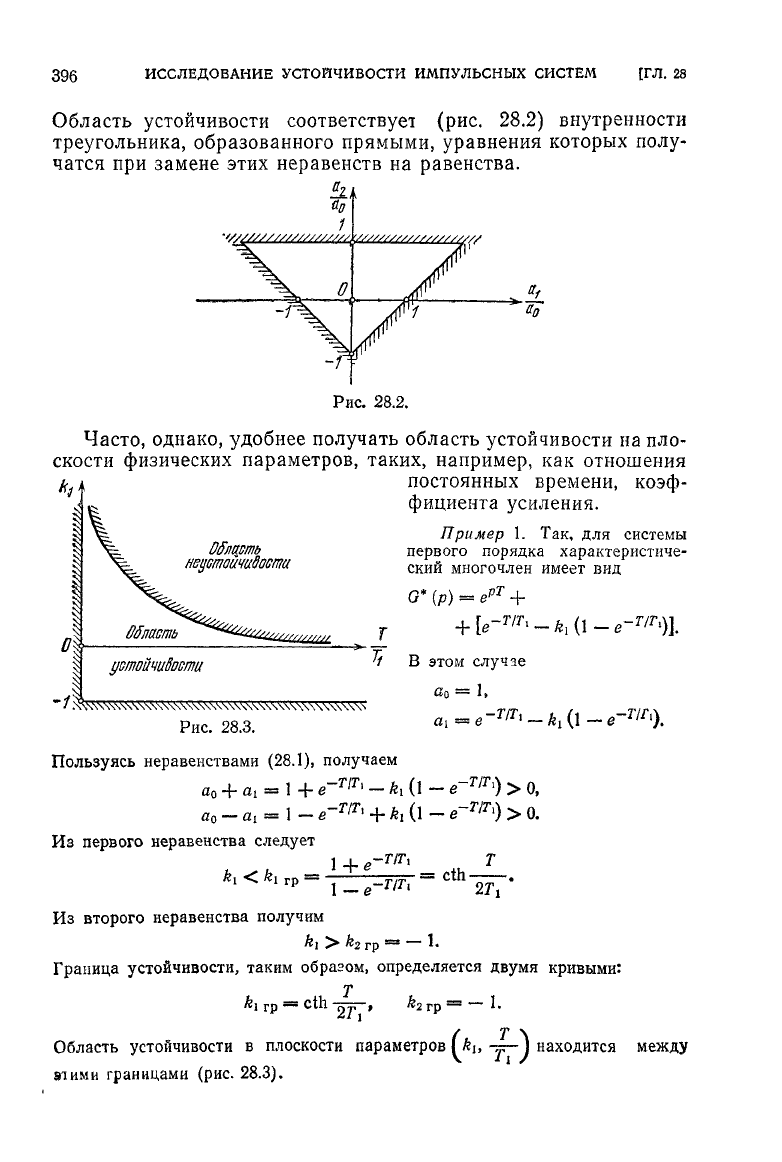
Область устойчивости соответствует

(рис. 28.2)

внутренности

треугольника, образованного прямыми, уравнения которых полу-

чатся

при

замене этих неравенств

на

равенства.

Часто,

однако, удобнее получать область устойчивости

на

пло-

скости физических параметров, таких, например,

как

отношения

постоянных

времени,

коэф-

фициента

усиления.

Область

нвустойчидооти

Пример

1. Так, для

системы

первого порядка характеристиче-

ский

многочлен имеет

вид

(р) =

рТ

Оёлпсть

уатюйчибооти

"*'

.N^\\\^\\\\\NN\NN\\\\\\V\\\^

Рис.

28.3.

этом случае

••е

— ;

•е-Щ.

Пользуясь неравенствами (28.1), получаем

а,

' -

А,

Г/Г

О,

но

- а, - 1 -

TIT

+ fti (1 -

е-

г/г

> 0.

Из

первого неравенства

следует

cth-

Из

второго неравенства получим

Граница устойчивости, таким образом, определяется двумя кривыми:

cth

~2f->

—

Область устойчивости

плоскости параметров

-j~J

находится между

алими

границами (рис. 28.3),

}

28.1]

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ТИПОВЫХ СИСТЕМ

397

Пример

2. Для импульсной системы второго порядка с простейшим им-

пульсным элементом характеристический многочлен второго порядка имеет

вид

В этом

случае

ПО

= 1,

= 1 + е~

' '

— k\

—

П2

e~~

Пользуясь неравенствами (28.2), получаем

#о

~t~

—

(1 +

е~

—-

(1 —

)

—

1 —

е~

г/Г1

> 0,

«о

—

П\

—

е~

Тх

)

> 0.

Из

первого неравенства получаем

T/Tl

го

—-I-——--

= 2

cth

Второе и третье неравенства выполняются при

всех

положительных парамет-

рах, т. е. граница устойчивости

определяется двумя кривыми:

Область

неустойчивости

Область

уотойчибости

'Tf

Рис.

28.4.

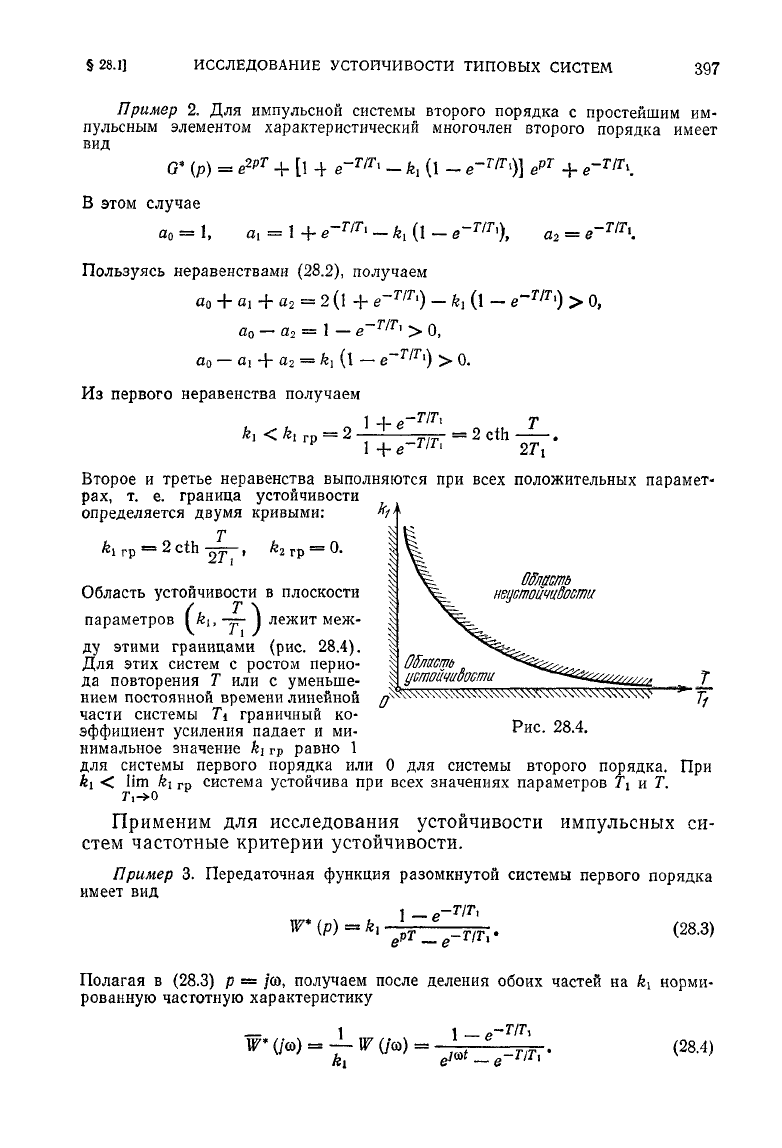
Область устойчивости в плоскости

параметров

—

лежит меж-

ду этими границами (рис. 28.4).

Для этих систем с ростом перио-

да повторения Т или с уменьше-

нием

постоянной времени линейной

части системы

Т\

граничный ко-

эффициент

усиления падает и ми-

нимальное значение

гр

равно 1

для системы первого порядка или 0 для системы второго порядка. При

k\ <

lim

система устойчива при

всех

значениях параметров

Т\

и Т.

Применим

для исследования устойчивости импульсных си-

стем частотные критерии устойчивости.

Пример

3. Передаточная функция разомкнутой системы первого порядка

имеет вид

(28.3)

Полагая

(28.3)

р = /со, получаем после деления обоих частей на

норми-

рованную частотную характеристику

(/©)

(/СО)

~TIT

(28.4)

398

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ

[ГЛ.

Эта

нормированная частотная характеристика изображена на рис. 28.5. Как

следует из (28.4),

(JO)

=7=г

= —

TITl

2Г,

Замкнутая

импульсная система будет устойчива, если точка

("Т-")

W (jo)

Рис.

28.5.

не

будет охватываться нормирован-

ной

частотной характеристикой, т. е.

если

~~TT

"2fT

Отсюда получаем

cth

2j-

что совпадает с ранее полученным ус-

ловием.

отличие

от

непрерывных

систем

первого

второго

по-

рядка

(см. §

11.1),

устойчивых

при

любых

положительных

значениях

коэффициента

усиления,

импульсные

системы

первого

второго

порядка

всегда

имеют

предельный

ко-

эффициент

усиления,

превышение

которого

приводит

к не-

устойчивости.

28.2. Устойчивость

импульсных

систем

при малых периодах повторения

Рассмотрим типовую импульсную систему с произвольной не-

прерывной

частью и импульсным элементом, формирующим пря-

моугольные импульсы

(рис.

28.6). Частотная характеристика

приведенной

непрерывной части

равна

f(mT)

^js(mT)

(jO)

Рис.

28.6.

а частотная характеристика разомкнутой импульсной системы

представится в виде

оо

или,

более подробно,

-/(со-гсо

)Г

ГЩ

)Т

HM/>-rco

)).

28.3]

ВЛИЯНИЕ

ЧАСТОТЫ

ПОВТОРЕНИЯ

399

Так

как

со

= — , т. е.

со

2я,

то

(У

(со

Щ)

. (28.5)

При

достаточно малом периоде повторения Г, что

соответствует

достаточно

оолыпои

частоте повторения

==-у-,

можно в пра-

вой

части

(28.5)

ограничиться наибольшим слагаемым, соответ-

ствующим

О,

тогда

приближенно

будем

иметь

или,

поскольку при

соГ

<С

;ЪГ

1Ш

п—е

W(JQ)

i(t)

Z(P)

/соГ

^__

ТО

W*(h)

«e"

°"l)F

(/a)).

(28,6)

Из

(28.6)

следует,

что при достаточно малых периодах повто-

рения

импульсную систему можно рассматривать как непрерыв-

ную систему, содержащую ту же

непрерывную часть и элемент

f(t)^

запаздывания (рис. 28.7). Эта

непрерывная

система образует-

ся

из импульсной заменой им-

пульсного элемента, формирую-

Рис

28.7.

щего прямоугольные импульсы,

элементом запаздывания, осуществляющего запаздывание на

время,

равное половине периода повторения

. Но, как было

показано

в §

11.5,

наличие запаздывания

всегда

приводит к су-

ществованию конечного граничного коэффициента усиления.

Этот факт объясняет, почему, в отличие от непрерывных

систем,

импульсные системы первого и второго порядка

всегда

имеют

конечный

граничный коэффициент усиления.

28.3.

Влияние

частоты

повторения

на

устойчивость

импульсных

систем

Как

уже отмечалось, частотная характеристика разомкнутой

импульсной системы связана с частотной характеристикой при-

веденной непрерывной части соотношением

(28.7)

400

ИССЛЕДОВАНИЕ

УСТОЙЧИВОСТИ

ИМПУЛЬСНЫХ

СИСТЕМ

1ГЛ. 28

Для построения

W*(jco)

W (/со) можно поступить следующим

образом. Зададимся частотой повторения

и на приведенной

частотной характеристике непрерывной части

(J<U)

S(J®)W

(JQ)

(рис.

28.8) отметим точку

-у-.

Затем выберем в интервале ча-

стот

0<со<-у-

значение

И отметим на частотной ха-

рактеристике W (/со)

точки

со

—- со

со

2со

—

со

2со

т. д. Замечая, что

значения

(гсо

— со)) и

(©!

—

гсо

))

комплексно со-

пряженные,

из точки

со!

на ча-

стотной характеристике строим

ломаную линию из векторов,

соответствующих W (/

(со

))

О)

Рис.

28,8.

ристики

(20

ot>i))

и т. д. Так как

с ростом

модуль частотной

характеристики W (/

(г©

со^)

стремится к нулю, то практи-

чески ломаная векторов

будет

содержать конечное число

векторов (рис. 28.8), и конеч-

ная

точка ломаной и есть точ-

ка

со

соответствующая

значению частотной характе-

масштабе -^- при

Для частоты

(28.7)

получаем

Г=1

Отсюда

следует,

что точка

IF*

(/-^г)

частотной характеристики

разомкнутой импульсной системы всегда лежит на вещественной

оси

и равна сумме вещественных частей частотной характери-

стики

приведенной непрерывной части при соответствующих ча-

стотах

(в

масштабе

~Н

(рис. 28.8).

Для достаточно высокой частоты повторения в

(28.7)

можно

ограничиться двумя слагаемыми, соответствующими г = 0 и

ВЛИЯНИЕ

ЧАСТОТЫ

ПОВТОРЕНИЯ

40!

1. Тогда

(/®)

"§•

(/®)

(/ (

^o))].

(28.8)

В этом случае вместо ломаной, указывающей переход от

W(j®)

W*(j®)

мы

будем

иметь лишь один вектор

Щ/(соо—

со)). Со-

отношение

(28.8) особенно удобно для качественного исследова-

ния

влияния частоты повторения

на

устойчивость импульсной си-

стемы.

Предположим, что частотная ха-

рактеристика приведенной непре-

рывной

системы расположена в

нижней

полуплоскости (рис. 28.9).

Такими

частотными характеристи-

ками

обладают системы не выше

второго порядка, а также системы

более высокого порядка, но устойчи-

вые при любом положительном ко-

эффициенте

усиления. В этом слу-

чае применение способа построе-

ния

W*(j(o)

W(jto)

приводит к тому, что частотная характе-

ристика

W*(/со) расположена слева от

W(/co)

и при

со

зна-

Рис.

28.9.

чение

частотной

характеристики

ТТГ7*

( •

О)0

[]

~о~)

отлично от нуля и

отрицательно, что свидетельствует о наличии конечного гранич-

ного коэффициента усиления

"(/*)•

а это имеет место при любом соо

оо.

Таким образом,

если

W(j(u)

расположена

нижней

полуплоскости,

то вве-

дение

простейшего

импульсного

элемента

непрерывную

систему

приводит

возникновению

конечного

граничного

коэффициента

усиления.

Частота

на

границе

устойчивости

при

этом

наивысшая

равна

-^-.

Предположим, что частотная характеристика приведенной не-

прерывной

части расположена в левой полуплоскости (рис.

28.10),

Такими

частотными характеристиками обладают системы треть-

его порядка, а также системы более высокого порядка, если мо-

дуль

высокочастотной части частотной характеристики весьма

мал и этой частью мы можем пренебречь. В этом случае, строя

W*(jco)

W(j®),

заключаем, что в низкочастотной области

вплоть до

со

гр

частотная характеристика

W*(j<o)

расположе-