Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.

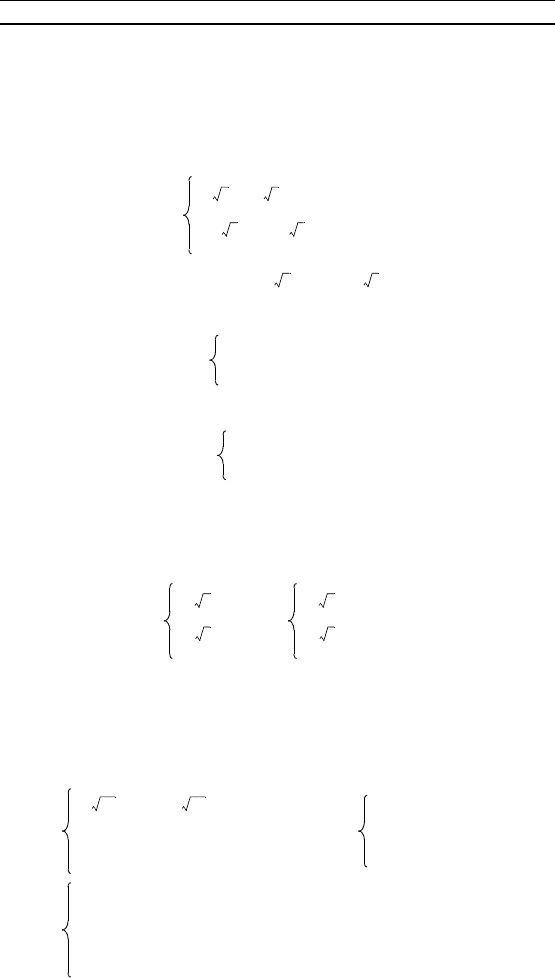
80 Г л а в а 3. Системы уравнений
Неоторые системы лоарифмичесих или поазательных
уравнений сводятся системам рациональных уравнений непо-
средственной заменой входящих в них лоарифмов (или соот-
ветственно степеней) новыми неизвестными.
П р и м е р 3. Решить систему уравнений
Р е ш е н и е. Полаая z = и u = , приходим систе-
ме рациональных уравнений
оторая с учетом условий z > 0 и u > 0 эвивалентна системе
Решениями этой системы являются следующие пары чисел:
(25; 8); (8; 25).
Возвращаясь исходным неизвестным, получаем две систе-
мы уравнений
имеющие решения x = 8, y = 9 и x = (log
5
8)
3
, y = (log
2
25)
2
.
Ответ. (8; 9); (27 2; 4 5).
Решите систему уравнений:
20. 21.
22.
· = 200,
+ = 689.
5
x
3
2
y
5
2 x
3
2
2 y
5
x
3
2
y
zu = 200,
z
2
+ u
2
= 689,
zu = 200,
z + u = 33.
= 25,
= 8,
5
x
3
2
y
= 8,
= 25,
5
x
3
2
y
log
5
3
log
2
2
+ = 5,
+ = 8.
2
xy 2–
4
xy 1–
3 xy+()
xy–
----------------------
5 xy–()
xy+
----------------------
(x
2
+ y) · = 1,
9(x
2
+ y) = .
2
yx
2
–
6
x
2
y–
– 2 · = 71,
+ 2 · = 21,
+ = 16.
11
xz
5
y
11
z
5
y/2
11
(xz)z–
5
y/2
§ 16. Разные задачи 81
§ 16. Разные задачи
Решите систему уравнений:
1.
2.
3.
4.
5.
6.
7. z
x
= x, z
y
= y, y
y
= x.
8.
= x
2,5
,
log
3
y · log
y
(y – 2x) = 1.
yx
log
y
x
log
2
x + log
4
y + log
4
z = 2,
log
3
y + log
9
z + log
9
x = 2,
log
4
z + log
16
x + log
16
y = 2.
= 100 ,
= .
10
lg
1
2
---
x
2
y
2
+()1,5+
10
x
2
10y+
3
----------------------------
6
2 x
2
10y+9–
------------------------------------------
= y
2
,
= .
x
x
4
y+
y
2
3
y
x
4
y+
x
2
3
log
y
|log
y
x| = log
x
|log
x
y|,
lg
2
x + lg
2
y = 8.
log
12
x + log
2
y = log
2
x,
log
2
x · log
3
(x + y) = 3 log
3
x.
1
log
x
2
----------------
log
a
x · log
a
(xyz) = 48,
log
a
y · log
a
(xyz) = 12,
log
a
z · log
a
(xyz) = 84, a > 0, a − 1.
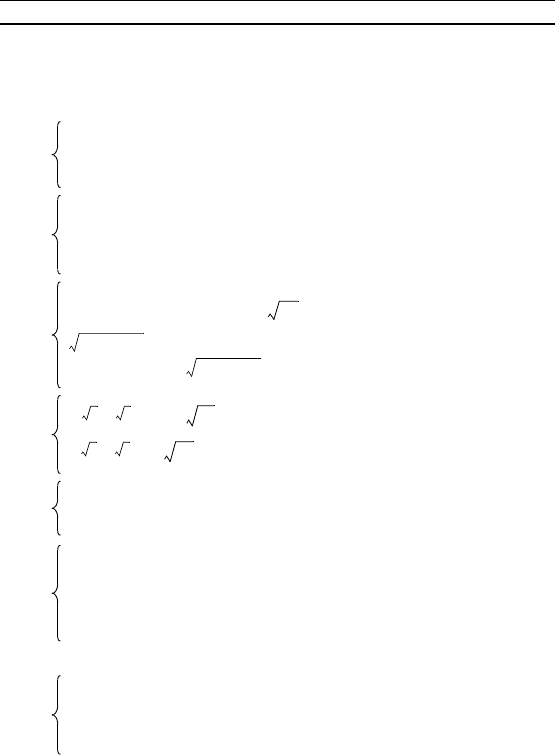
80 Г л а в а 3. Системы уравнений
Неоторые системы лоарифмичесих или поазательных
уравнений сводятся системам рациональных уравнений непо-
средственной заменой входящих в них лоарифмов (или соот-
ветственно степеней) новыми неизвестными.
П р и м е р 3. Решить систему уравнений
Р е ш е н и е. Полаая z = и u = , приходим систе-
ме рациональных уравнений
оторая с учетом условий z > 0 и u > 0 эвивалентна системе
Решениями этой системы являются следующие пары чисел:
(25; 8); (8; 25).
Возвращаясь исходным неизвестным, получаем две систе-
мы уравнений
имеющие решения x = 8, y = 9 и x = (log
5
8)
3
, y = (log
2
25)
2
.
Ответ. (8; 9); (27 2; 4 5).
Решите систему уравнений:
20. 21.
22.
· = 200,
+ = 689.
5
x
3
2
y
5
2 x
3
2
2 y
5
x
3
2
y
zu = 200,
z
2
+ u
2
= 689,
zu = 200,
z + u = 33.
= 25,
= 8,
5
x
3
2
y
= 8,
= 25,
5
x
3
2
y
log
5
3
log
2
2
+ = 5,
+ = 8.
2
xy 2–
4
xy 1–
3 xy+()
xy–
----------------------
5 xy–()
xy+
----------------------
(x
2
+ y) · = 1,
9(x
2
+ y) = .
2
yx
2
–
6
x
2
y–
– 2 · = 71,
+ 2 · = 21,
+ = 16.
11
xz
5
y
11
z
5
y/2
11
(xz)z–
5
y/2
§ 16. Разные задачи 81
§ 16. Разные задачи
Решите систему уравнений:
1.
2.
3.
4.
5.
6.
7. z
x
= x, z
y
= y, y
y
= x.
8.
= x
2,5
,
log
3
y · log
y
(y – 2x) = 1.
yx
log
y
x
log
2
x + log
4
y + log
4
z = 2,
log
3
y + log
9
z + log
9
x = 2,
log
4
z + log
16
x + log
16
y = 2.
= 100 ,
= .
10
lg
1
2
---
x
2
y
2
+()1,5+
10
x
2
10y+
3
----------------------------
6
2 x
2
10y+9–
------------------------------------------
= y
2
,
= .
x
x
4
y+
y
2
3
y
x
4
y+
x
2
3
log
y
|log
y
x| = log
x
|log
x
y|,
lg
2
x + lg
2
y = 8.
log
12
x + log
2
y = log
2
x,
log
2
x · log
3
(x + y) = 3 log
3
x.
1
log
x
2
----------------
log
a
x · log
a
(xyz) = 48,
log
a
y · log
a
(xyz) = 12,
log
a
z · log
a
(xyz) = 84, a > 0, a − 1.
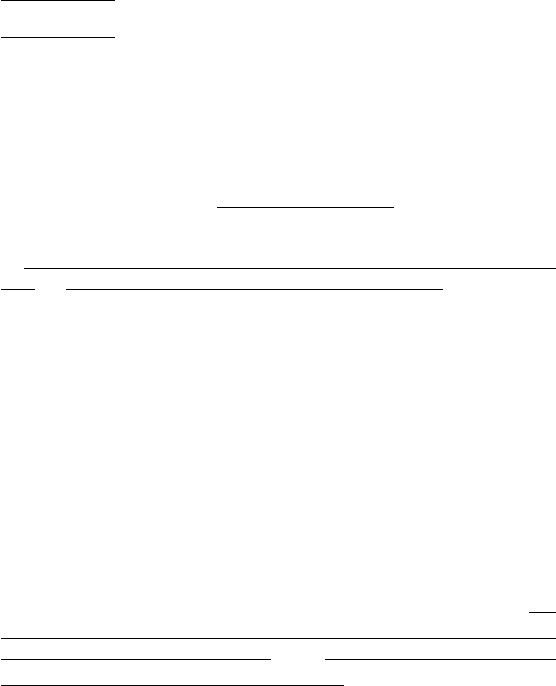
Глава 4
Неравенства.
Уравнения и неравенства
с параметрами
Пусть f(x) — числовая фунция одноо или несольих пе-
ременных (арументов). Решить неравенство
f(x) < 0 (f(x) > 0) (1)
— это значит найти все значения арумента (арументов) фун-
ции f, при оторых неравенство (1) справедливо. Множество
всех значений арумента (арументов) фунции f, при оторых
неравенство (1) справедливо, называют множеством решений
неравенства или просто решением неравенства.
Множество решений нестрооо неравенства
f(x) m 0 (f(x) l 0) (2)
представляет собой объединение множества решений неравен-
ства (1) и множества решений уравнения f(x) = 0.
Два неравенства называют эвивалентными, если множе-
ства их решений совпадают.
Под множеством допстимых значений неизвестных,
входящих в неравенство, понимают область определения фун-
ции f(x).
Неравенства вида (1) или (2), составленные для различных
фунций f
i
(x), моут быть сведены в систему неравенств. Ре-
шить систему неравенств — это значит найти множество всех
значений арументов фунций f
i
(x), при оторых справедливы
все неравенства системы одновременно.
Говорят, что системы неравенств эвивалентны, если мно-
жества их решений совпадают.
§ 17. Рациональные и иррациональные
неравенства
Алебраичесие неравенства. Линейными неравенствами
(строими и нестроими) называют неравенства вида
ax + b > 0, ax + b < 0, ax + b l 0, ax + b m 0, a − 0,
решениями оторых являются соответственно следующие про-
межути:
§ 17. Рациональные и иррациональные неравенства 83
если a > 0, то
x Ý – ; +× , x Ý –×; – , x Ý – ; +× , x Ý –×; – ;
если a < 0, то
x Ý –×; – , x Ý – ; +× , x Ý –×; – , x Ý – ; +× .
Квадратными неравенствами (строими и нестроими)
называют неравенства вида
ax
2
+ bx + c > 0, ax
2
+ bx + c < 0,
ax
2
+ bx + c l 0, ax
2
+ bx + c m 0,
де a, b, c— неоторые действительные числа и a − 0.
Квадратное неравенство ax
2
+ bx + c > 0 в зависимости
от значений своих оэффициентов a, b, c имеет следующие ре-
шения:
если a > 0 и D = b
2
– 4ac l 0, то
x Ý –×; Ÿ ; +× ;
если a > 0 и D < 0, то x Ý R (т. е. x— любое действительное
число);
если a < 0 и D > 0, то
x Ý ; ;
если a < 0 и D < 0, то x Ý ¾ (т. е. решений нет).
Решение неравенства ax
2
+ bx + c < 0 сводится решению
рассмотренноо неравенства, если обе части исходноо неравен-
ства умножить на (–1).
Метод интервалов. Пусть P
n
(x)— мноочлен n-й степени
с действительными оэффициентами, а c
1
, c
2
, ..., c
i
— все дейст-
вительные орни мноочлена, ратности оторых соответствен-
но равны k
1
, k
2
, ..., k
i
, причем c
1
> c
2
> ... > c
i
. Мноочлен P
n
(x)
можно представить в виде
P
n
(x) = x – c
1
x – c
2
... x – c
i
Q
m
(x), (3)
де мноочлен Q
m
(x) не имеет действительных орней и либо
положителен, либо отрицателен при всех x Ý R. Положим для
b
a
---
b
a
---
b
a
---
b
a
---
b
a
---
b
a
---
b
a
---
b
a
---
b– D–
2a
-----------------------
b– D+
2a
----------------------- -
b– D–
2a
-----------------------
b– D+
2a
----------------------- -
()
k
1
()
k
2
()
k
l

Глава 4
Неравенства.
Уравнения и неравенства
с параметрами
Пусть f(x) — числовая фунция одноо или несольих пе-
ременных (арументов). Решить неравенство
f(x) < 0 (f(x) > 0) (1)
— это значит найти все значения арумента (арументов) фун-
ции f, при оторых неравенство (1) справедливо. Множество
всех значений арумента (арументов) фунции f, при оторых
неравенство (1) справедливо, называют множеством решений
неравенства или просто решением неравенства.
Множество решений нестрооо неравенства
f(x) m 0 (f(x) l 0) (2)
представляет собой объединение множества решений неравен-
ства (1) и множества решений уравнения f(x) = 0.
Два неравенства называют эвивалентными, если множе-
ства их решений совпадают.
Под множеством допстимых значений неизвестных,
входящих в неравенство, понимают область определения фун-
ции f(x).
Неравенства вида (1) или (2), составленные для различных
фунций f
i
(x), моут быть сведены в систему неравенств. Ре-
шить систему неравенств — это значит найти множество всех
значений арументов фунций f
i
(x), при оторых справедливы
все неравенства системы одновременно.
Говорят, что системы неравенств эвивалентны, если мно-
жества их решений совпадают.
§ 17. Рациональные и иррациональные
неравенства
Алебраичесие неравенства. Линейными неравенствами
(строими и нестроими) называют неравенства вида
ax + b > 0, ax + b < 0, ax + b l 0, ax + b m 0, a − 0,
решениями оторых являются соответственно следующие про-
межути:
§ 17. Рациональные и иррациональные неравенства 83
если a > 0, то
x Ý – ; +× , x Ý –×; – , x Ý – ; +× , x Ý –×; – ;
если a < 0, то
x Ý –×; – , x Ý – ; +× , x Ý –×; – , x Ý – ; +× .
Квадратными неравенствами (строими и нестроими)
называют неравенства вида
ax
2
+ bx + c > 0, ax
2
+ bx + c < 0,
ax
2
+ bx + c l 0, ax
2
+ bx + c m 0,
де a, b, c— неоторые действительные числа и a − 0.
Квадратное неравенство ax
2
+ bx + c > 0 в зависимости
от значений своих оэффициентов a, b, c имеет следующие ре-
шения:
если a > 0 и D = b
2
– 4ac l 0, то
x Ý –×; Ÿ ; +× ;
если a > 0 и D < 0, то x Ý R (т. е. x— любое действительное
число);
если a < 0 и D > 0, то
x Ý ; ;
если a < 0 и D < 0, то x Ý ¾ (т. е. решений нет).
Решение неравенства ax
2
+ bx + c < 0 сводится решению
рассмотренноо неравенства, если обе части исходноо неравен-
ства умножить на (–1).
Метод интервалов. Пусть P
n
(x)— мноочлен n-й степени
с действительными оэффициентами, а c
1
, c
2
, ..., c
i
— все дейст-
вительные орни мноочлена, ратности оторых соответствен-
но равны k
1
, k
2
, ..., k
i
, причем c
1
> c
2
> ... > c
i
. Мноочлен P
n
(x)
можно представить в виде
P
n
(x) = x – c
1
x – c
2
... x – c
i
Q
m
(x), (3)
де мноочлен Q
m
(x) не имеет действительных орней и либо
положителен, либо отрицателен при всех x Ý R. Положим для
b
a
---
b
a
---
b
a
---
b
a
---
b
a
---
b
a
---
b
a
---
b
a
---
b– D–
2a
-----------------------
b– D+
2a
----------------------- -
b– D–
2a
-----------------------
b– D+
2a
----------------------- -
()
k
1
()
k
2
()
k
l

84 Г л а в а 4. Неравенства. Уравнения и неравенства с параметрами
определенности, что Q
m
(x) > 0. Тода при x > c
i
все сомножите-
ли в разложении (3) положительны и P
n
(x) > 0. Если c
1
— о-
рень нечетной ратности (k
1
— нечетное), то при x Ý (c
2
; c
1
) все
сомножители в разложении (3), за ислючением первоо, поло-
жительны и, значит, P
n
(x) < 0 при x Ý (c
2
; c
1
). В этом случае
оворят, что мноочлен P
n
(x) меняет зна при переходе через
орень c
1
. Если же c
1
— орень четной ратности (k
1
— чет-
ное), то все сомножители (в том числе и первый) при x Ý (c
2
; c
1
)
положительны и, следовательно, P
n
(x) > 0 при x Ý (c
2
; c
1
).
В этом случае оворят, что мноочлен P
n
(x) не меняет знаа
при переходе через орень c
1
.
Аналоично, используя разложение (3), нетрудно убедить-
ся, что при переходе через орень c
2
мноочлен P
n
(x) меняет
зна, если k
2
— нечетное, и не меняет знаа, если k
2
— четное.
Рассмотренное свойство мноочленов используется для реше-
ния неравенств методом интервалов. Для тоо чтобы найти
все решения неравенства
P
n
(x) > 0, (4)
достаточно знать все действительные орни мноочлена P
n
(x),
их ратности и зна мноочлена P
n
(x) в произвольно выбран-
ной точе, не совпадающей с орнем мноочлена.
П р и м е р 1. Решить неравенство
x
4
+ 3x
3
– 4x > 0. (*)
Р е ш е н и е. Разложим на множители мноочлен P
4
(x), на-
ходящийся в левой части неравенства (*). Вынося множитель x
за соби, получаем
P
4
(x) = x(x
3
+ 3x
2
– 4).
Второй сомножитель, представляющий собой убичесий мно-
очлен, имеет орень x = 1. Следовательно, уазанный мноо-
член можно представить та:
x
3
+ 3x
2
– 4 = (x – 1) (x
2
+ 4x + 4) = (x – 1) (x + 2)
2
.
Поэтому P
4
(x) = x(x – 1) (x + 2)
2
и неравенство (*) можно пред-
ставить в виде
x(x – 1) (x + 2)
2
> 0. (**)
Решим неравенство (**) методом интервалов. При x > 1 все
сомножители, записанные в левой части неравенства, положи-
тельны.
§ 17. Рациональные и иррациональные неравенства 85
Будем двиаться по оси Ox справа налево. При переходе
через точу x = 1 мноочлен P
4
(x) меняет зна и принимает от-
рицательные значения, та а x = 1— простой орень (о-
рень ратности 1); при переходе через точу x = 0 мноочлен
таже меняет зна и принимает положительные значения, по-
сольу x = 0 — таже простой орень; при переходе через точ-
у x = –2 мноочлен не меняет знаа, та а x = –2 — орень
ратности 2. Промежути знаопосто-
янства мноочлена P
4
(x) схематичеси
изображены на рис. 1. Используя этот
рисуно, лео записать множество ре-
шений исходноо неравенства.
Ответ. x Ý (–×; –2) Ÿ (–2; 0) Ÿ (1; +×).
Рациональные неравенства. Решение рациональноо нера-
венства, т. е. неравенства вида
> 0, (5)
де P
n
(x) и Q
m
(x) — мноочлены, сводится решению эвива-
лентноо неравенства (4) следующим образом: умножив обе
части неравенства (5) на мноочлен (Q
m
(x))
2
, оторый положи-
телен при всех допустимых значениях неизвестноо x (т. е. при
тех x, для оторых Q
m
(x) − 0), получим неравенство
P
n
(x) · Q
m
(x) > 0,
эвивалентное неравенству (5).
Дробно-линейными неравенствами называют неравенства
вида
> k, (6)
де a, b, c, d, k— неоторые действительные числа, причем c − 0
и − (если c = 0, то дробно-линейное неравенство превраща-
ется в линейное, а если = , то неравенство (6) не содержит
арумента). К дробно-линейным неравенствам относятся и не-
равенства вида (6), де вместо знаа > записаны знаи <, l, m.
Решение дробно-линейноо неравенства сводится решению
вадратноо неравенства. Для этоо необходимо умножить обе
части неравенства (6) на выражение (cx + d)
2
, положительное
при всех x Ý R и x − – .
+
–2 0 1
+
x
+
–
Рис. 1
P
n
x()
Q
m
x()
-----------------
ax b+
cx d+
-----------------
a
c
---
b
d
---
a
c
---
b
d
---
d
c
---

84 Г л а в а 4. Неравенства. Уравнения и неравенства с параметрами
определенности, что Q
m
(x) > 0. Тода при x > c
i
все сомножите-
ли в разложении (3) положительны и P
n
(x) > 0. Если c
1
— о-
рень нечетной ратности (k
1
— нечетное), то при x Ý (c
2
; c
1
) все
сомножители в разложении (3), за ислючением первоо, поло-
жительны и, значит, P
n
(x) < 0 при x Ý (c
2
; c
1
). В этом случае
оворят, что мноочлен P
n
(x) меняет зна при переходе через
орень c
1
. Если же c
1
— орень четной ратности (k
1
— чет-
ное), то все сомножители (в том числе и первый) при x Ý (c
2
; c
1
)
положительны и, следовательно, P
n
(x) > 0 при x Ý (c
2
; c
1
).
В этом случае оворят, что мноочлен P
n
(x) не меняет знаа
при переходе через орень c
1
.
Аналоично, используя разложение (3), нетрудно убедить-
ся, что при переходе через орень c
2
мноочлен P
n
(x) меняет
зна, если k
2
— нечетное, и не меняет знаа, если k
2
— четное.
Рассмотренное свойство мноочленов используется для реше-
ния неравенств методом интервалов. Для тоо чтобы найти
все решения неравенства
P
n
(x) > 0, (4)
достаточно знать все действительные орни мноочлена P
n
(x),
их ратности и зна мноочлена P
n
(x) в произвольно выбран-
ной точе, не совпадающей с орнем мноочлена.
П р и м е р 1. Решить неравенство
x
4
+ 3x
3
– 4x > 0. (*)
Р е ш е н и е. Разложим на множители мноочлен P
4
(x), на-
ходящийся в левой части неравенства (*). Вынося множитель x
за соби, получаем
P
4
(x) = x(x
3
+ 3x
2
– 4).
Второй сомножитель, представляющий собой убичесий мно-
очлен, имеет орень x = 1. Следовательно, уазанный мноо-
член можно представить та:
x
3
+ 3x
2
– 4 = (x – 1) (x
2
+ 4x + 4) = (x – 1) (x + 2)
2
.
Поэтому P
4
(x) = x(x – 1) (x + 2)
2
и неравенство (*) можно пред-
ставить в виде
x(x – 1) (x + 2)
2
> 0. (**)
Решим неравенство (**) методом интервалов. При x > 1 все
сомножители, записанные в левой части неравенства, положи-
тельны.
§ 17. Рациональные и иррациональные неравенства 85
Будем двиаться по оси Ox справа налево. При переходе
через точу x = 1 мноочлен P
4
(x) меняет зна и принимает от-
рицательные значения, та а x = 1— простой орень (о-
рень ратности 1); при переходе через точу x = 0 мноочлен
таже меняет зна и принимает положительные значения, по-
сольу x = 0 — таже простой орень; при переходе через точ-
у x = –2 мноочлен не меняет знаа, та а x = –2 — орень
ратности 2. Промежути знаопосто-
янства мноочлена P
4
(x) схематичеси
изображены на рис. 1. Используя этот
рисуно, лео записать множество ре-
шений исходноо неравенства.
Ответ. x Ý (–×; –2) Ÿ (–2; 0) Ÿ (1; +×).
Рациональные неравенства. Решение рациональноо нера-
венства, т. е. неравенства вида
> 0, (5)
де P
n
(x) и Q
m
(x) — мноочлены, сводится решению эвива-
лентноо неравенства (4) следующим образом: умножив обе
части неравенства (5) на мноочлен (Q
m
(x))
2
, оторый положи-
телен при всех допустимых значениях неизвестноо x (т. е. при
тех x, для оторых Q
m
(x) − 0), получим неравенство
P
n
(x) · Q
m
(x) > 0,
эвивалентное неравенству (5).
Дробно-линейными неравенствами называют неравенства
вида
> k, (6)
де a, b, c, d, k— неоторые действительные числа, причем c − 0
и − (если c = 0, то дробно-линейное неравенство превраща-
ется в линейное, а если = , то неравенство (6) не содержит
арумента). К дробно-линейным неравенствам относятся и не-
равенства вида (6), де вместо знаа > записаны знаи <, l, m.
Решение дробно-линейноо неравенства сводится решению
вадратноо неравенства. Для этоо необходимо умножить обе
части неравенства (6) на выражение (cx + d)
2
, положительное
при всех x Ý R и x − – .
+
–2 0 1
+
x
+
–
Рис. 1
P
n
x()
Q
m
x()
-----------------
ax b+
cx d+
-----------------
a
c
---
b
d
---
a
c
---
b
d
---
d
c
---

86 Г л а в а 4. Неравенства. Уравнения и неравенства с параметрами
П р и м е р 2. Решить неравенство
< –1.
Р е ш е н и е. Прибавив обеим частям неравенства по 1,
получаем неравенство вида (5):
< 0,
оторое эвивалентно неравенству
x
2
(x
2
– x – 2) < 0.
Множество решений последнео неравенства находим методом
интервалов: x Ý (–1; 0) Ÿ (0; 2).
Ответ. x Ý (–1; 0) Ÿ (0; 2).
Решите неравенство:
1. + < 1. 2. < .
3. (x + 1) (3 – x)(x – 2)
2
l 0. 4. l 1.
5. m 0. 6. < .
7. > 0. 8. m x.
9. < 0. 10. > –3.
Иррациональные неравенства. Под иррациональным не-
равенством понимается неравенство, в отором неизвестные
величины (или неоторые фунции неизвестных величин) на-
ходятся под знаом радиала. Для тоо чтобы найти множест-
во решений иррациональноо неравенства, приходится, а
правило, возводить обе части неравенства в натуральную сте-
пень. При этом (в силу принципиальной невозможности про-
вери полученных решений подстановой) необходимо следить
за тем, чтобы при преобразовании неравенств аждый раз по-
лучалось неравенство, эвивалентное исходному.
При решении иррациональных неравенств следует учиты-
вать, что возведение обеих частей неравенства в нечетную сте-
пень вседа приводит неравенству, эвивалентному исходно-
му. Если же обе части неравенства возвести в четную степень,
x 2+
x
2
x–2–
---------------------------
x
2
x
2
x–2–
---------------------------
1
2 x–
-------------
5
2 x+
------------- -
1
x 2+
------------- -
3
x 3–
-------------
x
2
3x–2+
x
2
3x 2++
-------------------------------
x
3
x
2
– x 1–+
x 8+
----------------------------------------
2x 5–
x
2
6x–7–
------------------------------
1
x 3–
-------------
x
3
2x
2
–5x–6+
x 2–
------------------------------------------------
2 x
2
–
1 x–
----------------
x 4–
4x
2
4x–3–
----------------------------------
x
2
2x–3+
x
2
4x–3+
-------------------------------
§ 17. Рациональные и иррациональные неравенства 87
то неравенство, эвивалентное исходному и имеющее тот же
зна, получится лишь в том случае, ода обе части исходноо
неравенства неотрицательны.
П р и м е р 3. Решить неравенство
< + . (*)
Р е ш е н и е. Множество допустимых значений неравенст-
ва (*) представляет собой промежуто [2; +×). На этом проме-
жуте обе части неравенства (*) неотрицательны; поэтому, воз-
ведя их в вадрат и приведя подобные члены, получим эвива-
лентное неравенство
6 – x < 2 . (**)
Рассмотрим теперь два возможных случая.
1. Если 6 – x < 0 (т. е. x > 6), то левая часть неравенства (**)
отрицательна, а правая — неотрицательна и, следовательно,
неравенство (**) справедливо при всех x Ý (6; +×).
2. Если 6 – x l 0, то при всех x Ý [2; 6] обе части неравенст-
ва (**) неотрицательны. Возведя их в вадрат, получаем нера-
венство
3x
2
– 28 > 0, (***)
решениями отороо с учетом сделанноо предположения о том,
что x Ý [2; 6], являются значения из промежута ; 6 .
Объединив множества решений, соответствующие двум рас-
смотренным случаям, оончательно получаем решение исход-
ноо неравенства — промежуто ; +× .
Ответ.; +× .
Решите неравенство:
11. – > 1. 12. – > 0.
13. – 2x + 3 > 0. 14. x + 4 < .
15. < . 16. < 1.
x 3+
x 1– x 2–
x
2
3x–2+
28
3
------
28
3
------
28
3
------
13x–
5 x+ 41x–– 2 x–
x
2
4x 5–+ x 46+
23x+– x 4+
24 2x– x
2
–
x
--------------------------------------
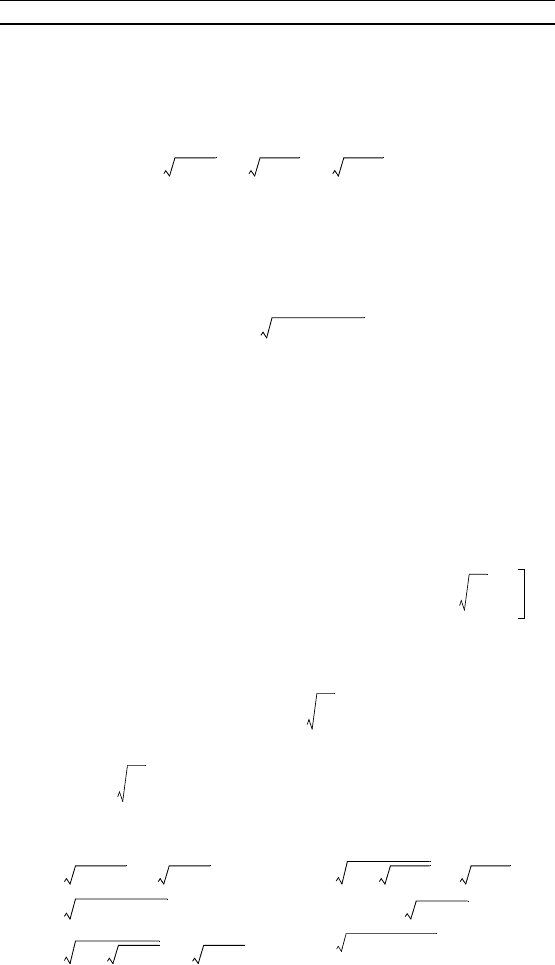
86 Г л а в а 4. Неравенства. Уравнения и неравенства с параметрами
П р и м е р 2. Решить неравенство
< –1.
Р е ш е н и е. Прибавив обеим частям неравенства по 1,
получаем неравенство вида (5):
< 0,
оторое эвивалентно неравенству
x
2
(x
2
– x – 2) < 0.
Множество решений последнео неравенства находим методом
интервалов: x Ý (–1; 0) Ÿ (0; 2).
Ответ. x Ý (–1; 0) Ÿ (0; 2).
Решите неравенство:
1. + < 1. 2. < .
3. (x + 1) (3 – x)(x – 2)
2
l 0. 4. l 1.
5. m 0. 6. < .
7. > 0. 8. m x.
9. < 0. 10. > –3.
Иррациональные неравенства. Под иррациональным не-
равенством понимается неравенство, в отором неизвестные
величины (или неоторые фунции неизвестных величин) на-
ходятся под знаом радиала. Для тоо чтобы найти множест-
во решений иррациональноо неравенства, приходится, а
правило, возводить обе части неравенства в натуральную сте-
пень. При этом (в силу принципиальной невозможности про-
вери полученных решений подстановой) необходимо следить
за тем, чтобы при преобразовании неравенств аждый раз по-
лучалось неравенство, эвивалентное исходному.
При решении иррациональных неравенств следует учиты-
вать, что возведение обеих частей неравенства в нечетную сте-
пень вседа приводит неравенству, эвивалентному исходно-
му. Если же обе части неравенства возвести в четную степень,
x 2+
x
2
x–2–
---------------------------
x
2
x
2
x–2–
---------------------------
1
2 x–
-------------
5
2 x+
------------- -
1
x 2+
------------- -
3
x 3–
-------------
x
2
3x–2+
x
2
3x 2++
-------------------------------
x
3
x
2
– x 1–+
x 8+
----------------------------------------
2x 5–
x
2
6x–7–
------------------------------
1
x 3–
-------------
x
3
2x
2
–5x–6+
x 2–
------------------------------------------------
2 x
2
–
1 x–
----------------
x 4–
4x
2
4x–3–
----------------------------------
x
2
2x–3+
x
2
4x–3+
-------------------------------
§ 17. Рациональные и иррациональные неравенства 87
то неравенство, эвивалентное исходному и имеющее тот же
зна, получится лишь в том случае, ода обе части исходноо
неравенства неотрицательны.
П р и м е р 3. Решить неравенство
< + . (*)
Р е ш е н и е. Множество допустимых значений неравенст-
ва (*) представляет собой промежуто [2; +×). На этом проме-
жуте обе части неравенства (*) неотрицательны; поэтому, воз-
ведя их в вадрат и приведя подобные члены, получим эвива-
лентное неравенство
6 – x < 2 . (**)
Рассмотрим теперь два возможных случая.
1. Если 6 – x < 0 (т. е. x > 6), то левая часть неравенства (**)
отрицательна, а правая — неотрицательна и, следовательно,
неравенство (**) справедливо при всех x Ý (6; +×).
2. Если 6 – x l 0, то при всех x Ý [2; 6] обе части неравенст-
ва (**) неотрицательны. Возведя их в вадрат, получаем нера-
венство
3x
2
– 28 > 0, (***)
решениями отороо с учетом сделанноо предположения о том,
что x Ý [2; 6], являются значения из промежута ; 6 .
Объединив множества решений, соответствующие двум рас-
смотренным случаям, оончательно получаем решение исход-
ноо неравенства — промежуто ; +× .
Ответ.; +× .
Решите неравенство:
11. – > 1. 12. – > 0.
13. – 2x + 3 > 0. 14. x + 4 < .
15. < . 16. < 1.
x 3+
x 1– x 2–
x
2
3x–2+
28
3
------
28
3
------
28
3
------
13x–
5 x+ 41x–– 2 x–
x
2
4x 5–+ x 46+
23x+– x 4+
24 2x– x
2
–
x
--------------------------------------
88 Г л а в а 4. Неравенства. Уравнения и неравенства с параметрами
17. < 1. 18. m 3.
19. – > x. 20. > .
21. l 2x + 3. 22. > –2.
23. + > .
24. – > 1.
Неравенства, содержащие неизвестное под знаом модля.
При решении неравенств, содержащих неизвестное под знаом
модуля, используют тот же способ, что и при решении анало-
ичных уравнений, а именно решение исходноо неравенства
сводят решению несольих неравенств, рассматриваемых на
промежутах знаопостоянства выражений, находящихся под
знаом модуля.
П р и м е р 4. Решить неравенство
|x
2
– 2| + x < 0. (*)
Р е ш е н и е. Рассмотрим промежути знаопостоянства вы-
ражения x
2
– 2, записанноо под знаом модуля.
1. Пусть x
2
– 2 l 0. Тода неравенство (*) примет вид
x
2
+ x – 2 < 0. (**)
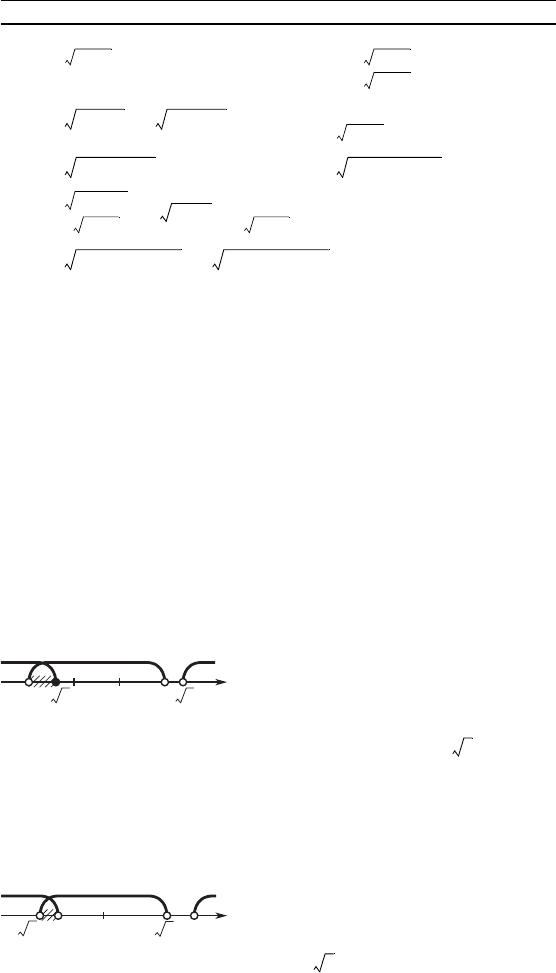
Пересечение множества решений
неравенства (**) и неравенства
x
2
– 2 l 0 представляет собой пер-
вое множество решений исходноо
неравенства: x Ý (–2; – ] (рис. 2).
2. Пусть x
2
– 2 < 0. Тода соласно определению модуля
имеем |x
2
– 2| = 2 – x
2
, и неравенство (*) примет вид
2 – x
2
+ x < 0. (***)
Пересечение множества решений
неравенства (***) и неравенства
x
2
– 2 < 0 дает второе множество
решений исходноо неравенства:
x Ý (– ; –1) (рис. 3).
x 5+
1 x–
------------------
4 x 1+–
1 x 3+–
----------------------------
8 x
2
– 25 x
2
–
1
1 x+
------------------
1
2 x–
-------------
x
2
x–2– x
2
3x 4++
x
2
16–
x 3–
----------------------- -
x 3–
5
x 3–
----------------- -
3x
2
5x 7++ 3x
2
5x 2++
–2 0 1
x
–
2
2
Рис. 2
2
–1
02
x
–
2
2
Рис. 3
2
§ 17. Рациональные и иррациональные неравенства 89
Объединяя найденные множества решений, оончательно
получаем x Ý (–2; –1).
Ответ. x Ý (–2; –1).
В отличие от уравнений неравенства не допусают непо-
средственной провери. Однао во мноих случаях можно убе-
диться в правильности полученных результатов рафичесим
способом. Действительно, запишем неравенство из примера 4
в виде
|x
2
– 2| < –x.
Построим рафии фунций y
1
= |x
2
– 2| и y
2
= –x, входящих
в левую и правую части рассматриваемоо неравенства, и най-
дем те значения арумента, при оторых y
1
< y
2
.
На рис. 4 заштрихованная часть оси абсцисс содержит исо-
мые значения x.
Решение неравенств, содержащих зна модуля, инода
можно значительно соратить, используя равенство |x
2
| = x
2
.
П р и м е р 5. Решить неравенство
> 1. (*)
Р е ш е н и е. Исходное неравенство при всех x − –2 эвива-
лентно неравенству
|x – 1| > |x + 2|. (**)
Возведя обе части неравенства (**) в вадрат, после приве-
дения подобных членов получаем неравенство
6x < –3,
т. е. x < – 0,5.
x
O
y
y
2
= –x
–2
2
–1
–
2
2
y
1
= |x
2
– 2|
Рис. 4
x 1–
x 2+
------------- -
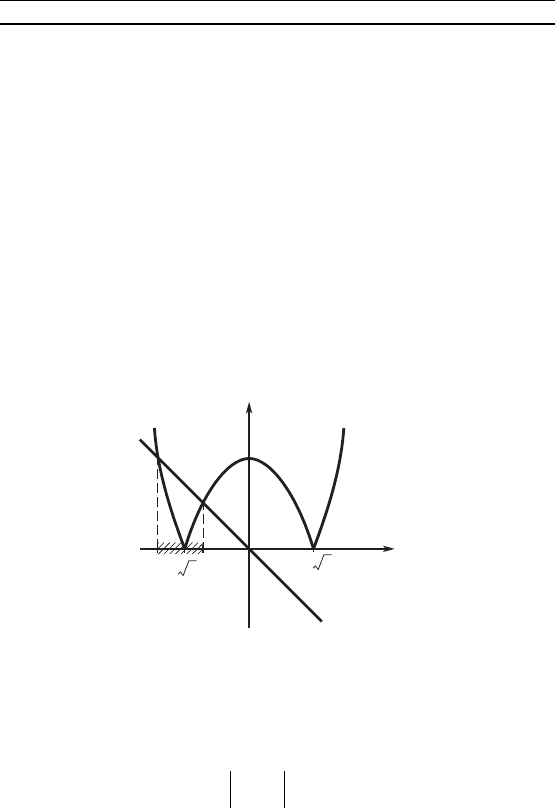
88 Г л а в а 4. Неравенства. Уравнения и неравенства с параметрами
17. < 1. 18. m 3.
19. – > x. 20. > .
21. l 2x + 3. 22. > –2.
23. + > .
24. – > 1.
Неравенства, содержащие неизвестное под знаом модля.
При решении неравенств, содержащих неизвестное под знаом
модуля, используют тот же способ, что и при решении анало-
ичных уравнений, а именно решение исходноо неравенства
сводят решению несольих неравенств, рассматриваемых на
промежутах знаопостоянства выражений, находящихся под
знаом модуля.
П р и м е р 4. Решить неравенство
|x
2
– 2| + x < 0. (*)
Р е ш е н и е. Рассмотрим промежути знаопостоянства вы-
ражения x
2
– 2, записанноо под знаом модуля.
1. Пусть x
2
– 2 l 0. Тода неравенство (*) примет вид
x
2
+ x – 2 < 0. (**)
Пересечение множества решений
неравенства (**) и неравенства
x
2
– 2 l 0 представляет собой пер-
вое множество решений исходноо
неравенства: x Ý (–2; – ] (рис. 2).
2. Пусть x
2
– 2 < 0. Тода соласно определению модуля
имеем |x
2
– 2| = 2 – x
2
, и неравенство (*) примет вид
2 – x
2
+ x < 0. (***)
Пересечение множества решений
неравенства (***) и неравенства
x
2
– 2 < 0 дает второе множество
решений исходноо неравенства:
x Ý (– ; –1) (рис. 3).
x 5+
1 x–
------------------
4 x 1+–
1 x 3+–
----------------------------
8 x
2
– 25 x
2
–
1
1 x+
------------------
1
2 x–
-------------
x
2
x–2– x
2
3x 4++
x
2
16–
x 3–
----------------------- -
x 3–
5
x 3–
----------------- -
3x
2
5x 7++ 3x
2
5x 2++
–2 0 1
x
–
2
2
Рис. 2
2
–1
02
x
–
2
2
Рис. 3
2
§ 17. Рациональные и иррациональные неравенства 89
Объединяя найденные множества решений, оончательно
получаем x Ý (–2; –1).
Ответ. x Ý (–2; –1).
В отличие от уравнений неравенства не допусают непо-
средственной провери. Однао во мноих случаях можно убе-
диться в правильности полученных результатов рафичесим
способом. Действительно, запишем неравенство из примера 4
в виде
|x
2
– 2| < –x.
Построим рафии фунций y
1
= |x
2
– 2| и y
2
= –x, входящих
в левую и правую части рассматриваемоо неравенства, и най-
дем те значения арумента, при оторых y
1
< y
2
.
На рис. 4 заштрихованная часть оси абсцисс содержит исо-
мые значения x.
Решение неравенств, содержащих зна модуля, инода
можно значительно соратить, используя равенство |x
2
| = x
2
.
П р и м е р 5. Решить неравенство
> 1. (*)
Р е ш е н и е. Исходное неравенство при всех x − –2 эвива-
лентно неравенству
|x – 1| > |x + 2|. (**)
Возведя обе части неравенства (**) в вадрат, после приве-
дения подобных членов получаем неравенство
6x < –3,
т. е. x < – 0,5.
x
O
y
y
2
= –x
–2
2
–1
–
2
2
y
1
= |x
2
– 2|
Рис. 4
x 1–
x 2+
------------- -
