Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


70 Г л а в а 3. Системы уравнений
П р и м е р 4. Решить систему уравнений
Р е ш е н и е. Это — симметричесая система. Положим
v = xy, u = x + y. Тода, используя равенство
x
2
+ y
2
= (x + y)
2
– 2xy,
получаем относительно новых неизвестных систему
единственным решением оторой является u = 6, v = 8. Возвра-
щаясь первоначальным неизвестным, сведем исходную сис-
тему более простой системе
решение оторой можно найти, используя, например, теорему
Виета.
Ответ. (2; 4), (4; 2).
Решите систему уравнений:
11. 12.
13. 14.
15. 16.
17. 18.
Используя омбинации изложенных ранее методов, решите
систему уравнений:
19.
20.
x
2
+ y
2
= 2(xy + 2),
x + y = 6.
u
2
– 2v = 2v + 4,
u = 6,
x + y = 6,
xy = 8,
x
2
y + y
2
x = 20,
+ = .
1
x
---
1
y
---
5
4
---
x
2
+ y
2
= a,
+ = b.
1
x
2
------
1
y
2
----- -
x
4
+ y
4
= 82,
x + y = 4.
x
3
+ y
3
= 9,
xy = 2.
x
3
+ y
3
= 2,
xy(x + y) = 2.
(x
2
+ y
2
)xy = 78,
x
4
+ y
4
= 97.
5(x
4
+ y
4
) = 41(x
2
+ y
2
),
x
2
+ y
2
+ xy = 13.
x
4
+ y
4
= 97,
xy = 6.
(x
2
– x + 1) (y
2
– y + 1) = 3,
(x + 1) (y + 1) = 6.
+ = ,
x
2
+ y
2
= 5.
xy+
xy–
------------- -
xy–
xy+
------------- -
10
3
------
§ 14. Системы нелинейных уравнений 71
21. 22.
23. 24.
25.
26.
27. 28.
Симметричесие системы трех уравнений с тремя неизвест-
ными x, y, z обычно решают с помощью введения новых неиз-
вестных
u = x + y + z, v = xy + yz + zx, w = xyz.
При этом удобно использовать следующие равенства:
x
2
+ y
2
+ z
2
= (x + y + z)
2
– 2(xy + yz + zx) = u
2
– 2v,
x
3
+ y
3
+ z
3
= (x + y + z)
3
–
– 3(x + y + z)(xy + yz + zx) + 3xyz = u
3
– 3uv + 3w.
П р и м е р 5. Решить систему уравнений
Р е ш е н и е. Данная система является симметричесой.
Введя вспомоательные неизвестные
x + y + z = u, xy + yz + zx = v, xyz = w
и используя равенство
x
3
+ y
3
+ z
3
= u
3
– 3uv + 3w,
получаем систему
или, возвращаясь старым неизвестным, систему
(*)
2x
3
y
2
– y
3
x
2
= 36,
2x
2
y – y
2
x = 6.
xy – x + y = 1,
x
2
y – y
2
x = 30.
xy + x – y = 3,
x
2
y – xy
2
= 2.
x
2
+ xy + x = 10,
y
2
+ xy + y = 20.
x
2
+ xy + 2y
2
= 37,
2x
2
+ 2xy + y
2
= 26.
x
2
– xy + y
2
= 19,
x
4
+ x
2
y
2
+ y
4
= 931.
(x
2
+ 1) (y
2
+ 1) = 10,
(x + y)(xy – 1) = 3.
x
5
– y
5
= 3093,
x – y = 3.
x + y + z = 1,
xy + yz + zx = –4,
x
3
+ y
3
+ z
3
= 1.
u = 1,
v = –4,
u
3
– 3uv + 3w = 1,
x + y + z = 1,
xy + yz + zx = –4,
xyz = –4.

70 Г л а в а 3. Системы уравнений
П р и м е р 4. Решить систему уравнений
Р е ш е н и е. Это — симметричесая система. Положим
v = xy, u = x + y. Тода, используя равенство
x
2
+ y
2
= (x + y)
2
– 2xy,
получаем относительно новых неизвестных систему
единственным решением оторой является u = 6, v = 8. Возвра-
щаясь первоначальным неизвестным, сведем исходную сис-
тему более простой системе
решение оторой можно найти, используя, например, теорему
Виета.
Ответ. (2; 4), (4; 2).
Решите систему уравнений:
11. 12.
13. 14.
15. 16.
17. 18.
Используя омбинации изложенных ранее методов, решите
систему уравнений:
19.
20.
x
2
+ y
2
= 2(xy + 2),
x + y = 6.
u
2
– 2v = 2v + 4,
u = 6,
x + y = 6,
xy = 8,
x
2
y + y
2
x = 20,
+ = .
1
x
---
1
y
---
5
4
---
x
2
+ y
2
= a,
+ = b.
1
x
2
------
1
y
2
----- -
x
4
+ y
4
= 82,
x + y = 4.
x
3
+ y
3
= 9,
xy = 2.
x
3
+ y
3
= 2,
xy(x + y) = 2.
(x
2
+ y
2
)xy = 78,
x
4
+ y
4
= 97.
5(x
4
+ y
4
) = 41(x
2
+ y
2
),
x
2
+ y
2
+ xy = 13.
x
4
+ y
4
= 97,
xy = 6.
(x
2
– x + 1) (y
2
– y + 1) = 3,
(x + 1) (y + 1) = 6.
+ = ,
x
2
+ y
2
= 5.
xy+
xy–
------------- -
xy–
xy+
------------- -
10
3
------
§ 14. Системы нелинейных уравнений 71
21. 22.
23. 24.
25.
26.
27. 28.
Симметричесие системы трех уравнений с тремя неизвест-
ными x, y, z обычно решают с помощью введения новых неиз-
вестных
u = x + y + z, v = xy + yz + zx, w = xyz.
При этом удобно использовать следующие равенства:
x
2
+ y
2
+ z
2
= (x + y + z)
2
– 2(xy + yz + zx) = u
2
– 2v,
x
3
+ y
3
+ z
3
= (x + y + z)
3
–
– 3(x + y + z)(xy + yz + zx) + 3xyz = u
3
– 3uv + 3w.
П р и м е р 5. Решить систему уравнений
Р е ш е н и е. Данная система является симметричесой.
Введя вспомоательные неизвестные
x + y + z = u, xy + yz + zx = v, xyz = w
и используя равенство
x
3
+ y
3
+ z
3
= u
3
– 3uv + 3w,
получаем систему
или, возвращаясь старым неизвестным, систему
(*)
2x
3
y
2
– y
3
x
2
= 36,
2x
2
y – y
2
x = 6.
xy – x + y = 1,
x
2
y – y
2
x = 30.
xy + x – y = 3,
x
2
y – xy
2
= 2.
x
2
+ xy + x = 10,
y
2
+ xy + y = 20.
x
2
+ xy + 2y
2
= 37,
2x
2
+ 2xy + y
2
= 26.
x
2
– xy + y
2
= 19,
x
4
+ x
2
y
2
+ y
4
= 931.
(x
2
+ 1) (y
2
+ 1) = 10,
(x + y)(xy – 1) = 3.
x
5
– y
5
= 3093,
x – y = 3.
x + y + z = 1,
xy + yz + zx = –4,
x
3
+ y
3
+ z
3
= 1.
u = 1,
v = –4,
u
3
– 3uv + 3w = 1,
x + y + z = 1,
xy + yz + zx = –4,
xyz = –4.

72 Г л а в а 3. Системы уравнений
Решение системы (*) можно найти с помощью теоремы
Виета для убичесоо мноочлена: орни t
1
, t
2
, t
3
убичесоо
мноочлена t
3
+ at
2
+ bt + c удовлетворяют равенствам
t
1
+ t
2
+ t
3
= –a,
t
1
t
2
+ t
1
t
3
+ t
2
t
3
= b,
t
1
t
2
t
3
= –c.
Ясно, что при a = –1, b = –4, c = 4 орни убичесоо урав-
нения
t
3
– t
2
– 4t + 4 = 0 (**)
связаны теми же равенствами, что и неизвестные x, y, z систе-
мы (*), и, следовательно, тройа значений неизвестных
x = t
1
, y = t
2
, z = t
3
есть решение системы (*). Кроме этой тройи, в силу симмет-
ричности системы решениями являются таже следующие трой-
и значений неизвестных:
x = t
2
, y = t
1
, z = t
3
,
x = t
3
, y = t
2
, z = t
1
,
x = t
1
, y = t
3
, z = t
2
,
x = t
2
, y = t
3
, z = t
1
,
x = t
3
, y = t
1
, z = t
2
.
Таим образом, решение данной системы сводится нахож-
дению орней убичесоо уравнения (**); ими являются чис-
ла t
1
= 2, t
2
= –2, t
3
= 1.
Ита, решения исходной системы — это следующие упорядо-
ченные тройи чисел: (2; –2; 1); (–2; 2, 1); (1; 2; –2); (–2; 1; 2);
(1; –2; 2); (2; 1; –2).
Ответ. (2; –2; 1); (–2; 2, 1); (1; 2; –2); (–2; 1; 2); (1; –2; 2);
(2; 1; –2).
Решите систему уравнений:
29. 30.
Инода системы трех уравнений с тремя неизвестными ре-
шают с помощью введения вспомоательных неизвестных.
x + y + z = 0,
x
2
+ y
2
+ z
2
= x
3
+ y
3
+ z
3
,
xyz = 2.
x + y + z = 1,
x
2
+ y
2
+ z
2
= 1,
x
3
+ y
3
+ z
3
= 1.
§ 14. Системы нелинейных уравнений 73
П р и м е р 6. Решить систему уравнений
Р е ш е н и е. Данная система равносильна системе
или
(мы разделили почленно левые части уравнений). Полаая = u,
= v, = w, получаем линейную систему относительно новых
неизвестных:
Ее решение есть тройа чисел ; ; . Ита, решени-
ем исходной системы является тройа чисел ; ; .
Ответ.; ; .
В отличие от систем линейных уравнений системы нелиней-
ных уравнений моут быть определенными даже в тех случаях,
ода число уравнений меньше чисел неизвестных. Простей-
ший пример таой системы представляет собой система, состоя-
щая из одноо уравнения
(x – 1)
2
+ (y – 2)
2
+ (z – 3)
2
= 0,
единственным решением отороо является x = 1, y = 2, z = 3.
= 5,
= 3,
= 4.
3xy
xy+
------------- -
2xz
xz+
-------------
yz
yz+
-------------
= ,
= ,
= ,
xy+
xy
------------- -
3
5
---
xz+
xz
-------------
2
3
---
yz+
yz
-------------
1
4
---
+ = ,
+ = ,
+ =
1
y
---
1
x
---
3
5
---
1
x
---
1
z
---
2
3
---
1
y
---
1
z
---
1
4
---
1
x
---
1
y
---
1
z
---
u + v = ,
u + w = ,
w + v = .
3
5
---
2
3
---
1
4
---
61
120
----------
11
120
----------
19
120
----------
120
61
----------
120
11
----------
120
19
----------
120
61
----------
120
11
----------
120
19
----------
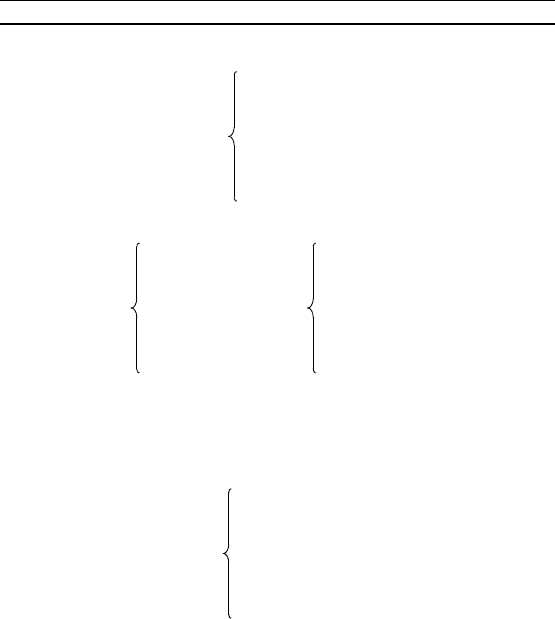
72 Г л а в а 3. Системы уравнений
Решение системы (*) можно найти с помощью теоремы
Виета для убичесоо мноочлена: орни t
1
, t
2
, t
3
убичесоо
мноочлена t
3
+ at
2
+ bt + c удовлетворяют равенствам
t
1
+ t
2
+ t
3
= –a,
t
1
t
2
+ t
1
t
3
+ t
2
t
3
= b,
t
1
t
2
t
3
= –c.
Ясно, что при a = –1, b = –4, c = 4 орни убичесоо урав-
нения
t
3
– t
2
– 4t + 4 = 0 (**)
связаны теми же равенствами, что и неизвестные x, y, z систе-
мы (*), и, следовательно, тройа значений неизвестных
x = t
1
, y = t
2
, z = t
3
есть решение системы (*). Кроме этой тройи, в силу симмет-
ричности системы решениями являются таже следующие трой-
и значений неизвестных:
x = t
2
, y = t
1
, z = t
3
,
x = t
3
, y = t
2
, z = t
1
,
x = t
1
, y = t
3
, z = t
2
,
x = t
2
, y = t
3
, z = t
1
,
x = t
3
, y = t
1
, z = t
2
.
Таим образом, решение данной системы сводится нахож-
дению орней убичесоо уравнения (**); ими являются чис-
ла t
1
= 2, t
2
= –2, t
3
= 1.
Ита, решения исходной системы — это следующие упорядо-
ченные тройи чисел: (2; –2; 1); (–2; 2, 1); (1; 2; –2); (–2; 1; 2);
(1; –2; 2); (2; 1; –2).
Ответ. (2; –2; 1); (–2; 2, 1); (1; 2; –2); (–2; 1; 2); (1; –2; 2);
(2; 1; –2).
Решите систему уравнений:
29. 30.
Инода системы трех уравнений с тремя неизвестными ре-
шают с помощью введения вспомоательных неизвестных.
x + y + z = 0,
x
2
+ y
2
+ z
2
= x
3
+ y
3
+ z
3
,
xyz = 2.
x + y + z = 1,
x
2
+ y
2
+ z
2
= 1,
x
3
+ y
3
+ z
3
= 1.
§ 14. Системы нелинейных уравнений 73
П р и м е р 6. Решить систему уравнений
Р е ш е н и е. Данная система равносильна системе
или
(мы разделили почленно левые части уравнений). Полаая = u,
= v, = w, получаем линейную систему относительно новых
неизвестных:
Ее решение есть тройа чисел ; ; . Ита, решени-
ем исходной системы является тройа чисел ; ; .
Ответ.; ; .
В отличие от систем линейных уравнений системы нелиней-
ных уравнений моут быть определенными даже в тех случаях,
ода число уравнений меньше чисел неизвестных. Простей-
ший пример таой системы представляет собой система, состоя-
щая из одноо уравнения
(x – 1)
2
+ (y – 2)
2
+ (z – 3)
2
= 0,
единственным решением отороо является x = 1, y = 2, z = 3.
= 5,
= 3,
= 4.
3xy
xy+
------------- -
2xz
xz+
-------------
yz
yz+
-------------
= ,
= ,
= ,
xy+
xy
------------- -
3
5
---
xz+
xz
-------------
2
3
---
yz+
yz
-------------
1
4
---
+ = ,
+ = ,
+ =
1
y
---
1
x
---
3
5
---
1
x
---
1
z
---
2
3
---
1
y
---
1
z
---
1
4
---
1
x
---
1
y
---
1
z
---
u + v = ,
u + w = ,
w + v = .
3
5
---
2
3
---
1
4
---
61
120
----------
11
120
----------
19
120
----------
120
61
----------
120
11
----------
120
19
----------
120
61
----------
120
11
----------
120
19
----------

74 Г л а в а 3. Системы уравнений
П р и м е р 7. Решить систему уравнений
Р е ш е н и е. Возведя обе части первоо уравнения в вадрат,
имеем
x
2
+ y
2
+ z
2
+ 2xy + 2yz + 2zx = 16. (*)
Вычитая из уравнения (*) второе уравнение системы, полу-
чаем уравнение
x
2
+ y
2
+ 2z
2
+ 2yz + 2zx = 0,
оторое можно записать в виде
(x + z)
2
+ (y + z)
2
= 0.
Последнее уравнение выполняется тольо при x = –z, y = –z.
Возвращаясь исходной системе, находим из первоо урав-
нения z = –4 и, следовательно, x = 4, y = 4.
Полученное решение (4; 4; –4) и является решением исход-
ной системы.
Ответ. (4; 4; –4).
Решите систему уравнений:
31. 32.
33. 34.
35. 36.
37. 38.
39.
x + y + z = 4,
2xy – z
2
= 16.
y
2
+ xy – z
2
= 4,
x + 5y = 8.
x
2
– 2yz = –1,
y + z – x = 1.
3xy – = –5,
xy + = –5,
yz – = 1.
16
xz
------ -
8
yz
------
3
xy
-------
x + y = ,
x + z = ,
y + z = .
xy
1 xy+
----------------- -
xz
1 xz+
-----------------
yz
1 yz+
-----------------
x
2
– (y – z)
2
= a,
y
2
– (z – x)
2
= b,
z
2
– (x – y)
2
= c.
= a,
= b,
= c.
xyz
yz+
-------------
xyz
zx+
-------------
xyz
xy+
------------- -
x + y + z = 13,
x
2
+ y
2
+ z
2
= 91,
y
2
= xz.
xy + yz + zx = 11,
x
2
+ y
2
+ z
2
= 14,
xyz = 6.
x + y + z = 0,
x
2
+ y
2
+ z
2
= 2(y – x – z) –2,
x
3
+ y
3
+ z
3
= 3(x
2
– y
2
+ z
2
).
§ 14. Системы нелинейных уравнений 75
40.
41. 42.
43. 44.
45. 46.
47. 48.
Системы, содержащие иррациональное равнение. Если
среди уравнений системы имеются иррациональные, то для ее
решения обычно освобождаются от иррациональности. При
этом используют те же методы, что и для решения иррацио-
нальных уравнений.
П р и м е р 8. Решить систему уравнений
Р е ш е н и е. Полаая = u и = v, получаем
симметричесую систему нелинейных уравнений
(*)
решения оторой u = 2, v = 1 и u = 1, v = 2. Возвращаясь ис-
ходным неизвестным, приходим двум системам линейных
уравнений:
Первая система имеет решение x = 3, y = 4, а вторая — ре-
шение x = 0, y = –11.
Ответ. (3; 4); (0; –11).
x + y + z = 1,
4x
2
+ y
2
+ z
2
– 5x = x
3
+ y
3
+ z
3
– 2,
xyz = 2 + yz.
2(x + y) = xy,
xy + yz + zx = 108,
xyz = 180.
x(x + y + z) = a,
y(x + y + z) = b,
z(x + y + z) = c.
x
2
+ y
2
= axyz,
y
2
+ z
2
= bxyz,
z
2
+ x
2
= cxyz.
x
2
y = x + y – z,
z
2
x = x – y + z,
y
2
x = y – x + z.
4xy + x
2
+ y
2
= 1,
8xz + x
2
+ 4z
2
= –2,
8yz + y
2
+ 4z
2
= 1.
2(x
2
+ y
2
) = xyz,
10(y
2
+ z
2
) = 29xyz,
5(z
2
+ x
2
) = 13xyz.
xyz
2
= –y – 2x,
2x
2
yz = –y – z,
3xy
2
z = 2x – z.
xy + x + y = 7,
yz + y + z = –3,
zx + x + z = –5.
+ = 3,
5x – y = 11.
15x+
4
5 y–
4
15x+
4
5 y–
4
u + v = 3,
u
4
+ v
4
= 17,
1 + 5x = 16,
5 – y = 1,
1 + 5x = 1,
5 – y = 16.
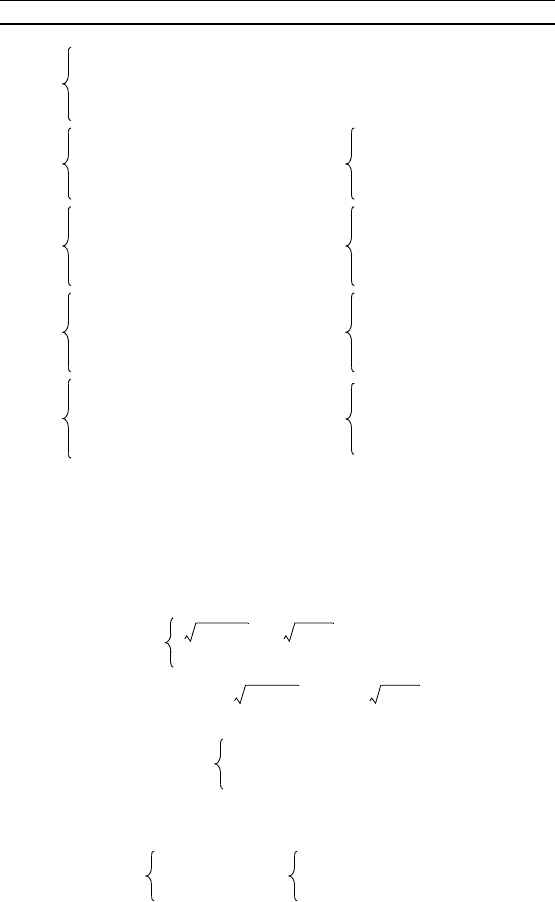
74 Г л а в а 3. Системы уравнений
П р и м е р 7. Решить систему уравнений
Р е ш е н и е. Возведя обе части первоо уравнения в вадрат,
имеем
x
2
+ y
2
+ z
2
+ 2xy + 2yz + 2zx = 16. (*)
Вычитая из уравнения (*) второе уравнение системы, полу-
чаем уравнение
x
2
+ y
2
+ 2z
2
+ 2yz + 2zx = 0,
оторое можно записать в виде
(x + z)
2
+ (y + z)
2
= 0.
Последнее уравнение выполняется тольо при x = –z, y = –z.
Возвращаясь исходной системе, находим из первоо урав-
нения z = –4 и, следовательно, x = 4, y = 4.
Полученное решение (4; 4; –4) и является решением исход-
ной системы.
Ответ. (4; 4; –4).
Решите систему уравнений:
31. 32.
33. 34.
35. 36.
37. 38.
39.
x + y + z = 4,
2xy – z
2
= 16.
y
2
+ xy – z
2
= 4,
x + 5y = 8.
x
2
– 2yz = –1,
y + z – x = 1.
3xy – = –5,
xy + = –5,
yz – = 1.
16
xz
------ -
8
yz
------
3
xy
-------
x + y = ,
x + z = ,
y + z = .
xy
1 xy+
----------------- -
xz
1 xz+
-----------------
yz
1 yz+
-----------------
x
2
– (y – z)
2
= a,
y
2
– (z – x)
2
= b,
z
2
– (x – y)
2
= c.
= a,
= b,
= c.
xyz
yz+
-------------
xyz
zx+
-------------
xyz
xy+
------------- -
x + y + z = 13,
x
2
+ y
2
+ z
2
= 91,
y
2
= xz.
xy + yz + zx = 11,
x
2
+ y
2
+ z
2
= 14,
xyz = 6.
x + y + z = 0,
x
2
+ y
2
+ z
2
= 2(y – x – z) –2,
x
3
+ y
3
+ z
3
= 3(x
2
– y
2
+ z
2
).
§ 14. Системы нелинейных уравнений 75
40.
41. 42.
43. 44.
45. 46.
47. 48.
Системы, содержащие иррациональное равнение. Если
среди уравнений системы имеются иррациональные, то для ее
решения обычно освобождаются от иррациональности. При
этом используют те же методы, что и для решения иррацио-
нальных уравнений.
П р и м е р 8. Решить систему уравнений
Р е ш е н и е. Полаая = u и = v, получаем
симметричесую систему нелинейных уравнений
(*)
решения оторой u = 2, v = 1 и u = 1, v = 2. Возвращаясь ис-
ходным неизвестным, приходим двум системам линейных
уравнений:
Первая система имеет решение x = 3, y = 4, а вторая — ре-
шение x = 0, y = –11.
Ответ. (3; 4); (0; –11).
x + y + z = 1,
4x
2
+ y
2
+ z
2
– 5x = x
3
+ y
3
+ z
3
– 2,
xyz = 2 + yz.
2(x + y) = xy,
xy + yz + zx = 108,
xyz = 180.
x(x + y + z) = a,
y(x + y + z) = b,
z(x + y + z) = c.
x
2
+ y
2
= axyz,
y
2
+ z
2
= bxyz,
z
2
+ x
2
= cxyz.
x
2
y = x + y – z,
z
2
x = x – y + z,
y
2
x = y – x + z.
4xy + x
2
+ y
2
= 1,
8xz + x
2
+ 4z
2
= –2,
8yz + y
2
+ 4z
2
= 1.
2(x
2
+ y
2
) = xyz,
10(y
2
+ z
2
) = 29xyz,
5(z
2
+ x
2
) = 13xyz.
xyz
2
= –y – 2x,
2x
2
yz = –y – z,
3xy
2
z = 2x – z.
xy + x + y = 7,
yz + y + z = –3,
zx + x + z = –5.
+ = 3,
5x – y = 11.
15x+
4
5 y–
4
15x+
4
5 y–
4
u + v = 3,
u
4
+ v
4
= 17,
1 + 5x = 16,
5 – y = 1,
1 + 5x = 1,
5 – y = 16.
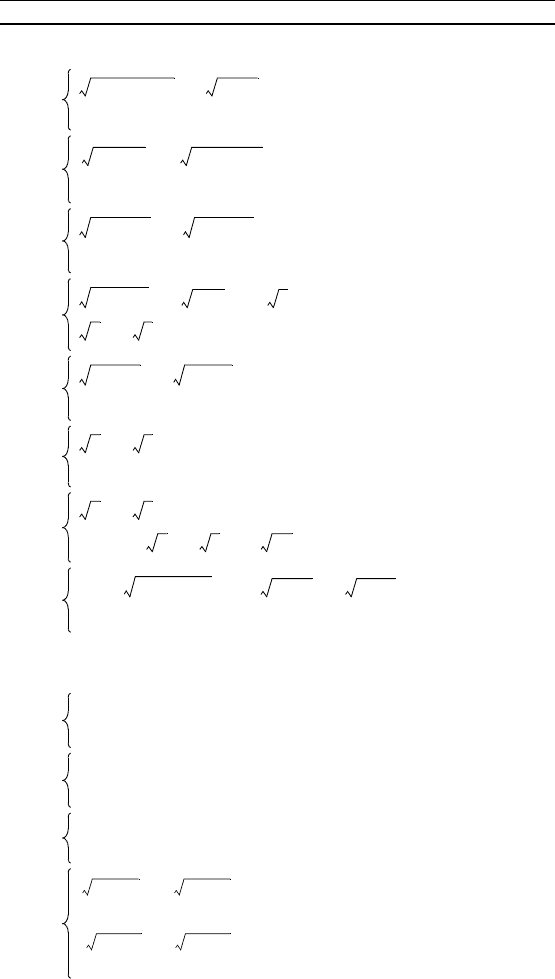
76 Г л а в а 3. Системы уравнений
Решите систему уравнений:
49.
50.
51.
52.
53.
54.
55.
56.
Используя изложенные ранее методы, решите систему урав-
нений:
57.
58.
59.
60.
– = 1,
3x + 2y = 4.
2xy1++
xy+
+ = 3,
2x + y = 7.
x 2y+
3
xy–2+
3
+ = 3(x – y),
x
2
– y
2
= 41.
x
2
xy– xy y
2
–
+ = 8 ,
+ = 4.
x
2
y
2
+ 2xy 2
x y
+ = 5,
x
2
+ y
2
= 13.
x
2
5+ y
2
5–
+ = 2,
x – 2y + 1 = 0.
x y
+ = 8,
x + y – + – 2 = 2.
x y
x y xy
xy + = 8( + ),
(x + y)
3/2
– (x – y)
3/2
= 26.
x
2
y
2
y
4
– xy+ xy–
3x
2
+ 2xy + y
2
= 11,
x
2
+ 2xy + 3y
2
= 17.
x
2
+ xy + y
2
= 19(x – y)
2
,
x
2
– xy + y
2
= 7(x – y).
(x – 1)
2
+ (y + 1)
2
– z
2
= 0,
x – z – 1 = 0.
+ = ,
– = .
2xy+
3
y
---------------------- -
2xy+
3
2x
---------------------- -
81
182
----------
2xy–
3
y
----------------------
2xy–
3
2x
----------------------
1
182
----------
§ 15. Системы показательных и логарифмических уравнений 77
61. 62.
§ 15. Системы показательных
и логарифмических уравнений
Для решения системы, содержащей поазательное или лоа-
рифмичесое уравнение, обычно сводят поазательное (или ло-
арифмичесое) уравнение алебраичесому уравнению, а за-
тем решают полученную алебраичесую систему.
П р и м е р 1. Решить систему уравнений
Р е ш е н и е. Множество допустимых значений неизвестных
x и y определяется системой неравенств
(*)
Из поазательноо уравнения исходной системы, записанноо
в виде
=
следует, что
x – y + 6 = 6 – 2y;
из лоарифмичесоо уравнения, записанноо в виде
log
3
((x – 2y)(3x + 2y)) = 3,
следует, что
(x – 2y)(3x + 2y) = 27.
Таим образом, решение исходной системы сводится ре-
шению системы уравнений
(**)
рассматриваемой на множестве допустимых значений неиз-
вестных, задаваемом системой (*). Выражая y из первоо урав-
нения системы (**) и подставляя y = –x во второе уравнение,
получаем уравнение 3x
2
= 27, решениями отороо являются
x
1
= 3, x
2
= –3. Из первоо уравнения системы (**) находим
x + y – z = 2,
x
2
+ y
2
+ z
2
= 6,
x
3
+ y
3
– z
3
= 8.
x
2
+ xy + y
2
= 1,
y
2
+ yz + z
2
= 3,
x
2
+ xz + z
2
= 7.
8 =
log
3
(x – 2y) + log
3
(3x + 2y) = 3.
(2)
xy–
0,5
y 3–
,
x – 2y > 0,
3x + 2y > 0.
(2)
xy–6+
(2)
62y–
,
x – y + 6 = 6 – 2y,
(x – 2y)(3x + 2y) = 27,
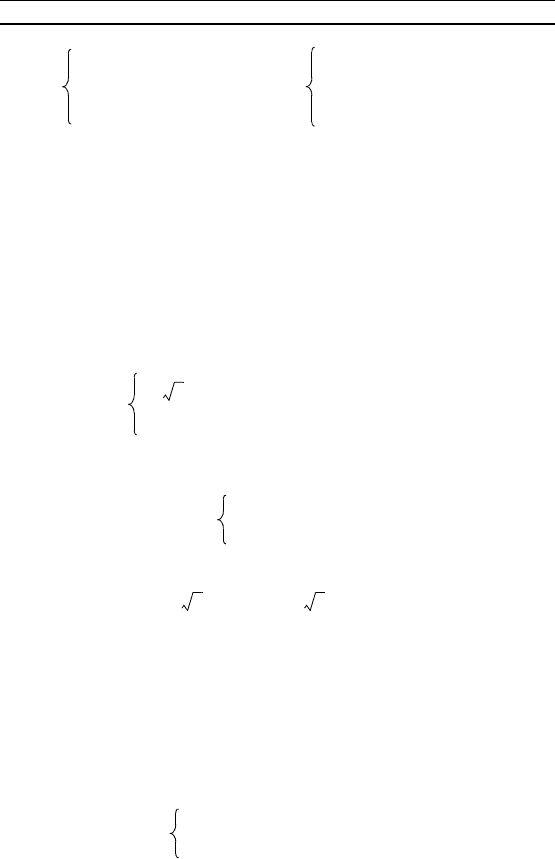
76 Г л а в а 3. Системы уравнений
Решите систему уравнений:
49.
50.
51.
52.
53.
54.
55.
56.
Используя изложенные ранее методы, решите систему урав-
нений:
57.
58.
59.
60.
– = 1,
3x + 2y = 4.
2xy1++
xy+
+ = 3,
2x + y = 7.
x 2y+
3
xy–2+
3
+ = 3(x – y),
x
2
– y
2
= 41.
x
2
xy– xy y
2
–
+ = 8 ,
+ = 4.
x
2
y
2
+ 2xy 2
x y
+ = 5,
x
2
+ y
2
= 13.
x
2
5+ y
2
5–
+ = 2,
x – 2y + 1 = 0.
x y
+ = 8,
x + y – + – 2 = 2.
x y
x y xy
xy + = 8( + ),
(x + y)
3/2
– (x – y)
3/2
= 26.
x
2
y
2
y
4
– xy+ xy–
3x
2
+ 2xy + y
2
= 11,
x
2
+ 2xy + 3y
2
= 17.
x
2
+ xy + y
2
= 19(x – y)
2
,
x
2
– xy + y
2
= 7(x – y).
(x – 1)
2
+ (y + 1)
2
– z
2
= 0,
x – z – 1 = 0.
+ = ,
– = .
2xy+
3
y
---------------------- -
2xy+
3
2x
---------------------- -
81
182
----------
2xy–
3
y
----------------------
2xy–
3
2x
----------------------
1
182
----------
§ 15. Системы показательных и логарифмических уравнений 77
61. 62.
§ 15. Системы показательных
и логарифмических уравнений
Для решения системы, содержащей поазательное или лоа-
рифмичесое уравнение, обычно сводят поазательное (или ло-
арифмичесое) уравнение алебраичесому уравнению, а за-
тем решают полученную алебраичесую систему.
П р и м е р 1. Решить систему уравнений
Р е ш е н и е. Множество допустимых значений неизвестных
x и y определяется системой неравенств
(*)
Из поазательноо уравнения исходной системы, записанноо
в виде
=
следует, что
x – y + 6 = 6 – 2y;
из лоарифмичесоо уравнения, записанноо в виде
log
3
((x – 2y)(3x + 2y)) = 3,
следует, что
(x – 2y)(3x + 2y) = 27.
Таим образом, решение исходной системы сводится ре-
шению системы уравнений
(**)
рассматриваемой на множестве допустимых значений неиз-
вестных, задаваемом системой (*). Выражая y из первоо урав-
нения системы (**) и подставляя y = –x во второе уравнение,
получаем уравнение 3x
2
= 27, решениями отороо являются
x
1
= 3, x
2
= –3. Из первоо уравнения системы (**) находим
x + y – z = 2,
x
2
+ y
2
+ z
2
= 6,
x
3
+ y
3
– z
3
= 8.
x
2
+ xy + y
2
= 1,
y
2
+ yz + z
2
= 3,
x
2
+ xz + z
2
= 7.
8 =
log
3
(x – 2y) + log
3
(3x + 2y) = 3.
(2)
xy–
0,5
y 3–
,
x – 2y > 0,
3x + 2y > 0.
(2)
xy–6+
(2)
62y–
,
x – y + 6 = 6 – 2y,
(x – 2y)(3x + 2y) = 27,

78 Г л а в а 3. Системы уравнений
y
1
= –3, y
2
= 3. Однао из двух найденных пар чисел (3; –3),
(–3; 3) решений системы (**) лишь пара (3; –3) удовлетворяет
системе неравенств (*).
Ответ. (3; –3).
Решите систему уравнений:
1. 2.
3. 4.
5.
6.
7.
8.
9.
10. 11.
12.
13.
log
y
x + log
x
y = 2,
x
2
– y = 20.
log
4
x – log
2
y = 0,
x
2
– 2y
2
– 8 = 0.
= ,
= y
4
– 5.
4
xy+
2
yx–
4
log
2
x
+ = 12,
+
=
.
x
2
y
------
y
2
x
----- -
2
log
2
x–
5
log
5
(1/y)
1
3
---
x + y = 12,
2(2 log
y
x – log
1/x
y) = 5.
– 7 · = ,
y – x = 3.
4
x
2
x
y
2
---
–
2
3 y–
3 + 7 – 6 = 0,
lg (3x – y) + lg (x + y) – 4lg2 = 0.
2
3
---
2xy–
2
3
---
2xy–()/2
= 32,
log
3
(x – y) = 1 – log
3
(x + y).
4
x
y
---
y
x
---
+
– 27 · = 0,
lg x + lg y = lg (4 – ).
9
xy
2
4
3
y
1
4
---
1
2
---
x
4
· = 1152,
(x + y) = 2.
3
x–
2
y
log
5
· = 6,
· = 12.
2
x
3
y
3
x
4
y
= 1,
lg (x + y) – 1 = lg 6 – lg (x + 2y).
(0,48
x
2
2+
)
2xy–
= 1,
x – y = 2.
x
x
2
y
2
–16–
§ 15. Системы показательных и логарифмических уравнений 79
Если основание степени в поазательном уравнении систе-
мы является фунцией неизвестных, то таую систему можно
свести системе рациональных уравнений, принимая в ачест-
ве одноо из неизвестных лоарифм этой фунции по неоторо-
му основанию.
П р и м е р 2. Решить систему уравнений
Р е ш е н и е. Лоарифмируя оба уравнения системы по ос-
нованию 5, получаем эвивалентную исходной систему
Положим log
5
x = z и получим систему рациональных уравнений
(*)
Выразив z из первоо уравнения системы (*) и подставив во
второе, придем уравнению
= 3,
имеющему решения y
1
= 1, y
2
= –1. Из первоо уравнения сис-
темы (*) находим (а при y = 1, та и при y = –1), что z = 1.
Тода из уравнения log
5
x = 1 получаем x = 5. Таим образом,
решениями исходной системы являются две пары чисел: (5; 1)
и (5; –1).
Ответ. (5; 1); (5; –1).
Решите систему уравнений:
14. 15.
16. 17.
18. 19.
= 5,
= 125.
x
2y
2
1–
x
y
2
2+
(2y
2
– 1) log
5
x = 1,
(y
2
+ 2) log
5
x = 3.
(2y
2
– 1)z = 1,
(y
2
+ 2)z = 3.
y
2
2+
2y
2
1–
------------------- -
y = 1 + log
4
x,
x
y
= 4
6
.
y – log
3
x = 1,
x
y
= 3
12
.
(x + y)3
y – x
= ,
3log
5
(x + y) = x – y.
5
27
------
x
x – 2y
= 36,
4(x – 2y) + log
6
x = 9.
(x + y) · = 6,25,
= 5.
2
y 2x–
(xy)+
1
2xy–
-----------------
lg = 1,
lg y – lg |x| = lg 2.
(xy)
2
+

78 Г л а в а 3. Системы уравнений
y
1
= –3, y
2
= 3. Однао из двух найденных пар чисел (3; –3),
(–3; 3) решений системы (**) лишь пара (3; –3) удовлетворяет
системе неравенств (*).
Ответ. (3; –3).
Решите систему уравнений:
1. 2.
3. 4.
5.
6.
7.
8.
9.
10. 11.
12.
13.
log
y
x + log
x
y = 2,
x
2
– y = 20.
log
4
x – log
2
y = 0,
x
2
– 2y
2
– 8 = 0.
= ,
= y
4
– 5.
4
xy+
2
yx–
4
log
2
x
+ = 12,
+
=
.
x
2
y
------
y
2
x
----- -
2
log
2
x–
5
log
5
(1/y)
1
3
---
x + y = 12,
2(2 log
y
x – log
1/x
y) = 5.
– 7 · = ,
y – x = 3.
4
x
2
x
y
2
---
–
2
3 y–
3 + 7 – 6 = 0,
lg (3x – y) + lg (x + y) – 4lg2 = 0.
2
3
---
2xy–
2
3
---
2xy–()/2
= 32,
log
3
(x – y) = 1 – log
3
(x + y).
4
x
y
---
y
x
---
+
– 27 · = 0,
lg x + lg y = lg (4 – ).
9
xy
2
4
3
y
1
4
---
1
2
---
x
4
· = 1152,
(x + y) = 2.
3
x–
2
y
log
5
· = 6,
· = 12.
2
x
3
y
3
x
4
y
= 1,
lg (x + y) – 1 = lg 6 – lg (x + 2y).
(0,48
x
2
2+
)
2xy–
= 1,
x – y = 2.
x
x
2
y
2
–16–
§ 15. Системы показательных и логарифмических уравнений 79
Если основание степени в поазательном уравнении систе-
мы является фунцией неизвестных, то таую систему можно
свести системе рациональных уравнений, принимая в ачест-
ве одноо из неизвестных лоарифм этой фунции по неоторо-
му основанию.
П р и м е р 2. Решить систему уравнений
Р е ш е н и е. Лоарифмируя оба уравнения системы по ос-
нованию 5, получаем эвивалентную исходной систему
Положим log
5
x = z и получим систему рациональных уравнений
(*)
Выразив z из первоо уравнения системы (*) и подставив во
второе, придем уравнению
= 3,
имеющему решения y
1
= 1, y
2
= –1. Из первоо уравнения сис-
темы (*) находим (а при y = 1, та и при y = –1), что z = 1.
Тода из уравнения log
5
x = 1 получаем x = 5. Таим образом,
решениями исходной системы являются две пары чисел: (5; 1)
и (5; –1).
Ответ. (5; 1); (5; –1).
Решите систему уравнений:
14. 15.
16. 17.
18. 19.
= 5,
= 125.
x
2y
2
1–
x
y
2
2+
(2y
2
– 1) log
5
x = 1,
(y
2
+ 2) log
5
x = 3.
(2y
2
– 1)z = 1,
(y
2
+ 2)z = 3.
y
2
2+
2y
2
1–
------------------- -
y = 1 + log
4
x,
x
y
= 4
6
.
y – log
3
x = 1,
x
y
= 3
12
.
(x + y)3
y – x
= ,
3log
5
(x + y) = x – y.
5
27
------
x
x – 2y
= 36,
4(x – 2y) + log
6
x = 9.
(x + y) · = 6,25,
= 5.
2
y 2x–
(xy)+
1
2xy–
-----------------
lg = 1,
lg y – lg |x| = lg 2.
(xy)
2
+
