Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


60 Г л а в а 2. Уравнения
Решите уравнение:
43. (x + 1) + 4x log
3
x – 16 = 0.
44. 3x
2
– 2x
3
= log
2
(x
2
+ 1) – log
2
x.
45. = 10 – log
2
x.
46. + (x – 1) log
2
x = 6 – 2x.
§ 12. Разные задачи
Решите уравнение:
1. = · . 2. + = 8 · .
3. – = 1. 4. + = 1.
5. = 2 · . 6. = .
7. = 100. 8. = ( )
x
.
9. + = – .
10. 10
(x + 1)(3x + 4)
– 2 · 10
(x + 1)(x + 2)
= .
11. – 5 · + 6 · = 0.
12. log
3
[(x + 2)(x – 3)] = 4 log
x
(2x + 1) – 7.
13. lg
2
x
3
– 20 lg + 1 = 0.
14. |1 – log
1/6
x| + 2 = |3 – log
1/6
x|.
15. (x + |x – 2|) = log
x
(5x – 6 + 5|x – 2|).
16. log
x + 1
(x
2
+ x – 6)
2
= 4.
17. = 1.
18. log
5
[ – ] = – 3 log
1/5
2.
19. 5 · + 4 · 5
cos 2x
= .
20. + = .
21. = .
log
3
2
x
3
x
log
2
2
x
12
2x 4+
3
3x
4
x 8+
2
x
4
(x 1)/2+
3
x/3
2
x
3
x/2
(sin 1)
x
(cos 1)
x
10
x
2
100
x
x
x
( x)
x
5
x
8
x
x 1+
x
x
2
3
x
11
3x 2–
13
3x 2–
13
3x 1–
11
3x 1–
10
1 x– x
2
–
9
x
12
x
16
x
log
7
x
log
x
1log
2
x 4–()+
log
2
x 3+ x 3––()
----------------------------------------------------------------
(2 5+)
x
(5 2)
x
–
1
2
---
1
25
------
sin
2
x
25
1
2
---
sin 2x
743+()
cos x
743–()
cos x
5
2
---
1
3
---
log
9
x
2
2x 4++()
6
log
1/6
x 2+()
Глава 3
Системы уравнений
Несольо уравнений
F
1
(x
1
, x
2
, ..., x
n
) = 0, F
2
(x
1
, x
2
, ..., x
n
) = 0, ...,
F
k
(x
1
, x
2
, ..., x
n
) = 0,
рассматриваемых совместно, называют системой равнений.
Решением этой системы называют упорядоченный набор зна-
чений неизвестных, обращающий все уравнения системы в тож-
дества.
Если система уравнений имеет решения, то оворят, что она
совместна. Если же система уравнений не имеет решений, то
оворят, что она несовместна.
Линейным равнением с n неизвестными называют урав-
нение вида
a
1
x
1
+ a
2
x
2
+ ... + a
n
x
n
= b,
де a
1
, a
2
, ..., a
n
, b— неоторые числа.
Систему уравнений называют линейной, если все уравне-
ния системы линейные. Совместную систему уравнений назы-
вают определенной, если она имеет единственное решение
(т. е. существует единственный набор чисел k
1
, ..., k
n
, обра-
щающий все уравнения системы в тождества).
Совместную систему уравнений называют неопределенной,
если она имеет более одноо решения. Две совместные системы
уравнений называют эвивалентными, если множества их ре-
шений совпадают.
При решении систем уравнений часто используют следую-
щие преобразования системы, приводящие системе уравне-
ний, эвивалентной исходной.
1.Если обе части аоо-либо уравнения системы умно-
жить на одно и то же (не равное нулю) число, то полученная
система будет эвивалентна первоначальной (т. е. они или обе
несовместны, или же обе совместны и множества их решений
совпадают).
2.Если обе части аоо-либо уравнения системы, умно-
женные на неоторое (отличное от нуля) число, вычесть из со-
ответствующих частей друоо уравнения и составить систему,
в оторой одно из упомянутых уравнений заменено уравнени-

60 Г л а в а 2. Уравнения
Решите уравнение:
43. (x + 1) + 4x log
3
x – 16 = 0.
44. 3x
2
– 2x
3
= log
2
(x
2
+ 1) – log
2
x.
45. = 10 – log
2
x.
46. + (x – 1) log
2
x = 6 – 2x.
§ 12. Разные задачи
Решите уравнение:
1. = · . 2. + = 8 · .
3. – = 1. 4. + = 1.
5. = 2 · . 6. = .
7. = 100. 8. = ( )
x
.
9. + = – .
10. 10
(x + 1)(3x + 4)
– 2 · 10
(x + 1)(x + 2)
= .
11. – 5 · + 6 · = 0.
12. log
3
[(x + 2)(x – 3)] = 4 log
x
(2x + 1) – 7.
13. lg
2
x
3
– 20 lg + 1 = 0.
14. |1 – log
1/6
x| + 2 = |3 – log
1/6
x|.
15. (x + |x – 2|) = log
x
(5x – 6 + 5|x – 2|).
16. log
x + 1
(x
2
+ x – 6)
2
= 4.
17. = 1.
18. log
5
[ – ] = – 3 log
1/5
2.
19. 5 · + 4 · 5
cos 2x
= .
20. + = .
21. = .
log
3
2
x
3
x
log
2
2
x
12
2x 4+
3
3x
4
x 8+
2
x
4
(x 1)/2+
3
x/3
2
x
3
x/2
(sin 1)
x
(cos 1)
x
10
x
2
100
x
x
x
( x)
x
5
x
8
x
x 1+
x
x
2
3
x
11
3x 2–
13
3x 2–
13
3x 1–
11
3x 1–
10
1 x– x
2
–
9
x
12
x
16
x
log
7
x
log
x
1log
2
x 4–()+
log
2
x 3+ x 3––()
----------------------------------------------------------------
(2 5+)
x
(5 2)
x
–
1
2
---
1
25
------
sin
2
x
25
1
2
---
sin 2x
743+()
cos x
743–()
cos x
5
2
---
1
3
---
log
9
x
2
2x 4++()
6
log
1/6
x 2+()
Глава 3
Системы уравнений
Несольо уравнений
F
1
(x
1
, x
2
, ..., x
n
) = 0, F
2
(x
1
, x
2
, ..., x
n
) = 0, ...,
F
k
(x
1
, x
2
, ..., x
n
) = 0,
рассматриваемых совместно, называют системой равнений.
Решением этой системы называют упорядоченный набор зна-
чений неизвестных, обращающий все уравнения системы в тож-
дества.
Если система уравнений имеет решения, то оворят, что она
совместна. Если же система уравнений не имеет решений, то
оворят, что она несовместна.
Линейным равнением с n неизвестными называют урав-
нение вида
a
1
x
1
+ a
2
x
2
+ ... + a
n
x
n
= b,
де a
1
, a
2
, ..., a
n
, b— неоторые числа.
Систему уравнений называют линейной, если все уравне-
ния системы линейные. Совместную систему уравнений назы-
вают определенной, если она имеет единственное решение
(т. е. существует единственный набор чисел k
1
, ..., k
n
, обра-
щающий все уравнения системы в тождества).
Совместную систему уравнений называют неопределенной,
если она имеет более одноо решения. Две совместные системы
уравнений называют эвивалентными, если множества их ре-
шений совпадают.
При решении систем уравнений часто используют следую-
щие преобразования системы, приводящие системе уравне-
ний, эвивалентной исходной.
1.Если обе части аоо-либо уравнения системы умно-
жить на одно и то же (не равное нулю) число, то полученная
система будет эвивалентна первоначальной (т. е. они или обе
несовместны, или же обе совместны и множества их решений
совпадают).
2.Если обе части аоо-либо уравнения системы, умно-
женные на неоторое (отличное от нуля) число, вычесть из со-
ответствующих частей друоо уравнения и составить систему,
в оторой одно из упомянутых уравнений заменено уравнени-

62 Г л а в а 3. Системы уравнений
ем, полученным в результате вычитания, а остальные уравне-
ния оставлены без изменений, то полученная система будет
эвивалентна исходной.
§ 13. Системы линейных уравнений
Метод Гасса. При нахождении решений системы m линей-
ных уравнений с n неизвестными удобно использовать метод
Гасса, состоящий в том, что систему приводят треуольно-
му или трапециедальному виду.
П р и м е р 1. Решить систему
(*)
Р е ш е н и е. Умножим обе части первоо уравнения систе-
мы (*) на (–3) и сложим со вторым уравнением: тода получим
уравнение –5y – 8z = –18, или
5y + 8z = 18.
Далее, умножив обе части первоо уравнения системы (*) на
(–2) и сложив с третьим ее уравнением, получаем уравнение
–3y –4z = –10, или
3y + 4z = 10.
Следовательно, данную систему можно записать в виде эвива-
лентной системы, в оторой второе и третье уравнения не со-
держат неизвестноо x:
(**)
Умножив обе части второо уравнения системы (**) на 3, а
третьео — на (–5) и сложив эти уравнения, придем урав-
нению 4z = 4. Таим образом, система (**) эвивалентна сле-
дующей:
(***)
Ита, исходная система приведена треуольному виду. Под-
ставляя z = 1 во второе уравнение системы (***), находим y = 2.
0x + 2y + 3z = 8,
3x + 0y + 0z = 6,
2x + 0y + 2z = 6.
x + 2y + 3z = 18,
x + 5y + 8z = 18,
x + 3y + 4z = 10.
x + 2y + 3z = 18,
x + 5y + 8z = 18,
x + 2y + 8z = 11.
§ 13. Системы линейных уравнений 63
Подставляя значения z = 1 и y = 2 в первое уравнение той же
системы, находим x = 1.
Ответ. x = 1, y = 2, z = 1.
Решите систему линейных уравнений методом Гаусса:
1. 2.
3. 4.
5. 6.
Решение и исследование систем двх линейных равнений
с двмя неизвестными. Рассмотрим систему двух линейных
уравнений с двумя неизвестными
(1)
при условии, что хотя бы один из оэффициентов отличен от
нуля. Обозначим через ∆, и соответственно следующие
определители:
∆ = = a
11
a
22
– a
12
a
21
,
∆
x
= = b
1
a
22
– b
2
a
12
,
∆
y
= = a
11
b
2
– a
21
b
1
.
Тода справедливо следующее утверждение
.
Если ∆ − 0, то система (1) имеет единственное решение
x = , y = .
2x + 2y + 2z = 7,
2x + 2y + 2z = 8,
2x + 2y + 2z = 9.
3x – 4y + 5z = 18,
2x + 4y – 3z = 26,
0x – 6y + 8z = 00.
10x – y – 19z = 19,
18x – y – 12z = 10,
10x – y – 12z = 10.
0x + 2y + 0z + 7 = 0,
2x + 2y – 0z – 1 = 0,
3x – 2y + 2z – 2 = 0.
– + = 1,
– + = 1,
– + = 1.
x
a
3
------
y
a
2
------
z
a
---
x
b
3
-----
y
b
2
-----
z
b
-- -
x
c
3
-----
y
c
2
-----
z
c
-- -
x + a
2
y + b
2
z = 0,
x + ay + bz = 0,
x + y + z = 1.
a
11
x + a
12
y = b
1
,
a
21
x + a
22
y = b
2
∆
x
∆
y
a
11
a
21
a
12
a
22
b
1
b
2
a
12
a
22
a
11
a
21
b
1
b
2
∆
x
∆
------
∆
y
∆
------

62 Г л а в а 3. Системы уравнений
ем, полученным в результате вычитания, а остальные уравне-
ния оставлены без изменений, то полученная система будет
эвивалентна исходной.
§ 13. Системы линейных уравнений
Метод Гасса. При нахождении решений системы m линей-
ных уравнений с n неизвестными удобно использовать метод
Гасса, состоящий в том, что систему приводят треуольно-
му или трапециедальному виду.
П р и м е р 1. Решить систему
(*)
Р е ш е н и е. Умножим обе части первоо уравнения систе-
мы (*) на (–3) и сложим со вторым уравнением: тода получим
уравнение –5y – 8z = –18, или
5y + 8z = 18.
Далее, умножив обе части первоо уравнения системы (*) на
(–2) и сложив с третьим ее уравнением, получаем уравнение
–3y –4z = –10, или
3y + 4z = 10.
Следовательно, данную систему можно записать в виде эвива-
лентной системы, в оторой второе и третье уравнения не со-
держат неизвестноо x:
(**)
Умножив обе части второо уравнения системы (**) на 3, а
третьео — на (–5) и сложив эти уравнения, придем урав-
нению 4z = 4. Таим образом, система (**) эвивалентна сле-
дующей:
(***)
Ита, исходная система приведена треуольному виду. Под-
ставляя z = 1 во второе уравнение системы (***), находим y = 2.
0x + 2y + 3z = 8,
3x + 0y + 0z = 6,
2x + 0y + 2z = 6.
x + 2y + 3z = 18,
x + 5y + 8z = 18,
x + 3y + 4z = 10.
x + 2y + 3z = 18,
x + 5y + 8z = 18,
x + 2y + 8z = 11.
§ 13. Системы линейных уравнений 63
Подставляя значения z = 1 и y = 2 в первое уравнение той же
системы, находим x = 1.
Ответ. x = 1, y = 2, z = 1.
Решите систему линейных уравнений методом Гаусса:
1. 2.
3. 4.
5. 6.
Решение и исследование систем двх линейных равнений
с двмя неизвестными. Рассмотрим систему двух линейных
уравнений с двумя неизвестными
(1)
при условии, что хотя бы один из оэффициентов отличен от
нуля. Обозначим через ∆, и соответственно следующие
определители:
∆ = = a
11
a
22
– a
12
a
21
,
∆
x
= = b
1
a
22
– b
2
a
12
,
∆
y
= = a
11
b
2
– a
21
b
1
.
Тода справедливо следующее утверждение
.
Если ∆ − 0, то система (1) имеет единственное решение
x = , y = .
2x + 2y + 2z = 7,
2x + 2y + 2z = 8,
2x + 2y + 2z = 9.
3x – 4y + 5z = 18,
2x + 4y – 3z = 26,
0x – 6y + 8z = 00.
10x – y – 19z = 19,
18x – y – 12z = 10,
10x – y – 12z = 10.
0x + 2y + 0z + 7 = 0,
2x + 2y – 0z – 1 = 0,
3x – 2y + 2z – 2 = 0.
– + = 1,
– + = 1,
– + = 1.
x
a
3
------
y
a
2
------
z
a
---
x
b
3
-----
y
b
2
-----
z
b
-- -
x
c
3
-----
y
c
2
-----
z
c
-- -
x + a
2
y + b
2
z = 0,
x + ay + bz = 0,
x + y + z = 1.
a
11
x + a
12
y = b
1
,
a
21
x + a
22
y = b
2
∆
x
∆
y
a
11
a
21
a
12
a
22
b
1
b
2
a
12
a
22
a
11
a
21
b
1
b
2
∆
x
∆
------
∆
y
∆
------

64 Г л а в а 3. Системы уравнений
Если ∆ = 0, то:
1) в случае, ода хотя бы один из определителей или
не равен нулю, система (1) является несовместной (т. е.
не имеет решений);
2) в случае, ода = = 0, система (1) является сов-
местной и неопределенной (т.е. имеет бесонечно мноо ре-
шений).
Каждое из уравнений системы (1) задает линейное соответ-
ствие между переменными x и y. Всяое линейное соответствие
между переменными x и y определяет в прямоуольной системе
оординат неоторую прямую. Если система имеет единственное
решение, то прямые, задаваемые ее уравнениями, пересеаются.
Если система имеет бесчисленное множество решений, то прямые
совпадают; если система несовместна, то прямые параллельны.
П р и м е р 2. Решить и исследовать систему
Р е ш е н и е. Вычислим определители ∆, и :
∆ = = a
2
– 1,
= = 2a – 2a = 0,
= = 2a
2
– 2.
1. Пусть ∆ = a
2
– 1 − 0, т. е. a − ä1. В этом случае система
имеет единственное решение:
x = = = 0, y = = = 2.
2. Пусть ∆ = a
2
– 1 = 0, т. е. a = ä1. В этом случае ∆ = =
= = 0, т. е. система совместная и неопределенная.
При a = 1 система примет вид
и ее решениями являются все пары чисел (x; y), связанные ра-
венством x + y = 2.
∆
x
∆
y
∆
x
∆
y
ax + ay = 2,
ax + ay = 2a.
∆
x
∆
y
a
1
1
a
∆
x
2
2a
1
a
∆
y
a
1
2
2a
∆
x
∆
------
0
a
2
1–
----------------
∆
y
∆
------
2a
2
2–
a
2
1–
--------------------
∆
x
∆
y
x + y = 2,
x + y = 2,
§ 13. Системы линейных уравнений 65
При a = –1 имеем
^
и ее решениями являются все пары чисел (x; y), связанные ра-
венством x – y = –2.
Ответ.При a − ä1 система имеет единственное решение
x = 0, y = 2;
при a = 1 решения системы — все пары чисел (x; y) таих,
что x + y = 2;
при a = –1 решения системы — все пары чисел (x; y) таих,
что x – y = –2.
Исследуйте систему уравнений:
7.
8.
9.
10.
11.
12.
13. Найдите таие значения параметров m и p, при оторых
система
была бы неопределенной.
14. Совместны ли уравнения
x + ay = b + c,
x + by = c + a,
x + cy = a + b,
де a
2
+ b
2
+ c
2
= 1 и a, b, c— действительные числа?
–x + y = 2,
–x – y = –2
x – y = –2,
x – y = –2,
x + ay – 1 = 0,
ax – 3ay – (2a + 3) = 0.
3x + ay = 5a
2
,
3x – ay = a
2
.
(a + 5)x + (2a + 3)y – (3a + 2) = 0,
(3a + 10)x + (5a + 6)y – (2a + 4) = 0.
a(a – 1)x + (a + 1)ay = a
3
+ 2,
(a
2
– 1)x + (a
3
+ 1)y = a
4
– 1.
ax – y = b,
bx + y = a.
(a
2
+ b
2
)x + (a
2
– b
2
)y = a
2
,
(a + b)x + (a – b)y = a.
2
(3m – 5p + b)x + (8m – 3p – a)y = 1,
(2m – 3p + b)x + (4m – p)y = 2,

64 Г л а в а 3. Системы уравнений
Если ∆ = 0, то:
1) в случае, ода хотя бы один из определителей или
не равен нулю, система (1) является несовместной (т. е.
не имеет решений);
2) в случае, ода = = 0, система (1) является сов-
местной и неопределенной (т.е. имеет бесонечно мноо ре-
шений).
Каждое из уравнений системы (1) задает линейное соответ-
ствие между переменными x и y. Всяое линейное соответствие
между переменными x и y определяет в прямоуольной системе
оординат неоторую прямую. Если система имеет единственное
решение, то прямые, задаваемые ее уравнениями, пересеаются.
Если система имеет бесчисленное множество решений, то прямые
совпадают; если система несовместна, то прямые параллельны.
П р и м е р 2. Решить и исследовать систему
Р е ш е н и е. Вычислим определители ∆, и :
∆ = = a
2
– 1,
= = 2a – 2a = 0,
= = 2a
2
– 2.
1. Пусть ∆ = a
2
– 1 − 0, т. е. a − ä1. В этом случае система
имеет единственное решение:
x = = = 0, y = = = 2.
2. Пусть ∆ = a
2
– 1 = 0, т. е. a = ä1. В этом случае ∆ = =
= = 0, т. е. система совместная и неопределенная.
При a = 1 система примет вид
и ее решениями являются все пары чисел (x; y), связанные ра-
венством x + y = 2.
∆
x
∆
y
∆
x
∆
y
ax + ay = 2,
ax + ay = 2a.
∆
x
∆
y
a
1
1
a
∆
x
2
2a
1
a
∆
y
a
1
2
2a
∆
x
∆
------
0
a
2
1–
----------------
∆
y
∆
------
2a
2
2–
a
2
1–
--------------------
∆
x
∆
y
x + y = 2,
x + y = 2,
§ 13. Системы линейных уравнений 65
При a = –1 имеем
^
и ее решениями являются все пары чисел (x; y), связанные ра-
венством x – y = –2.
Ответ.При a − ä1 система имеет единственное решение
x = 0, y = 2;
при a = 1 решения системы — все пары чисел (x; y) таих,
что x + y = 2;
при a = –1 решения системы — все пары чисел (x; y) таих,
что x – y = –2.
Исследуйте систему уравнений:
7.
8.
9.
10.
11.
12.
13. Найдите таие значения параметров m и p, при оторых
система
была бы неопределенной.
14. Совместны ли уравнения
x + ay = b + c,
x + by = c + a,
x + cy = a + b,
де a
2
+ b
2
+ c
2
= 1 и a, b, c— действительные числа?
–x + y = 2,
–x – y = –2
x – y = –2,
x – y = –2,
x + ay – 1 = 0,
ax – 3ay – (2a + 3) = 0.
3x + ay = 5a
2
,
3x – ay = a
2
.
(a + 5)x + (2a + 3)y – (3a + 2) = 0,
(3a + 10)x + (5a + 6)y – (2a + 4) = 0.
a(a – 1)x + (a + 1)ay = a
3
+ 2,
(a
2
– 1)x + (a
3
+ 1)y = a
4
– 1.
ax – y = b,
bx + y = a.
(a
2
+ b
2
)x + (a
2
– b
2
)y = a
2
,
(a + b)x + (a – b)y = a.
2
(3m – 5p + b)x + (8m – 3p – a)y = 1,
(2m – 3p + b)x + (4m – p)y = 2,

66 Г л а в а 3. Системы уравнений
15. Числа a и b таовы, что система
имеет единственное решение x = 1, y = 1. Найдите числа a и b.
16. При аих значениях a и b система
имеет бесонечно мноо решений?
17. При аих значениях a система
не имеет решений?
18. Числа a, b и c таовы, что система
имеет бесонечно мноо решений, причем x = 1, y = 3 — одно
из этих решений. Найдите a, b и c.
19. При аих значениях параметра a система уравнений
не имеет решений?
20. При аих значениях параметра a система
имеет бесонечно мноо решений?
§ 14. Системы нелинейных уравнений
Системы, содержащие линейное равнение. Если одно из
уравнений системы двух уравнений с двумя неизвестными ли-
нейное, в друое — нелинейное, то таую систему решают сле-
дующим способом. Из линейноо уравнения выражают одно
a
2
x – ay = 1 – a,
bx + (3 – 2b)y = 3 + a,
a
2
x – by = a
2
– b,
bx – b
2
y = 2 + 4b
a
2
x + (2 – a)y = 4 + a
3
,
ax + (2a – 1)y = a
5
– 2
ax – by = 2a – b,
(c + 1)x + cy = 10 – a + 3b
ax – 4y = a + 1,
2x + (a + 6)y = a + 3,
2x + ay = a + 2,
(a + 1)x + 2ay = 2a + 4
§ 14. Системы нелинейных уравнений 67
неизвестное через друое и подставляют в оставшееся уравне-
ние, оторое после этоо превращается в алебраичесое урав-
нение с одним неизвестным.
П р и м е р 1. Решить систему
Р е ш е н и е. Из второо уравнения следует, что y = –x – 8.
Подставив это выражение вместо y в первое уравнение систе-
мы, получим
x
2
+ (x + 8)
2
+ 6x – 2(x + 8) = 0,
или
x
2
+ 10x + 24 = 0,
отуда x
1
= –4, x
2
= –6. Соответствующие значения y найдем
из уравнения y = –x – 8. Имеем y
1
= –4, y
2
= –2. Ита, система
имеет два решения: (–4; –4) и (–6; –2).
Ответ. (–4; –4), (–6; –2).
Решите систему уравнений:
1.
2.
3.
4.
5.
6.
Системы, содержащие однородное равнение. В тех случаях,
ода одно из двух уравнений нелинейной системы однород-
ное, можно с помощью этоо уравнения линейно выразить одно
неизвестное системы через друое.
x
2
+ y
2
+ 6x + 2y = 0,
x + y + 8 = 0.
(x – y)(x
2
– y
2
) = 45,
x + y = 5.
(x + 0,2)
2
+ (y + 0,3)
2
= 1,
x + y = 0,9.
+ = ,
x + y = 5.
x
y
---
y
x
---
13
6
------
(x + y)
4
+ 4(x + y)
2
– 117 = 0,
x – y = 25.
x
2
+ y
2
= 2(xy + 2),
x + y = 6.
x
2
+ y
2
+ 10x – 10y = 2xy – 21,
x + y = 5.

66 Г л а в а 3. Системы уравнений
15. Числа a и b таовы, что система
имеет единственное решение x = 1, y = 1. Найдите числа a и b.
16. При аих значениях a и b система
имеет бесонечно мноо решений?
17. При аих значениях a система
не имеет решений?
18. Числа a, b и c таовы, что система
имеет бесонечно мноо решений, причем x = 1, y = 3 — одно
из этих решений. Найдите a, b и c.
19. При аих значениях параметра a система уравнений
не имеет решений?
20. При аих значениях параметра a система
имеет бесонечно мноо решений?
§ 14. Системы нелинейных уравнений
Системы, содержащие линейное равнение. Если одно из
уравнений системы двух уравнений с двумя неизвестными ли-
нейное, в друое — нелинейное, то таую систему решают сле-
дующим способом. Из линейноо уравнения выражают одно
a
2
x – ay = 1 – a,
bx + (3 – 2b)y = 3 + a,
a
2
x – by = a
2
– b,
bx – b
2
y = 2 + 4b
a
2
x + (2 – a)y = 4 + a
3
,
ax + (2a – 1)y = a
5
– 2
ax – by = 2a – b,
(c + 1)x + cy = 10 – a + 3b
ax – 4y = a + 1,
2x + (a + 6)y = a + 3,
2x + ay = a + 2,
(a + 1)x + 2ay = 2a + 4
§ 14. Системы нелинейных уравнений 67
неизвестное через друое и подставляют в оставшееся уравне-
ние, оторое после этоо превращается в алебраичесое урав-
нение с одним неизвестным.
П р и м е р 1. Решить систему
Р е ш е н и е. Из второо уравнения следует, что y = –x – 8.
Подставив это выражение вместо y в первое уравнение систе-
мы, получим
x
2
+ (x + 8)
2
+ 6x – 2(x + 8) = 0,
или
x
2
+ 10x + 24 = 0,
отуда x
1
= –4, x
2
= –6. Соответствующие значения y найдем
из уравнения y = –x – 8. Имеем y
1
= –4, y
2
= –2. Ита, система
имеет два решения: (–4; –4) и (–6; –2).
Ответ. (–4; –4), (–6; –2).
Решите систему уравнений:
1.
2.
3.
4.
5.
6.
Системы, содержащие однородное равнение. В тех случаях,
ода одно из двух уравнений нелинейной системы однород-
ное, можно с помощью этоо уравнения линейно выразить одно
неизвестное системы через друое.
x
2
+ y
2
+ 6x + 2y = 0,
x + y + 8 = 0.
(x – y)(x
2
– y
2
) = 45,
x + y = 5.
(x + 0,2)
2
+ (y + 0,3)
2
= 1,
x + y = 0,9.
+ = ,
x + y = 5.
x
y
---
y
x
---
13
6
------
(x + y)
4
+ 4(x + y)
2
– 117 = 0,
x – y = 25.
x
2
+ y
2
= 2(xy + 2),
x + y = 6.
x
2
+ y
2
+ 10x – 10y = 2xy – 21,
x + y = 5.
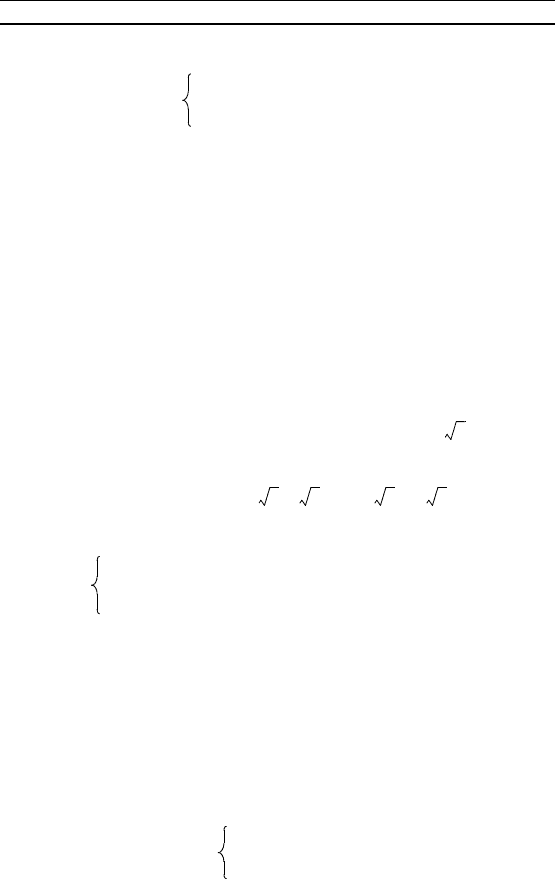
68 Г л а в а 3. Системы уравнений
П р и м е р 2. Решить систему уравнений
(*)
Р е ш е н и е. Первое уравнение системы (*) — однородное.
Разделив обе ео части на y
2
, получим относительно неизвест-
ноо t = вадратное уравнение
t
2
– 5t + 6 = 0,
орнями отороо являются t
1
= 3, t
2
= 2. Таим образом, име-
ем следующие линейные зависимости между неизвестными,
входящими в исходную систему (*):
x = 3y, x = 2y. (**)
Подставляя последовательно x = 3y и x = 2y во второе урав-
нение данной системы, приходим вадратным уравнениям
y
2
= 1 и y
2
= 2, имеющим орни y
1, 2
= ä1, y
3, 4
= ä . Соответ-
ствующие значения x
1
, x
2
, x
3
, x
4
находим из равенств (**).
Ответ. (3; 1), (–3; –1), (2 ; ), (–2 ; – ).
Систему вида
d
1
− 0, d
2
− 0,
сводят системе, содержащей однородное уравнение, следую-
щим образом: умножают обе части первоо уравнения на d
2
,
обе части второо — на (–d
1
) и сладывают оба преобразован-
ных уравнения. В результате получают однородное уравнение.
Далее исходную систему заменяют эвивалентной системой,
содержащей полученное однородное уравнение и одно из урав-
нений исходной системы.
П р и м е р 3. Решить систему уравнений
Р е ш е н и е. Умножив обе части первоо уравнения на 2,
обе части второо — на (–1) и сложив полученные уравнения,
приходим однородному уравнению
x
2
– 2y
2
– xy = 0.
x
2
– 5xy + 6y
2
= 0,
x
2
+ y
2
= 10.
x
y
---
2
2 2 2 2
a
1
x
2
+ b
1
y
2
+ c
1
xy = d
1
,
a
2
x
2
+ b
2
y
2
+ c
2
xy = d
2
,
x
2
– y
2
= 1,
x
2
+ xy = 2.
§ 14. Системы нелинейных уравнений 69
Разделив обе части этоо уравнения на y
2
, получим относитель-
но z = вадратное уравнение
z
2
– z – 2 = 0,
орни отороо z
1
= –1, z
2
= 2.
Таим образом, исходная система эвивалентна двум сис-
темам
и
первая из оторых несовместна, а решением второй являются
две пары чисел: ; и – ; – .
Ответ.; , –; –.
Решите систему уравнений:
7. 8.
9. 10.
Симметричесие системы. Систему уравнений с n неизвест-
ными x
1
, x
2
, ..., x
n
называют симметричесой, если она не ме-
няется при перестанове неизвестных. Если система содержит
два неизвестных (x и y), то часто решение таой системы мож-
но найти с помощью введения новых неизвестных u = x + y,
v = xy. При этом удобно использовать следующие равенства:
x
2
+ y
2
= (x + y)
2
– 2xy = u
2
– 2v,
x
3
+ y
3
= (x + y)
3
– 3xy(x + y) = u
3
– 3uv,
x
4
+ y
4
= (x
2
+ y
2
)
2
– 2x
2
y
2
=
= ((x + y)
2
– 2xy)
2
– 2x
2
y
2
= (u
2
– 2v)
2
– 2v
2
,
позволяющие выразить омбинации неизвестных x
2
+ y
2
, x
3
+ y
3
,
x
4
+ y
4
через неизвестные u и v.
x
y
---
x
2
– y
2
= 1,
= –1
x
y
---
x
2
– y
2
= 1,
= 2,
x
y
---
23
3
-----------
3
3
-------
23
3
-----------
3
3
-------
23
3
-----------
3
3
-------
23
3
-----------
3
3
-------
x
2
y
3
+ x
3
y
2
= 12,
x
2
y
3
– x
3
y
2
= 4.
x
3
+ y
3
= 65,
x
2
y + xy
2
= 20.
x
4
– y
4
= 15,
x
3
y – xy
3
= 6.
x
2
+ 2y
2
= 17,
x
2
– 2xy = –3.
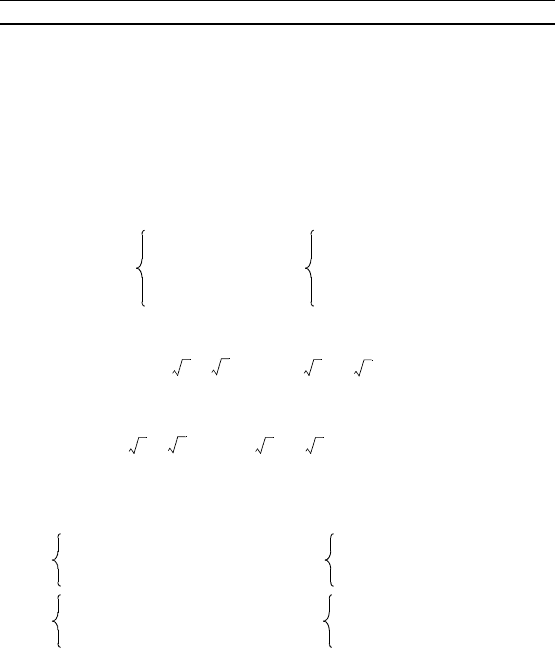
68 Г л а в а 3. Системы уравнений
П р и м е р 2. Решить систему уравнений
(*)
Р е ш е н и е. Первое уравнение системы (*) — однородное.
Разделив обе ео части на y
2
, получим относительно неизвест-
ноо t = вадратное уравнение
t
2
– 5t + 6 = 0,
орнями отороо являются t
1
= 3, t
2
= 2. Таим образом, име-
ем следующие линейные зависимости между неизвестными,
входящими в исходную систему (*):
x = 3y, x = 2y. (**)
Подставляя последовательно x = 3y и x = 2y во второе урав-
нение данной системы, приходим вадратным уравнениям
y
2
= 1 и y
2
= 2, имеющим орни y
1, 2
= ä1, y
3, 4
= ä . Соответ-
ствующие значения x
1
, x
2
, x
3
, x
4
находим из равенств (**).
Ответ. (3; 1), (–3; –1), (2 ; ), (–2 ; – ).
Систему вида
d
1
− 0, d
2
− 0,
сводят системе, содержащей однородное уравнение, следую-
щим образом: умножают обе части первоо уравнения на d
2
,
обе части второо — на (–d
1
) и сладывают оба преобразован-
ных уравнения. В результате получают однородное уравнение.
Далее исходную систему заменяют эвивалентной системой,
содержащей полученное однородное уравнение и одно из урав-
нений исходной системы.
П р и м е р 3. Решить систему уравнений
Р е ш е н и е. Умножив обе части первоо уравнения на 2,
обе части второо — на (–1) и сложив полученные уравнения,
приходим однородному уравнению
x
2
– 2y
2
– xy = 0.
x
2
– 5xy + 6y
2
= 0,
x
2
+ y
2
= 10.
x
y
---
2
2 2 2 2
a
1
x
2
+ b
1
y
2
+ c
1
xy = d
1
,
a
2
x
2
+ b
2
y
2
+ c
2
xy = d
2
,
x
2
– y
2
= 1,
x
2
+ xy = 2.
§ 14. Системы нелинейных уравнений 69
Разделив обе части этоо уравнения на y
2
, получим относитель-
но z = вадратное уравнение
z
2
– z – 2 = 0,
орни отороо z
1
= –1, z
2
= 2.
Таим образом, исходная система эвивалентна двум сис-
темам
и
первая из оторых несовместна, а решением второй являются
две пары чисел: ; и – ; – .
Ответ.; , –; –.
Решите систему уравнений:
7. 8.
9. 10.
Симметричесие системы. Систему уравнений с n неизвест-
ными x
1
, x
2
, ..., x
n
называют симметричесой, если она не ме-
няется при перестанове неизвестных. Если система содержит
два неизвестных (x и y), то часто решение таой системы мож-
но найти с помощью введения новых неизвестных u = x + y,
v = xy. При этом удобно использовать следующие равенства:
x
2
+ y
2
= (x + y)
2
– 2xy = u
2
– 2v,
x
3
+ y
3
= (x + y)
3
– 3xy(x + y) = u
3
– 3uv,
x
4
+ y
4
= (x
2
+ y
2
)
2
– 2x
2
y
2
=
= ((x + y)
2
– 2xy)
2
– 2x
2
y
2
= (u
2
– 2v)
2
– 2v
2
,
позволяющие выразить омбинации неизвестных x
2
+ y
2
, x
3
+ y
3
,
x
4
+ y
4
через неизвестные u и v.
x
y
---
x
2
– y
2
= 1,
= –1
x
y
---
x
2
– y
2
= 1,
= 2,
x
y
---
23
3
-----------
3
3
-------
23
3
-----------
3
3
-------
23
3
-----------
3
3
-------
23
3
-----------
3
3
-------
x
2
y
3
+ x
3
y
2
= 12,
x
2
y
3
– x
3
y
2
= 4.
x
3
+ y
3
= 65,
x
2
y + xy
2
= 20.
x
4
– y
4
= 15,
x
3
y – xy
3
= 6.
x
2
+ 2y
2
= 17,
x
2
– 2xy = –3.
