Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


626 Ответы, указания, решения
содержащео 10 элементов; порядо элементов в выборе несу-
ществен. 11. 40 · 39 · омиссий.
Председатель и сере-
тарь образуют выбору без повторений, состоящую из двух
элементов исходноо множества, содержащео 40 элементов;
5 членов омиссии образуют выбору без повторений неоторо-
о состава из исходноо множества, содержащео 38 членов.
12. · буетов. 13. · способами. 14. · ·
бриад. 15. а) 49 · различных арточе; б) · различ-
ных арточе; в) · различных арточе. 16. 120 оруж-
ностей. 17. В – случаях.
Исомое оличество равно
разности общео числа способов извлечь 10 арт из 52 и чис-
ла способов извлечь 10 арт из 48 та, чтобы среди 10 арт
не было туза. 18. 4· способами. 19. · способами.
20. 1225 чисел.
Учтите, что цифровая запись числа не может
начинаться с нуля. 21. 750 чисел.
§ 83. Перестановки и сочетания
с заданным числом повторений
1. 2520 омбинаций. 2. 165 наборов. Выбора объема 8
с заданным числом повторений производится из четырех рупп
однородных элементов. 3. = способами.
Выбора объе-
ма 7 с заданным числом повторений производится из 10 рупп
одинаовых элементов. 4. способов.
Найдите число
различных выборо состава (13, 13, 13, 13). 5. способов.
Шесть различных рупп однородных элементов должны со-
ставить выбору с заданным числом повторений, содержащую
12 элементов и имеющую состав (2, 2, 2, 2, 2, 2). 6. спо-
собами.
Рассмотрите выбору с заданным числом повторе-
ний, имеющую состав (m + 1, n), де m + 1 — оличество про-
межутов между m белыми шарами, а n— оличество черных
шаров. Число различных расстаново равно числу всевозмож-
ных выборо состава (m + 1, n). 7. испытаний.
Найди-
C
38
5
C
8
3
C
10
2
C
32
4
C
4
2
C
5
1
C
15
2
C
10
3
C
6
5
C
43
2
C
6
4
C
43
3
C
6
3
C
52
10
C
48
10
C
44
4
A
10
4
A
6
4
C
10
7
C
16
7
52!
13!()
4
----------------
12!
2
6
-------- -
C
m 1+
n
100!
48!52!
------------------
Г л а в а 15. Комбинаторика. Элементы теории вероятностей 627
те число различных выборо состава (n
1
, n
2
), де n
1
= 52—
число успехов, а n
1
+ n
2
= 100. 8. 2 · (6!)
2
способами. Число
перестаново левых мест ряда умножьте на число перестаново
правых мест. Учтите возможность смены левых мест на правые.
9.
Воспользуйтесь неравенством · m ( )
2
, до-
азательство отороо можно провести непосредственно.
§ 84. Бином Ньютона
1. 1024.
Разложите выражение (1 + 1)
10
по формуле бино-
ма. 2. k = 4. 3. T
2
= x
6,5
= 153x
6,5
. Воспользуйтесь тем,
что наибольший оэффициент имеет средний член разложения.
4. 28x
2
a
–4
. 5. См. уазание упр. 1. 6. –1375.
7. .
Рассмотрим отношение . Та а
T
k + 1
= , T
k
= ,
то
= = .
Если > 1, то T
k + 1
> T
k
, а если < 1, то
T
k + 1
< T
k
. Значит, при k < 50 члены T
k
возрастают, а при
k > 50 — убывают. Следовательно, наибольшим членом являет-
ся T
50
= .
8. Десятый член. 9. T
3
= x
11
. Степень бинома можно
найти, используя уазание упр. 1. 10.
Воспользуйтесь бино-
миальным разложением для . 11. –264a
3
b
7
. Используй-
те результат упр. 10. 12. 314 925 · 10
5
. 13. x = 2. 14. < x < .
См. решение упр. 7. 15. x = 0,5. Используя условие, пред-
ставьте 50-й член разложения а фунцию арумента x и най-
дите наибольшее значение этой фунции на промежуте [0; 1].
16. x = . 17. · 3
2
· 2
2
. 18. 26.
C
2nk+
n
C
2nk–
n
C
2n
n
C
18
2
C
100
50
1
2
---
100
T
k 1+
T
k
-------------- -
C
100
k 1+
1
2
---
100
C
100
k
1
2
---
100
T
k 1+
T
k
-------------- -
100! k! 100 k–1+()!
k 1+()!100 k–()! 100!⋅
-----------------------------------------------------------------
100 k–1+
k 1+
------------------------------ -
100 k–1+
k 1+
------------------------------ -
100 k–1+
k 1+
------------------------------ -
C
100
50
1
2
---
100
C
10
3
(1 1)
n
–
5
8
---
20
21
------
nk–
n
-------------
C
24
14

626 Ответы, указания, решения
содержащео 10 элементов; порядо элементов в выборе несу-
ществен. 11. 40 · 39 · омиссий.
Председатель и сере-
тарь образуют выбору без повторений, состоящую из двух
элементов исходноо множества, содержащео 40 элементов;
5 членов омиссии образуют выбору без повторений неоторо-
о состава из исходноо множества, содержащео 38 членов.
12. · буетов. 13. · способами. 14. · ·
бриад. 15. а) 49 · различных арточе; б) · различ-
ных арточе; в) · различных арточе. 16. 120 оруж-
ностей. 17. В – случаях.
Исомое оличество равно
разности общео числа способов извлечь 10 арт из 52 и чис-
ла способов извлечь 10 арт из 48 та, чтобы среди 10 арт
не было туза. 18. 4· способами. 19. · способами.
20. 1225 чисел.
Учтите, что цифровая запись числа не может
начинаться с нуля. 21. 750 чисел.
§ 83. Перестановки и сочетания
с заданным числом повторений
1. 2520 омбинаций. 2. 165 наборов. Выбора объема 8
с заданным числом повторений производится из четырех рупп
однородных элементов. 3. = способами.
Выбора объе-
ма 7 с заданным числом повторений производится из 10 рупп
одинаовых элементов. 4. способов.
Найдите число
различных выборо состава (13, 13, 13, 13). 5. способов.
Шесть различных рупп однородных элементов должны со-
ставить выбору с заданным числом повторений, содержащую
12 элементов и имеющую состав (2, 2, 2, 2, 2, 2). 6. спо-
собами.
Рассмотрите выбору с заданным числом повторе-
ний, имеющую состав (m + 1, n), де m + 1 — оличество про-
межутов между m белыми шарами, а n— оличество черных
шаров. Число различных расстаново равно числу всевозмож-
ных выборо состава (m + 1, n). 7. испытаний.
Найди-
C
38
5
C
8
3
C
10
2
C
32
4
C
4
2
C
5
1
C
15
2
C
10
3
C
6
5
C
43
2
C
6
4
C
43
3
C
6
3
C
52
10
C
48
10
C
44
4
A
10
4
A
6
4
C
10
7
C
16
7
52!
13!()
4
----------------
12!
2
6
-------- -
C
m 1+
n
100!
48!52!
------------------
Г л а в а 15. Комбинаторика. Элементы теории вероятностей 627
те число различных выборо состава (n
1
, n
2
), де n
1
= 52—
число успехов, а n
1
+ n
2
= 100. 8. 2 · (6!)
2
способами. Число
перестаново левых мест ряда умножьте на число перестаново
правых мест. Учтите возможность смены левых мест на правые.
9.
Воспользуйтесь неравенством · m ( )
2
, до-
азательство отороо можно провести непосредственно.
§ 84. Бином Ньютона
1. 1024.
Разложите выражение (1 + 1)
10
по формуле бино-
ма. 2. k = 4. 3. T
2
= x
6,5
= 153x
6,5
. Воспользуйтесь тем,
что наибольший оэффициент имеет средний член разложения.
4. 28x
2
a
–4
. 5. См. уазание упр. 1. 6. –1375.
7. .
Рассмотрим отношение . Та а
T
k + 1
= , T
k
= ,
то
= = .
Если > 1, то T
k + 1
> T
k
, а если < 1, то
T
k + 1
< T
k
. Значит, при k < 50 члены T
k
возрастают, а при
k > 50 — убывают. Следовательно, наибольшим членом являет-
ся T
50
= .
8. Десятый член. 9. T
3
= x
11
. Степень бинома можно
найти, используя уазание упр. 1. 10.
Воспользуйтесь бино-
миальным разложением для . 11. –264a
3
b
7
. Используй-
те результат упр. 10. 12. 314 925 · 10
5
. 13. x = 2. 14. < x < .
См. решение упр. 7. 15. x = 0,5. Используя условие, пред-
ставьте 50-й член разложения а фунцию арумента x и най-
дите наибольшее значение этой фунции на промежуте [0; 1].
16. x = . 17. · 3
2
· 2
2
. 18. 26.
C
2nk+
n
C
2nk–
n
C
2n
n
C
18
2
C
100
50
1
2
---
100
T
k 1+
T
k
-------------- -
C
100
k 1+
1
2
---
100
C
100
k
1
2
---
100
T
k 1+
T
k
-------------- -
100! k! 100 k–1+()!
k 1+()!100 k–()! 100!⋅
-----------------------------------------------------------------
100 k–1+
k 1+
------------------------------ -
100 k–1+
k 1+
------------------------------ -
100 k–1+
k 1+
------------------------------ -
C
100
50
1
2
---
100
C
10
3
(1 1)
n
–
5
8
---
20
21
------
nk–
n
-------------
C
24
14

628 Ответы, указания, решения
19. Первое, пятое и девятое слааемые разложения. Та
а оэффициенты 1, , образуют арифметичесую
прорессию, то можно составить уравнение
+ 1 = n,
имеющее орни n = 8 и n = 1; n = 1 — посторонний орень.
При n = 8 общий член разложения запишется в виде
T
k
= = 2
k – 8
.
Этот член является рациональным, если k + 8 ратно 4, де 0 m
m k m 8. Уазанное условие выполняется при k = 0, 4, 8. Следо-
вательно, рациональными являются члены T
0
, T
4
, T
8
.
20.
Используйте биномиальное разложение для .
23.
Рассмотрите биномиальное разложение для .
25. Найдите приращения первообразной фунции (1 + x)
n
на
промежуте [0; 1] непосредственно и записав выражение для
по формуле бинома Ньютона. 26.
Найдите производ-
ную фунции в точе x = 1. 27.
Сравните прираще-
ния первообразной фунции на промежуте [0; 1],
найденные непосредственно и с помощью предварительноо раз-
ложения по формуле бинома Ньютона. 28. (n + 1)! – 1.
К исомому выражению прибавьте и отнимите P
1
+ P
2
+ ...
... + P
n
. 29. Используйте тождество + = .
§ 85. Вычисление вероятностей
с помощью формул комбинаторики
1. . 2. . 3. . Количество двузначных чисел равно
90. Количество двузначных чисел, делящихся на 3, найдите из
уравнения 99 = 12 + 3(n – 1). 4. 0,4. 5. .
n
2
---
nn 1–()
8
-----------------------
nn 1–()
8
-----------------------
C
8
k
x
k
2
---
1
2
---
8 k–
x
8 k–
4
---------- ---
x
k 8+
4
---------- --- -
C
8
k
(1 1)
n
–
(10 1)
2n
–
(1 x)
n
+
(x 1)
n
–
(x 1)
n
–
(x 1)
n
–
C
n
k
C
n
k 1–
C
n 1+
k
12
365
----------
5
12
------
1
3
---
3
13
------
Г л а в а 15. Комбинаторика. Элементы теории вероятностей 629
6. P(A) = , P(B) = . Пространство элементарных собы-
тий состоит из таих выборо с повторениями, оторые содер-
жат бувы Ц, Г. Оно влючает 2
3
= 8элементов. Событию A
блаоприятствует тольо одна выбора (Ц, Ц, Ц), а событию
B— три: (Ц, Ц, Г), (Ц, Г, Ц), (Г, Ц, Ц). Таим образом, P(A) =
=; P(B) = .
7. . 8. . 9. . 10. . 11. .
См. решение упр. 6.
12. . 13. . 14. . 15. . 16. . 17. .
18. .
Пространство элементарных событий содержит все
перестанови с заданным числом повторений, имеющие со-
став (3, 2, 1). Блаоприятной будет тольо одна таая переста-
нова. 19. . 20. . 21. .
Пространство
элементарных событий содержит все выбори, имеющие состав
(13, 13, 13, 13). Блаоприятными считаются выбори состава
(12, 12, 12, 12), аждой из оторых присоединяется один из
четырех тузов. 22. . 23. . 24. . 25. , ,
, . 26. а) ; б) . 27. = 0,6. 28. .
§ 86. Вычисление вероятностей
геометрическими методами
1. 0,2. 2. . 3. . 4. . 5. . 6. .
Рассмотрите от-
ношение общей площади фиур, ораниченных линиями y = ,
y = 2x, x = 2, y = 0, площади вадрата со стороной 2. 7. – .
См. уазание упр. 6. 8. . Коэффициенты уравнения па-
1
8
---
3
8
---
1
8
---
3
8
---
1
6
---
1
2
---
89
99
------
10
99
------
1
8
---
C
n
2
C
nm+
2
----------------
1
720
----------
245
354
----------
nmk
C
nmk++
3
----------------------- -
C
30
4
C
45
4
---------
4
C
15
2
---------
1
60
------
53!4!⋅
7!
-------------------
24!3!⋅
7!
-------------------
24 48!13
4
⋅
52!
------------------------------
5!5!
10!
-----------
50
C
15
5
---------
C
n
k
C
Nn–
mk–
C
N
m
---------------------- -
1
C
49
6
---------
C
6
5
C
43
1
C
49
6
----------------
C
6
4
C
43
2
C
49
6
----------------
C
6
3
C
43
3
C
49
6
----------------
C
48
5
C
4
1
C
52
6
----------------
C
44
4
C
4
1
C
4
1
C
52
6
------------------------
C
4
2
C
2
1
C
6
3
------------- -
2 C
18
8
⋅
C
20
10
-----------------
r
2
R
2
------ -
1
2
---
2
3
---
1
2
---
13ln2+
8
------------------------- -
1
x
---
1
2
---
π
16
------
2
3
---

628 Ответы, указания, решения
19. Первое, пятое и девятое слааемые разложения. Та
а оэффициенты 1, , образуют арифметичесую
прорессию, то можно составить уравнение
+ 1 = n,
имеющее орни n = 8 и n = 1; n = 1 — посторонний орень.
При n = 8 общий член разложения запишется в виде
T
k
= = 2
k – 8
.
Этот член является рациональным, если k + 8 ратно 4, де 0 m
m k m 8. Уазанное условие выполняется при k = 0, 4, 8. Следо-
вательно, рациональными являются члены T
0
, T
4
, T
8
.
20.
Используйте биномиальное разложение для .
23.
Рассмотрите биномиальное разложение для .
25. Найдите приращения первообразной фунции (1 + x)
n
на
промежуте [0; 1] непосредственно и записав выражение для
по формуле бинома Ньютона. 26.
Найдите производ-
ную фунции в точе x = 1. 27.
Сравните прираще-
ния первообразной фунции на промежуте [0; 1],
найденные непосредственно и с помощью предварительноо раз-
ложения по формуле бинома Ньютона. 28. (n + 1)! – 1.
К исомому выражению прибавьте и отнимите P
1
+ P
2
+ ...
... + P
n
. 29. Используйте тождество + = .
§ 85. Вычисление вероятностей
с помощью формул комбинаторики
1. . 2. . 3. . Количество двузначных чисел равно
90. Количество двузначных чисел, делящихся на 3, найдите из
уравнения 99 = 12 + 3(n – 1). 4. 0,4. 5. .
n
2
---
nn 1–()
8
-----------------------
nn 1–()
8
-----------------------
C
8
k
x
k
2
---
1
2
---
8 k–
x
8 k–
4
---------- ---
x
k 8+
4
---------- --- -
C
8
k
(1 1)
n
–
(10 1)
2n
–
(1 x)
n
+
(x 1)
n
–
(x 1)
n
–
(x 1)
n
–
C
n
k
C
n
k 1–
C
n 1+
k
12
365
----------
5
12
------
1
3
---
3
13
------
Г л а в а 15. Комбинаторика. Элементы теории вероятностей 629
6. P(A) = , P(B) = . Пространство элементарных собы-
тий состоит из таих выборо с повторениями, оторые содер-
жат бувы Ц, Г. Оно влючает 2
3
= 8элементов. Событию A
блаоприятствует тольо одна выбора (Ц, Ц, Ц), а событию
B— три: (Ц, Ц, Г), (Ц, Г, Ц), (Г, Ц, Ц). Таим образом, P(A) =
=; P(B) = .
7. . 8. . 9. . 10. . 11. .
См. решение упр. 6.
12. . 13. . 14. . 15. . 16. . 17. .
18. .
Пространство элементарных событий содержит все
перестанови с заданным числом повторений, имеющие со-
став (3, 2, 1). Блаоприятной будет тольо одна таая переста-
нова. 19. . 20. . 21. .
Пространство
элементарных событий содержит все выбори, имеющие состав
(13, 13, 13, 13). Блаоприятными считаются выбори состава
(12, 12, 12, 12), аждой из оторых присоединяется один из
четырех тузов. 22. . 23. . 24. . 25. , ,
, . 26. а) ; б) . 27. = 0,6. 28. .
§ 86. Вычисление вероятностей
геометрическими методами
1. 0,2. 2. . 3. . 4. . 5. . 6. .
Рассмотрите от-
ношение общей площади фиур, ораниченных линиями y = ,
y = 2x, x = 2, y = 0, площади вадрата со стороной 2. 7. – .
См. уазание упр. 6. 8. . Коэффициенты уравнения па-
1
8
---
3
8
---
1
8
---
3
8
---
1
6
---
1
2
---
89
99
------
10
99
------
1
8
---
C
n
2
C
nm+
2
----------------
1
720
----------
245
354
----------
nmk
C
nmk++
3
----------------------- -
C
30
4
C
45
4
---------
4
C
15
2
---------
1
60
------
53!4!⋅
7!
-------------------
24!3!⋅
7!
-------------------
24 48!13
4
⋅
52!
------------------------------
5!5!
10!
-----------
50
C
15
5
---------
C
n
k
C
Nn–
mk–
C
N
m
---------------------- -
1
C
49
6
---------
C
6
5
C
43
1
C
49
6
----------------
C
6
4
C
43
2
C
49
6
----------------
C
6
3
C
43
3
C
49
6
----------------
C
48
5
C
4
1
C
52
6
----------------
C
44
4
C
4
1
C
4
1
C
52
6
------------------------
C
4
2
C
2
1
C
6
3
------------- -
2 C
18
8
⋅
C
20
10
-----------------
r
2
R
2
------ -
1
2
---
2
3
---
1
2
---
13ln2+
8
------------------------- -
1
x
---
1
2
---
π
16
------
2
3
---

630 Ответы, указания, решения
раболы y = ax
2
+ bx + c найдите из условия прохождения ее
через три уазанные точи, выбрав соответствующую систему
оординат. 9. . 11. При a = 0,5.
Используйте утвержде-
ние упр. 10. 12. d 0,314. 13. 0,5.
Если обозначить расстояние
от точи B до начала оординат через x, а от точи C— через
y, то пространство элементарных событий будет представлено
единичным вадратом, вписанным в первую четверть оорди-
натной плосости. Элементарные события, блаоприятствую-
щие событию, вероятность отороо требуется найти, изобра-
зятся точами, оординаты оторых удовлетворяют неравенст-
ву | y – x | m min{x, y}. 14. Поезд направления AC должен
приходить через 10 мин после отхода поезда направления CA.
15. . Введите систему оординат xOy, де x— уол, ото-
рый образует ила с параллельными прямыми, а y— расстоя-
ние от центра илы до ближайшей прямой. Тода пространству
элементарных событий соответствует прямоуольни со сторо-
нами a и , а элементарным событиям, блаоприятствующим
условию пересечения илой параллельных прямых,— точи,
оординаты оторых удовлетворяют неравенству l sin x < y.
§ 87. Вычисление вероятностей сложных событий
1. ; . 2. ; .
Учтите, что если шары возвращают обратно, то события, свя-
занные с цветом последовательно вынимаемых шаров, незави-
симы. 3. · · d 0,1055. 4. . 5. . 6. а) · ×
× = ; б) . 7. 1 – .
8. . 9. 1 – . 10. 1 – (1 – p)
n
.
11. n >, де n— число выстрелов.
Число выстрелов
найдите из условия, что в серии из n выстрелов вероятность
поражения цели (хотя бы одноо попадания) не меньше P.
12. Вероятность сдачи эзамена не зависит от тоо, идет учени
3π 8–
π
-----------------
2l
πa
------ -
π
2
---
nn 1–()
nm+()nm1–+()
----------------------------------------------------
mm 1–()
nm+()nm1–+()
----------------------------------------------------
n
2
nm+()
2
-----------------------
m
2
nm+()
2
-----------------------
39
51
------
26
50
------
13
49
------
25
216
----------
3
5
---
20
25
------
15
20
------
14
19
------
42
95
------
81
190
----------
6nmk
nmk++()nmk1–++()nmk2–++()
------------------------------------------------------------------------------------------------------------------- -
67
91
------
nl–()nl–1–()... nl– k–1+()
nn 1–()n 2–()... nk–1+()
----------------------------------------------------------------------------------------- -
ln 1 P–()
ln 1 p–()
------------------------- -
Г л а в а 16. Элементы математической логики. Системы счисления 631
отвечать первым или последним. 13. . Рассмотрите следую-
щие ипотезы: A— в урне было два белых шара; B— в урне
было два черных шара; C— в урне были разноцветные шары.
Вероятности ипотез следует считать одинаовыми. 14. 0,85.
15. а) ; б) . 16. .
См. уазание упр. 13.
17.
. [
N
(
N
– 1)(
N
– 2)
×
× (k + L)(k + L – 1)(k + L – 2) – k(k – 1)(k – 2) (N – n)(N – n – 1) ×
× (N – n – 2) – k(k – 1)L(N – n)(N – n – 1)(M – m) – k(L – 1) ×
× (L – 2)(N – n)(M – m)(M – m – 1) – L(L – 1) (L – 2) (M – m) ×
× (M – m – 1) (M – m – 2).
Рассмотрите ипотезы: H
0
— все
три изделия из первой партии; H
1
— два изделия из первой пар-
тии и одно из второй; H
2
— одно изделие из первой партии и
две из второй; H
3
— все три изделия из второй партии.
Г л а в а 16. Элементы математической
логики. Системы счисления
§ 88. Высказывания
6. а) У меня или нет собаи или есть оша; б) у меня нет
ни оши, ни собаи; в) у меня или есть и оша, и собаа или
нет ни оши, ни собаи; ) если у меня нет собаи, то у меня
есть оша.
8. (p , ) # ( , q) # ( , ). 10. а) p º q; б) q º p; в) p J q;
) q º ; д) . 11. . 12. а) Мишень поражена по
райней мере при одном из выстрелов; б) мишень поражена
при аждом выстреле; в)мишень поражена при третьем вы-
стреле, а при одном из первых двух — нет. 13. Да. 14. Все уча-
7.
pqp|q
110
101
011
001
2
3
---
m 1–()mnm+
mn1–+()mn+()
----------------------------------------------------
k 1+()mkn+
kl1++()mn+()
-------------------------------------------------
KnM LmN+
kL+()MN
------------------------------------- -
1
NN 1–()N 2–()kL+()kL1–+()kL2–+()
-----------------------------------------------------------------------------------------------------------------------------
q p p q
p p J q p , q , r

630 Ответы, указания, решения
раболы y = ax
2
+ bx + c найдите из условия прохождения ее
через три уазанные точи, выбрав соответствующую систему
оординат. 9. . 11. При a = 0,5.
Используйте утвержде-
ние упр. 10. 12. d 0,314. 13. 0,5.
Если обозначить расстояние
от точи B до начала оординат через x, а от точи C— через
y, то пространство элементарных событий будет представлено
единичным вадратом, вписанным в первую четверть оорди-
натной плосости. Элементарные события, блаоприятствую-
щие событию, вероятность отороо требуется найти, изобра-
зятся точами, оординаты оторых удовлетворяют неравенст-
ву | y – x | m min{x, y}. 14. Поезд направления AC должен
приходить через 10 мин после отхода поезда направления CA.
15. . Введите систему оординат xOy, де x— уол, ото-
рый образует ила с параллельными прямыми, а y— расстоя-
ние от центра илы до ближайшей прямой. Тода пространству
элементарных событий соответствует прямоуольни со сторо-
нами a и , а элементарным событиям, блаоприятствующим
условию пересечения илой параллельных прямых,— точи,
оординаты оторых удовлетворяют неравенству l sin x < y.
§ 87. Вычисление вероятностей сложных событий
1. ; . 2. ; .
Учтите, что если шары возвращают обратно, то события, свя-
занные с цветом последовательно вынимаемых шаров, незави-
симы. 3. · · d 0,1055. 4. . 5. . 6. а) · ×
× = ; б) . 7. 1 – .
8. . 9. 1 – . 10. 1 – (1 – p)
n
.
11. n >, де n— число выстрелов.
Число выстрелов
найдите из условия, что в серии из n выстрелов вероятность
поражения цели (хотя бы одноо попадания) не меньше P.
12. Вероятность сдачи эзамена не зависит от тоо, идет учени
3π 8–
π
-----------------
2l
πa
------ -
π
2
---
nn 1–()
nm+()nm1–+()
----------------------------------------------------
mm 1–()
nm+()nm1–+()
----------------------------------------------------
n
2
nm+()
2
-----------------------
m
2
nm+()
2
-----------------------
39
51
------
26
50
------
13
49
------
25
216
----------
3
5
---
20
25
------
15
20
------
14
19
------
42
95
------
81
190
----------
6nmk
nmk++()nmk1–++()nmk2–++()
------------------------------------------------------------------------------------------------------------------- -
67
91
------
nl–()nl–1–()... nl– k–1+()
nn 1–()n 2–()... nk–1+()
----------------------------------------------------------------------------------------- -
ln 1 P–()
ln 1 p–()
------------------------- -
Г л а в а 16. Элементы математической логики. Системы счисления 631
отвечать первым или последним. 13. . Рассмотрите следую-
щие ипотезы: A— в урне было два белых шара; B— в урне
было два черных шара; C— в урне были разноцветные шары.
Вероятности ипотез следует считать одинаовыми. 14. 0,85.
15. а) ; б) . 16. .
См. уазание упр. 13.
17.
. [
N
(
N
– 1)(
N
– 2)
×
× (k + L)(k + L – 1)(k + L – 2) – k(k – 1)(k – 2) (N – n)(N – n – 1) ×
× (N – n – 2) – k(k – 1)L(N – n)(N – n – 1)(M – m) – k(L – 1) ×
× (L – 2)(N – n)(M – m)(M – m – 1) – L(L – 1) (L – 2) (M – m) ×
× (M – m – 1) (M – m – 2).
Рассмотрите ипотезы: H
0
— все
три изделия из первой партии; H
1
— два изделия из первой пар-
тии и одно из второй; H
2
— одно изделие из первой партии и
две из второй; H
3
— все три изделия из второй партии.
Г л а в а 16. Элементы математической
логики. Системы счисления
§ 88. Высказывания
6. а) У меня или нет собаи или есть оша; б) у меня нет
ни оши, ни собаи; в) у меня или есть и оша, и собаа или
нет ни оши, ни собаи; ) если у меня нет собаи, то у меня
есть оша.
8. (p , ) # ( , q) # ( , ). 10. а) p º q; б) q º p; в) p J q;
) q º ; д) . 11. . 12. а) Мишень поражена по
райней мере при одном из выстрелов; б) мишень поражена
при аждом выстреле; в)мишень поражена при третьем вы-
стреле, а при одном из первых двух — нет. 13. Да. 14. Все уча-
7.
pqp|q
110
101
011
001
2
3
---
m 1–()mnm+
mn1–+()mn+()
----------------------------------------------------
k 1+()mkn+
kl1++()mn+()
-------------------------------------------------
KnM LmN+
kL+()MN
------------------------------------- -
1
NN 1–()N 2–()kL+()kL1–+()kL2–+()
-----------------------------------------------------------------------------------------------------------------------------
q p p q
p p J q p , q , r
632 Ответы, указания, решения
ствовали. 15. A сдал эзамен. 16. а) (p , q , r) # (p , , r) #
# ( , q , ); б)( , , ); в) .
17. а) (p , q) # ( , ) = p J q; б) p , q; в) , q; ) p , .
18. «Верно ли следующее высазывание: или ты оворишь прав-
ду и этот выход ведет на свободу, или ты лжешь и этот выход
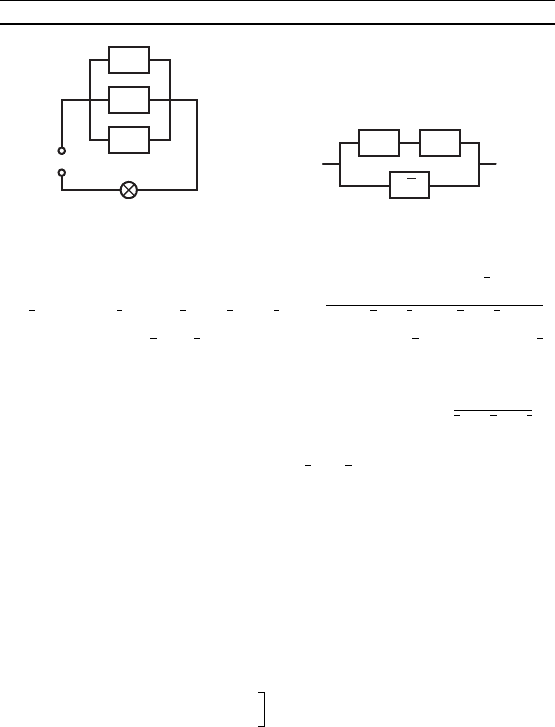
ведет на смерть»? 19. Высазывание имеет вид =
= p # q # r и может быть реализовано в виде схемы, изобра-
женной на рис. 79. 20. (p , q) # (( , ) # q). 21. См. рис. 80.
22. p J q.
§ 89. Предложения, зависящие от переменной
1. а) [–2; +×); б) (2; +×); в) R; ) (–×; –2) Ÿ (2; +×); д) ¾;
е) R. 2. а) R; б) [–2; +×); в) [–2; +×); ) R; д) (–×; –2); е) R.
3. (3; 4). 4. а) 0 < a < ; б) a > . 5. {}. 6. а) a Ý R\{{3} Ÿ {1}};
б) a = 1; в) a = 3. 7. –×; . 8. Истина. 9. Ложь. 10. Исти-
на. 11. Истина. 12. Истина. 13. Ложь. 14. Истина. 15. Ложь.
16. Истина. 17. Ложь. 18. а) (<M > 0) (>n Ý N) (|u
n
| m M);
(>M > 0) (<n Ý N) (|u
n
| > M); б) (>n Ý N) (u
n + 1
> u
n
);
(<n Ý N) (u
n
l u
n + 1
). 19. (>ε > 0) (<δ > 0) (>x Ý R) (0 < |x – a| <
< δ º |f(x) – b| < ε). 20. а) M = f(x) _ (((>x Ý [a; b]) º
º (f(x) m M)) , ((>ε > 0) (<x Ý [a; b]) º (f(x) > M – ε)); б) M −
− f(x) _ ((<x Ý [a; b]) (f(x) > M)) # ((<ε > 0) (>x Ý [a; b])
(f(x) m M – ε); M не является точной верхней ранью фунции
f(x) на отрезе [a; b], если верно одно из двух высазываний:
q
p r p q r (p , q , r) , (p , q , r)
p q p q
p , q , r
p q
p
r
q
pq
p
Рис. 79 Рис. 80
2
3
---
2
3
---
5
2
---
1
2
---
sup
x Ý [a; b]
sup
x Ý [a; b]
Г л а в а 16. Элементы математической логики. Системы счисления 633
или для неотороо x Ý [a; b] справедливо неравенство f(x) > M,
или существует таое ε > 0, что для всех x Ý [a; b] справедливо
неравенство f(x) m M – ε.
§ 91. Системы счисления
1. (114144)
6
. 2. 10 000. 3. 9. 4. 19. 5. 4380; (1540)
4
.
6. (42714)
8
. 7. (3125)
6
. 8. (145244)
6
.
10. 72. 13. Основание системы равно 5. 14. (12)
3
. 15. В лю-
бой системе. 16.
Например, если тело имеет массу 19 , то,
записав число 19 в двоичной системе счисления, имеем (19)
2
=
= (10011)
2
, т. е. для ео взвешивания следует взять следующие
три ири: 2
4
= 16 , 2
1
= 2 и 2
0
= 1 .
17.
Представим любое число, не превосходящее 40, в тро-
ичной системе с цифрами –1, 0, 1 следующим образом: если ос-
тато от деления очередноо неполноо частноо на 3 равен 2,
то пишем (–1) и полученное частное увеличиваем на 1.
Например вместо пишем . Таим образом,
в троичной записи любоо числа будут присутствовать цифры
–1, 0, 1. Продолжая деление в рассматриваемом примере, имеем
Черточа над цифрой 3 означает, что число представлено в сис-
теме с цифрами –1, 0, 1. Та а (40)
10
= (1 1 1 1)
3
, то для лю-
боо тела, масса отороо не превосходит 40 , хватит четырех
ирь с массами 1, 3, 9, 27.
Алоритм взвешивания определяется записью числа в
троичной системе. Та, чтобы взвесить тело в 20 , следует на
одну чашу весов поставить ири с массами 27 = 3
3
и 3 = 3
1
(эти разряды в записи представлены цифрами 1), а на дру-
9.
01
000
101
20 3
(20)
10
= 1 –1 1 –1 .
–1
73
1
23
–1
1
20 3
26
20 3
–1 7
()
3
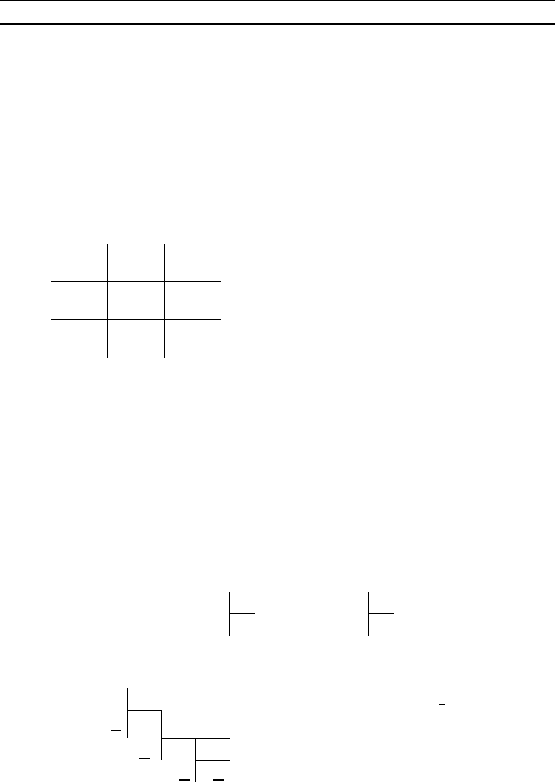
632 Ответы, указания, решения
ствовали. 15. A сдал эзамен. 16. а) (p , q , r) # (p , , r) #
# ( , q , ); б)( , , ); в) .
17. а) (p , q) # ( , ) = p J q; б) p , q; в) , q; ) p , .
18. «Верно ли следующее высазывание: или ты оворишь прав-
ду и этот выход ведет на свободу, или ты лжешь и этот выход
ведет на смерть»? 19. Высазывание имеет вид =
= p # q # r и может быть реализовано в виде схемы, изобра-
женной на рис. 79. 20. (p , q) # (( , ) # q). 21. См. рис. 80.
22. p J q.
§ 89. Предложения, зависящие от переменной
1. а) [–2; +×); б) (2; +×); в) R; ) (–×; –2) Ÿ (2; +×); д) ¾;
е) R. 2. а) R; б) [–2; +×); в) [–2; +×); ) R; д) (–×; –2); е) R.
3. (3; 4). 4. а) 0 < a < ; б) a > . 5. {}. 6. а) a Ý R\{{3} Ÿ {1}};
б) a = 1; в) a = 3. 7. –×; . 8. Истина. 9. Ложь. 10. Исти-
на. 11. Истина. 12. Истина. 13. Ложь. 14. Истина. 15. Ложь.
16. Истина. 17. Ложь. 18. а) (<M > 0) (>n Ý N) (|u
n
| m M);
(>M > 0) (<n Ý N) (|u
n
| > M); б) (>n Ý N) (u
n + 1
> u
n
);
(<n Ý N) (u
n
l u
n + 1
). 19. (>ε > 0) (<δ > 0) (>x Ý R) (0 < |x – a| <
< δ º |f(x) – b| < ε). 20. а) M = f(x) _ (((>x Ý [a; b]) º
º (f(x) m M)) , ((>ε > 0) (<x Ý [a; b]) º (f(x) > M – ε)); б) M −
− f(x) _ ((<x Ý [a; b]) (f(x) > M)) # ((<ε > 0) (>x Ý [a; b])
(f(x) m M – ε); M не является точной верхней ранью фунции
f(x) на отрезе [a; b], если верно одно из двух высазываний:
q
p r p q r (p , q , r) , (p , q , r)
p q p q
p , q , r
p q
p
r
q
pq
p
Рис. 79 Рис. 80
2
3
---
2
3
---
5
2
---
1
2
---
sup
x Ý [a; b]
sup
x Ý [a; b]
Г л а в а 16. Элементы математической логики. Системы счисления 633
или для неотороо x Ý [a; b] справедливо неравенство f(x) > M,
или существует таое ε > 0, что для всех x Ý [a; b] справедливо
неравенство f(x) m M – ε.
§ 91. Системы счисления
1. (114144)
6
. 2. 10 000. 3. 9. 4. 19. 5. 4380; (1540)
4
.
6. (42714)
8
. 7. (3125)
6
. 8. (145244)
6
.
10. 72. 13. Основание системы равно 5. 14. (12)
3
. 15. В лю-
бой системе. 16.
Например, если тело имеет массу 19 , то,
записав число 19 в двоичной системе счисления, имеем (19)
2
=
= (10011)
2
, т. е. для ео взвешивания следует взять следующие
три ири: 2
4
= 16 , 2
1
= 2 и 2
0
= 1 .
17.
Представим любое число, не превосходящее 40, в тро-
ичной системе с цифрами –1, 0, 1 следующим образом: если ос-
тато от деления очередноо неполноо частноо на 3 равен 2,
то пишем (–1) и полученное частное увеличиваем на 1.
Например вместо пишем . Таим образом,
в троичной записи любоо числа будут присутствовать цифры
–1, 0, 1. Продолжая деление в рассматриваемом примере, имеем
Черточа над цифрой 3 означает, что число представлено в сис-
теме с цифрами –1, 0, 1. Та а (40)
10
= (1 1 1 1)
3
, то для лю-
боо тела, масса отороо не превосходит 40 , хватит четырех
ирь с массами 1, 3, 9, 27.
Алоритм взвешивания определяется записью числа в
троичной системе. Та, чтобы взвесить тело в 20 , следует на
одну чашу весов поставить ири с массами 27 = 3
3
и 3 = 3
1
(эти разряды в записи представлены цифрами 1), а на дру-
9.
01
000
101
20 3
(20)
10
= 1 –1 1 –1 .
–1
73
1
23
–1
1
20 3
26
20 3
–1 7
()
3

634 Ответы, указания, решения
ую — с массами 9 = 3
2
и 1=3
0
(эти разряды представлены
цифрами –1).
18.
Масса m
p + 1
следующей ири должна быть не больше
чем 2M
p
+ 1. Действительно, если m
p + 1
> 2M
p
+ 1, то руз мас-
сой M
p
+ 1 удается взвесить с помощью разности m
p
– M
p
. Если
же m
p + 1
< 2M
p + 1
, то масимальная масса M
p + 1
= m
1
+ ...
... + m
p + 1
будет меньше возможной. Следовательно, m
p + 1
можно найти из уравнения
m
p + 1
– M
p
= M
p
+ 1.
Учитывая, что M
p + 1
= m
1
+ ... + m
p + 1
, получаем M
p + 1
=
=3M
p
+ 1.
19.
Нужный результат сразу же следует из утверждения
упр. 18, та а уравнение M
p + 1
= 3M
p
+ 1 поазывает, что при
делении M
p
на 3 для любоо p получается остато, равный 1.
20.
Из результатов упр.19 и 18 следует, что минимальное
число ирь находится из неравенства < n m . Алоритм
взвешивания совпадает с тем, оторый описан в упр. 17 и опре-
деляется записью n в троичной системе счисления.
21.
Если система счисления десятичная, то масимальное
число, оторое можно представить при r = 30, равно 999. Дей-
ствительно, та а p = 3, то 999 — масимальное число, ото-
рое можно записать в десятичной системе счисления с исполь-
зованием трех разрядов.
Если a > 10, например a = 15, то число разрядов p равно 2
и, следовательно, масимальное число равно 15 · 14 + 15
0
· 14 =
= 224. Если основание равно 2, то масимальное число, записан-
ное по этому основанию, равно 2
15
– 1; если основание равно 3,
то 3
10
– 1; если основание равно 6, то 6
5
– 1. Очевидно, что
3
10
– 1 > 2
15
– 1 > 6
5
– 1, та а 9
5
> 8
5
> 6
5
. Ита, маси-
мальным числом является 3
10
– 1.
3
p 1–
3
p
Оглавле ние
От издательства. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Глава 1. Преобразование алгебраических выражений . . . . 5
§ 1. Упрощение иррациональных выражений . . . 6
§ 2. Преобразование выражений, содержащих
зна модуля . . . . . . . . . . . . . . . . . . . . . . . . . . 9
§ 3. Доазательство тождеств . . . . . . . . . . . . . . . . 16
§ 4. Условные тождества. . . . . . . . . . . . . . . . . . . . 19
§ 5. Преобразование лоарифмичесих
выражений . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
Глава 2. Уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
§ 6. Нахождение орней мноочленов . . . . . . . . . 29
§ 7. Рациональные уравнения . . . . . . . . . . . . . . . 37
§ 8. Уравнения, содержащие неизвестное
под знаом модуля . . . . . . . . . . . . . . . . . . . . . 41
§ 9. Иррациональные уравнения . . . . . . . . . . . . . 42
§ 10. Поазательные уравнения . . . . . . . . . . . . . . . 48
§ 11. Лоарифмичесие уравнения. . . . . . . . . . . . . 54
§ 12. Разные задачи . . . . . . . . . . . . . . . . . . . . . . . . 60
Глава 3. Системы уравнений . . . . . . . . . . . . . . . . . . . . . . . 61
§ 13. Системы линейных уравнений. . . . . . . . . . . . 62
§ 14. Системы нелинейных уравнений . . . . . . . . . . 66
§ 15. Системы поазательных и лоарифмичесих
уравнений. . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
§ 16. Разные задачи . . . . . . . . . . . . . . . . . . . . . . . . 81
Глава 4. Неравенства. Уравнения и неравенства
с параметрами . . . . . . . . . . . . . . . . . . . . . . . . . . 82
§ 17. Рациональные и иррациональные
неравенства . . . . . . . . . . . . . . . . . . . . . . . . . . 82
§ 18. Поазательные неравенства . . . . . . . . . . . . . . 90
