Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.

616 Ответы, указания, решения
§ 75. Комбинации многогранников
и фигур вращения
1. . 2. 5:1. 3. 12R
2
. 4. (2+ ):4.
5. a(–1)
2
. 6. R
3
. 7. или .
8. a . 9. R
3
. 10. 4 см. 11. .
12. . 13. . 14. . 15. ×
× ( – 2ctgα). 16. . 17. b 1 + ;
b 1 – . 18. . 19. . 20. π .
21. . 22. ϕ
1
= ; ϕ
2
= 2arctg . 23. .
24. . 25. . 26. . 27. .
28. 4:1. 29. . 30. a
2
(4b
2
– a
2
)
1/2
(4a
2
b
2
– a
4
– b
4
)
–1/2
.
31. . 32. . 33. . 34. . 35. S
бо
=
=3 ( + 1)
2
, α = 2 arcsin . 36. . 37. . 38. 4R
2
×
H
2
2a
2
+
2
------------------------------
3 3
1
4
---
3
2
3
---
2
3
---
35–
2
-----------------
35+
2
------------------
1
8
---
41
8
27
------
3
a
23
-----------
sin 60°
α
2
---
–
sin 60°
α
2
---
+
------------------------------------ -
a cos
α
2
---
2sin
π
3
---
α
2
---
+
sin
π
3
---
α
2
---
–
------------------------------------------------------------------------- -
a
2
-------
a 6
8
-----------
a 3
3
-----------
4ctg
2
α 1+
2π sin
2
α
333 cos
2
α+()
--------------------------------------------
2
3
---
2
3
---
a
22
-----------
a 2ba–()
23b
2
a
2
–
------------------------------ -
4
9
---
ctg
β
2
---
1
3
-------
–
ctg
β
2
---
1
3
-------+
2
---------------------------------------
a 31–()
42
--------------------------
π
3
---
6
3
-------
33sin
2
α cos
4
α
2π
-----------------------------------------------
4π sin
2
α cos α
331 cosα+()
3
--------------------------------------------
4R 3tgα
4tg
2
α+
-----------------------------
a
21 6+()
-------------------------- -
31+
22 3 1++
------------------------------------ -
219b
2
36
-------------------- -
1
2
---
b cos α sin
α
2
---
1cos
α
2
---
+
---------------------------------
Hr
rr
2
4H
2
++
-------------------------------------- -
2
2
-------
a
8
---
15 5
2
5
---
a
6
---
2πa
2
sin
2
2α
--------------------
Г л а в а 13. Стереометрия 617
× sin 2α. 39. 4R
2
cos α (sin α + ). 40. a. 41. rR ×
× (R ä ). 42. R
3
. 43. 2 R
2
cos α×
× (sin α + ). 44. sec
4
. 45. .
46. . 47. a
2
. 48. . 49. .
50. V =4( +1)
3
, α = 2 arcsin . 51. .
52. . 53. S
бо
=; V =· R
3
.
54. . 55. . 56. πl
3
· .
57. V = πR
3
; S
бо
= . 58. π – 4arctg .
59. . 60. S sin α sin 2α cos
2
. 62. 4tg
3
:tgα.
63. 2:1. 64. . 65. arcsin . 66. .
67. . 68. . 69. 2arcsin .
70. . 71.
72. · . 73. 9:16. 74. πR
3
.
75. Rr + R ctg + . 76. . 77. tg – .
cos 2α–
21
6
---------- -
1
6
---
R
2
r
2
–
4
3
---
1cosϕ+()
3
cos ϕ sin
2
ϕ sin α
----------------------------------------------
2
sin
2
α 0,5 cos
2
α+
Q
4
----
α
2
---
a sin α cos α
1cos
2
α+cosα+
------------------------------------------------- -
ab
2a
2
b
2
–
------------------------- -
32 3–()
4
---------------------------- -
c
2cos
α
2
---
cos
β
2
---
+
------------------------------------------------
a 3
41 7+()
------------------------ -
10
11
20
------
a
3
2ba–()
322b
2
a
2
–
-------------------------------------- -
21R
3
16
--------------
83R
2
sin
2
α
------------------ -
43
3
-----------
4sin
2
α–
sin
2
α
--------------------------
32 21
147
------------------
6sin
2
π
2n
-------
1
2
---
n sin
2π
n
------ -
+
3
πn
2
sin
2
2π
n
------ -
--------------------------------------------------------------------
4
3
---
sin
3
α cos
3
α
1cosα+()
3
----------------------------------
2
3
---
4 sin
2
α–
sin
2
α
--------------------------
4πR
2
sin
2
α
----------------
1
2
---
πr
3
ctg
3
π
4
---
α
2
---
–
3cos
2
α sin α
---------------------------------------------
α
2
---
α
2
---
27
16 sin
2
α
------------------------
S
2
S
1
------
R
2
----
3ctg
α
2
---
cosec
2
α
4
---
3
5r
3
-------
r 322 3++()
3
-------------------------------------------- -
1
3
-------
πr
2
rr
2
dr–()
2
++()
3
3 dr–()
2
---------------------------------------------------------------- -
R
r
----
( Rr+ R)
2
.–
Rh
1
h
2
+()
R
2
h
1
2
+ R
2
h
2
2
++
-------------------------------------------------------- -
R
2
h
1
2
+ R–
R
2
h
1
2
+ R+
----------------------------------- -
48
125
----------
π
4
---
α
4
---
4π
9
------ -
2r
3
-------
π
4
---
α
4
---
616 Ответы, указания, решения
§ 75. Комбинации многогранников
и фигур вращения
1. . 2. 5:1. 3. 12R
2
. 4. (2+ ):4.
5. a(–1)
2
. 6. R
3
. 7. или .
8. a . 9. R
3
. 10. 4 см. 11. .
12. . 13. . 14. . 15. ×
× ( – 2ctgα). 16. . 17. b 1 + ;
b 1 – . 18. . 19. . 20. π .
21. . 22. ϕ
1
= ; ϕ
2
= 2arctg . 23. .
24. . 25. . 26. . 27. .
28. 4:1. 29. . 30. a
2
(4b
2
– a
2
)
1/2
(4a
2
b
2
– a
4
– b
4
)
–1/2
.
31. . 32. . 33. . 34. . 35. S
бо
=
=3 ( + 1)
2
, α = 2 arcsin . 36. . 37. . 38. 4R
2
×
H
2
2a
2
+
2
------------------------------
3 3
1
4
---
3
2
3
---
2
3
---
35–
2
-----------------
35+
2
------------------
1
8
---
41
8
27
------
3
a
23
-----------
sin 60°
α
2
---
–
sin 60°
α
2
---
+
------------------------------------ -
a cos
α
2
---
2sin
π
3
---
α
2
---
+
sin
π
3
---
α
2
---
–
------------------------------------------------------------------------- -
a
2
-------
a 6
8
-----------
a 3
3
-----------
4ctg
2
α 1+
2π sin
2
α
333 cos
2
α+()
--------------------------------------------
2
3
---
2
3
---
a
22
-----------
a 2ba–()
23b
2
a
2
–
------------------------------ -
4
9
---
ctg
β
2
---
1
3
-------
–
ctg
β
2
---
1
3
-------+
2
---------------------------------------
a 31–()
42
--------------------------
π
3
---
6
3
-------
33sin
2
α cos
4
α
2π
-----------------------------------------------
4π sin
2
α cos α
331 cosα+()
3
--------------------------------------------
4R 3tgα
4tg
2
α+
-----------------------------
a
21 6+()
-------------------------- -
31+
22 3 1++
------------------------------------ -
219b
2
36
-------------------- -
1
2
---
b cos α sin
α
2
---
1cos
α
2
---
+
---------------------------------
Hr
rr
2
4H
2
++
-------------------------------------- -
2
2
-------
a
8
---
15 5
2
5
---
a
6
---
2πa
2
sin
2
2α
--------------------
Г л а в а 13. Стереометрия 617
× sin 2α. 39. 4R
2
cos α (sin α + ). 40. a. 41. rR ×
× (R ä ). 42. R
3
. 43. 2 R
2
cos α×
× (sin α + ). 44. sec
4
. 45. .
46. . 47. a
2
. 48. . 49. .
50. V =4( +1)
3
, α = 2 arcsin . 51. .
52. . 53. S
бо
=; V =· R
3
.
54. . 55. . 56. πl
3
· .
57. V = πR
3
; S
бо
= . 58. π – 4arctg .
59. . 60. S sin α sin 2α cos
2
. 62. 4tg
3
:tgα.
63. 2:1. 64. . 65. arcsin . 66. .
67. . 68. . 69. 2arcsin .
70. . 71.
72. · . 73. 9:16. 74. πR
3
.
75. Rr + R ctg + . 76. . 77. tg – .
cos 2α–
21
6
---------- -
1
6
---
R
2
r
2
–
4
3
---
1cosϕ+()
3
cos ϕ sin
2
ϕ sin α
----------------------------------------------
2
sin
2
α 0,5 cos
2
α+
Q
4
----
α
2
---
a sin α cos α
1cos
2
α+cosα+
------------------------------------------------- -
ab
2a
2
b
2
–
------------------------- -
32 3–()
4
---------------------------- -
c
2cos
α
2
---
cos
β
2
---
+
------------------------------------------------
a 3
41 7+()
------------------------ -
10
11
20
------
a
3
2ba–()
322b
2
a
2
–
-------------------------------------- -
21R
3
16
--------------
83R
2
sin
2
α
------------------ -
43
3
-----------
4sin
2
α–
sin
2
α
--------------------------
32 21
147
------------------
6sin
2
π
2n
-------
1
2
---
n sin
2π
n
------ -
+
3
πn
2
sin
2
2π
n
------ -
--------------------------------------------------------------------
4
3
---
sin
3
α cos
3
α
1cosα+()
3
----------------------------------
2
3
---
4 sin
2
α–
sin
2
α
--------------------------
4πR
2
sin
2
α
----------------
1
2
---
πr
3
ctg
3
π
4
---
α
2
---
–
3cos
2
α sin α
---------------------------------------------
α
2
---
α
2
---
27
16 sin
2
α
------------------------
S
2
S
1
------
R
2
----
3ctg
α
2
---
cosec
2
α
4
---
3
5r
3
-------
r 322 3++()
3
-------------------------------------------- -
1
3
-------
πr
2
rr
2
dr–()
2
++()
3
3 dr–()
2
---------------------------------------------------------------- -
R
r
----
( Rr+ R)
2
.–
Rh
1
h
2
+()
R
2
h
1
2
+ R
2
h
2
2
++
-------------------------------------------------------- -
R
2
h
1
2
+ R–
R
2
h
1
2
+ R+
----------------------------------- -
48
125
----------
π
4
---
α
4
---
4π
9
------ -
2r
3
-------
π
4
---
α
4
---
618 Ответы, указания, решения
Г л а в а 14. Метод координат
и элементы векторной алгебры
§ 76. Векторы и их координаты
1. а) {–6; –2; 4}; б) {18; –5; 19}; в) {–10; 5; –7}. 2. а) {–30; 21};
б) {0; 0); в) ; ; ) {25; –10}. 3. α = 2, β = 3, γ = 5.
4. а){11; –6; 5}. 5. x = y = z = 1. 6. а) = – ; б) =
= 2 – 3 ; в) = – . 7. а) = {–3; 5; –3}; б) = – ;
; – . 8. 0; . 9. а) (–2; 1); б) (0; 2); в) (0; 2); ) (12; –1).
10. M
1
(7; 0) или M
2
(–1; 0). 11. M(0; 1; 0). 12. M(–1; 0; 0).
13. а) ;1 ; б) ;4 ; в) ; .
Воспользуйтесь тем,
что если вершины треуольниа ABC заданы своими оордина-
тами A(x
1
; y
1
; z
1
), B(x
2
; y
2
; z
2
) и C(x
3
; y
3
; z
3
), то оординаты
центра тяжести G этоо треуольниа находятся по формулам
x = (x
1
+ x
2
+ x
3
), y = (y
1
+ + y
2
+ y
3
), z = (z
1
+ z
2
+ z
3
).
14. а) k = – ; б) k = – ; в) k = –3. 15. а) Да, = ; б) да,
= – . 16. X = – , Y = . 18. (4; 0) и (5; 2). 19. (–1; 2; 4) и
(8; –4; –2). 20. ; ; . 21. При α = –1, β = 4. 26. а) 22;
б) – 200; в) 41; ) . 27. = – ; , = ; – .
28. = ; .
Воспользуйтесь тем, что = + =
= + . 29. –13. 30. а) | | = ; б) | | = . 31. (; ; )
11
2
------
15
2
------
c
a b c
a b c
3
2
---
a PQ PQ
11
10
------
4
3
---
1
6
---
5
2
---
5
3
---
1
3
---
2
3
---
14
3
------
1
3
---
1
3
---
1
3
---
9
14
------
5
16
------
a
3
2
---
b
c
4
3
---
d
5
3
---
6
5
---
11
7
------
10
7
------
18
7
------
105
e
1
3
5
---
4
5
---
e
2
3
5
---
4
5
---
x
21
65
------
77
65
------
x
e
1
e
2
a
a
------
b
b
-----
a 3 b 14 3 3 3
Г л а в а 14. Метод координат и элементы векторной алгебры 619
или (– ; – ; – ). 32. 6. 33. {6; –2; 4} и {–6; 2; –4}.
34. .
Воспользуйтесь тем, что = ( + ) =
= + . 35. а) arccos ; б) arccos – ; в) arccos ;
) arccos – ; д) arccos ; е) arccos – . 36. arccos ;
arccos – ; arccos – ; 135°.
Учтите, что = {1; 0},
={0; 1}. 37. . 38. а) ; ; ; б) 0; – ; – ; в) –1;
0; 0; ) 0; ; .
Учтите, что = {1; 0; 0}, = {0; 1; 0}, =
= {0; 0; 1}. 39. = {–6; 8}. 40. = {–24; –32; 30}. 41. 90°; .
42. = {1; 0; 1} или = – ; ; – .
Положите =
={X; Y; Z}, составьте систему уравнений = 1, = 1,
2
=
2
=
2
= 2 и, решив ее, запишите ответ. 43. cos α =
=cosβ = cos γ = . 44. 135°. 45. При Z = 4. 46. При X = 0,
Y = 2. 47. = {–3; 3; 3}. 48. = ; – ; – . 49. =
= {2; –2; –2}.
Используя перпендиулярность веторов и ,
а таже то, что длина ветора известна, составьте два урав-
нения: X – Y + 2Z = 0, X
2
+ Y
2
+ Z
2
= 12. Замечая, что
| | = | |, запишите еще одно уравнение 2XY + YZ – XZ = 0
и решите систему трех уравнений относительно X, Y, Z.
50. BD = 2 . 51. AC = 5; ; 1; 1 . 52. arccos .
3
3 3 2
85
2
---------- -
AM
1
2
---
AB AC
AB
1
2
---
BC
6
7
---
4
35
-----------
3
7
---
2
14
---------- -
2
7
---
2
35
-----------
2
13
---------- -
2
29
---------- -
5
26
---------- -
i
j
1
11
------
1
3
-------
1
3
-------
1
3
-------
3
10
---------- -
1
10
---------- -
3
5
---
4
5
---
i j k
p b 10
c
1
c
2
1
3
---
4
3
---
1
3
---
c
c a c b
c a b
1
3
-------
c c
4
3
-------
1
3
-------
2
3
-------
a
a d
a
b c
6
5
2
---
63
6441
----------------- -
618 Ответы, указания, решения
Г л а в а 14. Метод координат
и элементы векторной алгебры
§ 76. Векторы и их координаты
1. а) {–6; –2; 4}; б) {18; –5; 19}; в) {–10; 5; –7}. 2. а) {–30; 21};
б) {0; 0); в) ; ; ) {25; –10}. 3. α = 2, β = 3, γ = 5.
4. а){11; –6; 5}. 5. x = y = z = 1. 6. а) = – ; б) =
= 2 – 3 ; в) = – . 7. а) = {–3; 5; –3}; б) = – ;
; – . 8. 0; . 9. а) (–2; 1); б) (0; 2); в) (0; 2); ) (12; –1).
10. M
1
(7; 0) или M
2
(–1; 0). 11. M(0; 1; 0). 12. M(–1; 0; 0).
13. а) ;1 ; б) ;4 ; в) ; .
Воспользуйтесь тем,
что если вершины треуольниа ABC заданы своими оордина-
тами A(x
1
; y
1
; z
1
), B(x
2
; y
2
; z
2
) и C(x
3
; y
3
; z
3
), то оординаты
центра тяжести G этоо треуольниа находятся по формулам
x = (x
1
+ x
2
+ x
3
), y = (y
1
+ + y
2
+ y
3
), z = (z
1
+ z
2
+ z
3
).
14. а) k = – ; б) k = – ; в) k = –3. 15. а) Да, = ; б) да,
= – . 16. X = – , Y = . 18. (4; 0) и (5; 2). 19. (–1; 2; 4) и
(8; –4; –2). 20. ; ; . 21. При α = –1, β = 4. 26. а) 22;
б) – 200; в) 41; ) . 27. = – ; , = ; – .
28. = ; .
Воспользуйтесь тем, что = + =
= + . 29. –13. 30. а) | | = ; б) | | = . 31. (; ; )
11
2
------
15
2
------
c
a b c
a b c
3
2
---
a PQ PQ
11
10
------
4
3
---
1
6
---
5
2
---
5
3
---
1
3
---
2
3
---
14
3
------
1
3
---
1
3
---
1
3
---
9
14
------
5
16
------
a
3
2
---
b
c
4
3
---
d
5
3
---
6
5
---
11
7
------
10
7
------
18
7
------
105
e
1
3
5
---
4
5
---
e
2
3
5
---
4
5
---
x
21
65
------
77
65
------
x
e
1
e
2
a
a
------
b
b
-----
a 3 b 14 3 3 3
Г л а в а 14. Метод координат и элементы векторной алгебры 619
или (– ; – ; – ). 32. 6. 33. {6; –2; 4} и {–6; 2; –4}.
34. .
Воспользуйтесь тем, что = ( + ) =
= + . 35. а) arccos ; б) arccos – ; в) arccos ;
) arccos – ; д) arccos ; е) arccos – . 36. arccos ;
arccos – ; arccos – ; 135°.
Учтите, что = {1; 0},
={0; 1}. 37. . 38. а) ; ; ; б) 0; – ; – ; в) –1;
0; 0; ) 0; ; .
Учтите, что = {1; 0; 0}, = {0; 1; 0}, =
= {0; 0; 1}. 39. = {–6; 8}. 40. = {–24; –32; 30}. 41. 90°; .
42. = {1; 0; 1} или = – ; ; – .
Положите =
={X; Y; Z}, составьте систему уравнений = 1, = 1,
2
=
2
=
2
= 2 и, решив ее, запишите ответ. 43. cos α =
=cosβ = cos γ = . 44. 135°. 45. При Z = 4. 46. При X = 0,
Y = 2. 47. = {–3; 3; 3}. 48. = ; – ; – . 49. =
= {2; –2; –2}.
Используя перпендиулярность веторов и ,
а таже то, что длина ветора известна, составьте два урав-
нения: X – Y + 2Z = 0, X
2
+ Y
2
+ Z
2
= 12. Замечая, что
| | = | |, запишите еще одно уравнение 2XY + YZ – XZ = 0
и решите систему трех уравнений относительно X, Y, Z.
50. BD = 2 . 51. AC = 5; ; 1; 1 . 52. arccos .
3
3 3 2
85
2
---------- -
AM
1
2
---
AB AC
AB
1
2
---
BC
6
7
---
4
35
-----------
3
7
---
2
14
---------- -
2
7
---
2
35
-----------
2
13
---------- -
2
29
---------- -
5
26
---------- -
i
j
1
11
------
1
3
-------
1
3
-------
1
3
-------
3
10
---------- -
1
10
---------- -
3
5
---
4
5
---
i j k
p b 10
c
1
c
2
1
3
---
4
3
---
1
3
---
c
c a c b
c a b
1
3
-------
c c
4
3
-------
1
3
-------
2
3
-------
a
a d
a
b c
6
5
2
---
63
6441
----------------- -
620 Ответы, указания, решения
53. . 54. AA
1
= и BB
1
= ; OG = ; arccos ,
arccos , π –
arccos .
55.
(2 + ; 2+ ) или (2– ;
2– ).
56.
C
1
(3; 6);
D
1
(5; 3) или C
2
(–3; 2), D
2
(–1; –1).
57. A ;, C ;. 58. AA
1
= .
59. D(20; 23; 6). 60. W = 4. 61. W = 7. 62. AB = 5; BC = 5 ;
AC =5; F A = 90°, FB = FC = 45°. 63. Тупоуольный. 64. 45°.
65. = {2; 1}.
Учтите, что B и B , де
=–. 66. . 67. . 68. (0; –2; 0) или
(2; 2; 2).
Зная объем призмы, найдите ее высоту H = AA
1
=
= и, обозначив оординаты вершины A
1
через (x
1
; y
1
; z
1
),
свяжите оординаты ветора = {x – 1; y; z – 1} с ео дли-
ной. Друое уравнение получите из условия B . 69. 18.
70. 26.
§ 77. Аналитическая запись линий на плоскости
и поверхностей в пространстве
1. а) x – y + 1 = 0; б) 3x + 5y – 11 = 0; в) x – 1 = 0; ) y – 2 = 0.
2. 3x – 2y – 12 = 0 или 3x – 8y + 24 = 0.
Воспользуйтесь уравне-
нием прямой в отрезах, т. е. формулой (4). 3. а) 3x – 2y – 5 = 0;
б) x – 5y – = 0. 4. AB: 4x + y – 6 = 0; CD: x – 4y – 2 = 0; h = ;
cos ϕ = ; l
1
: = ; l
2
: ( + 5 ) ×
× (x – 1) + (–4 – 17)(y – 2) = 0. 5. y = 2x – 6, y = –2x + 6.
6. x – 5y + 3 = 0 или 5x + y – 11 = 0. 7. C
1
(5; 10) или C
2
(3; 0).
Площадь треуольниа ABC найдите по формуле
S = | | | | = .
43
25 13
------------------
31
2
------
53
2
---------- -
182
3
--------------
14
15
------
11
56
-----------
5
36
-----------
3 3 3
3
173+
2
--------------------- -
13+
2
------------------
173–
2
---------------------
13–
2
-----------------
3
4
---
10
2
AH AH BC BH AC
BH AH AB
3
2
---
51
3
---------- -
A
1
′
A
1
′′
6
AA
1
AA
1
AC
7
6
---
19
17
---------- -
19
17 58⋅
----------------------
x 1–
26 5 17+
---------------------------------
y 2–
426–17–
------------------------------------- -
26 17
26
1
2
---
a b 1
ab
ab
------------
2
–
1
2
---
ab()
2
ab()
2
–
Г л а в а 14. Метод координат и элементы векторной алгебры 621
8. D(9; 0). 9. (x – 1)
2
+ (y – 1)
2
= 1. 10. y = или y = – .
11. B(12; 5), C(–5; 12), D(–12; –5).
Воспользуйтесь тем, что
точа C симметрична точе A относительно начала оорди-
нат. 12. x – + (y – )
2
= ; x – + (y + )
2
= .
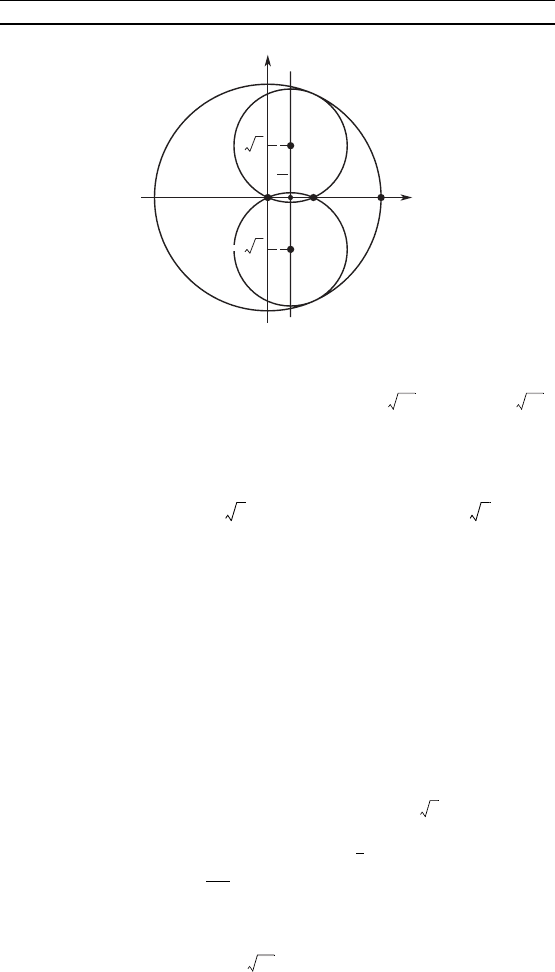
Центр исомой оружности лежит на прямой, проходящей
через точу ; 0 и перпендиулярной оси Ox (рис. 76). Диа-
метр исомой оружности равен радиусу данной. Запишите урав-
нение исомой оружности в виде x – + (y – y
0
)
2
= и
воспользовавшись тем, что она проходит через точу A(1; 0),
найдите y
0
. 13. (x – 1)
2
+ (y – 1)
2
= 1; (x – 5)
2
+ (y – 5)
2
= 25.
14. 2x – y – 2z = 0. 15. а) 3x + 4y + 6z – 29 = 0; б) 2x – 2y – z +
+9 = 0; в)x – y + 4z + 11 = 0; )x – 5y + 9z – 46 = 0.
16. а) arccos ; б) arccos ; в) arccos . 17. .
Сначала
найдите осинус ула между ветором , перпендиулярным
плосости, и ветором . Затем, используя определение ула
между прямой и плосостью, найдите синус этоо ула.
18. а) arcsin ; б) arcsin . 19. 10. 20. а) 1,5; б) 0; в) 4.
x
y
2
1
2
1
A
3
O
–
2
Рис. 76
15
2
---------- -
15
2
---------- -
1
2
---
2
2
9
4
---
1
2
---
2
2
9
4
---
1
2
---
1
2
---
2
9
4
---
5
6
---
5
14
------
5
11
------
6
7
-------
n
AB
18
35
------
23
15 10
------------------
620 Ответы, указания, решения
53. . 54. AA
1
= и BB
1
= ; OG = ; arccos ,
arccos , π –
arccos .
55.
(2 + ; 2+ ) или (2– ;
2– ).
56.
C
1
(3; 6);
D
1
(5; 3) или C
2
(–3; 2), D
2
(–1; –1).
57. A ;, C ;. 58. AA
1
= .
59. D(20; 23; 6). 60. W = 4. 61. W = 7. 62. AB = 5; BC = 5 ;
AC =5; F A = 90°, FB = FC = 45°. 63. Тупоуольный. 64. 45°.
65. = {2; 1}.
Учтите, что B и B , де
=–. 66. . 67. . 68. (0; –2; 0) или
(2; 2; 2).
Зная объем призмы, найдите ее высоту H = AA
1
=
= и, обозначив оординаты вершины A
1
через (x
1
; y
1
; z
1
),
свяжите оординаты ветора = {x – 1; y; z – 1} с ео дли-
ной. Друое уравнение получите из условия B . 69. 18.
70. 26.
§ 77. Аналитическая запись линий на плоскости
и поверхностей в пространстве
1. а) x – y + 1 = 0; б) 3x + 5y – 11 = 0; в) x – 1 = 0; ) y – 2 = 0.
2. 3x – 2y – 12 = 0 или 3x – 8y + 24 = 0.
Воспользуйтесь уравне-
нием прямой в отрезах, т. е. формулой (4). 3. а) 3x – 2y – 5 = 0;
б) x – 5y – = 0. 4. AB: 4x + y – 6 = 0; CD: x – 4y – 2 = 0; h = ;
cos ϕ = ; l
1
: = ; l
2
: ( + 5 ) ×
× (x – 1) + (–4 – 17)(y – 2) = 0. 5. y = 2x – 6, y = –2x + 6.
6. x – 5y + 3 = 0 или 5x + y – 11 = 0. 7. C
1
(5; 10) или C
2
(3; 0).
Площадь треуольниа ABC найдите по формуле
S = | | | | = .
43
25 13
------------------
31
2
------
53
2
---------- -
182
3
--------------
14
15
------
11
56
-----------
5
36
-----------
3 3 3
3
173+
2
--------------------- -
13+
2
------------------
173–
2
---------------------
13–
2
-----------------
3
4
---
10
2
AH AH BC BH AC
BH AH AB
3
2
---
51
3
---------- -
A
1
′
A
1
′′
6
AA
1
AA
1
AC
7
6
---
19
17
---------- -
19
17 58⋅
----------------------
x 1–
26 5 17+
---------------------------------
y 2–
426–17–
------------------------------------- -
26 17
26
1
2
---
a b 1
ab
ab
------------
2
–
1
2
---
ab()
2
ab()
2
–
Г л а в а 14. Метод координат и элементы векторной алгебры 621
8. D(9; 0). 9. (x – 1)
2
+ (y – 1)
2
= 1. 10. y = или y = – .
11. B(12; 5), C(–5; 12), D(–12; –5).
Воспользуйтесь тем, что
точа C симметрична точе A относительно начала оорди-
нат. 12. x – + (y – )
2
= ; x – + (y + )
2
= .
Центр исомой оружности лежит на прямой, проходящей
через точу ; 0 и перпендиулярной оси Ox (рис. 76). Диа-
метр исомой оружности равен радиусу данной. Запишите урав-
нение исомой оружности в виде x – + (y – y
0
)
2
= и
воспользовавшись тем, что она проходит через точу A(1; 0),
найдите y
0
. 13. (x – 1)
2
+ (y – 1)
2
= 1; (x – 5)
2
+ (y – 5)
2
= 25.
14. 2x – y – 2z = 0. 15. а) 3x + 4y + 6z – 29 = 0; б) 2x – 2y – z +
+9 = 0; в)x – y + 4z + 11 = 0; )x – 5y + 9z – 46 = 0.
16. а) arccos ; б) arccos ; в) arccos . 17. .
Сначала
найдите осинус ула между ветором , перпендиулярным
плосости, и ветором . Затем, используя определение ула
между прямой и плосостью, найдите синус этоо ула.
18. а) arcsin ; б) arcsin . 19. 10. 20. а) 1,5; б) 0; в) 4.
x
y
2
1
2
1
A
3
O
–
2
Рис. 76
15
2
---------- -
15
2
---------- -
1
2
---
2
2
9
4
---
1
2
---
2
2
9
4
---
1
2
---
1
2
---
2
9
4
---
5
6
---
5
14
------
5
11
------
6
7
-------
n
AB
18
35
------
23
15 10
------------------
622 Ответы, указания, решения
21. 3. 22. 6x + 2y + 3z ä 42 = 0. 23. (–1; 0; 2). 24. а) (0; 0; –2);
б) (2; 3; 1). 25. 3.
Воспользуйтесь тем, что ветор = {2; 2; –1}
параллелен прямой, проходящей через центр сферы перпенди-
улярно данной плосости. Расстояние от центра сферы до
плосости равно 5. 26. (4; –3; 0) и ; ; . 27. x – +
+(y – 1)
2
+ (z – 1)
2
= – ; при m
2
> — сфера; при
m
2
=— точа; при m
2
< — пустое множество.
§ 78. Решение геометрических задач
с помощью метода координат
1. arccos . 2. π – arccos . 3. arccos . 4. arccos .
5. .
Выберите систему оординат xOy та, чтобы оси Ox и Oy
проходили соответственно через атеты BC и BA. 7. 2ax + 2by =
= a
2
+ b
2
, де a, b— длины атетов. Выберите прямоуоль-
ную систему оординат та, чтобы ось Ox совпала с атетом
CA, а ось Oy — с атетом CB. 14. 3a
2
, де a— длина стороны
вадрата. 15. 4a
2
, де a— длина стороны вадрата. 16. .
17. . 18. . 19. . 20. . 21. arccos .
22. .
Введем систему
оординат Oxyz, а поазано на
рис. 77, и найдем оординаты то-
че A, E и F: A(a; 0; 0), E 0; ; a ,
F ; a; a . Уравнение плосости,
проходящей через эти точи, име-
ет вид x + y + z + a = 0. Далее
найдем осинус ула между плос-
n
4
21
------
97
21
------
40
21
------
3
2
---
2
m
2
2
------- -
33
4
------
33
2
------
33
2
------
33
2
------
3
14
---------- -
1
513
-------------- -
3
10
---------- -
1
5
-------
1
3
---
6
170
--------------
3
170
--------------
1
3
---
1121
170
-------------
551
850
----------
1
4
---
1373
85
-------------
7
3
-------
D
1
E
F
N
K
D
C
B
B
1
C
1
A
1
A
y
z
x
Рис. 77
7a
2
17
24
---------------------
a
2
---
a
2
---
3
2
---
Г л а в а 14. Метод координат и элементы векторной алгебры 623
остью нижнео основания и данной плосостью: cos ϕ = .
Площадь проеции пятиуольниа, полученноо в сечении у-
ба сеущей плосостью, на плосость нижнео основания уба
равна S
пр
= a
2
– = , и, следовательно, площадь самоо
пятиуольниа S = = .
23. A
1
K = A
1
L = a, KL = a; 7 : 41. Из условия следу-
ет, что K ; 0; 0 , L 0; a; (рис. 78). Поэтому A
1
L
2
= a
2
+
+ = , т. е. A
1
L = , A
1
K
2
= + a
2
, т. е. A
1
K = .
Рассмотрим две треуольные пирамиды: NAKA
1
и NDML. Не-
известные длины ребер ND и DM второй пирамиды обозначим
через x и y соответственно. Из подобия треуольниов A
1
NA и
LND следует, что x = a, а из подобия треуольниов AKN и
DMN — что y = ; тода KL
2
= + a
2
+ = , отуда
KL = . Значит, = · · · a · 2a = , V
NDML
=
= · · · · a = . Отсюда находим объем одной из
частей уба, на оторые разбивает ео сеущая плосость:
3
17
---------- -
a
2
8
------
7a
2
8
--------- -
S
пр
cos ϕ
-------------
717a
2
24
---------------------
A
1
D
1
L
M
N
K
D
C
B
B
1
C
1
A
y
z
x
Рис. 78
5
2
-------
6
2
-------
a
2
---
a
2
---
a
2
4
------
5a
2
4
--------- -
a 5
2
-----------
a
2
4
------
a 5
2
-----------
a
4
---
a
2
4
------
a
2
4
------
3a
2
2
--------- -
a 6
2
-----------
V
NAKA
1
1
3
---
1
2
---
a
2
---
a
3
6
------
1
3
---
1
2
---
a
2
---
a
4
---
a
3
48
------

622 Ответы, указания, решения
21. 3. 22. 6x + 2y + 3z ä 42 = 0. 23. (–1; 0; 2). 24. а) (0; 0; –2);
б) (2; 3; 1). 25. 3.
Воспользуйтесь тем, что ветор = {2; 2; –1}
параллелен прямой, проходящей через центр сферы перпенди-
улярно данной плосости. Расстояние от центра сферы до
плосости равно 5. 26. (4; –3; 0) и ; ; . 27. x – +
+(y – 1)
2
+ (z – 1)
2
= – ; при m
2
> — сфера; при
m
2
=— точа; при m
2
< — пустое множество.
§ 78. Решение геометрических задач
с помощью метода координат
1. arccos . 2. π – arccos . 3. arccos . 4. arccos .
5. .
Выберите систему оординат xOy та, чтобы оси Ox и Oy
проходили соответственно через атеты BC и BA. 7. 2ax + 2by =
= a
2
+ b
2
, де a, b— длины атетов. Выберите прямоуоль-
ную систему оординат та, чтобы ось Ox совпала с атетом
CA, а ось Oy — с атетом CB. 14. 3a
2
, де a— длина стороны
вадрата. 15. 4a
2
, де a— длина стороны вадрата. 16. .
17. . 18. . 19. . 20. . 21. arccos .
22. .
Введем систему
оординат Oxyz, а поазано на
рис. 77, и найдем оординаты то-
че A, E и F: A(a; 0; 0), E 0; ; a ,
F ; a; a . Уравнение плосости,
проходящей через эти точи, име-
ет вид x + y + z + a = 0. Далее
найдем осинус ула между плос-
n
4
21
------
97
21
------
40
21
------
3
2
---
2
m
2
2
------- -
33
4
------
33
2
------
33
2
------
33
2
------
3
14
---------- -
1
513
-------------- -
3
10
---------- -
1
5
-------
1
3
---
6
170
--------------
3
170
--------------
1
3
---
1121
170
-------------
551
850
----------
1
4
---
1373
85
-------------
7
3
-------
D
1
E
F
N
K
D
C
B
B
1
C
1
A
1
A
y
z
x
Рис. 77
7a
2
17
24
---------------------
a
2
---
a
2
---
3
2
---
Г л а в а 14. Метод координат и элементы векторной алгебры 623
остью нижнео основания и данной плосостью: cos ϕ = .
Площадь проеции пятиуольниа, полученноо в сечении у-
ба сеущей плосостью, на плосость нижнео основания уба
равна S
пр
= a
2
– = , и, следовательно, площадь самоо
пятиуольниа S = = .
23. A
1
K = A
1
L = a, KL = a; 7 : 41. Из условия следу-
ет, что K ; 0; 0 , L 0; a; (рис. 78). Поэтому A
1
L
2
= a
2
+
+ = , т. е. A
1
L = , A
1
K
2
= + a
2
, т. е. A
1
K = .
Рассмотрим две треуольные пирамиды: NAKA
1
и NDML. Не-
известные длины ребер ND и DM второй пирамиды обозначим
через x и y соответственно. Из подобия треуольниов A
1
NA и
LND следует, что x = a, а из подобия треуольниов AKN и
DMN — что y = ; тода KL
2
= + a
2
+ = , отуда
KL = . Значит, = · · · a · 2a = , V
NDML
=
= · · · · a = . Отсюда находим объем одной из
частей уба, на оторые разбивает ео сеущая плосость:
3
17
---------- -
a
2
8
------
7a
2
8
--------- -
S
пр
cos ϕ
-------------
717a
2
24
---------------------
A
1
D
1
L
M
N
K
D
C
B
B
1
C
1
A
y
z
x
Рис. 78
5
2
-------
6
2
-------
a
2
---
a
2
---
a
2
4
------
5a
2
4
--------- -
a 5
2
-----------
a
2
4
------
a 5
2
-----------
a
4
---
a
2
4
------
a
2
4
------
3a
2
2
--------- -
a 6
2
-----------
V
NAKA
1
1
3
---
1
2
---
a
2
---
a
3
6
------
1
3
---
1
2
---
a
2
---
a
4
---
a
3
48
------
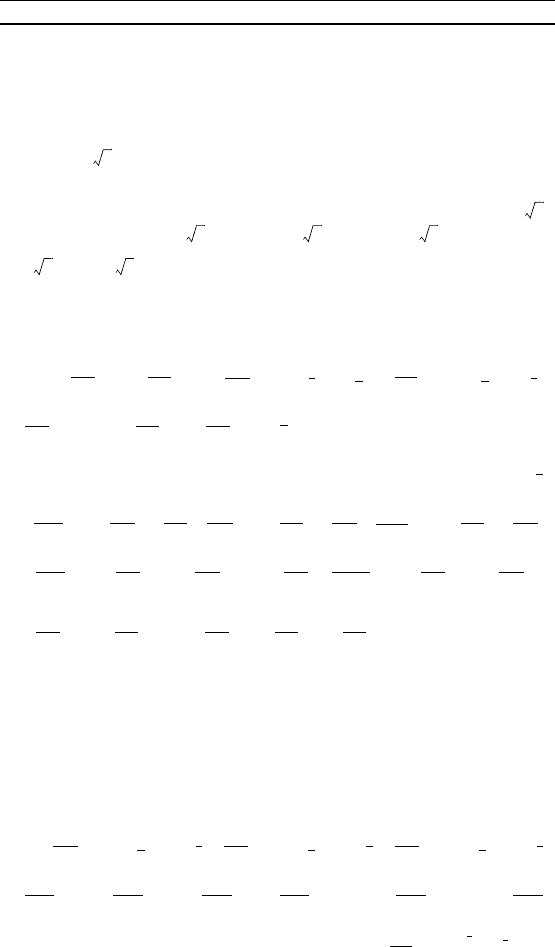
624 Ответы, указания, решения
V
1
= – V
NDML
= . Поэтому объем второй части уба
равен V
2
= a
3
, отуда V
1
: V
2
= 7 : 41.
24. . 25. а) ; б) . 26. 8a
2
, де a— длина сто-
роны уба. 27. 90°; . 28. 45°; . 29. 60°; . 30. а) ;
б) . 31. .
§ 79. Простейшие задачи векторной алгебры
1. –( + 2 ). 2. = 2( – ), = ( + ).
3. = ( + n ). 4. . 6. λ
1
= 3; λ
2
= –2. 7. λ = .
8. λ = , µ = . 9. k
1
= 1, k
2
= –2. 11. p = q = 1. 12. .
13. = – , = – , = ( – ).
14. = – + + , = – – +
+. 15. = ( + + ). 16. –; ; .
17. ;
;
. 18. ;
;
. 19. 1; ; . 20. 1; ;
–.
§ 80. Решение геометрических задач
методами векторной алгебры
4. = + , = + , = + .
5. = + . 6. = + .
17. 4. 18. 2 : 11. 19. 3 : 2. 20. 25 : 64. 21. = , де
V
NAKA
1
7a
3
48
--------- -
41
48
------
3a
2
3
4
------------------
a
2
4
------
7a
2
32
--------- -
2
3
-------
1
3
-------
1
3
-------
a 5
3
-----------
a 5
5
-----------
a 2
2
-----------
DC CQ BD b a AC
2
3
---
a b
AO
1
1 n+
------------- -
AB AD 0
1
3
---
10
7
------
4
7
---
0
AM
1
2
---
OB OA BN
1
2
---
OC OB MN
1
2
---
OC OB
AM BA
1
2
---
BB
1
1
2
---
BC A
1
M BA
1
2
---
BB
1
1
2
---
BC AA
1
1
3
---
BA
1
CB
1
AC
1
1
2
---
1
2
---
3
2
---
1
3
---
1
3
---
1
3
---
7
10
------
3
20
------
3
20
------
1
2
---
1
2
---
1
2
---
2
3
---
DC
1
3
4
---
a
1
4
---
b DC
2
1
2
---
a
1
2
---
b DC
3
1
4
---
a
3
4
---
b
MC
2
3
---
MA
1
3
---
MB MC
1
k 1+
--------------
MA
k
k 1+
--------------
MB
AA
1
cb bc+
bc+
-------------------
Г л а в а 15. Комбинаторика. Элементы теории вероятностей 625
= , = и | | = b, | | = c. 22. 1 : 2. 23. 1 : 3.
24. . 31. 1 : 8. 32. 3. 33. 8 : 37. 34. 1 : 6.
§ 81. Задачи, решаемые с помощью
скалярного произведения векторов
1. а) 9; б) 13; в) –61. 2. –13. 3. Веторы и долж-
ны быть взаимно перпендиулярны. 5. k = – . 8. а) m
a
=
=; б)l
a
= . 9. а) m
a
=
=; б)l
a
= , де p = .
10. arctg . 11. (3 + ) : 8. 12. . 24. При FA = FB = 30°,
FC = 120°.
Г л а в а 15. Комбинаторика. Бином Ньютона.
Элементы теории вероятностей
§ 82. Размещения, сочетания, перестановки
1. 10
7
номеров. Из исходноо множества (0, 1, 2, ..., 9)
производятся выбори с повторениями, содержащие по
7 элементов. 2. номеров.
Найдите сумму чисел,
представляющих собой оличество различных выборо по
одному, двум, ..., семи элементам исходноо множества.
3. 243 бувы. 4. 2
32
жителей. 5. Количество делителей числа q
равно произведению (k
1
+ 1) (k
2
+ 1) ... (k
m
+ 1). 6. номеров.
7. 2
n
исходов. Воспользуйтесь тем, что данное множество со-
стоит из двух элементов (Г, Ц), а выбори с повторениями —
из n элементов. 8. 720 перестаново. 9. а) 2 · 29! способами;
б) 28 · 29! способами. 10. 968 аордов.
Найдите сумму чи-
сел различных аордов, содержащих по три, четыре, ...,
десять звуов. Один аорд, состоящий из k звуов, пред-
ставляет собой выбору k элементов из исходноо множества,
AC
b AB c AC AB
ab+()bc+()abc++()
ab a b 2c++()
-----------------------------------------------------------------
a b
a · b
a · c
----------- -
1
2
---
b
2
2bc cos Ac
2
++
2bc cos A/2()
bc+
------------------------------------- -
1
2
---
a
2
–2b
2
2c
2
++
2 bcp p a–()
bc+
------------------------------------
abc++
2
-----------------------
2
2
-------
73
2
7
-------
10 10
7
1–()
9
--------------------------------
A
10
7

624 Ответы, указания, решения
V
1
= – V
NDML
= . Поэтому объем второй части уба
равен V
2
= a
3
, отуда V
1
: V
2
= 7 : 41.
24. . 25. а) ; б) . 26. 8a
2
, де a— длина сто-
роны уба. 27. 90°; . 28. 45°; . 29. 60°; . 30. а) ;
б) . 31. .
§ 79. Простейшие задачи векторной алгебры
1. –( + 2 ). 2. = 2( – ), = ( + ).
3. = ( + n ). 4. . 6. λ
1
= 3; λ
2
= –2. 7. λ = .
8. λ = , µ = . 9. k
1
= 1, k
2
= –2. 11. p = q = 1. 12. .
13. = – , = – , = ( – ).
14. = – + + , = – – +
+. 15. = ( + + ). 16. –; ; .
17. ;
;
. 18. ;
;
. 19. 1; ; . 20. 1; ;
–.
§ 80. Решение геометрических задач
методами векторной алгебры
4. = + , = + , = + .
5. = + . 6. = + .
17. 4. 18. 2 : 11. 19. 3 : 2. 20. 25 : 64. 21. = , де
V
NAKA
1
7a
3
48
--------- -
41
48
------
3a
2
3
4
------------------
a
2
4
------
7a
2
32
--------- -
2
3
-------
1
3
-------
1
3
-------
a 5
3
-----------
a 5
5
-----------
a 2
2
-----------
DC CQ BD b a AC
2
3
---
a b
AO
1
1 n+
------------- -
AB AD 0
1
3
---
10
7
------
4
7
---
0
AM
1
2
---
OB OA BN
1
2
---
OC OB MN
1
2
---
OC OB
AM BA
1
2
---
BB
1
1
2
---
BC A
1
M BA
1
2
---
BB
1
1
2
---
BC AA
1
1
3
---
BA
1
CB
1
AC
1
1
2
---
1
2
---
3
2
---
1
3
---
1
3
---
1
3
---
7
10
------
3
20
------
3
20
------
1
2
---
1
2
---
1
2
---
2
3
---
DC
1
3
4
---
a
1
4
---
b DC
2
1
2
---
a
1
2
---
b DC
3
1
4
---
a
3
4
---
b
MC
2
3
---
MA
1
3
---
MB MC
1
k 1+
--------------
MA
k
k 1+
--------------
MB
AA
1
cb bc+
bc+
-------------------
Г л а в а 15. Комбинаторика. Элементы теории вероятностей 625
= , = и | | = b, | | = c. 22. 1 : 2. 23. 1 : 3.
24. . 31. 1 : 8. 32. 3. 33. 8 : 37. 34. 1 : 6.
§ 81. Задачи, решаемые с помощью
скалярного произведения векторов
1. а) 9; б) 13; в) –61. 2. –13. 3. Веторы и долж-
ны быть взаимно перпендиулярны. 5. k = – . 8. а) m
a
=
=; б)l
a
= . 9. а) m
a
=
=; б)l
a
= , де p = .
10. arctg . 11. (3 + ) : 8. 12. . 24. При FA = FB = 30°,
FC = 120°.
Г л а в а 15. Комбинаторика. Бином Ньютона.
Элементы теории вероятностей
§ 82. Размещения, сочетания, перестановки
1. 10
7
номеров. Из исходноо множества (0, 1, 2, ..., 9)
производятся выбори с повторениями, содержащие по
7 элементов. 2. номеров.
Найдите сумму чисел,
представляющих собой оличество различных выборо по
одному, двум, ..., семи элементам исходноо множества.
3. 243 бувы. 4. 2
32
жителей. 5. Количество делителей числа q
равно произведению (k
1
+ 1) (k
2
+ 1) ... (k
m
+ 1). 6. номеров.
7. 2
n
исходов. Воспользуйтесь тем, что данное множество со-
стоит из двух элементов (Г, Ц), а выбори с повторениями —
из n элементов. 8. 720 перестаново. 9. а) 2 · 29! способами;
б) 28 · 29! способами. 10. 968 аордов.
Найдите сумму чи-
сел различных аордов, содержащих по три, четыре, ...,
десять звуов. Один аорд, состоящий из k звуов, пред-
ставляет собой выбору k элементов из исходноо множества,
AC
b AB c AC AB
ab+()bc+()abc++()
ab a b 2c++()
-----------------------------------------------------------------
a b
a · b
a · c
----------- -
1
2
---
b
2
2bc cos Ac
2
++
2bc cos A/2()
bc+
------------------------------------- -
1
2
---
a
2
–2b
2
2c
2
++
2 bcp p a–()
bc+
------------------------------------
abc++
2
-----------------------
2
2
-------
73
2
7
-------
10 10
7
1–()
9
--------------------------------
A
10
7
