Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


40 Г л а в а 2. Уравнения
введением вспомоательноо неизвестноо
y = cx + .
П р и м е р 4. Решить уравнение
+ = 1.
Р е ш е н и е. Подстановой убеждаемся в том, что x = 0
не является орнем исходноо уравнения. Разделив числитель
и знаменатель аждой дроби на x, получаем эвивалентное
уравнение
+ = 1.
Полаая x + = y, приходим уравнению
+ = 1,
сводящемуся вадратному уравнению, орнями отороо яв-
ляются y
1
= 0, y
2
= 3.
Таим образом, исходное уравнение эвивалентно двум урав-
нениям
x + = 0, x + = 3,
первое из оторых не имеет действительных орней, а орни
второо — числа x
1,2
= .
Ответ. x
1, 2
= .
Решите уравнение:
18. + = 6.
19. – = .
20. + = .
d
x
---
x
x
2
x–1+
---------------------------
2x
x
2
x 1++
----------------------------
1
x
1
x
---
1–+
----------------------- -
2
x
1
x
---
1++
------------------------
1
x
---
1
y 1–
-------------
2
y 1+
-------------
1
x
---
1
x
---
3 ä 5
2
---------------- -
3 ä 5
2
---------------- -
2x
2x
2
5x–3+
---------------------------------- -
13x
2x
2
x 3++
-------------------------------
3x
x
2
14x–+
-------------------------------
2x
x
2
1 x++
----------------------------
8
3
---
3x
2
1–
x
--------------------
5x
3x
2
x–1–
------------------------------
119
18
----------
§ 8. Уравнения, содержащие неизвестное под знаком модуля 41
§ 8. Уравнения, содержащие
неизвестное под знаком модуля
Если в уравнении неоторые выражения, содержащие неиз-
вестное, находятся под знаом модуля, то решение исходноо
уравнения следует исать отдельно на аждом из промежутов
знаопостоянства этих выражений.
П р и м е р 1. Решить уравнение
|2x – 5| = x – 1.
Р е ш е н и е. Выражение 2x – 5, записанное под знаом мо-
дуля, неотрицательно при x l 2,5 и отрицательно при x < 2,5.
Рассмотрим исходное уравнение отдельно на аждом из этих
промежутов.
Пусть x l 2,5. Тода по определению модуля имеем |2x – 5| =
= 2x – 5, и данное уравнение примет вид
2x – 5 = x – 1.
Решив это уравнение, находим x = 4. Та а число 4 принад-
лежит рассматриваемому промежуту, то x = 4 является реше-
нием исходноо уравнения.
Пусть теперь x < 2,5. Тода по определению модуля имеем
|2x – 5| = –(2x – 5), и данное уравнение примет вид
–(2x – 5) = x – 1.
Решив это уравнение, находим x = 2. Та а число 2 при-
надлежит рассматриваемому промежуту, то x = 2 является
решением исходноо уравнения.
Ответ. x
1
= 2, x
2
= 4.
П р и м е р 2. Решить уравнение
|x – 1| – 2|x – 2| + 3|x – 3| = 4.
Р е ш е н и е. Данное уравнение эвивалентно следующим
уравнениям:
1) 1 – x + 2(x – 2) – 3(x – 3) = 4 при x m 1;
2) x – 1 + 2(x – 2) – 3(x – 3) = 4 при 1 < x m 2;
3) x – 1 – 2(x – 2) – 3(x – 3) = 4 при 2 < x m 3;
4) x – 1 – 2(x – 2) + 3(x – 3) = 4 при x > 3.
Первое уравнение имеет решение x = 1; второе уравнение
обращается в тождество для всех значений x, удовлетворяю-

40 Г л а в а 2. Уравнения
введением вспомоательноо неизвестноо
y = cx + .
П р и м е р 4. Решить уравнение
+ = 1.
Р е ш е н и е. Подстановой убеждаемся в том, что x = 0
не является орнем исходноо уравнения. Разделив числитель
и знаменатель аждой дроби на x, получаем эвивалентное
уравнение
+ = 1.
Полаая x + = y, приходим уравнению
+ = 1,
сводящемуся вадратному уравнению, орнями отороо яв-
ляются y
1
= 0, y
2
= 3.
Таим образом, исходное уравнение эвивалентно двум урав-
нениям
x + = 0, x + = 3,
первое из оторых не имеет действительных орней, а орни
второо — числа x
1,2
= .
Ответ. x
1, 2
= .
Решите уравнение:
18. + = 6.
19. – = .
20. + = .
d
x
---
x
x
2
x–1+
---------------------------
2x
x
2
x 1++
----------------------------
1
x
1
x
---
1–+
----------------------- -
2
x
1
x
---
1++
------------------------
1
x
---
1
y 1–
-------------
2
y 1+
-------------
1
x
---
1
x
---
3 ä 5
2
---------------- -
3 ä 5
2
---------------- -
2x
2x
2
5x–3+
---------------------------------- -
13x
2x
2
x 3++
-------------------------------
3x
x
2
14x–+
-------------------------------
2x
x
2
1 x++
----------------------------
8
3
---
3x
2
1–
x
--------------------
5x
3x
2
x–1–
------------------------------
119
18
----------
§ 8. Уравнения, содержащие неизвестное под знаком модуля 41
§ 8. Уравнения, содержащие
неизвестное под знаком модуля
Если в уравнении неоторые выражения, содержащие неиз-
вестное, находятся под знаом модуля, то решение исходноо
уравнения следует исать отдельно на аждом из промежутов
знаопостоянства этих выражений.
П р и м е р 1. Решить уравнение
|2x – 5| = x – 1.
Р е ш е н и е. Выражение 2x – 5, записанное под знаом мо-
дуля, неотрицательно при x l 2,5 и отрицательно при x < 2,5.
Рассмотрим исходное уравнение отдельно на аждом из этих
промежутов.
Пусть x l 2,5. Тода по определению модуля имеем |2x – 5| =
= 2x – 5, и данное уравнение примет вид
2x – 5 = x – 1.
Решив это уравнение, находим x = 4. Та а число 4 принад-
лежит рассматриваемому промежуту, то x = 4 является реше-
нием исходноо уравнения.
Пусть теперь x < 2,5. Тода по определению модуля имеем
|2x – 5| = –(2x – 5), и данное уравнение примет вид
–(2x – 5) = x – 1.
Решив это уравнение, находим x = 2. Та а число 2 при-
надлежит рассматриваемому промежуту, то x = 2 является
решением исходноо уравнения.
Ответ. x
1
= 2, x
2
= 4.
П р и м е р 2. Решить уравнение
|x – 1| – 2|x – 2| + 3|x – 3| = 4.
Р е ш е н и е. Данное уравнение эвивалентно следующим
уравнениям:
1) 1 – x + 2(x – 2) – 3(x – 3) = 4 при x m 1;
2) x – 1 + 2(x – 2) – 3(x – 3) = 4 при 1 < x m 2;
3) x – 1 – 2(x – 2) – 3(x – 3) = 4 при 2 < x m 3;
4) x – 1 – 2(x – 2) + 3(x – 3) = 4 при x > 3.
Первое уравнение имеет решение x = 1; второе уравнение
обращается в тождество для всех значений x, удовлетворяю-
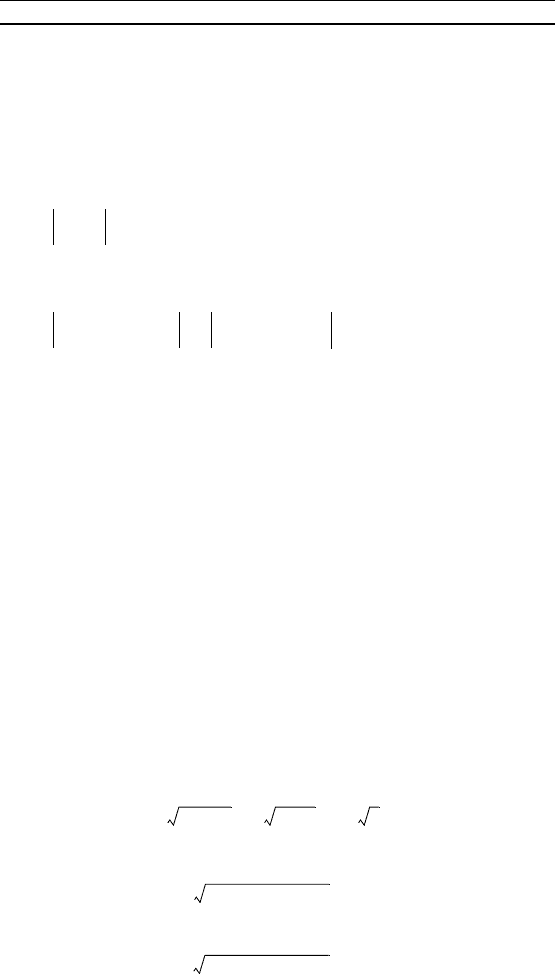
42 Г л а в а 2. Уравнения
щих неравенствам 1 < x m 2; третье не имеет решений; четвер-
тое имеет решение x = 5.
Ответ. x Ý [1; 2], x = 5.
Решите уравнение:
1. |x| = x + 2. 2. |–x + 2| = 2x + 1.
3. |x – 1| + |x – 2| = 1. 4. |2 – |1 – |x||| = 1.
5. = 1. 6. |x
2
– 1| = –|x| + 1.
7. |5x – x
2
– 6| = x
2
– 5x + 6.
8. |x – 1| + |x + 2| – |x – 3| = 4.
9. x
2
– 2x + + x
2
– 3x + 4 = .
§ 9. Иррациональные уравнения
Иррациональным равнением называют уравнение, в о-
тором неизвестная величина содержится под знаом радиала.
Область допустимых значений иррациональноо уравнения со-
стоит из тех значений неизвестноо, при оторых неотрица-
тельны все выражения, находящиеся под знаами радиалов
четной степени.
Метод возведения равнения в степень. Один из способов
решения иррациональноо уравнения залючается в последо-
вательном возведении обеих частей уравнения в степень, яв-
ляющуюся наименьшим общим ратным поазателей всех ра-
диалов, входящих в данное уравнение. Если степень, в ото-
рую возводится уравнение, четная, то полученное уравнение
может иметь орни, не являющиеся орнями исходноо урав-
нения. В этом случае необходима провера орней.
П р и м е р 1. Решить уравнение
+ = 2 . (*)
Р е ш е н и е. Возведем обе части данноо уравнения в
вадрат:
3x + 4 + 2 + x – 4 = 4x. (**)
Приведя подобные члены, получаем уравнение
2 = 0,
x 1+
x 1–
------------- -
1
2
---
3
2
---
1
2
---
3
4
---
3x 4+ x 4– x
3x 4+()x 4–()
3x 4+()x 4–()
§ 9. Иррациональные уравнения 43
орнями отороо являются x = – и x = 4. Один из получен-
ных орней, а именно x = – , не удовлетворяет исходному
уравнению, та а не входит в область ео допустимых значе-
ний. Проверой убеждаемся, что при x = 4 исходное уравнение
обращается в тождество.
Ответ. x = 4.
Решите уравнение:
1. = 8 – .
2. + = 4.
3. – = 2.
4. – = 2.
5. = 2 – .
6. + = 3.
7. + = 5.
8. = + 1.
9. (x
2
– 4) = 0.
10. + = .
11. + = .
12. + = 3.
13. + = 4.
14. + = 2.
15. – x + 3 = 0.
16. – = 1.
17. – = 2.
18. + = .
19. + = .
20. + = .
4
3
---
4
3
---
x 1+ 3x 1+
xx11++ xx11+–
17 x+ 17 x–
3x 7+ x 1+
25 x– 9 x+
x
2
1+ x
2
2x–3+
x
2
x 5–+ x
2
8x 4–+
x
2
x 1++ x
2
x–1+
x 1+
4x 3– 5x 1+ 15x 4+
x 5+ x 3+ 2x 7+
4 x– 5 x+
4x 2+ 4x 2–
xx2–– xx2–+
x 7+
x 34+
3
x 3–
3
2x 5+ 3x 5–
x
3
x 16–
3
x 8–
3
x 5+
3
x 6+
3
2x 11+
3
x 1+
3
3x 1+
3
x 1–
3

42 Г л а в а 2. Уравнения
щих неравенствам 1 < x m 2; третье не имеет решений; четвер-
тое имеет решение x = 5.
Ответ. x Ý [1; 2], x = 5.
Решите уравнение:
1. |x| = x + 2. 2. |–x + 2| = 2x + 1.
3. |x – 1| + |x – 2| = 1. 4. |2 – |1 – |x||| = 1.
5. = 1. 6. |x
2
– 1| = –|x| + 1.
7. |5x – x
2
– 6| = x
2
– 5x + 6.
8. |x – 1| + |x + 2| – |x – 3| = 4.
9. x
2
– 2x + + x
2
– 3x + 4 = .
§ 9. Иррациональные уравнения
Иррациональным равнением называют уравнение, в о-
тором неизвестная величина содержится под знаом радиала.
Область допустимых значений иррациональноо уравнения со-
стоит из тех значений неизвестноо, при оторых неотрица-
тельны все выражения, находящиеся под знаами радиалов
четной степени.
Метод возведения равнения в степень. Один из способов
решения иррациональноо уравнения залючается в последо-
вательном возведении обеих частей уравнения в степень, яв-
ляющуюся наименьшим общим ратным поазателей всех ра-
диалов, входящих в данное уравнение. Если степень, в ото-
рую возводится уравнение, четная, то полученное уравнение
может иметь орни, не являющиеся орнями исходноо урав-
нения. В этом случае необходима провера орней.
П р и м е р 1. Решить уравнение
+ = 2 . (*)
Р е ш е н и е. Возведем обе части данноо уравнения в
вадрат:
3x + 4 + 2 + x – 4 = 4x. (**)
Приведя подобные члены, получаем уравнение
2 = 0,
x 1+
x 1–
------------- -
1
2
---
3
2
---
1
2
---
3
4
---
3x 4+ x 4– x
3x 4+()x 4–()
3x 4+()x 4–()
§ 9. Иррациональные уравнения 43
орнями отороо являются x = – и x = 4. Один из получен-
ных орней, а именно x = – , не удовлетворяет исходному
уравнению, та а не входит в область ео допустимых значе-
ний. Проверой убеждаемся, что при x = 4 исходное уравнение
обращается в тождество.
Ответ. x = 4.
Решите уравнение:
1. = 8 – .
2. + = 4.
3. – = 2.
4. – = 2.
5. = 2 – .
6. + = 3.
7. + = 5.
8. = + 1.
9. (x
2
– 4) = 0.
10. + = .
11. + = .
12. + = 3.
13. + = 4.
14. + = 2.
15. – x + 3 = 0.
16. – = 1.
17. – = 2.
18. + = .
19. + = .
20. + = .
4
3
---
4
3
---
x 1+ 3x 1+
xx11++ xx11+–
17 x+ 17 x–
3x 7+ x 1+
25 x– 9 x+
x
2
1+ x
2
2x–3+
x
2
x 5–+ x
2
8x 4–+
x
2
x 1++ x
2
x–1+
x 1+
4x 3– 5x 1+ 15x 4+
x 5+ x 3+ 2x 7+
4 x– 5 x+
4x 2+ 4x 2–
xx2–– xx2–+
x 7+
x 34+
3
x 3–
3
2x 5+ 3x 5–
x
3
x 16–
3
x 8–
3
x 5+
3
x 6+
3
2x 11+
3
x 1+
3
3x 1+
3
x 1–
3
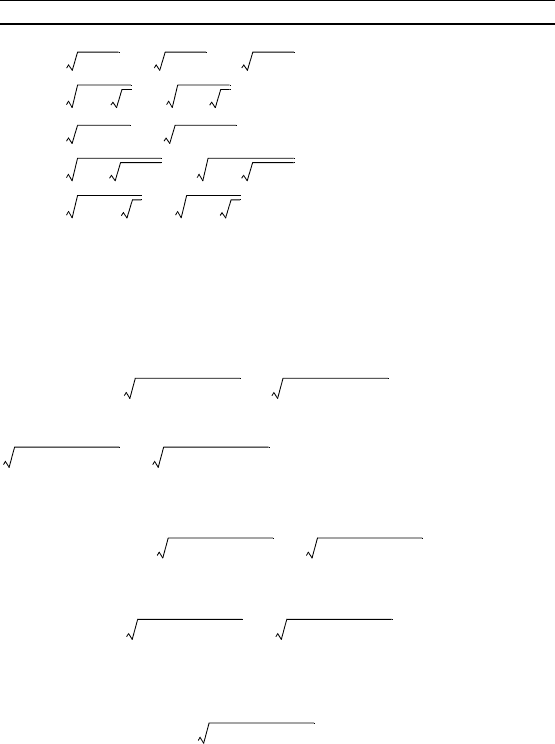
44 Г л а в а 2. Уравнения
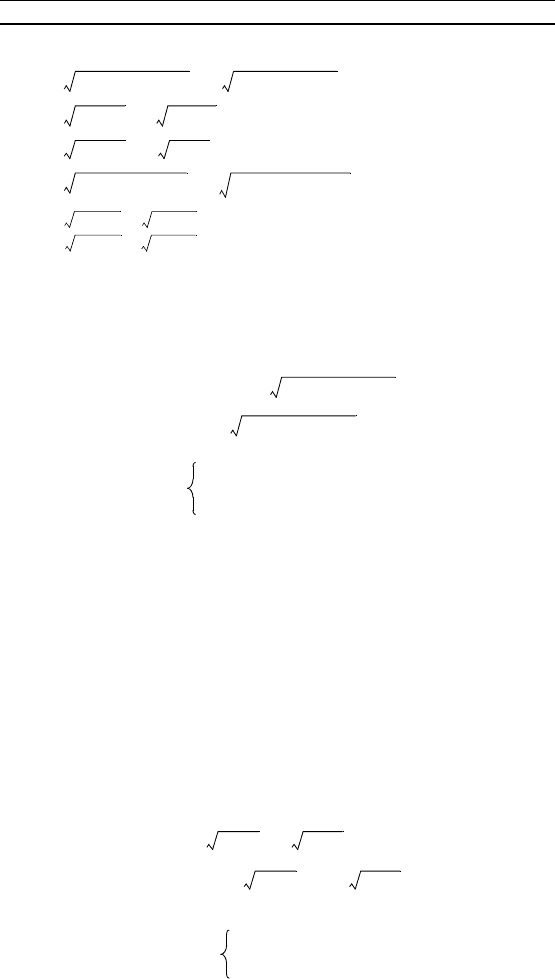
21. + + = 0.
22. + = 2.
23. – = 1.
24. + = 4.
25. – = 1.
Неоторые специальные приемы решения иррациональ-
ных равнений. Инода можно освободиться от иррациональ-
ности умножением обеих частей уравнения на неоторое выра-
жение, не обращающееся в нуль.
П р и м е р 2. Решить уравнение
– = 1. (*)
Р е ш е н и е. Умножим обе части уравнения на выражение
+ , являющееся сопряженным ле-
вой части уравнения (*). После приведения подобных членов
получаем уравнение
7 = + (**)
эвивалентное исходному, та а уравнение
+ = 0
не имеет действительных орней.
Сложив уравнения (*) и (**), получим
= 4.
Возведя последнее уравнение в вадрат, приходим вадрат-
ному уравнению
3x
2
+ 5x – 8 = 0,
имеющему орни x
1
= – , x
2
= 1. Выполнив проверу, убежда-
емся, что оба орня являются орнями исходноо уравнения.
Ответ. x
1
= 1, x
2
= – .
x 1+
3
x 2+
3
x 3+
3
1 x+
3
1 x–
3
5x 7+
3
5x 12–
3
9 x 1+–
3
7 x 1++
3
24 x+
3
5 x+
3
3x
2
5x 8++ 3x
2
5x 1++
3x
2
5x 8++ 3x
2
5x 1++
3x
2
5x 8++ 3x
2
5x 1++,
3x
2
5x 8++ 3x
2
5x 1++
3x
2
5x 8++
8
3
---
8
3
---
§ 9. Иррациональные уравнения 45
Решите уравнение:
26. + = 7.
27. – = 2.
28. + = 6.
29. + = p.
30. = .
В неоторых случаях введение вспомоательных неизвест-
ных позволяет перейти от иррациональноо уравнения систе-
ме рациональных уравнений.
Пример 3. Решить уравнение
x
2
– 4x – 6 = .
Р е ш е н и е. Полаая = y, получим систему
уравнений
(*)
Ислючив из системы (*) неизвестное x, приходим уравнению
y
2
– 2y – 24 = 0.
Ео орнями являются y
1
= 6, y
2
= –4. Та а через y обозна-
чен арифметичесий орень, то из двух найденных орней
уравнения выбираем положительный. Подставляя ео во вто-
рое уравнение системы (*), получаем уравнение
x
2
– 4x – 12 = 0,
орни отороо x
1
= 6, x
2
= –2. Провера поазывает, что оба
орня являются орнями исходноо уравнения.
Ответ. x
1
= 6, x
2
= –2.
П р и м е р 4. Решить уравнение
= .
Р е ш е н и е. Положим = u, = v. Ислючив x
из уравнений u
3
= x + 1, v
2
= x – 3, придем системе
3x
2
2x–15+ 3x
2
2x–8+
x
2
9+ x
2
7–
15 x– 3 x–
Ax
2
Bx C++ Ax
2
Bx C
1
++
21 x+21x–+
21 x+21x––
--------------------------------------------------
21
x
------
2x
2
8x–12+
2x
2
8x–12+
y
2
= 2x
2
– 8x + 12,
y = x
2
– 4x – 6.
x 1+
3
x 3–
x 1+
3
x 3–
u = v,
u
3
– v
2
= 4.
44 Г л а в а 2. Уравнения
21. + + = 0.
22. + = 2.
23. – = 1.
24. + = 4.
25. – = 1.
Неоторые специальные приемы решения иррациональ-
ных равнений. Инода можно освободиться от иррациональ-
ности умножением обеих частей уравнения на неоторое выра-
жение, не обращающееся в нуль.
П р и м е р 2. Решить уравнение
– = 1. (*)
Р е ш е н и е. Умножим обе части уравнения на выражение
+ , являющееся сопряженным ле-
вой части уравнения (*). После приведения подобных членов
получаем уравнение
7 = + (**)
эвивалентное исходному, та а уравнение
+ = 0
не имеет действительных орней.
Сложив уравнения (*) и (**), получим
= 4.
Возведя последнее уравнение в вадрат, приходим вадрат-
ному уравнению
3x
2
+ 5x – 8 = 0,
имеющему орни x
1
= – , x
2
= 1. Выполнив проверу, убежда-
емся, что оба орня являются орнями исходноо уравнения.
Ответ. x
1
= 1, x
2
= – .
x 1+
3
x 2+
3
x 3+
3
1 x+
3
1 x–
3
5x 7+
3
5x 12–
3
9 x 1+–
3
7 x 1++
3
24 x+
3
5 x+
3
3x
2
5x 8++ 3x
2
5x 1++
3x
2
5x 8++ 3x
2
5x 1++
3x
2
5x 8++ 3x
2
5x 1++,
3x
2
5x 8++ 3x
2
5x 1++
3x
2
5x 8++
8
3
---
8
3
---
§ 9. Иррациональные уравнения 45
Решите уравнение:
26. + = 7.
27. – = 2.
28. + = 6.
29. + = p.
30. = .
В неоторых случаях введение вспомоательных неизвест-
ных позволяет перейти от иррациональноо уравнения систе-
ме рациональных уравнений.
Пример 3. Решить уравнение
x
2
– 4x – 6 = .
Р е ш е н и е. Полаая = y, получим систему
уравнений
(*)
Ислючив из системы (*) неизвестное x, приходим уравнению
y
2
– 2y – 24 = 0.
Ео орнями являются y
1
= 6, y
2
= –4. Та а через y обозна-
чен арифметичесий орень, то из двух найденных орней
уравнения выбираем положительный. Подставляя ео во вто-
рое уравнение системы (*), получаем уравнение
x
2
– 4x – 12 = 0,
орни отороо x
1
= 6, x
2
= –2. Провера поазывает, что оба
орня являются орнями исходноо уравнения.
Ответ. x
1
= 6, x
2
= –2.
П р и м е р 4. Решить уравнение
= .
Р е ш е н и е. Положим = u, = v. Ислючив x
из уравнений u
3
= x + 1, v
2
= x – 3, придем системе
3x
2
2x–15+ 3x
2
2x–8+
x
2
9+ x
2
7–
15 x– 3 x–
Ax
2
Bx C++ Ax
2
Bx C
1
++
21 x+21x–+
21 x+21x––
--------------------------------------------------
21
x
------
2x
2
8x–12+
2x
2
8x–12+
y
2
= 2x
2
– 8x + 12,
y = x
2
– 4x – 6.
x 1+
3
x 3–
x 1+
3
x 3–
u = v,
u
3
– v
2
= 4.

46 Г л а в а 2. Уравнения
Ее решение сводится решению уравнения
v
3
– v
2
– 4 = 0,
имеющему единственный действительный орень v = 2. Воз-
вращаясь исходному неизвестному, получаем линейное урав-
нение 4 = x – 3, орень отороо является единственным ор-
нем исходноо уравнения.
Ответ. x = 7.
Решите уравнение:
31. + 8 = 7.
32. + = x
2
– 6x + 11.
33. + = 4.
34. (x + 4) (x + 1) – 3 = 6.
35. + = 2,5.
36. – 2 = 3.
37. = x + – 6.
38. + = 2.
39. – = 56.
40. = 2.
41. x – 4 + 4 = 0.
42. x
2
+ 3x – 18 + 4 = 0.
43. + = 2 .
44. – = 5.
45. = 1.
46. + = 7 .
47. (x – 3)
2
+ 3x – 22 = .
48. = .
7x 3–()
3
5
37x–()
3–
5
x 2– 4 x–
47 2x–
4
35 2x+
4
x
2
5x 2++
16z
z 1–
------------ -
5
z 1–
16z
------------ -
5
x
2
32+ x
2
32+
4
x 4+ x 4–+
2
-------------------------------------------
x
2
16–
5 x–
x 3+
--------------
7
x 3+
5 x–
--------------
7
xx
5
xx
5
5 x–()5 x– x 3–()x 3–+
5 x– x 3–+
-------------------------------------------------------------------------------- -
x
3
x
2
3
x
2
3x 6–+
3y
2
6y 16++ y
2
2y+ y
2
2y 4++
x
2
66
2
+ x+
x
--------------------------------------
xx
2
66
2
+ x
2
–
3 x 2–()42x
2
3x–1++
2 x
2
1–()
------------------------------------------------------------------------ -
x 2–2x 5–+ x 232x 5–++ 2
x
2
3x–7+
3 x+
3x
------------- -
1
9
---
1
x
---
4
9
---
2
x
2
------
++
§ 9. Иррациональные уравнения 47
Метод выделения полноо вадрата в подоренных выра-
жениях.
Пример 5. Решить уравнение
– = 1.
Р е ш е н и е. Положим = t; тода исходное уравне-
ние примет вид
– = 1. (*)
Та а под знаами радиалов в левой части уравнения (*) на-
ходятся полные вадраты, то уазанное уравнение сводится
следующему:
|t + 1| – |t – 1| = 1. (**)
Уравнение (**) имеет единственный орень t = 0,5. Возвраща-
ясь исходному неизвестному, получаем уравнение
= 0,5,
орнем отороо является x = 2,25.
Ответ. x = 2,25.
Решите уравнение:
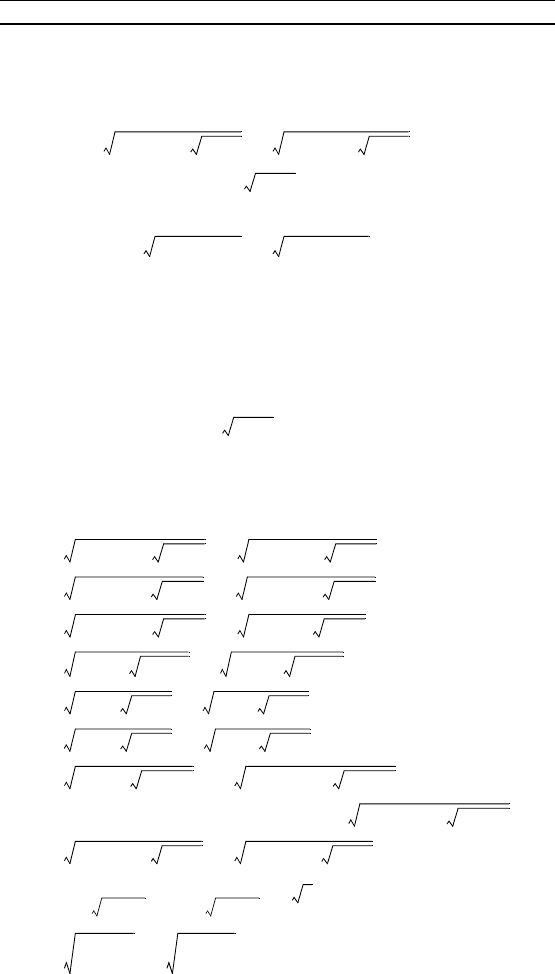
49. + = 2.
50. + = 1.
51. + = 4.
52. – = 1.
53. – = 3.
54. + = x – 1.
55. – 2 +
+ 3 = 4.
56. + = 1.
57. – = .
58. + = x
2
.
x 1–2x 2–+
x 1–2x 2––
x 2–
t
2
2t 1++ t
2
2t–1+
x 2–
x 22x 1+++ x 22x 1+–+
x 54x 1+–+ x 22x 1+–+
x 82x 7+++ x 1 x 7+–+
x
2
2 x
2
1–+ x
2
2 x
2
1––
x 2 x 1–+ x 2 x 1––
x 2 x 1–+ x 2 x 1––
2x 22x 1–– 2x 342x 1––+
2x 862x 1––+
x 34x 1––+ x 86x 1––+
1
xx
2
x––
-------------------------------
1
xx
2
x–+
-------------------------------
3
12
12
x
2
------
– x
2
12
x
2
------
–
46 Г л а в а 2. Уравнения
Ее решение сводится решению уравнения
v
3
– v
2
– 4 = 0,
имеющему единственный действительный орень v = 2. Воз-
вращаясь исходному неизвестному, получаем линейное урав-
нение 4 = x – 3, орень отороо является единственным ор-
нем исходноо уравнения.
Ответ. x = 7.
Решите уравнение:
31. + 8 = 7.
32. + = x
2
– 6x + 11.
33. + = 4.
34. (x + 4) (x + 1) – 3 = 6.
35. + = 2,5.
36. – 2 = 3.
37. = x + – 6.
38. + = 2.
39. – = 56.
40. = 2.
41. x – 4 + 4 = 0.
42. x
2
+ 3x – 18 + 4 = 0.
43. + = 2 .
44. – = 5.
45. = 1.
46. + = 7 .
47. (x – 3)
2
+ 3x – 22 = .
48. = .
7x 3–()
3
5
37x–()
3–
5
x 2– 4 x–
47 2x–
4
35 2x+
4
x
2
5x 2++
16z
z 1–
------------ -
5
z 1–
16z
------------ -
5
x
2
32+ x
2
32+
4
x 4+ x 4–+
2
-------------------------------------------
x
2
16–
5 x–
x 3+
--------------
7
x 3+
5 x–
--------------
7
xx
5
xx
5
5 x–()5 x– x 3–()x 3–+
5 x– x 3–+
-------------------------------------------------------------------------------- -
x
3
x
2
3
x
2
3x 6–+
3y
2
6y 16++ y
2
2y+ y
2
2y 4++
x
2
66
2
+ x+
x
--------------------------------------
xx
2
66
2
+ x
2
–
3 x 2–()42x
2
3x–1++
2 x
2
1–()
------------------------------------------------------------------------ -
x 2–2x 5–+ x 232x 5–++ 2
x
2
3x–7+
3 x+
3x
------------- -
1
9
---
1
x
---
4
9
---
2
x
2
------
++
§ 9. Иррациональные уравнения 47
Метод выделения полноо вадрата в подоренных выра-
жениях.
Пример 5. Решить уравнение
– = 1.
Р е ш е н и е. Положим = t; тода исходное уравне-
ние примет вид
– = 1. (*)
Та а под знаами радиалов в левой части уравнения (*) на-
ходятся полные вадраты, то уазанное уравнение сводится
следующему:
|t + 1| – |t – 1| = 1. (**)
Уравнение (**) имеет единственный орень t = 0,5. Возвраща-
ясь исходному неизвестному, получаем уравнение
= 0,5,
орнем отороо является x = 2,25.
Ответ. x = 2,25.
Решите уравнение:
49. + = 2.
50. + = 1.
51. + = 4.
52. – = 1.
53. – = 3.
54. + = x – 1.
55. – 2 +
+ 3 = 4.
56. + = 1.
57. – = .
58. + = x
2
.
x 1–2x 2–+
x 1–2x 2––
x 2–
t
2
2t 1++ t
2
2t–1+
x 2–
x 22x 1+++ x 22x 1+–+
x 54x 1+–+ x 22x 1+–+
x 82x 7+++ x 1 x 7+–+
x
2
2 x
2
1–+ x
2
2 x
2
1––
x 2 x 1–+ x 2 x 1––
x 2 x 1–+ x 2 x 1––
2x 22x 1–– 2x 342x 1––+
2x 862x 1––+
x 34x 1––+ x 86x 1––+
1
xx
2
x––
-------------------------------
1
xx
2
x–+
-------------------------------
3
12
12
x
2
------
– x
2
12
x
2
------
–
48 Г л а в а 2. Уравнения
59. 2 – = .
60. + 3 = .
61. – = .
62. + = 3 + .
63. + = 2x + 2.
64. + = 2.
65. x = ( – 1) ( + 1).
66. + = .
67. + 4 = 5 .
68. + = 4 .
69. + = .
70. = 30.
71. + – = 3.
§ 10. Показательные уравнения
Поазательным равнением называют уравнение, в ото-
ром неизвестное входит тольо в поазатель степени, а основа-
ние степени является постоянным. Простейшее поазательное
уравнение — это уравнение вида
a
x
= b.(1)
Ео решением при a > 0, a − 1 и b > 0 является
x = log
a
b.
Если поазатель степени представляет собой неоторую
фунцию f(x), т. е. уравнение имеет вид
a
f(x)
= b, a > 0, a − 1, b > 0, (2)
5 x 1+
4
4+ 2 x 1+
4
1– 20 x 1+
4
5+
2x
2
9x–4+ 2x 1– 2x
2
21x 11–+
4x
2
9x 5++ 2x
2
x 1–+ x
2
1–
44x– x
2
+
3
49 14xx
2
++
3
14 5x– x
2
–
3
2x
2
8x 6++ x
2
1–
x 2– 1 x–
1
4
---
1 x+ 1 x–
1
x 2 x 1–+
------------------------------------
1
x 2 x 1––
------------------------------------
2
2 x–
-------------
ax+()
2
3
ax–()
2
3
a
2
x
2
–
3
x 1+()
2
n
x 1–()
2
n
x
2
1–
n
x
2
8x+
x 1+
-------------------------
x 7+
7
x 1+
------------------
34 x–()x 1+
3
x 1+()34 x–
3
–
34 x–
3
x 1+
3
–
--------------------------------------------------------------------------------------------
2 x–()
2
3
7 x+()
2
3
2 x–()7 x+()
3
§ 10. Показательные уравнения 49
то, лоарифмируя обе части этоо уравнения, приходим эви-
валентному уравнению
f(x) = log
a
b.
Сведение простейшим поазательным равнениям. Не-
оторые поазательные уравнения приводятся виду (1) или (2)
с помощью равенств
a
x
· a
y
= a
x + y
,
(a
x
)
y
= a
xy
,
= a
x – y
,
=
=
де a и b— любые положительные числа, а x и y— любые дей-
ствительные числа.
П р и м е р 1. Решить уравнение
= ·
Р е ш е н и е. Перепишем данное уравнение в виде
· = ·
Используя свойство членов пропорции, имеем
= ,
или после упрощения 3
4 – x
= 2
4 – x
. Преобразуя данное уравне-
ние виду
= 1,
получаем 4 – x = 0, отуда следует, что x = 4.
Ответ. x = 4.
Решите уравнение:
1. · = 225. 2. · = 1600.
3. 9
3 – 5x
· 7
5x – 3
= 1. 4. 3
2x – 1
· 5
3x + 2
= · 5
2x
· 3
3x
.
a
x
a
y
------
(a · b)
x
a
x
·b
x
,
a
b
---
x
a
x
b
x
------ ,
6
2x 4+
3
3x
2
x 8+
.
3
2x 4+
2
2x 4+
3
3x
2
x 8+
.
3
2x 4+
3
3x
-----------------
2
x 8+
2
2x 4+
-----------------
2
3
---
4 x–
3
x
5
x
2
3x
5
x
9
5
---

48 Г л а в а 2. Уравнения
59. 2 – = .
60. + 3 = .
61. – = .
62. + = 3 + .
63. + = 2x + 2.
64. + = 2.
65. x = ( – 1) ( + 1).
66. + = .
67. + 4 = 5 .
68. + = 4 .
69. + = .
70. = 30.
71. + – = 3.
§ 10. Показательные уравнения
Поазательным равнением называют уравнение, в ото-
ром неизвестное входит тольо в поазатель степени, а основа-
ние степени является постоянным. Простейшее поазательное
уравнение — это уравнение вида
a
x
= b.(1)
Ео решением при a > 0, a − 1 и b > 0 является
x = log
a
b.
Если поазатель степени представляет собой неоторую
фунцию f(x), т. е. уравнение имеет вид
a
f(x)
= b, a > 0, a − 1, b > 0, (2)
5 x 1+
4
4+ 2 x 1+
4
1– 20 x 1+
4
5+
2x
2
9x–4+ 2x 1– 2x
2
21x 11–+
4x
2
9x 5++ 2x
2
x 1–+ x
2
1–
44x– x
2
+
3
49 14xx
2
++
3
14 5x– x
2
–
3
2x
2
8x 6++ x
2
1–
x 2– 1 x–
1
4
---
1 x+ 1 x–
1
x 2 x 1–+
------------------------------------
1
x 2 x 1––
------------------------------------
2
2 x–
-------------
ax+()
2
3
ax–()
2
3
a
2
x
2
–
3
x 1+()
2
n
x 1–()
2
n
x
2
1–
n
x
2
8x+
x 1+
-------------------------
x 7+
7
x 1+
------------------
34 x–()x 1+
3
x 1+()34 x–
3
–
34 x–
3
x 1+
3
–
--------------------------------------------------------------------------------------------
2 x–()
2
3
7 x+()
2
3
2 x–()7 x+()
3
§ 10. Показательные уравнения 49
то, лоарифмируя обе части этоо уравнения, приходим эви-
валентному уравнению
f(x) = log
a
b.
Сведение простейшим поазательным равнениям. Не-
оторые поазательные уравнения приводятся виду (1) или (2)
с помощью равенств
a
x
· a
y
= a
x + y
,
(a
x
)
y
= a
xy
,
= a
x – y
,
=
=
де a и b— любые положительные числа, а x и y— любые дей-
ствительные числа.
П р и м е р 1. Решить уравнение
= ·
Р е ш е н и е. Перепишем данное уравнение в виде
· = ·
Используя свойство членов пропорции, имеем
= ,
или после упрощения 3
4 – x
= 2
4 – x
. Преобразуя данное уравне-
ние виду
= 1,
получаем 4 – x = 0, отуда следует, что x = 4.
Ответ. x = 4.
Решите уравнение:
1. · = 225. 2. · = 1600.
3. 9
3 – 5x
· 7
5x – 3
= 1. 4. 3
2x – 1
· 5
3x + 2
= · 5
2x
· 3
3x
.
a
x
a
y
------
(a · b)
x
a
x
·b
x
,
a
b
---
x
a
x
b
x
------ ,
6
2x 4+
3
3x
2
x 8+
.
3
2x 4+
2
2x 4+
3
3x
2
x 8+
.
3
2x 4+
3
3x
-----------------
2
x 8+
2
2x 4+
-----------------
2
3
---
4 x–
3
x
5
x
2
3x
5
x
9
5
---
