Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


20 Г л а в а 1. Преобразование алгебраических выражений
Используя тождество
(a + b)
3
= a
3
+ b
3
+ 3ab(a + b),
имеем
c
3
= –a
3
– b
3
– 3ab(a + b)
или, заменяя a + b на –c,
a
3
+ b
3
+ c
3
= 3abc,
что и требовалось доазать.
1. Доажите, что если a + b + c = 0, то
= · .
2. Поажите, что из равенства
a
2
+ b
2
+ c
2
= ab + bc + ac
следует равенство a = b = c.
3. Доажите, что если a
1/3
+ b
1/3
+ c
1/3
= 0, то
(a + b + c)
3
= 27abc.
4. Доажите, что если
+ + = 1 и + + = 0,
то
+ + = 1.
5. Доажите, что если
+ = a,
то
x
2/3
+ y
2/3
= a
2/3
.
6. Доажите, что если a + b + c = 0, то:
а) (a
2
+ b
2
+ c
2
)
2
= 2(a
4
+ b
4
+ c
4
);
б) 2(a
5
+ b
5
+ c
5
) = 5abc(a
2
+ b
2
+ c
2
);
в) 5(a
3
+ b
3
+ c
3
)(a
2
+ b
2
+ c
2
) = 6(a
5
+ b
5
+ c
5
).
a
5
b
5
c
5
++
5
--------------------------------
a
3
b
3
c
3
++
3
--------------------------------
a
2
b
2
c
2
++
2
--------------------------------
x
a
---
y
b
---
z
c
-- -
a
x
---
b
y
---
c
z
-- -
x
2
a
2
------
y
2
b
2
----- -
z
2
c
2
-----
x
2
x
4
y
2
3
+ y
2
x
2
y
4
3
+
§ 4. Условные тождества 21
7. Доажите, что если − , то из системы уравнений
следует, что α
2
+ β
2
= 0.
8. Доажите, что если x − y, y − z, z − x и
+ + = 0,
то
+ + = 0.
9. Доажите, что если
+ + ... + = p
2
,
+ + ... + = q
2
, p − 0, q − 0,
a
1
b
1
+ a
2
b
2
+ ... + a
n
b
n
= pq,
то
a
1
= λb
1
, a
2
= λb
2
, ..., a
n
= λb
n
, де λ = .
10. Доажите, что если = , то
= .
11. Доажите, что если
= = ,
то
= = .
12. Доажите, что если
x = , y = , z = ,
то
(1 + x)(1 + y)(1 + z) = (1 – x)(1 – y)(1 – z).
x
1
x
2
------
y
1
y
2
----- -
αx
1
+ βx
2
= 0,
αy
1
+ βy
2
= 0
x
yz–
------------
y
zx–
------------ -
z
xy–
-------------
x
yz–()
2
--------------------
y
zx–()
2
-------------------- -
z
xy–()
2
---------------------
a
1
2
a
2
2
a
n
2
b
1
2
b
2
2
b
n
2
p
q
-- -
a
b
---
b
c
-- -
a
2
b
2
+
b
2
c
2
+
-------------------
a
c
---
ay bx–
c
-------------------- -
cx az–
b
--------------------
bz cy–
a
-------------------
x
a
---
y
b
---
z
c
-- -
ab–
ab+
-------------
bc–
bc+
------------ -
ca–
ca+
-------------

20 Г л а в а 1. Преобразование алгебраических выражений
Используя тождество
(a + b)
3
= a
3
+ b
3
+ 3ab(a + b),
имеем
c
3
= –a
3
– b
3
– 3ab(a + b)
или, заменяя a + b на –c,
a
3
+ b
3
+ c
3
= 3abc,
что и требовалось доазать.
1. Доажите, что если a + b + c = 0, то
= · .
2. Поажите, что из равенства
a
2
+ b
2
+ c
2
= ab + bc + ac
следует равенство a = b = c.
3. Доажите, что если a
1/3
+ b
1/3
+ c
1/3
= 0, то
(a + b + c)
3
= 27abc.
4. Доажите, что если
+ + = 1 и + + = 0,
то
+ + = 1.
5. Доажите, что если
+ = a,
то
x
2/3
+ y
2/3
= a
2/3
.
6. Доажите, что если a + b + c = 0, то:
а) (a
2
+ b
2
+ c
2
)
2
= 2(a
4
+ b
4
+ c
4
);
б) 2(a
5
+ b
5
+ c
5
) = 5abc(a
2
+ b
2
+ c
2
);
в) 5(a
3
+ b
3
+ c
3
)(a
2
+ b
2
+ c
2
) = 6(a
5
+ b
5
+ c
5
).
a
5
b
5
c
5
++
5
--------------------------------
a
3
b
3
c
3
++
3
--------------------------------
a
2
b
2
c
2
++
2
--------------------------------
x
a
---
y
b
---
z
c
-- -
a
x
---
b
y
---
c
z
-- -
x
2
a
2
------
y
2
b
2
----- -
z
2
c
2
-----
x
2
x
4
y
2
3
+ y
2
x
2
y
4
3
+
§ 4. Условные тождества 21
7. Доажите, что если − , то из системы уравнений
следует, что α
2
+ β
2
= 0.
8. Доажите, что если x − y, y − z, z − x и
+ + = 0,
то
+ + = 0.
9. Доажите, что если
+ + ... + = p
2
,
+ + ... + = q
2
, p − 0, q − 0,
a
1
b
1
+ a
2
b
2
+ ... + a
n
b
n
= pq,
то
a
1
= λb
1
, a
2
= λb
2
, ..., a
n
= λb
n
, де λ = .
10. Доажите, что если = , то
= .
11. Доажите, что если
= = ,
то
= = .
12. Доажите, что если
x = , y = , z = ,
то
(1 + x)(1 + y)(1 + z) = (1 – x)(1 – y)(1 – z).
x
1
x
2
------
y
1
y
2
----- -
αx
1
+ βx
2
= 0,
αy
1
+ βy
2
= 0
x
yz–
------------
y
zx–
------------ -
z
xy–
-------------
x
yz–()
2
--------------------
y
zx–()
2
-------------------- -
z
xy–()
2
---------------------
a
1
2
a
2
2
a
n
2
b
1
2
b
2
2
b
n
2
p
q
-- -
a
b
---
b
c
-- -
a
2
b
2
+
b
2
c
2
+
-------------------
a
c
---
ay bx–
c
-------------------- -
cx az–
b
--------------------
bz cy–
a
-------------------
x
a
---
y
b
---
z
c
-- -
ab–
ab+
-------------
bc–
bc+
------------ -
ca–
ca+
-------------

22 Г л а в а 1. Преобразование алгебраических выражений
§ 5. Преобразование
логарифмических выражений
Пусть a— положительное число, отличное от единицы, а
M— любое положительное число. Лоарифмом числа M по
основанию a называют таое число, обозначаемое log
a
M, что
= M.
Основные свойства лоарифмов
Пусть a > 0, a − 1, b > 0, c > 0, тода справедливы следую-
щие равенства:
log
a
(bc) = log
a
b + log
a
c,(1)
log
a
= log
a
b – log
a
c,(2)
= log
a
b, (3)
log
a
b = , c − 1, (4)
log
a
b = , b − 1. (5)
При тождественных преобразованиях лоарифмичесих
выражений используют формулы (1)—(5) и определение лоа-
рифма.
П р и м е р 1. Упростить выражение
.
Р е ш е н и е. Соласно формуле (3), имеем
(log
1/a
= (–log
a
= (log
a
,(*)
= = log
a
, (**)
(a
2
– 1) = (a
2
– 1)
1/2
= log
a
. (***)
a
log
a
M
b
c
-- -
log
a
p
b
q
q
p
-- -
log
c
b
log
c
a
---------------
1
log
b
a
---------------
log
a
a
2
1– log
1/a
2
a
2
1–
log
a
2
a
2
1–() log
a
3
a
2
1–
6
-----------------------------------------------------------------------------
a
2
1–)
2
a
2
1–)
2
a
2
1–)
2
log
a
3
a
2
1–
6
log
a
3
()
3
a
2
1–
6
()
3
a
2
1–
log
a
2
log
a
2
()
1/2
a
2
1–
§ 5. Преобразование логарифмических выражений 23
Подставив правые части выражений (*)—(***) в исходную
дробь, находим
= log
a
.
Ответ.log
a
.
Пример 2. Вычислить
+ + .
Р е ш е н и е. Используя формулу (5), имеем
= .
Далее, используя свойства степеней, получим
= = .
Но по определению лоарифма = 5. Таим образом,
= 5
4
= 625.
Аналоично,
= = = = 7
2
= 49,
= = = = 216.
Сладывая найденные числа, получаем ответ.
Ответ.890.
Упростите выражение:
1. .
2. – + .
3. : .
4. log
3
2log
4
3log
5
4log
6
5log
7
6log
8
7.
5. log
2
2x
2
+ log
2
x + + .
6. · .
log
a
a
2
1– log
a
2
a
2
1–
log
a
a
2
1– log
a
a
2
1–
---------------------------------------------------------------------
a
2
1–
a
2
1–
81
1/log
5
3
27
log
9
36
3
4/log
7
9
81
1/log
5
3
81
log
3
5
81
log
3
5
3
4
()
log
3
5
3
log
3
5
()
4
3
log
3
5
81
1/log
5
3
3
4/log
7
9
3
4log
9
7
3
2
()
2log
9
7
9
log
9
7
()
2
27
log
9
36
27
log
3
6
3
3log
3
6
3
log
3
6
()
3
81
1/log
5
9
3
3/log
6
3
+
409
------------------------------------------------------
7()
2/log
25
7
125
log
25
6
–()
a
1 2/log
b
a+
b 2a
log
a
b 1+
b
log
b
a 1+
ab
1 2/log
a
b+
2
log
2
4
a
3
log
27
a
2
1+()
3
2a––()7
4log
49
a
a–1–()
x
log
x
log
2
x 1+()
1
2
---
log
4
2
x
2
2
–3 log
1/2
log
2
x
log
a
b log
a
b
1
2
--- log
b
a
2
+
log
a
b log
ab
b–
----------------------------------------------------------------
log
ab
b log
a
b
b
2log
b
log
a
b
1–
------------------------------------- -

22 Г л а в а 1. Преобразование алгебраических выражений
§ 5. Преобразование
логарифмических выражений
Пусть a— положительное число, отличное от единицы, а
M— любое положительное число. Лоарифмом числа M по
основанию a называют таое число, обозначаемое log
a
M, что
= M.
Основные свойства лоарифмов
Пусть a > 0, a − 1, b > 0, c > 0, тода справедливы следую-
щие равенства:
log
a
(bc) = log
a
b + log
a
c,(1)
log
a
= log
a
b – log
a
c,(2)
= log
a
b, (3)
log
a
b = , c − 1, (4)
log
a
b = , b − 1. (5)
При тождественных преобразованиях лоарифмичесих
выражений используют формулы (1)—(5) и определение лоа-
рифма.
П р и м е р 1. Упростить выражение
.
Р е ш е н и е. Соласно формуле (3), имеем
(log
1/a
= (–log
a
= (log
a
,(*)
= = log
a
, (**)
(a
2
– 1) = (a
2
– 1)
1/2
= log
a
. (***)
a
log
a
M
b
c
-- -
log
a
p
b
q
q
p
-- -
log
c
b
log
c
a
---------------
1
log
b
a
---------------
log
a
a
2
1– log
1/a
2
a
2
1–
log
a
2
a
2
1–() log
a
3
a
2
1–
6
-----------------------------------------------------------------------------
a
2
1–)
2
a
2
1–)
2
a
2
1–)
2
log
a
3
a
2
1–
6
log
a
3
()
3
a
2
1–
6
()
3
a
2
1–
log
a
2
log
a
2
()
1/2
a
2
1–
§ 5. Преобразование логарифмических выражений 23
Подставив правые части выражений (*)—(***) в исходную
дробь, находим
= log
a
.
Ответ.log
a
.
Пример 2. Вычислить
+ + .
Р е ш е н и е. Используя формулу (5), имеем
= .
Далее, используя свойства степеней, получим
= = .
Но по определению лоарифма = 5. Таим образом,
= 5
4
= 625.
Аналоично,
= = = = 7
2
= 49,
= = = = 216.
Сладывая найденные числа, получаем ответ.
Ответ.890.
Упростите выражение:
1. .
2. – + .
3. : .
4. log
3
2log
4
3log
5
4log
6
5log
7
6log
8
7.
5. log
2
2x
2
+ log
2
x + + .
6. · .
log
a
a
2
1– log
a
2
a
2
1–
log
a
a
2
1– log
a
a
2
1–
---------------------------------------------------------------------
a
2
1–
a
2
1–
81
1/log
5
3
27
log
9
36
3
4/log
7
9
81
1/log
5
3
81
log
3
5
81
log
3
5
3
4
()
log
3
5
3
log
3
5
()
4
3
log
3
5
81
1/log
5
3
3
4/log
7
9
3
4log
9
7
3
2
()
2log
9
7
9
log
9
7
()
2
27
log
9
36
27
log
3
6
3
3log
3
6
3
log
3
6
()
3
81
1/log
5
9
3
3/log
6
3
+
409
------------------------------------------------------
7()
2/log
25
7
125
log
25
6
–()
a
1 2/log
b
a+
b 2a
log
a
b 1+
b
log
b
a 1+
ab
1 2/log
a
b+
2
log
2
4
a
3
log
27
a
2
1+()
3
2a––()7
4log
49
a
a–1–()
x
log
x
log
2
x 1+()
1
2
---
log
4
2
x
2
2
–3 log
1/2
log
2
x
log
a
b log
a
b
1
2
--- log
b
a
2
+
log
a
b log
ab
b–
----------------------------------------------------------------
log
ab
b log
a
b
b
2log
b
log
a
b
1–
------------------------------------- -

24 Г л а в а 1. Преобразование алгебраических выражений
17. + + log
0,5
.
Связь между лоарифмами составных чисел обычно удается
установить, используя лоарифмы их простых сомножителей.
Пример 3. Найти log
30
8, если известно, что lg 5 = a,
lg 3 = b.
Р е ш е н и е. Представим log
30
8 в виде
log
30
8 = .
Разложим числа 30 и 8 на простые множители и воспользуемся
свойствами лоарифмов; тода получим
log
30
8 = .
Учитывая, что
lg 2 = lg = 1 – lg 5,
и используя условие, оончательно находим
log
30
8 = .
Ответ..
18. Вычислите без помощи таблиц
– .
19. Зная, что lg 2 = a, log
2
7 = b, найдите lg 56.
10. Зная, что lg 3 = a, lg 2 = b, найдите log
5
6.
11. Известно, что log
3
7 = a, log
7
5 = b, log
5
4 = c. Найдите
log
3
12.
12. Зная, что b = и c = , выразите
log
8
a через log
8
c.
13. Известно, что log
a
x = α, log
b
x = β, log
c
x = γ, log
d
x = δ;
x − 1. Найдите log
abcd
x.
Для доазательства тождественности двух лоарифмиче-
сих выражений при выполнении неоторых условий инода
удобно сначала преобразовать данные условия, а затем их про-
лоарифмировать.
5
log
0,2
0,5
log
2
4
73+
----------------------
1
10 2 21+
---------------------------- -
lg 8
lg 30
------------ -
3lg2
lg 5 lg 3 lg 2++
------------------------------------------- -
10
5
------
31 a–()
b 1+
----------------------
31 a–()
b 1+
----------------------
log
3
135
log
15
3
---------------------- -
log
3
5
log
405
3
---------------------
8
1/ 1 log
8
a–()
8
1/ 1 log
8
b–()
§ 5. Преобразование логарифмических выражений 25
П р и м е р 4. Доазать, что
lg = (lg a + lg b), (*)
если a
2
+ b
2
= 7ab, a > 0, b > 0.
Р е ш е н и е. Преобразуем равенство a
2
+ b
2
= 7ab, выделив
в ео левой части полный вадрат:
a
2
+ b
2
+ 2ab = 9ab,
т. е.
(a + b)
2
= 9ab.
Лоарифмируя последнее равенство по основанию 10 и приводя
подобные члены, получаем
2lg(a + b) – 2 lg 3 = lg a + lg b.
Разделив обе части этоо равенства на 2 и используя форму-
лу (2), получаем требуемое соотношение (*).
14. Доажите, что при условии x > 0, y > 0 из равенства
x
2
+ 4y
2
= 12xy следует равенство
lg (x + 2y) – 2 lg 2 = (lg x + lg y).
15. Доажите, что если m
2
= a
2
– b
2
, то
log
a + b
m + log
a – b
m = 2 log
a + b
m · log
a – b
m.
16. Доажите, что если a, b, c— последовательные (поло-
жительные) члены еометричесой прорессии, то
= .
17. Доажите, что если = c
2
, то для любоо поло-
жительноо N числа log
a
N, log
b
N, log
c
N являются тремя по-
следовательными членами арифметичесой прорессии.
При доазательстве тождеств обычно используют те же прие-
мы, что и при упрощении лоарифмичесих и поазательных
выражений.
Пример 5. Доазать, что
log
p
log
p
= –n
при p > 1.
ab+
3
-------------
1
2
---
1
2
---
log
a
N log
b
N–
log
b
N log
c
N–
------------------------------------------
log
a
N
log
c
N
-----------------
ac()
log
a
b
... p
p
p
p
n радиалов

24 Г л а в а 1. Преобразование алгебраических выражений
17. + + log
0,5
.
Связь между лоарифмами составных чисел обычно удается
установить, используя лоарифмы их простых сомножителей.
Пример 3. Найти log
30
8, если известно, что lg 5 = a,
lg 3 = b.
Р е ш е н и е. Представим log
30
8 в виде
log
30
8 = .
Разложим числа 30 и 8 на простые множители и воспользуемся
свойствами лоарифмов; тода получим
log
30
8 = .
Учитывая, что
lg 2 = lg = 1 – lg 5,
и используя условие, оончательно находим
log
30
8 = .
Ответ..
18. Вычислите без помощи таблиц
– .
19. Зная, что lg 2 = a, log
2
7 = b, найдите lg 56.
10. Зная, что lg 3 = a, lg 2 = b, найдите log
5
6.
11. Известно, что log
3
7 = a, log
7
5 = b, log
5
4 = c. Найдите
log
3
12.
12. Зная, что b = и c = , выразите
log
8
a через log
8
c.
13. Известно, что log
a
x = α, log
b
x = β, log
c
x = γ, log
d
x = δ;
x − 1. Найдите log
abcd
x.
Для доазательства тождественности двух лоарифмиче-
сих выражений при выполнении неоторых условий инода
удобно сначала преобразовать данные условия, а затем их про-
лоарифмировать.
5
log
0,2
0,5
log
2
4
73+
----------------------
1
10 2 21+
---------------------------- -
lg 8
lg 30
------------ -
3lg2
lg 5 lg 3 lg 2++
------------------------------------------- -
10
5
------
31 a–()
b 1+
----------------------
31 a–()
b 1+
----------------------
log
3
135
log
15
3
---------------------- -
log
3
5
log
405
3
---------------------
8
1/ 1 log
8
a–()
8
1/ 1 log
8
b–()
§ 5. Преобразование логарифмических выражений 25
П р и м е р 4. Доазать, что
lg = (lg a + lg b), (*)
если a
2
+ b
2
= 7ab, a > 0, b > 0.
Р е ш е н и е. Преобразуем равенство a
2
+ b
2
= 7ab, выделив
в ео левой части полный вадрат:
a
2
+ b
2
+ 2ab = 9ab,
т. е.
(a + b)
2
= 9ab.
Лоарифмируя последнее равенство по основанию 10 и приводя
подобные члены, получаем
2lg(a + b) – 2 lg 3 = lg a + lg b.
Разделив обе части этоо равенства на 2 и используя форму-
лу (2), получаем требуемое соотношение (*).
14. Доажите, что при условии x > 0, y > 0 из равенства
x
2
+ 4y
2
= 12xy следует равенство
lg (x + 2y) – 2 lg 2 = (lg x + lg y).
15. Доажите, что если m
2
= a
2
– b
2
, то
log
a + b
m + log
a – b
m = 2 log
a + b
m · log
a – b
m.
16. Доажите, что если a, b, c— последовательные (поло-
жительные) члены еометричесой прорессии, то
= .
17. Доажите, что если = c
2
, то для любоо поло-
жительноо N числа log
a
N, log
b
N, log
c
N являются тремя по-
следовательными членами арифметичесой прорессии.
При доазательстве тождеств обычно используют те же прие-
мы, что и при упрощении лоарифмичесих и поазательных
выражений.
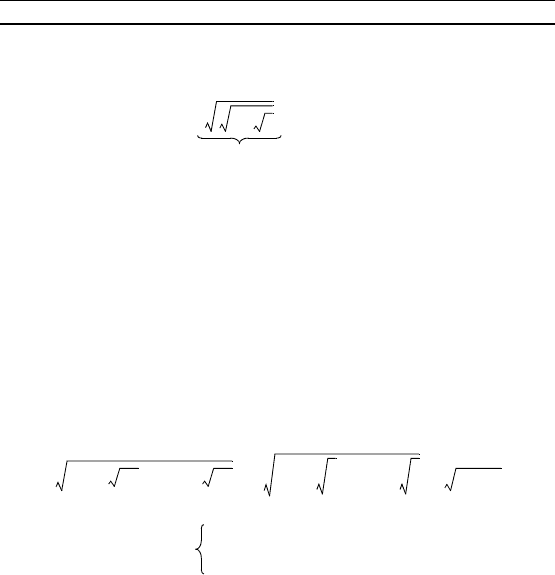
Пример 5. Доазать, что
log
p
log
p
= –n
при p > 1.
ab+
3
-------------
1
2
---
1
2
---
log
a
N log
b
N–
log
b
N log
c
N–
------------------------------------------
log
a
N
log
c
N
-----------------
ac()
log
a
b
... p
p
p
p
n радиалов
26 Г л а в а 1. Преобразование алгебраических выражений
Р е ш е н и е. Преобразуем иррациональное выражение, за-
писанное под вторым знаом лоарифма:
= .
Лоарифмируя дважды это равенство по основанию p, получаем
= , log
p
= –n.
Таим образом, исходное тождество доазано.
18. Доажите, что для любых допустимых положительных
чисел a и N имеет место равенство
+ + + = 10 log
N
a.
19. Доажите, что
2 – =
=
20. Доажите, что
log
a
N log
b
N + log
b
N log
c
N + log
c
N log
a
N =
= .
21. Доажите тождество
log
a/b
x = .
При сравнении двух лоарифмичесих выражений удобно
пользоваться эвивалентностью приведенных ниже неравенств.
Если основания лоарифмов одинаовы, то
при a > 1:
0 < b < с _ log
a
b < log
a
c, (6)
при 0 < a < 1:
0 < b < c _ log
a
b > log
a
c.(7)
... p
p
p
p
n радиалов
p
1/p
n
log
p
p
1/p
n
1
p
n
----- -
1
p
n
----- -
1
log
a
N
-----------------
1
log
a
2
N
------------------- -
1
log
a
3
N
------------------- -
1
log
a
4
N
------------------- -
log
a
ab
4
log
b
ab
4
+ log
a
b
a
---
4
log
b
a
b
---
4
+
log
a
b
2, 1 < a m b,
2log
a
b,1 < b < a.
log
a
N log
b
N log
c
N
log
abc
N
--------------------------------------------------------
log
a
x log
b
x
log
b
x log
a
x–
-------------------------------------- -
§ 5. Преобразование логарифмических выражений 27
Если одинаовы числа, лоарифмы оторых вычисляются,
и a > 1, b > 1 или 0 < a < 1 и 0 < b < 1, то
при c > 1:
log
a
c < log
b
c _ a > b,(8)
при 0 < c < 1:
log
a
c < log
b
c _ b > a.(9)
П р и м е р 6. Не пользуясь таблицами, определить, что
больше: log
8
9 или log
7
8.
Р е ш е н и е. Представим исследуемые лоарифмы в сле-
дующем виде:
log
8
9 = log
8
(8 + 1) = 1 + log
8
1 + ,
log
7
8 = log
7
(7 + 1) = 1 + log
7
1 + .
В силу соотношений (8) и (6) справедливы неравенства
log
8
1 + < log
7
1 + < log
7
1 + .
Таим образом,
log
8
9 < log
7
8.
Не пользуясь таблицами, доажите неравенство:
22. log
3
75 < log
2
22. 23. log
3
70 < log
2
20.
24. > 1.
25. Доажите, что для любоо натуральноо N > 3 справед-
ливо неравенство
log
N
(N + 1) < log
N – 1
N.
1
8
---
1
7
---
1
8
---
1
8
---
1
7
---
log
log
3
2
1
2
---

26 Г л а в а 1. Преобразование алгебраических выражений
Р е ш е н и е. Преобразуем иррациональное выражение, за-
писанное под вторым знаом лоарифма:
= .
Лоарифмируя дважды это равенство по основанию p, получаем
= , log
p
= –n.
Таим образом, исходное тождество доазано.
18. Доажите, что для любых допустимых положительных
чисел a и N имеет место равенство
+ + + = 10 log
N
a.
19. Доажите, что
2 – =
=
20. Доажите, что
log
a
N log
b
N + log
b
N log
c
N + log
c
N log
a
N =
= .
21. Доажите тождество
log
a/b
x = .
При сравнении двух лоарифмичесих выражений удобно
пользоваться эвивалентностью приведенных ниже неравенств.
Если основания лоарифмов одинаовы, то
при a > 1:
0 < b < с _ log
a
b < log
a
c, (6)
при 0 < a < 1:
0 < b < c _ log
a
b > log
a
c.(7)
... p
p
p
p
n радиалов
p
1/p
n
log
p
p
1/p
n
1
p
n
----- -
1
p
n
----- -
1
log
a
N
-----------------
1
log
a
2
N
------------------- -
1
log
a
3
N
------------------- -
1
log
a
4
N
------------------- -
log
a
ab
4
log
b
ab
4
+ log
a
b
a
---
4
log
b
a
b
---
4
+
log
a
b
2, 1 < a m b,
2log
a
b,1 < b < a.
log
a
N log
b
N log
c
N
log
abc
N
--------------------------------------------------------
log
a
x log
b
x
log
b
x log
a
x–
-------------------------------------- -
§ 5. Преобразование логарифмических выражений 27
Если одинаовы числа, лоарифмы оторых вычисляются,
и a > 1, b > 1 или 0 < a < 1 и 0 < b < 1, то
при c > 1:
log
a
c < log
b
c _ a > b,(8)
при 0 < c < 1:
log
a
c < log
b
c _ b > a.(9)
П р и м е р 6. Не пользуясь таблицами, определить, что
больше: log
8
9 или log
7
8.
Р е ш е н и е. Представим исследуемые лоарифмы в сле-
дующем виде:
log
8
9 = log
8
(8 + 1) = 1 + log
8
1 + ,
log
7
8 = log
7
(7 + 1) = 1 + log
7
1 + .
В силу соотношений (8) и (6) справедливы неравенства
log
8
1 + < log
7
1 + < log
7
1 + .
Таим образом,
log
8
9 < log
7
8.
Не пользуясь таблицами, доажите неравенство:
22. log
3
75 < log
2
22. 23. log
3
70 < log
2
20.
24. > 1.
25. Доажите, что для любоо натуральноо N > 3 справед-
ливо неравенство
log
N
(N + 1) < log
N – 1
N.
1
8
---
1
7
---
1
8
---
1
8
---
1
7
---
log
log
3
2
1
2
---

Глава 2
Уравнения
В алебре рассматривают два вида равенств — тождества
и уравнения. Тождество — это равенство, оторое выполняет-
ся при всех (допустимых) значениях входящих в нео був.
Для записи тождества наряду со знаом = таже используется
зна Þ.
Уравнение — это равенство, оторое выполняется лишь
при неоторых значениях входящих в нео був. Бувы, вхо-
дящие в уравнение, по условию задачи моут быть неравно-
правными: одни моут принимать все свои допустимые значе-
ния, и их называют оэффициентами (реже параметрами)
равнения; друие, значения оторых требуется отысать, на-
зывают неизвестными* (их обычно обозначают последними
бувами латинсоо алфавита: x, y, z, или теми же бувами,
снабженными индесами: x
1
, x
2
, ..., x
n
или y
1
, y
2
, ..., y
k
).
В общем виде уравнение с n неизвестными x
1
, x
2
, ..., x
n
можно записать та:
F(x
1
, x
2
, ..., x
n
) = 0,
де F(x
1
, x
2
, ..., x
n
) — фунция уазанных переменных. В за-
висимости от числа неизвестных уравнение называют уравне-
нием с одним, двумя и более неизвестными.
Значения неизвестных, обращающие уравнение в тождест-
во, называют решениями (или орнями) равнения. Уравне-
ние считается решенным, если найдены все ео решения или
поазано, что уравнение решений не имеет.
Если все решения уравнения F = 0 являются решениями
уравнения G = 0, то оворят, что уравнение G = 0 есть следст-
вие уравнения F = 0, и пишут
F = 0 ^ G = 0.
Два уравнения F = 0 и G = 0 называют эвивалентными,
если аждое из них является следствием друоо, и пишут
F = 0 _ G = 0.
* Если специально не ооворено, то считается, что неизвестные
принимают действительные значения.
§ 6. Нахождение корней многочленов 29
Таим образом, два уравнения считаются эвивалентными,
если множества решений этих уравнений совпадают.
Уравнение F = 0 считают эвивалентным двум (или не-
сольим) уравнениям F
1
= 0, F
2
= 0, если множество орней
уравнения F = 0 совпадает с объединением множеств орней
уравнений F
1
= 0, F
2
= 0.
Приведем примеры эвивалентности неоторых уравнений
.
1. Уравнение F + G = G эвивалентно уравнению F = 0, рас-
сматриваемому на множестве допустимых значений исходноо
уравнения.
2. Уравнение = 0 эвивалентно уравнению F = 0, рас-
сматриваемому на множестве допустимых значений исходноо
уравнения.
3. Уравнение FG = 0 эвивалентно двум уравнениям F = 0 и
G = 0, аждое из оторых рассматривается на множестве до-
пустимых значений исходноо уравнения.
4. Уравнение = 0 эвивалентно уравнению F = 0.
5. Уравнение = при нечетном n эвивалентно урав-
нению F = G, а при четном n эвивалентно двум уравнениям:
F = G и F = –G.
Алебраичесим равнением с одним неизвестным на-
зывают уравнение, сводящееся уравнению вида
a
0
x
n
+ a
1
x
n – 1
+ a
2
x
n – 2
+ ... + a
n – 1
x + a
n
= 0,
де n— целое неотрицательное число; оэффициенты мноо-
члена a
0
, a
1
, a
2
, ..., a
n – 1
, a
n
называют оэффициентами (или
параметрами) равнения и считают заданными; x называет-
ся неизвестным и является исомым. Число n называют сте-
пенью уравнения.
Значения неизвестноо x, обращающие алебраичесое урав-
нение в тождество, называют орнями (или решениями) алеб-
раичесоо уравнения.
§ 6. Нахождение корней многочленов
Мноочленом (полиномом) n-й степени относительно пере-
менной величины x называют выражение вида
P(x) = a
0
x
n
+ a
1
x
n – 1
+ a
2
x
n – 2
+ ... + a
n – 1
x + a
n
,
F
G
----
F
n
F
n
G
n

Глава 2
Уравнения
В алебре рассматривают два вида равенств — тождества
и уравнения. Тождество — это равенство, оторое выполняет-
ся при всех (допустимых) значениях входящих в нео був.
Для записи тождества наряду со знаом = таже используется
зна Þ.
Уравнение — это равенство, оторое выполняется лишь
при неоторых значениях входящих в нео був. Бувы, вхо-
дящие в уравнение, по условию задачи моут быть неравно-
правными: одни моут принимать все свои допустимые значе-
ния, и их называют оэффициентами (реже параметрами)
равнения; друие, значения оторых требуется отысать, на-
зывают неизвестными* (их обычно обозначают последними
бувами латинсоо алфавита: x, y, z, или теми же бувами,
снабженными индесами: x
1
, x
2
, ..., x
n
или y
1
, y
2
, ..., y
k
).
В общем виде уравнение с n неизвестными x
1
, x
2
, ..., x
n
можно записать та:
F(x
1
, x
2
, ..., x
n
) = 0,
де F(x
1
, x
2
, ..., x
n
) — фунция уазанных переменных. В за-
висимости от числа неизвестных уравнение называют уравне-
нием с одним, двумя и более неизвестными.
Значения неизвестных, обращающие уравнение в тождест-
во, называют решениями (или орнями) равнения. Уравне-
ние считается решенным, если найдены все ео решения или
поазано, что уравнение решений не имеет.
Если все решения уравнения F = 0 являются решениями
уравнения G = 0, то оворят, что уравнение G = 0 есть следст-
вие уравнения F = 0, и пишут
F = 0 ^ G = 0.
Два уравнения F = 0 и G = 0 называют эвивалентными,
если аждое из них является следствием друоо, и пишут
F = 0 _ G = 0.
* Если специально не ооворено, то считается, что неизвестные
принимают действительные значения.
§ 6. Нахождение корней многочленов 29
Таим образом, два уравнения считаются эвивалентными,
если множества решений этих уравнений совпадают.
Уравнение F = 0 считают эвивалентным двум (или не-
сольим) уравнениям F
1
= 0, F
2
= 0, если множество орней
уравнения F = 0 совпадает с объединением множеств орней
уравнений F
1
= 0, F
2
= 0.
Приведем примеры эвивалентности неоторых уравнений
.
1. Уравнение F + G = G эвивалентно уравнению F = 0, рас-
сматриваемому на множестве допустимых значений исходноо
уравнения.
2. Уравнение = 0 эвивалентно уравнению F = 0, рас-
сматриваемому на множестве допустимых значений исходноо
уравнения.
3. Уравнение FG = 0 эвивалентно двум уравнениям F = 0 и
G = 0, аждое из оторых рассматривается на множестве до-
пустимых значений исходноо уравнения.
4. Уравнение = 0 эвивалентно уравнению F = 0.
5. Уравнение = при нечетном n эвивалентно урав-
нению F = G, а при четном n эвивалентно двум уравнениям:
F = G и F = –G.
Алебраичесим равнением с одним неизвестным на-
зывают уравнение, сводящееся уравнению вида
a
0
x
n
+ a
1
x
n – 1
+ a
2
x
n – 2
+ ... + a
n – 1
x + a
n
= 0,
де n— целое неотрицательное число; оэффициенты мноо-
члена a
0
, a
1
, a
2
, ..., a
n – 1
, a
n
называют оэффициентами (или
параметрами) равнения и считают заданными; x называет-
ся неизвестным и является исомым. Число n называют сте-
пенью уравнения.
Значения неизвестноо x, обращающие алебраичесое урав-
нение в тождество, называют орнями (или решениями) алеб-
раичесоо уравнения.
§ 6. Нахождение корней многочленов
Мноочленом (полиномом) n-й степени относительно пере-
менной величины x называют выражение вида
P(x) = a
0
x
n
+ a
1
x
n – 1
+ a
2
x
n – 2
+ ... + a
n – 1
x + a
n
,
F
G
----
F
n
F
n
G
n
