Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.

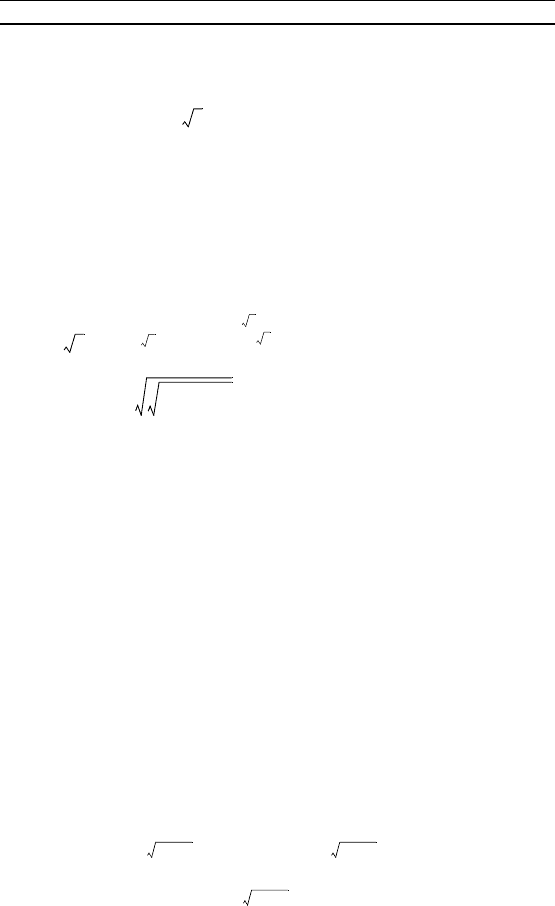
50 Г л а в а 2. Уравнения
15. 3 · + · = 6 · – ·
16. = .
17. 4 · = 5 · – 7 · = 40.
18. 5 + 4 · = .
19. = 512 ·
10. 5
|4x – 6|
= 25
3x – 4
.
11. · · = 81.
12. · = 1.
13. · = .
14. · = .
15. Найдите решение уравнения = , удовлетворяю-
щее условию x > –3.
Сведение заменой переменных алебраичесом равне-
нию. Пусть поазательное уравнение имеет вид
g(a
f(x)
) = 0, (3)
де f(x) — неоторая фунция от x. Тода заменой y = a
f(x)
оно
сводится уравнениям вида
a
f(x)
= y
i
,
де y
i
— орни уравнения g(y) = 0.
П р и м е р 2. Решить уравнение
– 5 · = 6.
Р е ш е н и е. Полаая = y, получаем вадратное
уравнение
y
2
– y – 6 = 0,
4
x
1
3
---
9
x 2+
4
x 1+
1
2
---
9
x 1+
.
7
2x
2
5x–9–
2
----------------------------------
2()
3log
2
7
3
x 2+
3
x
3
x 1+
1
25
------
sin x
5
cos 2x
25
0,5 sin 2x
16
x 5+
x 7–
--------------
64
x 17+
x 3–
------- ----------
.
3
3
x
1 x+
------------------
1
3
---
2 xx++
21 x+()
---------------------------- -
8
x 3–
3x 7–
-----------------
0,25
3x 1–
x 1–
-----------------
3
0,6
x
25
9
------
x
2
12–
27
125
----------
3
(2,4)
1 xsin–
[0,41(6)]
xsin 0,5+
12
5
------
0,5
3
x
2
4x+
1
25
------
4
x
2
2– x+
2
x 1– x
2
2–+
2
x
2
2– x+
5
2
---
§ 10. Показательные уравнения 51
орнями отороо являются y
1
= 4 и y
2
= –1,5. Таим образом,
решение данноо уравнения сводится решению уравнений
= 4, = –1,5.
Второе уравнение не имеет решений, та а > 0 при
всех допустимых значениях x. Из первоо уравнения следует,
что
x + = 2.
Уединяя радиал и возводя обе части уравнения в вадрат,
имеем
x
2
– 2 = 4 – 4x + x
2
.
Приводя подобные члены, находим единственный орень x = 1,5.
Проверой убеждаемся, что этот орень удовлетворяет исход-
ному уравнению.
Ответ. x = 1,5.
Решите уравнение:
16. – 36 · + 3 = 0.
17. 3 – 10 + 3 = 0.
18. – + + = 6.
19. – + 12 = 0.
20. – 6 · + = 0.
21. + 2 = 9 · .
Поазательные уравнения, основания степеней оторых яв-
ляются последовательными членами еометричесой прорес-
сии, а поазали степеней одинаовы, приводятся уравнениям
вида (3) делением на любой из райних членов.
Пример 3. Решить уравнение
6 · – 13 · + 6 · = 0.
Р е ш е н и е. Разделим обе части уравнения на :
6 – 13 + 6 = 0.
2
xx
2
2–+
2
xx
2
2–+
2
xx
2
2–+
x
2
2–
9
x
2
1–
3
x
2
3–
81
x
9
x
3
1 x–
3
1 x+
9
x
9
–x
64
1
x
---
2
2
3
x
-- -
+
4
log
9
x
2
log
9
x
2
log
3
27
4
3x
2
2x–1+
2
3x
2
2x–
4
x
6
x
9
x
9
x
4
9
---
x
6
9
---
x
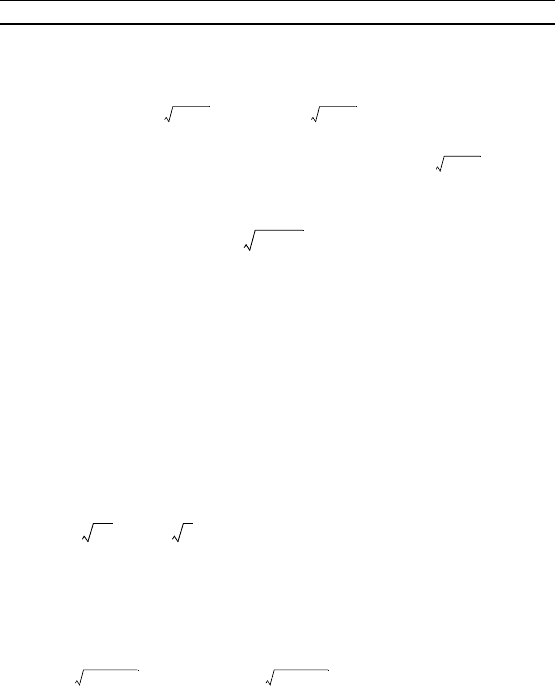
50 Г л а в а 2. Уравнения
15. 3 · + · = 6 · – ·
16. = .
17. 4 · = 5 · – 7 · = 40.
18. 5 + 4 · = .
19. = 512 ·
10. 5
|4x – 6|
= 25
3x – 4
.
11. · · = 81.
12. · = 1.
13. · = .
14. · = .
15. Найдите решение уравнения = , удовлетворяю-
щее условию x > –3.
Сведение заменой переменных алебраичесом равне-
нию. Пусть поазательное уравнение имеет вид
g(a
f(x)
) = 0, (3)
де f(x) — неоторая фунция от x. Тода заменой y = a
f(x)
оно
сводится уравнениям вида
a
f(x)
= y
i
,
де y
i
— орни уравнения g(y) = 0.
П р и м е р 2. Решить уравнение
– 5 · = 6.
Р е ш е н и е. Полаая = y, получаем вадратное
уравнение
y
2
– y – 6 = 0,
4
x
1
3
---
9
x 2+
4
x 1+
1
2
---
9
x 1+
.
7
2x
2
5x–9–
2
----------------------------------
2()
3log
2
7
3
x 2+
3
x
3
x 1+
1
25
------
sin x
5
cos 2x
25
0,5 sin 2x
16
x 5+
x 7–
--------------
64
x 17+
x 3–
------- ----------
.
3
3
x
1 x+
------------------
1
3
---
2 xx++
21 x+()
---------------------------- -
8
x 3–
3x 7–
-----------------
0,25
3x 1–
x 1–
-----------------
3
0,6
x
25
9
------
x
2
12–
27
125
----------
3
(2,4)
1 xsin–
[0,41(6)]
xsin 0,5+
12
5
------
0,5
3
x
2
4x+
1
25
------
4
x
2
2– x+
2
x 1– x
2
2–+
2
x
2
2– x+
5
2
---
§ 10. Показательные уравнения 51
орнями отороо являются y
1
= 4 и y
2
= –1,5. Таим образом,
решение данноо уравнения сводится решению уравнений
= 4, = –1,5.
Второе уравнение не имеет решений, та а > 0 при
всех допустимых значениях x. Из первоо уравнения следует,
что
x + = 2.
Уединяя радиал и возводя обе части уравнения в вадрат,
имеем
x
2
– 2 = 4 – 4x + x
2
.
Приводя подобные члены, находим единственный орень x = 1,5.
Проверой убеждаемся, что этот орень удовлетворяет исход-
ному уравнению.
Ответ. x = 1,5.
Решите уравнение:
16. – 36 · + 3 = 0.
17. 3 – 10 + 3 = 0.
18. – + + = 6.
19. – + 12 = 0.
20. – 6 · + = 0.
21. + 2 = 9 · .
Поазательные уравнения, основания степеней оторых яв-
ляются последовательными членами еометричесой прорес-
сии, а поазали степеней одинаовы, приводятся уравнениям
вида (3) делением на любой из райних членов.
Пример 3. Решить уравнение
6 · – 13 · + 6 · = 0.
Р е ш е н и е. Разделим обе части уравнения на :
6 – 13 + 6 = 0.
2
xx
2
2–+
2
xx
2
2–+
2
xx
2
2–+
x
2
2–
9
x
2
1–
3
x
2
3–
81
x
9
x
3
1 x–
3
1 x+
9
x
9
–x
64
1
x
---
2
2
3
x
-- -
+
4
log
9
x
2
log
9
x
2
log
3
27
4
3x
2
2x–1+
2
3x
2
2x–
4
x
6
x
9
x
9
x
4
9
---
x
6
9
---
x
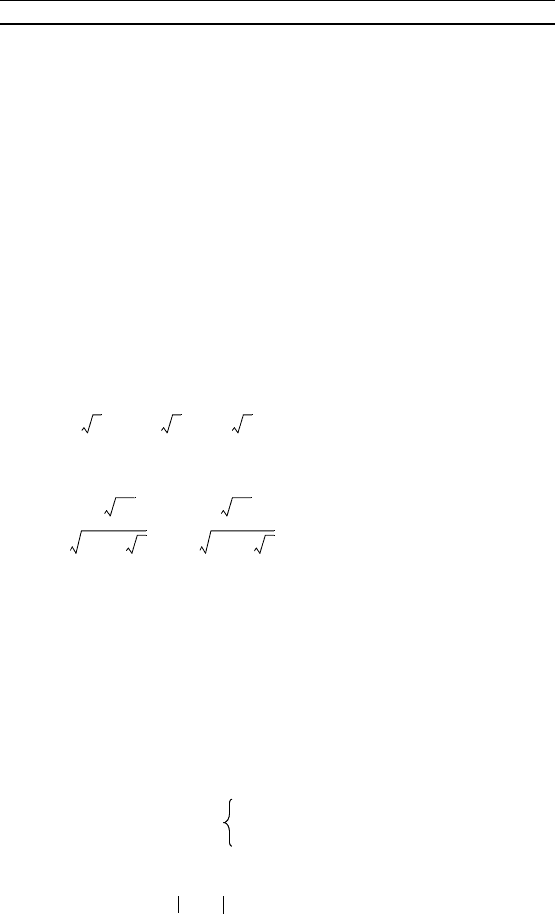
52 Г л а в а 2. Уравнения
Полаая = y, получаем уравнение
6y
2
– 13y + 6 = 0,
орнями отороо являются y
1
= и y
2
= . Таим образом,
решение уравнения сводится решению двух простейших по-
азательных уравнений = и = .
Ответ. x
1
= 1, x
2
= –1.
Решите уравнение:
22. 7 · – 9 · + 2 · = 0.
23. 3 · + = 2 · . 24. 8
x
+ 18
x
= 2 · 27
x
.
25. 6 – 13 + 6 = 0.
26. 16
x
– 5 · 8
x
+ 6 · 4
x
= 0.
27. 2
3x – 3
– 5 + 6 · 2
3 – 3x
= 0. 28. 27
x
+ 12
x
= 2 · 8
x
.
29. (4 + )
x
+ (4 – )
x
= 62.
30. ()
x
+ ( )
x
= 10.
31. 9
1/x
+ 12
1/x
= 16
1/x
. 32. – = 24.
33. 5
x – 1
+ 5 · 0,2
x – 2
= 26.
34. 10
2/x
+ 25
1/x
= 4,25 · 50
1/x
.
Уравнение вида
(a(x))
b(x)
= (a(x))
c(x)
эвивалентно уравнению
a(x) = 1
и системе
П р и м е р 4. Решить уравнение
= |x – 2|
3x
.
Р е ш е н и е. Исходное уравнение эвивалентно уравнению
|x – 2| = 1 (*)
2
3
---
x
3
2
---
2
3
---
3
2
---
x
3
2
---
3
2
---
x
2
3
---
4
x
2
14
x
2
49
x
2
16
x
36
x
81
x
9
x
6
x
4
x
15 15
526+ 526–
5
1 x
3
+
5
1 x
3
–
b(x) = c(x).
a(x) > 0.
x 2–
10x
2
1–
§ 10. Показательные уравнения 53
и системе
(**)
Уравнение (*) имеет орни x
1
= 3, x
2
= 1, а системе (**)
удовлетворяют значения x
3
= 0,5, x
4
= – 0,2.
Ответ. x
1
= 3, x
2
= 1, x
3
= 0,5, x
4
= – 0,2.
Решите уравнение:
35. = .
36. = 1. 37. = .
38. = 5. 39. = .
Неоторые специальные приемы решения поазательных
равнений. В ряде случае уравнения можно свести рассмот-
ренным выше, если преобразовать отдельные их элементы, ис-
пользуя основное лоарифмичесое тождество.
Пример 5. Решить уравнение
+ = 162.
Р е ш е н и е. Применяя основное лоарифмичесое тожде-
ство, преобразуем второе слааемое в левой части уравнения:
= = . (*)
Теперь подставим выражение (*) в исходное уравнение:
2 · = 162. (**)
Уравнение (**) эвивалентно уравнению = 4, оторое
в свою очередь эвивалентно двум уравнениям
log
3
x = 2, log
3
x = –2.
Решив их, получаем x
1
= 9, x
2
= .
Ответ. x
1
= 9, x
2
= .
Решите уравнение:
40. 5
lg x
= 50 – x
lg 5
. 41. + x
lg x
= 20.
42. – 5 · 2
lg x
+ 6 = 0.
10x
2
– 1 = 3x,
|x – 2| − 0.
x 3–
x 1+
4
x 3–
x 2–
x 3–
3x
2
10x–3+
x
log
a
x
(a
π
)
log
a
3
x
x()
log
5
x 1–
x
lg x 7+
10
4(lg x 1)+
3
log
3
2
x
x
log
3
x
x
log
3
x
3
log
3
x
()
log
3
x
3
log
3
2
x
3
log
3
2
x
log
3
2
x
1
9
---
1
9
---
10
lg
2
x
x
2lg2
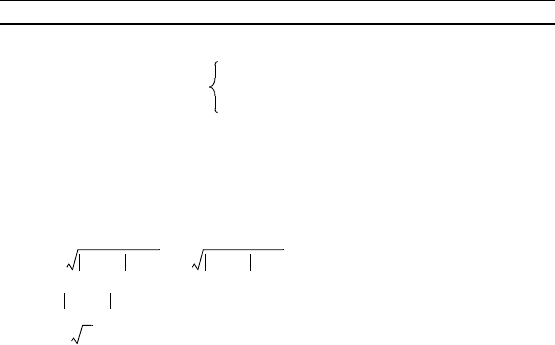
52 Г л а в а 2. Уравнения
Полаая = y, получаем уравнение
6y
2
– 13y + 6 = 0,
орнями отороо являются y
1
= и y
2
= . Таим образом,
решение уравнения сводится решению двух простейших по-
азательных уравнений = и = .
Ответ. x
1
= 1, x
2
= –1.
Решите уравнение:
22. 7 · – 9 · + 2 · = 0.
23. 3 · + = 2 · . 24. 8
x
+ 18
x
= 2 · 27
x
.
25. 6 – 13 + 6 = 0.
26. 16
x
– 5 · 8
x
+ 6 · 4
x
= 0.
27. 2
3x – 3
– 5 + 6 · 2
3 – 3x
= 0. 28. 27
x
+ 12
x
= 2 · 8
x
.
29. (4 + )
x
+ (4 – )
x
= 62.
30. ()
x
+ ( )
x
= 10.
31. 9
1/x
+ 12
1/x
= 16
1/x
. 32. – = 24.
33. 5
x – 1
+ 5 · 0,2
x – 2
= 26.
34. 10
2/x
+ 25
1/x
= 4,25 · 50
1/x
.
Уравнение вида
(a(x))
b(x)
= (a(x))
c(x)
эвивалентно уравнению
a(x) = 1
и системе
П р и м е р 4. Решить уравнение
= |x – 2|
3x
.
Р е ш е н и е. Исходное уравнение эвивалентно уравнению
|x – 2| = 1 (*)
2
3
---
x
3
2
---
2
3
---
3
2
---
x
3
2
---
3
2
---
x
2
3
---
4
x
2
14
x
2
49
x
2
16
x
36
x
81
x
9
x
6
x
4
x
15 15
526+ 526–
5
1 x
3
+
5
1 x
3
–
b(x) = c(x).
a(x) > 0.
x 2–
10x
2
1–
§ 10. Показательные уравнения 53
и системе
(**)
Уравнение (*) имеет орни x
1
= 3, x
2
= 1, а системе (**)
удовлетворяют значения x
3
= 0,5, x
4
= – 0,2.
Ответ. x
1
= 3, x
2
= 1, x
3
= 0,5, x
4
= – 0,2.
Решите уравнение:
35. = .
36. = 1. 37. = .
38. = 5. 39. = .
Неоторые специальные приемы решения поазательных
равнений. В ряде случае уравнения можно свести рассмот-
ренным выше, если преобразовать отдельные их элементы, ис-
пользуя основное лоарифмичесое тождество.
Пример 5. Решить уравнение
+ = 162.
Р е ш е н и е. Применяя основное лоарифмичесое тожде-
ство, преобразуем второе слааемое в левой части уравнения:
= = . (*)
Теперь подставим выражение (*) в исходное уравнение:
2 · = 162. (**)
Уравнение (**) эвивалентно уравнению = 4, оторое
в свою очередь эвивалентно двум уравнениям
log
3
x = 2, log
3
x = –2.
Решив их, получаем x
1
= 9, x
2
= .
Ответ. x
1
= 9, x
2
= .
Решите уравнение:
40. 5
lg x
= 50 – x
lg 5
. 41. + x
lg x
= 20.
42. – 5 · 2
lg x
+ 6 = 0.
10x
2
– 1 = 3x,
|x – 2| − 0.
x 3–
x 1+
4
x 3–
x 2–
x 3–
3x
2
10x–3+
x
log
a
x
(a
π
)
log
a
3
x
x()
log
5
x 1–
x
lg x 7+
10
4(lg x 1)+
3
log
3
2
x
x
log
3
x
x
log
3
x
3
log
3
x
()
log
3
x
3
log
3
2
x
3
log
3
2
x
log
3
2
x
1
9
---
1
9
---
10
lg
2
x
x
2lg2

54 Г л а в а 2. Уравнения
Инода уравнение, содержащее неизвестное в поазателе
степени, удается решить с помощью исследования фунций,
входящих в левую и правую части уравнения.
Пример 6. Решить уравнение
7
6 – x
= x + 2.
Решение. Корень x = 5 можно найти подбором. Друих
решений уравнение не имеет, та а фунция f(x) = 7
6 – x
мо-
нотонно убывает, а фунция g(x) = x + 2 монотонно возрастает,
и, следовательно, рафии этих фунций моут пересечься не
более, чем в одной точе.
Ответ. x = 5.
Решите уравнение:
43. + = .
44. + = 34. 45. = .
46. + (x – 1) = 6 – 2x.
47. (x + 1) + 4x · – 16 = 0.
48. x
2
– x + 1 = 2 · 2
x – 1
– 4
x – 1
.
49. + = . 50. + = .
51. = –2x
2
+ 6x –9.
§ 11. Логарифмические уравнения
Лоарифмичесим равнением называют уравнение, со-
держащее неизвестную величину под знаом лоарифма. Про-
стейшее лоарифмичесое уравнение
log
a
x = b, a > 0, a − 1, (1)
с множеством допустимых значений x > 0 имеет решение x = a
b
.
Лоарифмичесое уравнение, в отором под знаом лоа-
рифма находится неоторая фунция f(x):
log
a
f(x) = b, a > 0, a − 1, (2)
23+()
x
23–()
x
2
x
3
x 1–
5
x 1–
2
3x
2
2x
3
–
x
2
1+
x
---------------- -
4
x
2
x
9
x 3–
3
x 3–
5
x
12
x
13
x
3
x
2
4
x
2
5
x
2
4
3
---
x
§ 11. Логарифмические уравнения 55
имеет множество допустимых значений x, задаваемых неравен-
ством f(x) > 0, и эвивалентно уравнению
f(x) = a
b
.
Сведение простейшим лоарифмичесим равнениям. Не-
оторые лоарифмичесие уравнения решаются с использова-
нием основных свойств лоарифмов (1)—(5) (см. § 5), позво-
ляющих свести решение данноо уравнения решению про-
стейшео лоарифмичесоо уравнения.
П р и м е р 1. Решить уравнение
2 – x + 3 log
5
2 = log
5
( – ).
Р е ш е н и е. Перенесем лоарифм из левой части уравне-
ния в правую и, воспользовавшись свойствами лоарифмов, за-
пишем уравнение в виде
2 – x = log
5
.
Последнее уравнение эвивалентно уравнению
= ,
оторое можно записать в виде
= 9 · , или = , или = 1.
Полученное поазательное уравнение эвивалентно уравнению
x – 2 = 0, решение отороо есть x = 2.
Множество допустимых значений x для данноо уравнения
определяется неравенством
– > 0.
При x = 2 это неравенство справедливо, и, следовательно, x = 2
является решением исходноо лоарифмичесоо уравнения.
Ответ. x = 2.
Решите уравнение:
1. log
5
[2 + log
3
(3 + x)] = 0.
2. lg (5 – x) – lg (35 – x
3
) = 0.
3. log
3
( – 8) = 2 – x.
3
x
5
2 x–
3
x
5
2 x–
–
8
-------------------------- -
3
x
5
2 x–
–
8
-------------------------- -
5
2 x–
3
x
5
2 x–
3
x 2–
5
2 x–
15
x 2–
3
x
5
2 x–
1
3
---
3
x

54 Г л а в а 2. Уравнения
Инода уравнение, содержащее неизвестное в поазателе
степени, удается решить с помощью исследования фунций,
входящих в левую и правую части уравнения.
Пример 6. Решить уравнение
7
6 – x
= x + 2.
Решение. Корень x = 5 можно найти подбором. Друих
решений уравнение не имеет, та а фунция f(x) = 7
6 – x
мо-
нотонно убывает, а фунция g(x) = x + 2 монотонно возрастает,
и, следовательно, рафии этих фунций моут пересечься не
более, чем в одной точе.
Ответ. x = 5.
Решите уравнение:
43. + = .
44. + = 34. 45. = .
46. + (x – 1) = 6 – 2x.
47. (x + 1) + 4x · – 16 = 0.
48. x
2
– x + 1 = 2 · 2
x – 1
– 4
x – 1
.
49. + = . 50. + = .
51. = –2x
2
+ 6x –9.
§ 11. Логарифмические уравнения
Лоарифмичесим равнением называют уравнение, со-
держащее неизвестную величину под знаом лоарифма. Про-
стейшее лоарифмичесое уравнение
log
a
x = b, a > 0, a − 1, (1)
с множеством допустимых значений x > 0 имеет решение x = a
b
.
Лоарифмичесое уравнение, в отором под знаом лоа-
рифма находится неоторая фунция f(x):
log
a
f(x) = b, a > 0, a − 1, (2)
23+()
x
23–()
x
2
x
3
x 1–
5
x 1–
2
3x
2
2x
3
–
x
2
1+
x
---------------- -
4
x
2
x
9
x 3–
3
x 3–
5
x
12
x
13
x
3
x
2
4
x
2
5
x
2
4
3
---
x
§ 11. Логарифмические уравнения 55
имеет множество допустимых значений x, задаваемых неравен-
ством f(x) > 0, и эвивалентно уравнению
f(x) = a
b
.
Сведение простейшим лоарифмичесим равнениям. Не-
оторые лоарифмичесие уравнения решаются с использова-
нием основных свойств лоарифмов (1)—(5) (см. § 5), позво-
ляющих свести решение данноо уравнения решению про-
стейшео лоарифмичесоо уравнения.
П р и м е р 1. Решить уравнение
2 – x + 3 log
5
2 = log
5
( – ).
Р е ш е н и е. Перенесем лоарифм из левой части уравне-
ния в правую и, воспользовавшись свойствами лоарифмов, за-
пишем уравнение в виде
2 – x = log
5
.
Последнее уравнение эвивалентно уравнению
= ,
оторое можно записать в виде
= 9 · , или = , или = 1.
Полученное поазательное уравнение эвивалентно уравнению
x – 2 = 0, решение отороо есть x = 2.
Множество допустимых значений x для данноо уравнения
определяется неравенством
– > 0.
При x = 2 это неравенство справедливо, и, следовательно, x = 2
является решением исходноо лоарифмичесоо уравнения.
Ответ. x = 2.
Решите уравнение:
1. log
5
[2 + log
3
(3 + x)] = 0.
2. lg (5 – x) – lg (35 – x
3
) = 0.
3. log
3
( – 8) = 2 – x.
3
x
5
2 x–
3
x
5
2 x–
–
8
-------------------------- -
3
x
5
2 x–
–
8
-------------------------- -
5
2 x–
3
x
5
2 x–
3
x 2–
5
2 x–
15
x 2–
3
x
5
2 x–
1
3
---
3
x

56 Г л а в а 2. Уравнения
4. ( – 6) – ( – 2) = 2.
5. lg (3x
2
+ 12x + 19) – lg (3x + 4) = 1.
Лоарифмичесое уравнение вида
log
a (x)
f(x) = log
a (x)
g(x)
эвивалентно уравнению
f(x) = g (x),
рассматриваемому на множестве допустимых значений x, зада-
ваемом системой неравенств
f(x) > 0, g (x) > 0, a(x) > 0, a(x) − 1.
Если в данное уравнение входят лоарифмы по разным ос-
нованиям, то предварительно необходимо привести все лоа-
рифмы одному основанию.
П р и м е р 2. Решить уравнение
lg + lg (2x + 15) = 1. (*)
Р е ш е н и е. Множество допустимых значений неизвестно-
о x для данноо уравнения находится а решение системы
и представляет собой промежуто (1; +×). Используя свойства
лоарифмов, преобразуем уравнение (*) виду
lg ( · ) = 1.
Из последнео уравнения по определению лоарифма получаем
иррациональное уравнение
= 10,
имеющее решения x
1
= 5, x
2
= –11,5. Множеству допустимых
значений исходноо уравнения принадлежит лишь орень x
1
= 5,
оторый и является решением уравнения (*).
Ответ. x = 5.
Решите уравнение:
6. 2log
3
(x – 2) + log
3
(x – 4)
2
= 0.
7. log
5
= log
5
.
log
5
4
x
log
5
2
x
x 1–
1
2
---
x – 1 > 0,
2x + 15 > 0
x 1– 2x 15+
x 1–()2x 15+()
2 x+
10
------------- -
2
x 1+
------------- -
§ 11. Логарифмические уравнения 57
18. 0,5lg(x
2
– 10x + 25) + lg (x
2
– 6x + 3) =
= 2lg(x – 5) + 0,5 lg 25.
19. lg – lg x – lg = 0.
10. lg (x(x + 9)) + lg = 0.
11. log
2
(2x
2
– 2) = log
2
(5x – 4).
12. = 3.
13. log
x + 1
(x – 0,5) = log
x – 0,5
(x + 1).
14. (x
3
+ 3x
2
– 2x – 1) = log
2x
x + log
2x
2.
15. log
1 + x
(2x
3
+ 2x
2
– 3x + 1) = 3.
16. log
x + 1
(x
3
– 9x + 8) · log
x – 1
(x + 1) = 3.
17. log
x + 1
(x
2
+ x – 6)
2
= 4.
18. (9 – 16x
4
) = 2 + .
19. log
3x
+ = 1.
20. log
x
16 + log
2x
64 = 3.
21. 20 log
4x
+ 7 log
16x
x
3
– 3 log
x/2
x
2
= 0.
22. log
x
2 – log
4
x + = 0.
23. 2 – (1 + x) = 3 log
b
– (x
2
– 1)
2
.
24. 3log
x
4 + 2 log
4x
4 + 3 log
16x
4 = 0.
Сведение заменой переменных алебраичесом равне-
нию. Пусть лоарифмичесое уравнение имеет вид
f(log
a
x) = 0,
де f(x) — неоторая фунция от x. Тода заменой y = log
a
x
оно сводится уравнениям вида (1):
log
a
x = y
i
,
де y
i
— орни уравнения f(y) = 0.
Пример 3. Решить уравнение
(log
2
x)
2
– 5 log
2
x + 6 = 0.
1
10
------
x
2
4x–4+
3
1
2
---
1
x
-------
x 9+
x
------------- -
lg 35 x
3
–()
lg 5 x–()
-------------------------------
log
x
3
2x
2
3x–5++
log
34x
2
–
1
log
2
34x
2
–()
------------------------------------- -
3
x
---
log
3
2
x
x
7
6
---
log
b
2
x 1– log
b
4

56 Г л а в а 2. Уравнения
4. ( – 6) – ( – 2) = 2.
5. lg (3x
2
+ 12x + 19) – lg (3x + 4) = 1.
Лоарифмичесое уравнение вида
log
a (x)
f(x) = log
a (x)
g(x)
эвивалентно уравнению
f(x) = g (x),
рассматриваемому на множестве допустимых значений x, зада-
ваемом системой неравенств
f(x) > 0, g (x) > 0, a(x) > 0, a(x) − 1.
Если в данное уравнение входят лоарифмы по разным ос-
нованиям, то предварительно необходимо привести все лоа-
рифмы одному основанию.
П р и м е р 2. Решить уравнение
lg + lg (2x + 15) = 1. (*)
Р е ш е н и е. Множество допустимых значений неизвестно-
о x для данноо уравнения находится а решение системы
и представляет собой промежуто (1; +×). Используя свойства
лоарифмов, преобразуем уравнение (*) виду
lg ( · ) = 1.
Из последнео уравнения по определению лоарифма получаем
иррациональное уравнение
= 10,
имеющее решения x
1
= 5, x
2
= –11,5. Множеству допустимых
значений исходноо уравнения принадлежит лишь орень x
1
= 5,
оторый и является решением уравнения (*).
Ответ. x = 5.
Решите уравнение:
6. 2log
3
(x – 2) + log
3
(x – 4)
2
= 0.
7. log
5
= log
5
.
log
5
4
x
log
5
2
x
x 1–
1
2
---
x – 1 > 0,
2x + 15 > 0
x 1– 2x 15+
x 1–()2x 15+()
2 x+
10
------------- -
2
x 1+
------------- -
§ 11. Логарифмические уравнения 57
18. 0,5lg(x
2
– 10x + 25) + lg (x
2
– 6x + 3) =
= 2lg(x – 5) + 0,5 lg 25.
19. lg – lg x – lg = 0.
10. lg (x(x + 9)) + lg = 0.
11. log
2
(2x
2
– 2) = log
2
(5x – 4).
12. = 3.
13. log
x + 1
(x – 0,5) = log
x – 0,5
(x + 1).
14. (x
3
+ 3x
2
– 2x – 1) = log
2x
x + log
2x
2.
15. log
1 + x
(2x
3
+ 2x
2
– 3x + 1) = 3.
16. log
x + 1
(x
3
– 9x + 8) · log
x – 1
(x + 1) = 3.
17. log
x + 1
(x
2
+ x – 6)
2
= 4.
18. (9 – 16x
4
) = 2 + .
19. log
3x
+ = 1.
20. log
x
16 + log
2x
64 = 3.
21. 20 log
4x
+ 7 log
16x
x
3
– 3 log
x/2
x
2
= 0.
22. log
x
2 – log
4
x + = 0.
23. 2 – (1 + x) = 3 log
b
– (x
2
– 1)
2
.
24. 3log
x
4 + 2 log
4x
4 + 3 log
16x
4 = 0.
Сведение заменой переменных алебраичесом равне-
нию. Пусть лоарифмичесое уравнение имеет вид
f(log
a
x) = 0,
де f(x) — неоторая фунция от x. Тода заменой y = log
a
x
оно сводится уравнениям вида (1):
log
a
x = y
i
,
де y
i
— орни уравнения f(y) = 0.
Пример 3. Решить уравнение
(log
2
x)
2
– 5 log
2
x + 6 = 0.
1
10
------
x
2
4x–4+
3
1
2
---
1
x
-------
x 9+
x
------------- -
lg 35 x
3
–()
lg 5 x–()
-------------------------------
log
x
3
2x
2
3x–5++
log
34x
2
–
1
log
2
34x
2
–()
------------------------------------- -
3
x
---
log
3
2
x
x
7
6
---
log
b
2
x 1– log
b
4
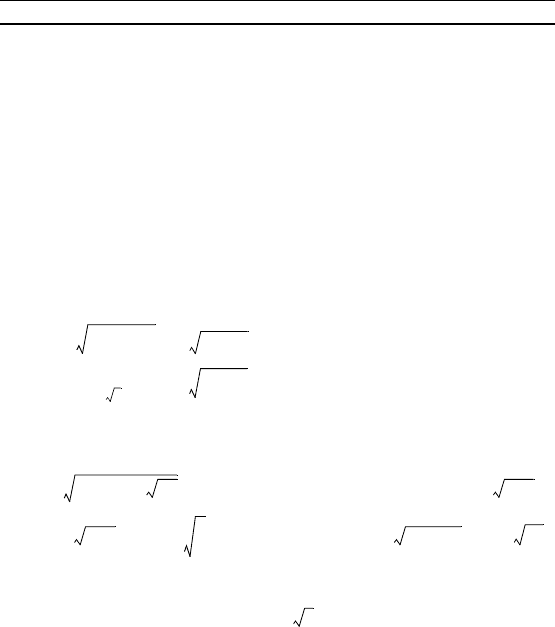
58 Г л а в а 2. Уравнения
Р е ш е н и е. Полаая log
2
x = y, получаем уравнение
y
2
– 5y + 6 = 0,
орнями отороо являются y
1
= 2, y
2
= 3. Следовательно, ис-
ходное уравнение эвивалентно двум уравнениям вида (1):
log
2
x = 2, log
2
x = 3,
имеющим решения x
1
= 4 и x
2
= 8.
Ответ. x
1
= 4, x
2
= 8.
Решите уравнение:
25. lg
3
x – lg
2
x – 6 lg x = 0.
26. 2 – – 6 = 0.
27. x – 30 + 36 = 0.
28. log
1/9
· log
1/9
x tg
2
= 2 cos
2
.
29. log
3
x + 1 = 0. 30. 4 – lg x = 3 .
31. 3 + 2lg = 2.
32. = lg .
33. log
3
( – 1)log
3
( – 3) = 6.
34. 2log
2
log
2
x + log
1/2
log
2
(2 x) = 1.
Метод лоарифмирования. Если неизвестное в уравнении
содержится а под знаом лоарифма, та и в основании сте-
пени, то в неоторых случаях таое уравнение можно решить
лоарифмированием обеих ео частей с последующим исполь-
зованием приведенных выше методов решения.
П р и м е р 4. Решить уравнение
= 3
8
.
Р е ш е н и е. Пролоарифмируем обе части уравнения по
основанию 3:
log
3
() = log
3
3
8
.
Используя свойства лоарифмов, получаем уравнение
(2 + log
3
x)log
3
x = 8.
2log
16
2
x
3
log
2
x
3
3
4
---
log
3
3
log
3
3
x
x
27
------
π
3
---
4π
3
------ -
1log
x
27+ lg x
lg x
1
x
---
lg x–() x
2
3
x
3
x 1+
2
x
2log
3
x+
x
2log
3
x+
§ 11. Логарифмические уравнения 59
Полаая log
3
x = y и выполнив замену переменных, прихо-
дим вадратному уравнению
y
2
+ 2y – 8 = 0,
имеющему орни y
1
= – 4, y
2
= 2. Наонец, решив простейшие
лоарифмичесие уравнения, находим орни исходноо урав-
нения:
log
3
x = –4 _ x = 3
–4
,log
3
x = 2 _ x = 3
2
.
Ответ. x
1
= 3
2
, x
2
= 3
–4
.
Решите уравнение:
35. = .
36. = .
37. = 10x
3
.
38. = 1.
39. 9x
lg x
+ 9x
–lg x
= 60.
40. + = 3.
41. = .
42. 7 · = 5 + .
Использование свойств лоарифмичесой фнции. Нео-
торые лоарифмичесие уравнения удается решить с помощью
исследования поведения фунций, входящих в левую и правую
части уравнения.
Пример 5. Решить уравнение
log
7
(x + 2) = 6 – x.
Р е ш е н и е. Подстановой убеждаемся, что x = 5 является
решением уравнения. Друих решений уравнение не имеет, та
а фунция f(x) = log
7
(x + 2) возрастает, а фунция g(x) = 6 – x
убывает, и, следовательно, рафии этих фунций не моут иметь
более одной точи пересечения.
Ответ. x = 5.
x
2lg
3
x 1,5 lg x–
10
x
lg
2
x lg x
3
3++
2
1
x 1+1–
----------------------------
1
x 1+1+
---------------------------- -
–
-----------------------------------------------------------------
x
2lg
2
x
15
log
5
3
x
log
5
9x 1+
x
log
2
2
x
2
log
2
2x–2–
(x 2)+
log
(x 2)+
2
4
x
3
log
3
x
2
()
3
-------------------------- -
x()
log
3
x–
1
log
3
x
--------------------
+
x
3
log
2
x
2
()
3
-------------------------- -
log
x
1
22
-----------
+
x 7+()
2
log
2
x 7+()
---------------------------------- -
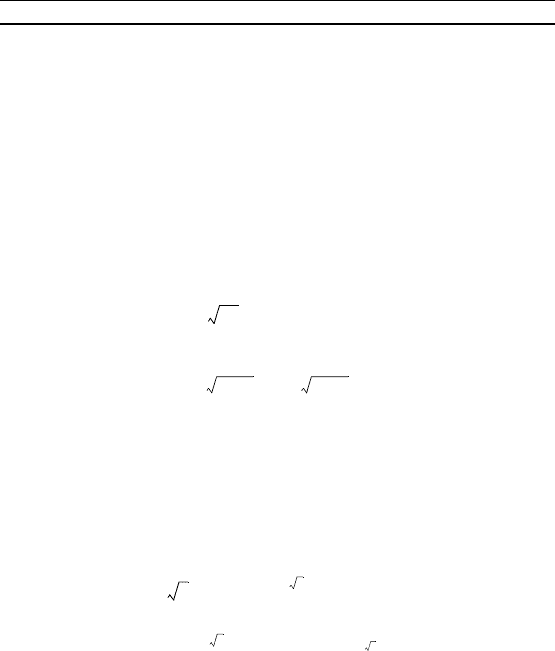
58 Г л а в а 2. Уравнения
Р е ш е н и е. Полаая log
2
x = y, получаем уравнение
y
2
– 5y + 6 = 0,
орнями отороо являются y
1
= 2, y
2
= 3. Следовательно, ис-
ходное уравнение эвивалентно двум уравнениям вида (1):
log
2
x = 2, log
2
x = 3,
имеющим решения x
1
= 4 и x
2
= 8.
Ответ. x
1
= 4, x
2
= 8.
Решите уравнение:
25. lg
3
x – lg
2
x – 6 lg x = 0.
26. 2 – – 6 = 0.
27. x – 30 + 36 = 0.
28. log
1/9
· log
1/9
x tg
2
= 2 cos
2
.
29. log
3
x + 1 = 0. 30. 4 – lg x = 3 .
31. 3 + 2lg = 2.
32. = lg .
33. log
3
( – 1)log
3
( – 3) = 6.
34. 2log
2
log
2
x + log
1/2
log
2
(2 x) = 1.
Метод лоарифмирования. Если неизвестное в уравнении
содержится а под знаом лоарифма, та и в основании сте-
пени, то в неоторых случаях таое уравнение можно решить
лоарифмированием обеих ео частей с последующим исполь-
зованием приведенных выше методов решения.
П р и м е р 4. Решить уравнение
= 3
8
.
Р е ш е н и е. Пролоарифмируем обе части уравнения по
основанию 3:
log
3
() = log
3
3
8
.
Используя свойства лоарифмов, получаем уравнение
(2 + log
3
x)log
3
x = 8.
2log
16
2
x
3
log
2
x
3
3
4
---
log
3
3
log
3
3
x
x
27
------
π
3
---
4π
3
------ -
1log
x
27+ lg x
lg x
1
x
---
lg x–() x
2
3
x
3
x 1+
2
x
2log
3
x+
x
2log
3
x+
§ 11. Логарифмические уравнения 59
Полаая log
3
x = y и выполнив замену переменных, прихо-
дим вадратному уравнению
y
2
+ 2y – 8 = 0,
имеющему орни y
1
= – 4, y
2
= 2. Наонец, решив простейшие
лоарифмичесие уравнения, находим орни исходноо урав-
нения:
log
3
x = –4 _ x = 3
–4
,log
3
x = 2 _ x = 3
2
.
Ответ. x
1
= 3
2
, x
2
= 3
–4
.
Решите уравнение:
35. = .
36. = .
37. = 10x
3
.
38. = 1.
39. 9x
lg x
+ 9x
–lg x
= 60.
40. + = 3.
41. = .
42. 7 · = 5 + .
Использование свойств лоарифмичесой фнции. Нео-
торые лоарифмичесие уравнения удается решить с помощью
исследования поведения фунций, входящих в левую и правую
части уравнения.
Пример 5. Решить уравнение
log
7
(x + 2) = 6 – x.
Р е ш е н и е. Подстановой убеждаемся, что x = 5 является
решением уравнения. Друих решений уравнение не имеет, та
а фунция f(x) = log
7
(x + 2) возрастает, а фунция g(x) = 6 – x
убывает, и, следовательно, рафии этих фунций не моут иметь
более одной точи пересечения.
Ответ. x = 5.
x
2lg
3
x 1,5 lg x–
10
x
lg
2
x lg x
3
3++
2
1
x 1+1–
----------------------------
1
x 1+1+
---------------------------- -
–
-----------------------------------------------------------------
x
2lg
2
x
15
log
5
3
x
log
5
9x 1+
x
log
2
2
x
2
log
2
2x–2–
(x 2)+
log
(x 2)+
2
4
x
3
log
3
x
2
()
3
-------------------------- -
x()
log
3
x–
1
log
3
x
--------------------
+
x
3
log
2
x
2
()
3
-------------------------- -
log
x
1
22
-----------
+
x 7+()
2
log
2
x 7+()
---------------------------------- -
