Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.



Москва
ОНИКС
Мир и Образование
2007
А. Г. ЦЫПКИН, А. И. ПИНСКИЙ
СПРАВОЧНОЕ
ПОСОБИЕ
ПО МАТЕМАТИКЕ
С МЕТОДАМИ РЕШЕНИЯ ЗАДАЧ
ДЛЯ ПОСТУПАЮЩИХ В ВУЗЫ
3-е издание, исправленное
УДК 51(075.3)
ББК 22.1я72
Ц97
Цыпкин А. Г.
Справочное пособие по математике с методами реше-
ния задач для поступающих в вузы / А. Г. Цыпкин,
А. И. Пинский. — 3-е изд., испр. — М.: ООО «Изда-
тельство Оникс»: ООО «Издательство «Мир и Образова-
ние», 2007. — 640 с.: ил.
ISBN 5-488-00721-0 (ООО «Издательство Оникс»)
ISBN 5-94666-341-0 (ООО «Издательство «Мир и Образование»)
Данное справочное пособие включает все основные разде-
лы школьной программы по математике.
Книга содержит необходимые теоретические сведения и
методы решения задач, иллюстрируемые подробно разобран-
ными примерами. Упражнения для самостоятельного реше-
ния включают задачи, предлагавшиеся на вступительных эк-
заменах в вузы с повышенными требованиями к математи-
ческой подготовке абитуриентов. Приводятся ответы, указа-
ния или решения ко всем упражнениям.
Пособие адресовано учащимся старших классов, абитури-
ентам и учителям математики.
УДК 51(075.3)
ББК 22.1я72
ISBN 5-488-00721-0
(ООО «Издательство Оникс»)
ISBN 5-94666-341-0
(ООО «Издательство «Мир и Образование»)
© Арманд Р. П., наследник, 2007
© Оформление переплета.
ООО «Издательство Оникс», 2007
Ц97
От издательства
Настоящее учебное пособие представляет собой третье,
переработанное и исправленное издание нии тех же
авторов (первые два издания под названием «Справочни
по методам решения задач по математие для средней
шолы» были выпущены в 1983 и 1989 .). Оно пред-
назначено для учащихся, желающих систематизировать,
улубить и расширить свои знания по математие, для
тоо чтобы лучше подотовиться выпусным эзаме-
нам в шоле и вступительным эзаменам в вуз.
Цель нии — изложить методы решения задач из
урса математии средней шолы, а таже тех задач,
оторым в шоле по тем или иным причинам не уде-
ляется должноо внимания.
Попытой достинуть этой цели и определяется стру-
тура нии. В начале аждоо парарафа рато изложен
теоретичесий материал (определения, основные теоремы
и формулы), знание отороо необходимо для решения
задач данноо раздела. Это позволяет использовать ни-
у, не прибеая дополнительно шольным учебниам.
Затем уазывается метод решения задач аоо-либо
вида и рассматривается пример, в отором используется
этот метод. После этоо приводятся упражнения для само-
стоятельноо решения (о всем упражнениям в онце
нии даны ответы, а неоторым — уазания или ре-
шения).
Таая форма изложения, по мнению авторов, наибо-
лее удобна для ативноо усвоения методов решения за-
дач. В ряде случаев при рассмотрении примеров дается,
возможно, не самое оротое и изящное решение. Это
объясняется прежде всео тем, что при решении примеров
авторы в первую очередь стремились дать налядное пред-
ставление о предложенном методе, а вовсе не о демон-
страции нестандартных подходов решению различных

4 От издательства
задач. Упражнения для самостоятельноо решения в ос-
новном взяты из вариантов, предлаавшихся на вступи-
тельных эзаменах по математие в вузы с повышен-
ными требованиями математичесой подотове аби-
туриентов.
В ние таже содержится материал, выходящий за
рами ныне действующей прораммы по математие для
учащихся средних шол: например, уравнения и неравен-
ства, содержащие обратные трионометричесие фун-
ции (§ 27 и § 29 л. 5); омплесные числа (§§ 31—34
л. 6); непрерывность фунции в точе (§ 44 л. 8); ряд
задач на омбинации мнооранниов и фиур вращения
(§ 75 л. 13); ряд задач, решаемых с помощью метода о-
ординат и методов веторной алебры (§ 78 и § 80 л. 14).
Однао авторы полаают, что изучение этоо материала
будет способствовать развитию и повышению математи-
чесой ультуры учащихся, а таже принесет пользу
при дальнейшем обучении в вузе. Безусловно, уазанный
дополнительный материал будет полезен учащимся шол,
лицеев и имназий, изучающих математиу по расши-
ренной прорамме.
Для удобства пользования ниой в ней приняты сле-
дующие обозначения: рядом с номерами тех упражне-
ний, оторым даны уазания или решения, ставятся
соответственно знаи
и ; те же знаи ставятся и в он-
це нии перед уазаниями или решениями.
При подотове настоящео издания нии ее науч-
ное и литературное редатирование, переработу части
материала, проверу мноих решений и ответов, устра-
нение замеченных неточностей и опечато выполнил
А. М. Суходсий.
Издательство будет блаодарно всем, то пришлет
свои замечания, советы и пожелания, связанные с этой
ниой.
Желаем вам успехов!
Глава 1
Преобразование
алгебраических выражений
При преобразованиях алебраичесих выражений исполь-
зуют формулы соращенноо умножения и правила действий
со степенями.
Формлы соращенноо множения
(a + b)(a – b) = a
2
– b
2
,(1)
(a
2
+ ab + b
2
)(a – b) = a
3
– b
3
,(2)
(a
2
– ab + b
2
)(a + b) = a
3
+ b
3
, (3)
(a + b)
2
= a
2
+ 2ab + b
2
,(4)
(a – b)
2
= a
2
– 2ab + b
2
,(5)
(a + b)
3
= a
3
+ 3a
2
b + 3ab
2
+ b
3
, (6)
(a – b)
3
= a
3
– 3a
2
b + 3ab
2
– b
3
.(7)
Правила действий со степенями
Если a > 0, то
a
m
· a
n
= a
m + n
,(8)
(a
m
)
n
= a
mn
,(9)
a
0
= 1, (10)
a
m
: a
n
= a
m – n
,(11)
= a
m/n
, n − 0, (12)
a
–n
= . (13)
Если a > 0, b > 0, n Ý N, то
= , (14)
= . (15)
a
m
n
1
a
---
n
ab
n
a
n
b
n
a
b
---
n
a
n
b
n
--------

4 От издательства
задач. Упражнения для самостоятельноо решения в ос-
новном взяты из вариантов, предлаавшихся на вступи-
тельных эзаменах по математие в вузы с повышен-
ными требованиями математичесой подотове аби-
туриентов.
В ние таже содержится материал, выходящий за
рами ныне действующей прораммы по математие для
учащихся средних шол: например, уравнения и неравен-
ства, содержащие обратные трионометричесие фун-
ции (§ 27 и § 29 л. 5); омплесные числа (§§ 31—34
л. 6); непрерывность фунции в точе (§ 44 л. 8); ряд
задач на омбинации мнооранниов и фиур вращения
(§ 75 л. 13); ряд задач, решаемых с помощью метода о-
ординат и методов веторной алебры (§ 78 и § 80 л. 14).
Однао авторы полаают, что изучение этоо материала
будет способствовать развитию и повышению математи-
чесой ультуры учащихся, а таже принесет пользу
при дальнейшем обучении в вузе. Безусловно, уазанный
дополнительный материал будет полезен учащимся шол,
лицеев и имназий, изучающих математиу по расши-
ренной прорамме.
Для удобства пользования ниой в ней приняты сле-
дующие обозначения: рядом с номерами тех упражне-
ний, оторым даны уазания или решения, ставятся
соответственно знаи
и ; те же знаи ставятся и в он-
це нии перед уазаниями или решениями.
При подотове настоящео издания нии ее науч-
ное и литературное редатирование, переработу части
материала, проверу мноих решений и ответов, устра-
нение замеченных неточностей и опечато выполнил
А. М. Суходсий.
Издательство будет блаодарно всем, то пришлет
свои замечания, советы и пожелания, связанные с этой
ниой.
Желаем вам успехов!
Глава 1
Преобразование
алгебраических выражений
При преобразованиях алебраичесих выражений исполь-
зуют формулы соращенноо умножения и правила действий
со степенями.
Формлы соращенноо множения
(a + b)(a – b) = a
2
– b
2
,(1)
(a
2
+ ab + b
2
)(a – b) = a
3
– b
3
,(2)
(a
2
– ab + b
2
)(a + b) = a
3
+ b
3
, (3)
(a + b)
2
= a
2
+ 2ab + b
2
,(4)
(a – b)
2
= a
2
– 2ab + b
2
,(5)
(a + b)
3
= a
3
+ 3a
2
b + 3ab
2
+ b
3
, (6)
(a – b)
3
= a
3
– 3a
2
b + 3ab
2
– b
3
.(7)
Правила действий со степенями
Если a > 0, то
a
m
· a
n
= a
m + n
,(8)
(a
m
)
n
= a
mn
,(9)
a
0
= 1, (10)
a
m
: a
n
= a
m – n
,(11)
= a
m/n
, n − 0, (12)
a
–n
= . (13)
Если a > 0, b > 0, n Ý N, то
= , (14)
= . (15)
a
m
n
1
a
---
n
ab
n
a
n
b
n
a
b
---
n
a
n
b
n
--------

6Глава1. Преобразование алгебраических выражений
Если a < 0, b < 0, n = 2k, k Ý N, то
= , (16)
= . (17)
Если n = 2k + 1, k Ý N, то
= , (18)
= , b − 0. (19)
Если n Ý N, m Ý N, то
= . (20)
§1.Упрощение
иррациональных выражений
Под упрощением иррациональноо выражения понимают
приведение ео виду, содержащему меньшее число алебраи-
чесих операций над входящими в исходное выражение пере-
менными.
Для упрощения иррациональноо выражения часто разла-
ают исходное выражение на множители, а затем выносят об-
щий множитель за соби.
П р и м е р 1. Упростить выражение
+ – .
Решение.Выделим общий множитель в числителе и
знаменателе первой дроби данноо выражения. Для этоо пред-
ставим числитель в виде
a + b = a
3/2
+ b
3/2
= + .
Используя формулу (3), получаем
+ = (a
1/2
+ b
1/2
) (a – a
1/2
b
1/2
+ b).
ab
n
a
n
b
n
a
b
---
n
a
n
b
n
-----------
ab
n
a
n
b
n
a
b
---
n
a
n
b
n
--------
a
2m
2n
a
m
n
aa bb+
ab+()ab–()
---------------------------------------------
2 b
ab+
--------------------- -
ab
ab–
------------ -
a b (a
1/2
)
3
(b
1/2
)
3
(a
1/2
)
3
(b
1/2
)
3
§ 1. Упрощение иррациональных выражений 7
Множитель a
1/2
+ b
1/2
= + является общим для числи-
теля и знаменателя дроби. После ее соращения данное выра-
жение примет вид
+ – . (*)
Приведя выражение (*) общему знаменателю, имеем
= = 1.
Ответ. 1.
Упростите выражение:
1. · .
2. – (ab)
–1/2
.
3. a + b .
4. – (y
–1/2
– x
–1/2
).
5. ( – + + ) : .
6. .
7. : .
8. : .
a
b
aab– b+
ab–
-------------------------------
2 b
ab+
--------------------- -
ab
ab–
------------ -
aab– b 2 ab 2b– ab–++
ab–
------------------------------------------------------------------------------------ -
ab–
ab–
------------ -
xy–
xy–
--------------------- -
xy–
xy+
----------------------
–
xy–
xy–
--------------------- -
xy+
xy–
----------------------
+
--------------------------------------------------- -
2 xy
yx–
---------------
1
(a
1/2
b
1/2
)+
2–
----------------------------------------
ab–
a
3/2
b
3/2
–
----------------------------
1–
ab+
2ba
--------------------- -
1–
ab+
2ab
--------------------- -
1–
x
1/2
y
1/2
+
x
1/2
y
1/2
–
-----------------------------
x
1/2
y
1/2
–
x
1/2
y
1/2
+
-----------------------------
( a
4
b
4
)
2–
( a
4
b
4
)
2–
ab+
ab–
--------------------- -
2
a
1/m
a
1/n
–()
2
4a
mn+()/mn
+
a
2/ m
a
2/ n
–()a
m 1+
m
a
n 1+
n
+()
------------------------------------------------------------------------------------------
1
a 1–
-----------------
a 1–+
1
a 1+
------------------
–
1
a 1–
-----------------
------------------------------------------ -
a 1–
a 1–()a 1+ a 1+()a 1––
-------------------------------------------------------------------------------- -
ab+()
2
4b–
ab–() :
1
b
---
+3
1
a
---
---------------------------------------------------------
a 9b 6 ab++
1
b
------ -
1
a
-------
+
---------------------------------------
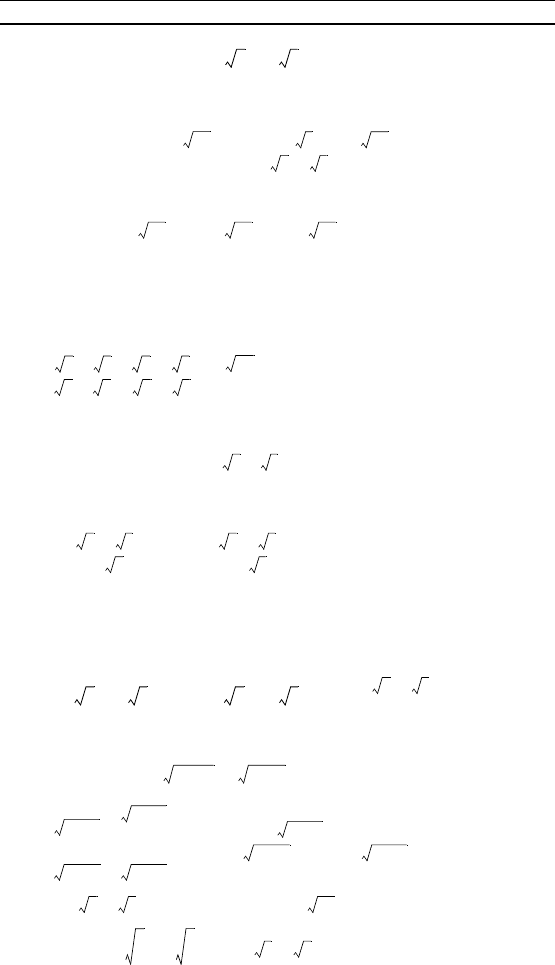
6Глава1. Преобразование алгебраических выражений
Если a < 0, b < 0, n = 2k, k Ý N, то
= , (16)
= . (17)
Если n = 2k + 1, k Ý N, то
= , (18)
= , b − 0. (19)
Если n Ý N, m Ý N, то
= . (20)
§1.Упрощение
иррациональных выражений
Под упрощением иррациональноо выражения понимают
приведение ео виду, содержащему меньшее число алебраи-
чесих операций над входящими в исходное выражение пере-
менными.
Для упрощения иррациональноо выражения часто разла-
ают исходное выражение на множители, а затем выносят об-
щий множитель за соби.
П р и м е р 1. Упростить выражение
+ – .
Решение.Выделим общий множитель в числителе и
знаменателе первой дроби данноо выражения. Для этоо пред-
ставим числитель в виде
a + b = a
3/2
+ b
3/2
= + .
Используя формулу (3), получаем
+ = (a
1/2
+ b
1/2
) (a – a
1/2
b
1/2
+ b).
ab
n
a
n
b
n
a
b
---
n
a
n
b
n
-----------
ab
n
a
n
b
n
a
b
---
n
a
n
b
n
--------
a
2m
2n
a
m
n
aa bb+
ab+()ab–()
---------------------------------------------
2 b
ab+
--------------------- -
ab
ab–
------------ -
a b (a
1/2
)
3
(b
1/2
)
3
(a
1/2
)
3
(b
1/2
)
3
§ 1. Упрощение иррациональных выражений 7
Множитель a
1/2
+ b
1/2
= + является общим для числи-
теля и знаменателя дроби. После ее соращения данное выра-
жение примет вид
+ – . (*)
Приведя выражение (*) общему знаменателю, имеем
= = 1.
Ответ. 1.
Упростите выражение:
1. · .
2. – (ab)
–1/2
.
3. a + b .
4. – (y
–1/2
– x
–1/2
).
5. ( – + + ) : .
6. .
7. : .
8. : .
a
b
aab– b+
ab–
-------------------------------
2 b
ab+
--------------------- -
ab
ab–
------------ -
aab– b 2 ab 2b– ab–++
ab–
------------------------------------------------------------------------------------ -
ab–
ab–
------------ -
xy–
xy–
--------------------- -
xy–
xy+
----------------------
–
xy–
xy–
--------------------- -
xy+
xy–
----------------------
+
--------------------------------------------------- -
2 xy
yx–
---------------
1
(a
1/2
b
1/2
)+
2–
----------------------------------------
ab–
a
3/2
b
3/2
–
----------------------------
1–
ab+
2ba
--------------------- -
1–
ab+
2ab
--------------------- -
1–
x
1/2
y
1/2
+
x
1/2
y
1/2
–
-----------------------------
x
1/2
y
1/2
–
x
1/2
y
1/2
+
-----------------------------
( a
4
b
4
)
2–
( a
4
b
4
)
2–
ab+
ab–
--------------------- -
2
a
1/m
a
1/n
–()
2
4a
mn+()/mn
+
a
2/ m
a
2/ n
–()a
m 1+
m
a
n 1+
n
+()
------------------------------------------------------------------------------------------
1
a 1–
-----------------
a 1–+
1
a 1+
------------------
–
1
a 1–
-----------------
------------------------------------------ -
a 1–
a 1–()a 1+ a 1+()a 1––
-------------------------------------------------------------------------------- -
ab+()
2
4b–
ab–() :
1
b
---
+3
1
a
---
---------------------------------------------------------
a 9b 6 ab++
1
b
------ -
1
a
-------
+
---------------------------------------
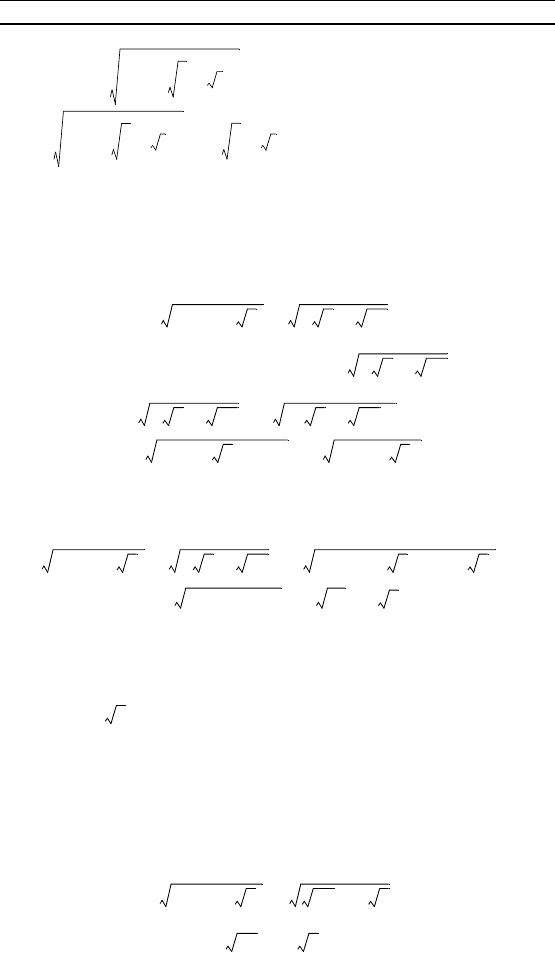
8Глава1. Преобразование алгебраических выражений
9. .
Инода выражения, содержащие произведение радиалов
с различными поазателями степени, удается упростить, при-
ведя все радиалы одному поазателю.
П р и м е р 2. Упростить выражение
· .
Р е ш е н и е. Преобразуем радиал та:
= =
= = .
Тода исходное выражение преобразуется следующим обра-
зом:
· = =
= = =
(при
переходе
последнему
выражению
зна
модуля
мож-
но опустить, та а исходное выражение определено тольо
при x l 0).
Ответ..
При преобразовании радиалов необходимо учитывать, что
по определению орень четной степени есть величина неотри-
цательная, в то время а орень нечетной степени может быть
а неотрицательной, та и отрицательной величиной.
П р и м е р 3. Упростить выражение
· .
Р е ш е н и е. Та а – 2 m 0 (в чем можно убедить-
ся, сравнив вадраты уменьшаемоо и вычитаемоо), то перед
21
1
4
---
1
t
---
t–
2
+
1
1
4
---
1
t
---
t–
2
+
1
2
---
1
t
---
t–
–
--------------------------------------------------------------------------------------- -
x 743+()
4
2 x 3x–
2 x 3x–
2 x 3x– 2 x 3x–()
2
4
4x 43x–3x+
4
7x 43x–
4
x 743+()
4
2 x 3x– x
2
743+()743–()
4
x
2
49 48–()
4
x
2
4
x
x
x 743+()
6
3x 2 x–
3
3x x
§ 2. Преобразование выражений, содержащих знак модуля 9
приведением радиалов общему поазателю представим вто-
рой сомножитель в виде
= – = – .
Дальнейшее упрощение выполним по схеме предыдущео
примера:
· = – · =
= – = – .
Ответ.– .
Упростите выражение:
10. · .
11. · .
12. .
13. .
14. .
15. · +
+ : + 1 .
16. .
§ 2. Преобразование выражений,
содержащих знак модуля
Преобразование выражений, в оторых наряду с арифмети-
чесими операциями присутствует зна модуля (абсолютной ве-
личины) от неоторой фунции, обычно производят отдельно
на аждом промежуте знаопостоянства этой фунции.
3x 2 x–
3
2 x 3x–
3
2 x 3x–()
2
6
x 743+()
6
3x 2 x–
3
x 743+()
6
3x 2 x–()
2
6
x
2
49 48–()
6
x
3
x
3
6x 526+()
4
32x 23x–
4x 11 4 6+()
6
23x 42x–
3
2p 1+()
3
2p 1–()
3
+
4p 24p
2
1–+
----------------------------------------------------------------- -
x 2 x
2
–+
3
1 x 2 x
2
––
6
⋅
1 x
2
–
3
-------------------------------------------------------------------------------- -
26 15 3–
3
23–()
743–
--------------------------------------------------------
1
2
---
20 14 2+
3
642–
1
2
---
a 3+()a 3a–1–
3
a 1–
2 a 1+()
-------------------------- -
2b 2 b
2
4––
b
2
4– b 2+()–
---------------------------------------------
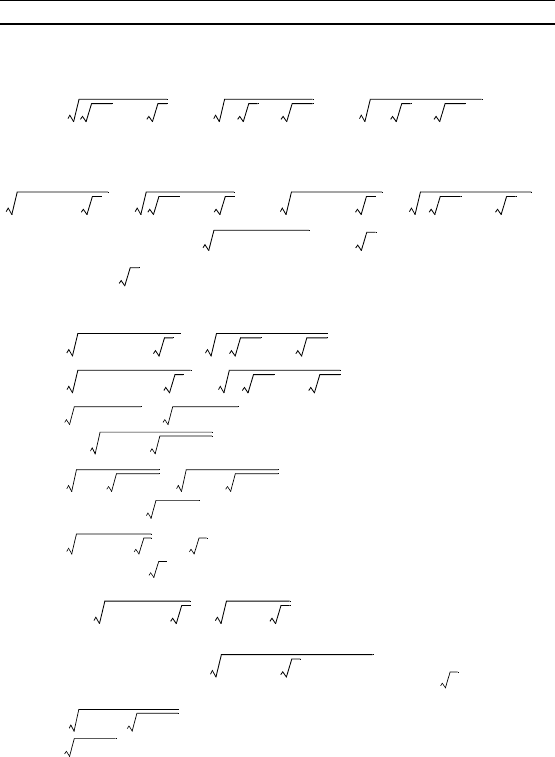
8Глава1. Преобразование алгебраических выражений
9. .
Инода выражения, содержащие произведение радиалов
с различными поазателями степени, удается упростить, при-
ведя все радиалы одному поазателю.
П р и м е р 2. Упростить выражение
· .
Р е ш е н и е. Преобразуем радиал та:
= =
= = .
Тода исходное выражение преобразуется следующим обра-
зом:
· = =
= = =
(при
переходе
последнему
выражению
зна
модуля
мож-
но опустить, та а исходное выражение определено тольо
при x l 0).
Ответ..
При преобразовании радиалов необходимо учитывать, что
по определению орень четной степени есть величина неотри-
цательная, в то время а орень нечетной степени может быть
а неотрицательной, та и отрицательной величиной.
П р и м е р 3. Упростить выражение
· .
Р е ш е н и е. Та а – 2 m 0 (в чем можно убедить-
ся, сравнив вадраты уменьшаемоо и вычитаемоо), то перед
21
1
4
---
1
t
---
t–
2
+
1
1
4
---
1
t
---
t–
2
+
1
2
---
1
t
---
t–
–
--------------------------------------------------------------------------------------- -
x 743+()
4
2 x 3x–
2 x 3x–
2 x 3x– 2 x 3x–()
2
4
4x 43x–3x+
4
7x 43x–
4
x 743+()
4
2 x 3x– x
2
743+()743–()
4
x
2
49 48–()
4
x
2
4
x
x
x 743+()
6
3x 2 x–
3
3x x
§ 2. Преобразование выражений, содержащих знак модуля 9
приведением радиалов общему поазателю представим вто-
рой сомножитель в виде
= – = – .
Дальнейшее упрощение выполним по схеме предыдущео
примера:
· = – · =
= – = – .
Ответ.– .
Упростите выражение:
10. · .
11. · .
12. .
13. .
14. .
15. · +
+ : + 1 .
16. .
§ 2. Преобразование выражений,
содержащих знак модуля
Преобразование выражений, в оторых наряду с арифмети-
чесими операциями присутствует зна модуля (абсолютной ве-
личины) от неоторой фунции, обычно производят отдельно
на аждом промежуте знаопостоянства этой фунции.
3x 2 x–
3
2 x 3x–
3
2 x 3x–()
2
6
x 743+()
6
3x 2 x–
3
x 743+()
6
3x 2 x–()
2
6
x
2
49 48–()
6
x
3
x
3
6x 526+()
4
32x 23x–
4x 11 4 6+()
6
23x 42x–
3
2p 1+()
3
2p 1–()
3
+
4p 24p
2
1–+
----------------------------------------------------------------- -
x 2 x
2
–+
3
1 x 2 x
2
––
6
⋅
1 x
2
–
3
-------------------------------------------------------------------------------- -
26 15 3–
3
23–()
743–
--------------------------------------------------------
1
2
---
20 14 2+
3
642–
1
2
---
a 3+()a 3a–1–
3
a 1–
2 a 1+()
-------------------------- -
2b 2 b
2
4––
b
2
4– b 2+()–
---------------------------------------------
