Циценкова Г.А., Чукавина Т.В., Рязанова Л.Д., Труппова В.А. Методические указания и контрольные задания по высшей математике
Подождите немного. Документ загружается.


61
⎩
⎨
⎧
=⋅+⋅
=⋅+⋅
.1,7310285
,3,22352858865
ba
ba
Для решения системы умножим первое уравнение на (-10), второе – на 285.
Сложив их, получим
5,15197425 =a
отсюда
.205,0
=
a
Тогда
.468,1
10
675,14
10
205,02851,73
==
⋅−
=
b
Следовательно, искомая аппроксимирующая функция имеет вид:
.468,1205,0 += xy
Замечание.
Систему уравнений можно решать любым способом.
Раздел 2. Неопределенный и определенный интегралы.
Вопросы для самоподготовки.
1. Неопределенный интеграл.
1.1.
Первообразная и ее свойства.
1.2.
Неопределенный интеграл и его свойства.
1.3.
Простейшие приемы интегрирования. Таблица основных интегралов.
1.4.
Замена переменной в неопределенном интеграле, интегрирование по
частям.
1.5.
Интегрирование: ∫
++
+
dx
cbxax
NMx
2
;
∫
++
+
dx
cbxax
NMx
2
.
1.6.
Интегрирование рациональных дробей.
1.7.
Интегрирование тригонометрических выражений. Универсальная
тригонометрическая подстановка.
1.8.
Интегрирование простейших иррациональностей.

62
2.
Определенный интеграл и его приложения.
2.1.
Определенный интеграл как предел интегральной суммы. Задачи,
приводящие к определенному интегралу. Необходимое условие
интегрируемости функции. Классы интегрирующих функций.
2.2.
Геометрический и механический смысл определенного интеграла.
2.3.
Основные свойства определенного интеграла.
2.4.
Формула Ньютона-Лейбница вычисления определенных интегралов.
2.5.
Замена переменной в определенном интеграле, интегрирование по
частям.
2.6.
Несобственные интегралы 1 и 2-го рода. Их свойства и вычисление.
Абсолютная и условная сходимость интеграла.
2.7.
Применения определенных интегралов в геометрии, механике, физике
(вычисление площадей, объемов и поверхностей тел вращения, длины
дуги, пройденного пути, работы силы и т.д.).
Контрольные задания
Задача 6.
Вычислить неопределенные интегралы. В двух первых примерах а) и б) проверить
результаты дифференцированием.
а)
∫
⋅ ;2sin
2
sin
xdxe
x
б)
∫
;dxxarctg
6.1.
в)
∫
+
;
8
3
x
dx
г)
∫
++
;
11
3
x
dx
6.2.
а)
∫
+
;
)4(
62
x
xdx
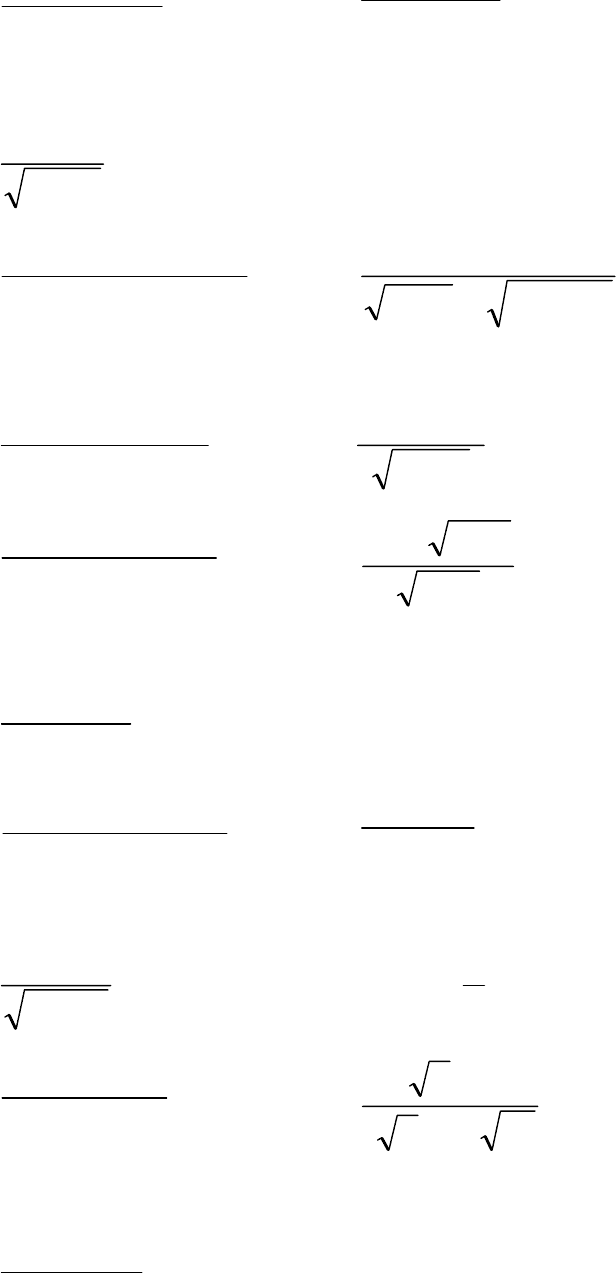
б)
∫
+⋅ .)31ln( dxee
xx
63
в)
∫
+
+−
;
1
132
3
2
dx
x
xx
г)
∫
+
.
sin tgxx
dx
а)
∫
−
;
1
8
3
x
dxx
б)
∫
⋅ .3 dxx
x
6.3.
в)
∫
+++
−
;
1644
)73(
23
xxx
dxx
г)
∫
+++
.
)3(3
3
2
xx
dx
а)
∫
+
;
)13(cos
2
tgxx
dx
б)
∫
−
.
1
arcsin
2
dx
x
xx
6.4.
в)
∫
+++
;
22
23
xxx
dx
г)
∫
+
++
.
1
1
3
2
dx
x
xx
а)
∫
+
;
3sin4
3cos
dx
x
x
б)
∫
.
32
dxex
x
6.5.
в)
∫
+
+
+
;
485
23
2
xxx
dxx
г)
∫
+
.
cos1
cos
dx
x
xdx
а)
∫
;
cos
sin
3
2
x
xdx
б)
∫
.
1
arcsin dx
x
x
6.6.
в)
∫
−+
+
;
2
)3(
23
xxx
dxx
г)
∫
+
+
.
)4(
)1(
4
3
4
dx
xx
x
6.7.
а)
∫
+
+
;
1
2
dx
x
arctgxx
б)
∫
+ .)1ln(
2
dxxx
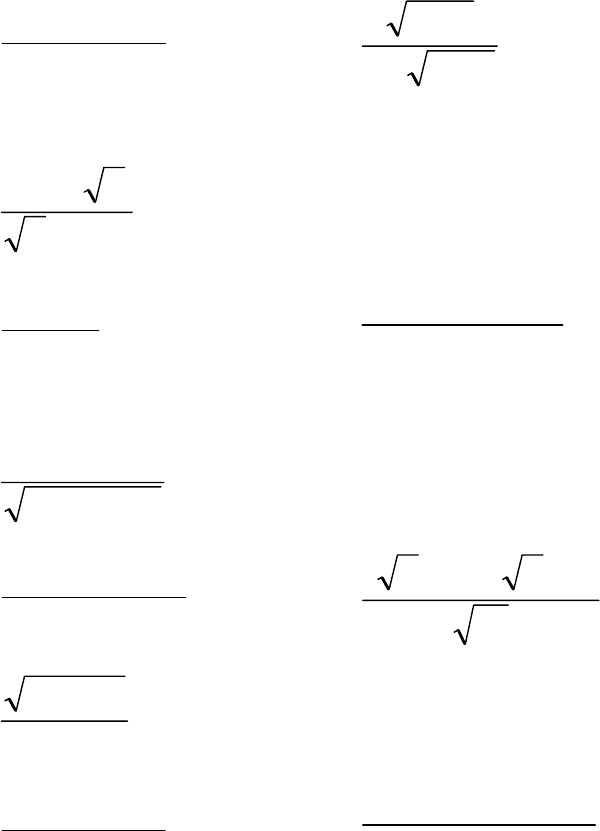
64
в)
∫
++
−
;
65
)3(
24
2
xx
dxx
г)
∫
++
+
.
51
5
3
dx
x
x
а)
∫
+
;
)1(
dx
xx
xarctg
б)
∫
.cossin xdxxx
6.8.
в)
∫
−
;
81
4
2
x
dxx
г)
∫
+
.
sin4cos3 xx
dx
а)
∫
+
;
cos23
sin
3
x
xdx
б)
∫
.4sin
2
xdxx
6.9.
в)
∫
−+
+−
;
32
)1(
24
2
xx
dxxx
г)
∫
+⋅−
.
)1()1(
3
2
6
dx
x
xx
а)
∫
+
;
ln4
3
dx
x
x
б)
∫
⋅ .ln
2
xdxx
6.10
.
в)
∫
++
−
;
86
)6(
24
3
xx
dxx
г)
∫
+
+
.
2cossin2 xx
dx
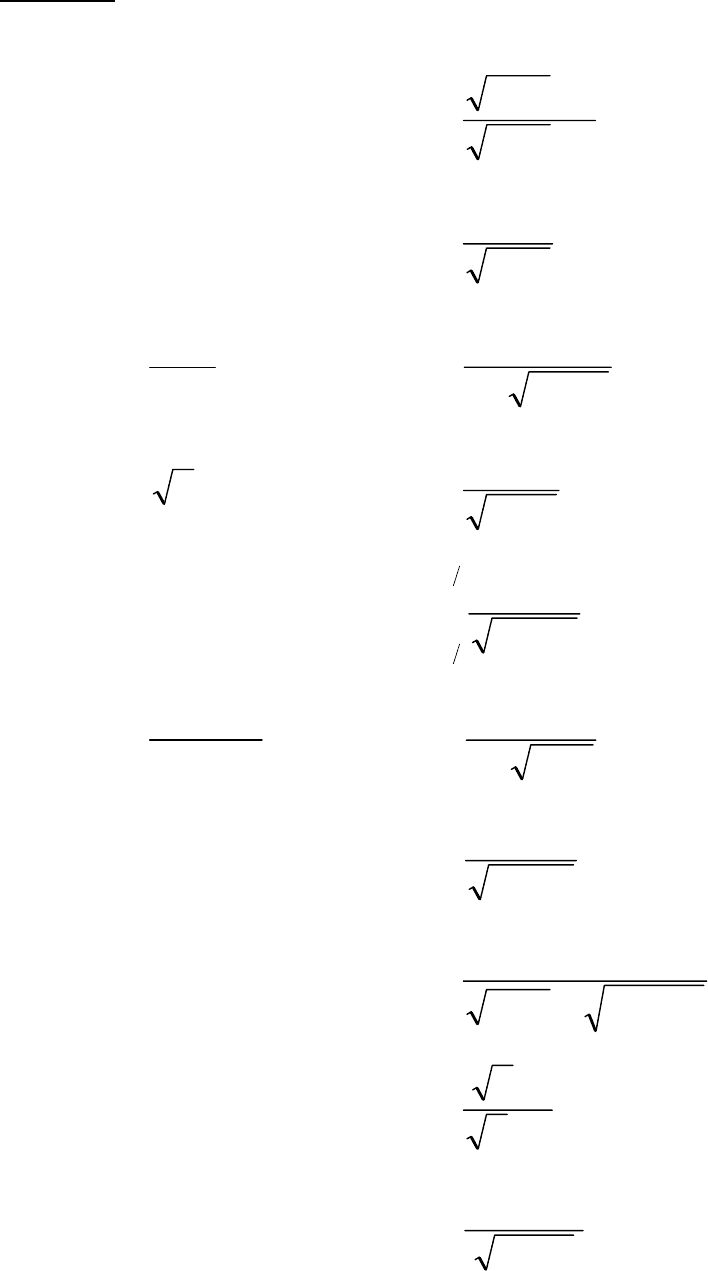
Задача 7.
Вычислить определенный интеграл.
7.1.
а)
∫
−⋅
3
2
;)1ln( dyyy
б)
∫
−+
++
8
3
;
11
11
dx
x
x
7.2.
а)
∫
−
2
1
;ln)1( ydyy
б)
∫
+
8
3
;
1x
xdx
7.3.
а)
∫
e
dx
x
x
1
2
2
;
ln
б)
∫
++
4
0
;
121 x
dx
7.4.
а)
∫
2
1
;ln
e
xdxx
б)
∫
+
5
0
;
4x
xdx
7.5.
а)
∫
⋅
2
1
2
;ln ydyy
б)
∫
+
37
32
;
32 x
xdx
7.6.
а)
∫
+
+
2
1
2
;
)1(
)1ln(
dx
x
x
б)
∫
−
++
0
1
3
;
11 x
dx
7.7.
а)
∫
⋅
e
xdxx
1
2
;ln
б)
∫
−
−
1
1
;
45 x
xdx
7.8.
а)
∫
−
−
0
1
;)1ln( dxxx
б)
∫
+++
2
0
3
;
)1(1 xx
dx
7.9.
а)
∫
+
2
1
;)23ln( dxx
б)
∫
−
9
4
;
1x
dxx
7.10.
а)
∫
⋅
1
0
;arctgxdxx
б)
∫
+
+
13
0
3
.
12
)1(
x
dxx

66
Задача 8.
Вычислить несобственный интеграл или исследовать его на сходимость.
8.1.
∫
∞
−
⋅
0
;
2
dxex
x
8.2.
∫
−
∞−
+
3
22
;
)1(x
xdx
8.3.
∫
∞
−
++
1
2
;
1xx
dx
8.4.
∫
−
1
0
3
2
;
1 x
dxx
8.5.
∫
−
2
1
2
;
)1(x
dx
8.6.
∫
−
+
2
3
2
;
)3(x
dx
8.7.
∫
∞
2
;
ln xx
dx
8.8.
∫
−
3
0
2
;
)2(x
dx
8.9.
∫
−
4
0
3
2
.
)3(x
dx
8.10.
∫
∞
∞−
++
.
54
2
xx
dx
Задача 9.
Вычислить площадь фигуры, ограниченной указанными линиями.
9.1.
.2cos3
ϕ
=r
9.2.
).cos1(2
ϕ
−
=
r
9.3.
.2cos3
ϕ
=r
9.4.
.2sin2
2
ϕ
=r
9.5.
).cos1(2
ϕ
+=r
9.6.
.3sin2
ϕ
=
r
9.7.
).sin1(3
ϕ
+=r
9.8.
.2sin4
ϕ
=
r
9.9.
.2cos4
2
ϕ
=r
9.10.
).sin1(4
ϕ
−
=
r
Задача 10.
Вычислить длину дуги данной линии.

67
10.1.
⎪
⎩
⎪
⎨
⎧
≤≤
−=
−=
π
20
),cos1(3
),sin(3
t
ty
ttx
10.2.
⎪
⎩
⎪
⎨
⎧
≤≤
−=
+=
π
t
ttty
tttx
0
),cos(sin2
),sin(cos2
10.3.
⎪
⎩
⎪
⎨
⎧
≤≤
=
=
20
,sin2
,cos2
3
3
π
t
ty
tx
10.4.
⎪
⎩
⎪
⎨
⎧
≤≤
=
=
20
,sin5
,cos5
2
2
π
t
ty
tx
10.5.
⎪
⎩
⎪
⎨
⎧
≤≤
−=
−=
π
20
),cos1(9
),sin(9
t
ty
ttx
10.6.
⎪
⎩
⎪
⎨
⎧
≤≤
=
=
ππ
t
ty
tx
2
,sin4
,cos4
3
3
10.7.
⎪
⎩
⎪
⎨
⎧
≤≤
−=
+=
π
t
ttty
tttx
0
),cos(sin4
),sin(cos4
10.8.
⎪
⎩
⎪
⎨
⎧
≤≤
−=
−=
ππ
42
),cos1(7
),sin(7
t
ty
ttx
10.9.
⎪
⎩
⎪
⎨
⎧
≤≤
=
=
ππ
t
ty
tx
2
,sin7
,cos7
2
2
10.10.
⎪
⎩
⎪
⎨
⎧
≤≤
−=
+=
π
t
ttty
tttx
0
),cos(sin5
),sin(cos5
Задача 11.
Вычислить объем тела, полученного вращением фигуры
Φ
вокруг указанной оси
координат.
11.1.
.,,:
22
OXyxxy ==Φ
11.2.
.,1,:
23
OXyxy ==Φ
11.3.
.,0,4:
2
OYxxy =−=Φ
11.4.
.,2,)1(:
32
OXxxy =−=Φ
11.5.
.),0(,0,sin: OXxyxy
π
≤≤
=
=Φ
11.6.
.,4,4:
22
OXyxxy ==Φ
11.7.
.,1,0,0,: OXxyxey
x
====Φ
11.8.
.,3,34:
2
OXxxy ==Φ
11.9.
.,0,2:
2
OXyxxy =−=Φ
11.10.
.,,2:
22
OXxyxy =−=Φ
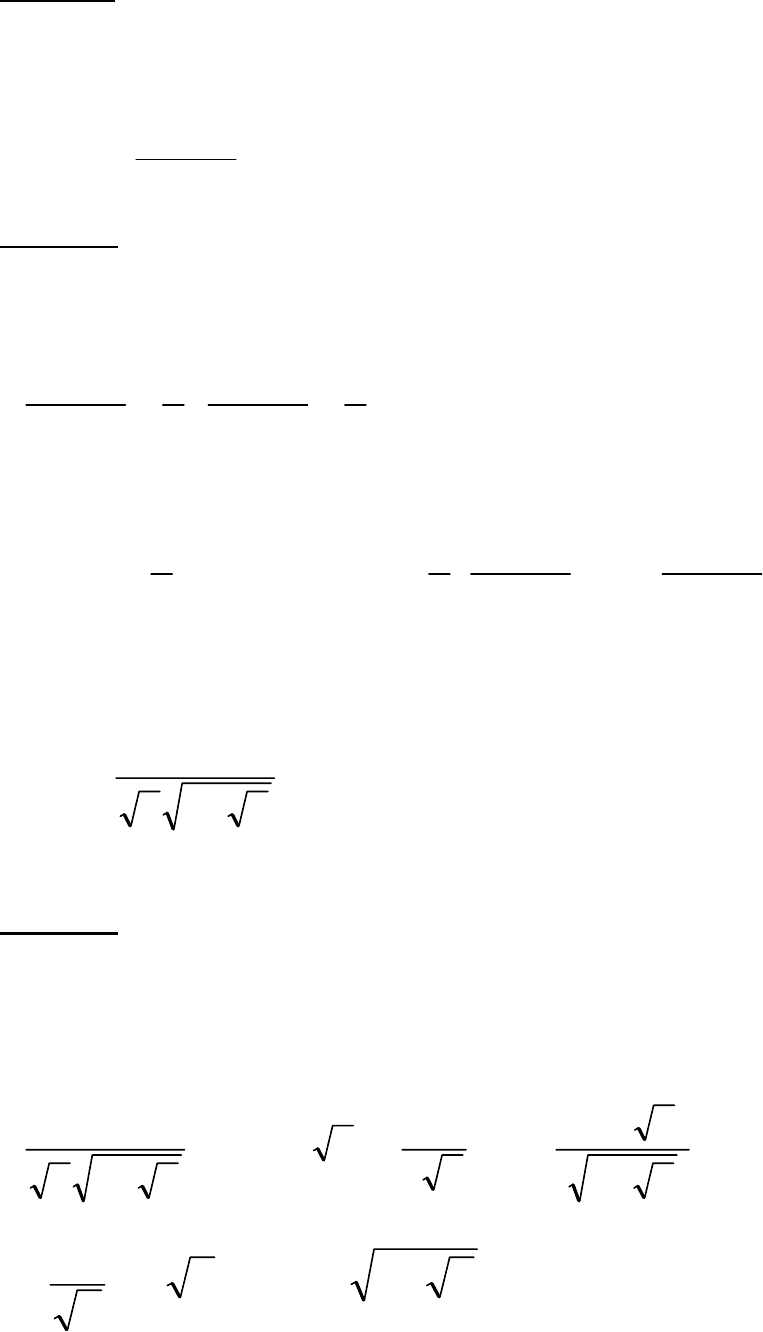
68
Решение типового варианта
Задача 6.
Найти неопределенные интегралы. В примерах 6.1 (а,б), 6.2 (а) результаты
интегрирования проверить дифференцированием.
6.1.
(а)
∫
+
.
43
7
2
x
xdx
Решение.
Преобразуем подынтегральную функцию так, чтобы в числителе получилась
производная знаменателя:
∫∫
++=
+
=
+
.)43ln(
6
7
43
6
6
7
43
7
2
22
cx
x
xdx
x
xdx
Проверка:
,
43
7
43
6
6
7
)43ln(
6
7
22
2
+
=
′
+
+
⋅=
′
⎟
⎠
⎞
⎜
⎝
⎛
++
x
x
c
x
x
cx
То есть производная от первообразной функции равна подынтегральной функции
[7].
6.1
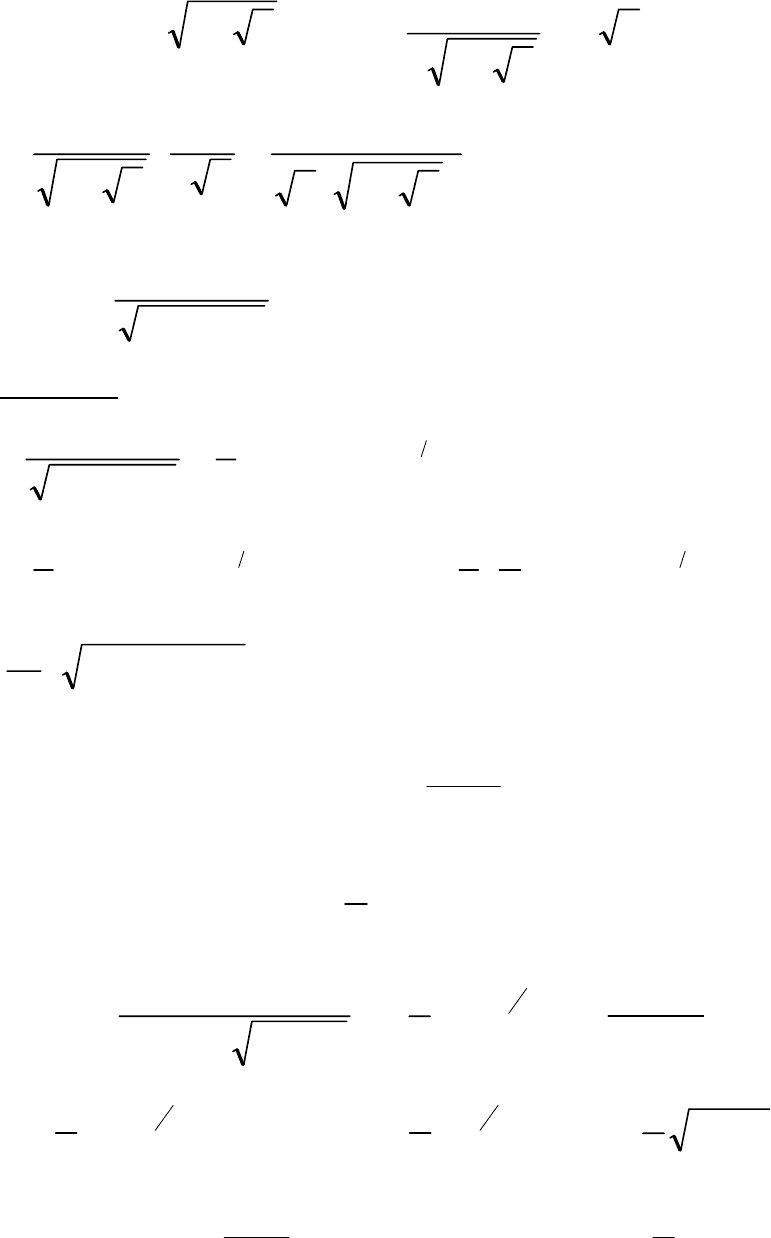
. (б)
∫
+ xx
dx
1
Решение.
Данный интеграл можно привести к табличному, если подвести часть
подынтегральной функции под знак дифференциала и ввести компенсирующий
множитель.
∫∫
=
+
+
=
⎭
⎬
⎫
⎩
⎨
⎧
=+=
+ x
xd
x
dx
xd
xx
dx
1
)1(
2
2
)1(
1
.142 cxcu
u
du
++=
⎭
⎬
⎫
⎩
⎨
⎧
+=
∫
69
Проверка:
=
′
+
′
+
+
=
′
⎟
⎠
⎞
⎜
⎝
⎛
++ cx
x
cx )1(
12
1
414
.
1
1
2
1
1
2
⎟
⎠
⎞
⎜
⎝
⎛
+
=⋅
+
=
xx
x
x
6.1
. (в)
∫
−
5
43sin
3cos
x
xdx
Решение.
∫∫
=⋅−=
−
−
xdxx
x
xdx
3cos3)43(sin
3
1
43sin
3cos
51
5
∫
=+−⋅=−−=
−
cxxdx
5451
)43(sin
4
5
3
1
)43(sin)43(sin
3
1
.)43(sin
12
5
5
4
cx +−⋅
Используется формула
∫
+
+
=
+
,
1
1
c
n
u
duu
n
n
где
5
1
,43sin −=−= nxu
.
6.1. (г)
=
⎟
⎠
⎞
⎜
⎝
⎛
−−=
⋅
∫∫
−
x
dx
xctg
xctgx
dx
4sin
4
4
4
1
44sin
2
3
2
3
22
.4
4
3
4
4
3
)4(4
4
1
3
3
1
3
2
cxctgcxctgxctgdxctg +−=+−=⋅−=
∫
−
так как
∫
+
+
=
+
,
1
1
c
n
u
duu
n
n
где
3
2
,4 −== nxctgu
.
6.1.
(д)
xdxe
x
sin
2cos3
⋅
∫
+
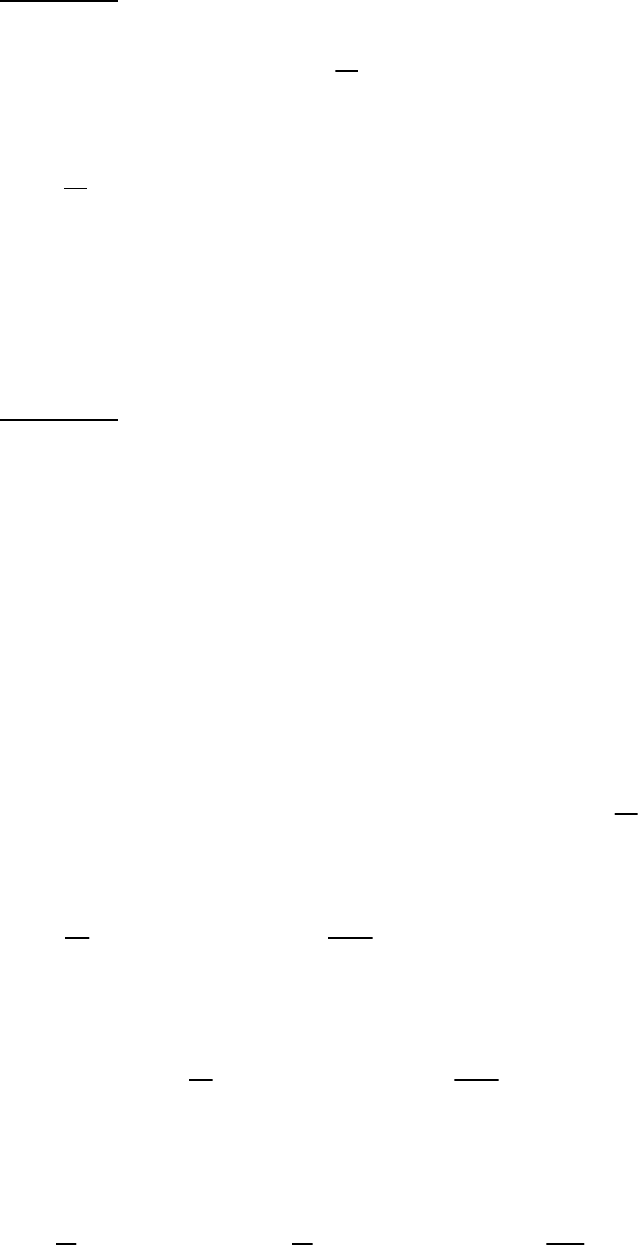
70
Решение.
=+⋅−=⋅
∫∫
++
)2cos3(
3
1
sin
2cos32cos3
xdexdxe
xx
,
3
1
2cos3
ce
x
+−=
+
так как
∫
+= ,cedue
uu
где
.2cos3 +
=
xu
6.2.
(а)
∫
⋅− .5sin)7( xdxx
Решение.
Интеграл вида
∫
Φ xdxx
n
α
sin)(
берется по частям, так как
подынтегральная функция представляет собой произведение алгебраической
функции на трансцендентную, то есть по формуле:
∫∫
−= .vduuvudv
∫
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
−=
=
=
−=
=−
xv
dxdu
xdxdv
xu
xdxx
5cos
5
1
,5sin
,7
5sin)7(
.5sin
25
1
5cos)7(
5
1
cxxx ++−−=
Проверка:
=
′
⎥
⎦
⎤
⎢
⎣
⎡
++−− cxxx 5sin
25
1
5cos)7(
5
1
=
′
+⋅+
′
−−
′
−−= cxxxxx 5cos5
25
1
)5)(cos7(
5
1
5cos)7(
5
1
