Циценкова Г.А., Чукавина Т.В., Рязанова Л.Д., Труппова В.А. Методические указания и контрольные задания по высшей математике
Подождите немного. Документ загружается.

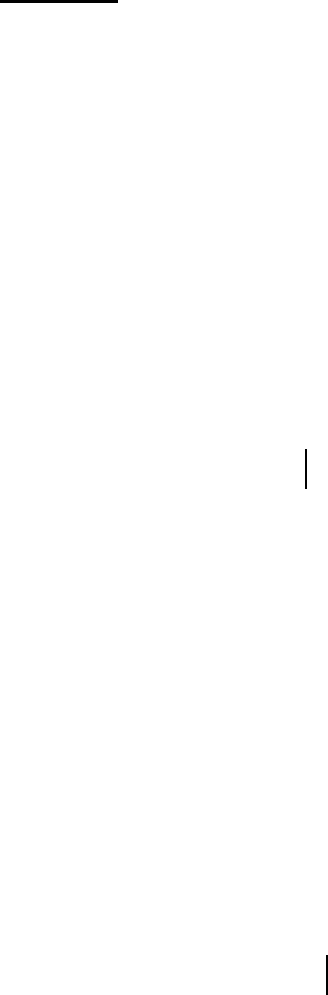
41
⎪
⎩
⎪
⎨
⎧
≥
<<
≤
+−
+
+
=
.2
;20
;0
,4
,)1(
,1
)(
2
x
x
x
x
x
x
xf
Найти точки разрыва, если они существуют. Сделать чертеж.
Решение.
Данная функция задана для
),(
+
∞
−
∞∈x
различными аналитическими
выражениями для соответствующих областей изменения аргумента, такая
функция является неэлементарной, кусочно-заданной [10]. Каждая составляющая
функция является непрерывной функцией на отрезке, где она определена
(
4,1
+
−=+= xyxy
- линейные,
2
)1( += xy
- квадратная) [10]: поэтому
данная функция может иметь разрыв только в трех точках, где меняется ее
аналитическое выражение, то есть в точках х
1
=0, х
2
=2.
1)
х
1
=0. Проверим выполнение трех условий непрерывности:
а)
.010)1()0()(
0
1
=+=+==
=x
xfxf
б)
()
.1)10()1(limlim
;110)1(lim)(lim
22
0
0
0
0
)0(
0
=+=+=
=+=+=
→
>
+→
→
<
−→
xxf
xxf
x
x
x
x
x
x
в)
.1)0()(lim)(lim
00
=
==
+→−→
fxfxf
xx
Итак, функция непрерывна в точке х
1
=0, так как все три условия непрерывности
выполнены.
2)
х
2
=2.
а)
;242)4()2()(
2
2
=+−=+−==
=x
xfxf
б)
;9)12()1(lim)(lim
22
2
)2(
02
=+=+=
→
<
−→
xxf
x
x
x
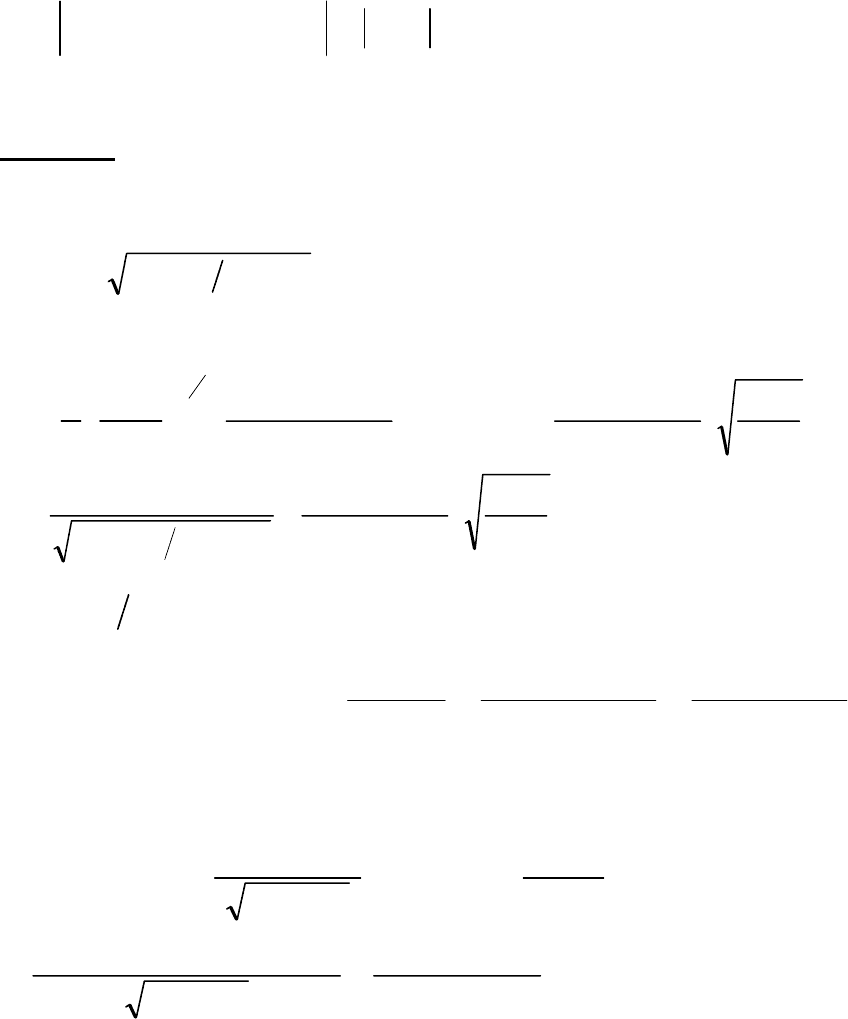
42
в)
.242)4(lim)(lim
2
)2(
02
=
+
−=+
−
=
→
>
+→
xxf
x
x
x
Третье условие непрерывности не выполнено, функция в точке х
2
=2 терпит
разрыв I рода, так как односторонние пределы существуют, но не равны между
собой. Функция в этой точке делает скачок [10]:
.729)(lim)(lim
0202
=−=−=
+→−→
xfxf
xx
δ
Задача 8.
Найти производные
y
′
от данных функций [7].
8.1.
).43()2()5(
7
−⋅−+= xctgxxy
.
2
5
)43(sin
3
)2()5(
)43(
2
5
)43(sin
31
)43(
)2(
)5(2
2
5
7
1
7
2
7
66
7
22
7
6
−
+
⋅
−
−
−+
−
−=
=
−
+
⋅
−
⋅
−−
−
+−−
⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
+
=
′
−
x
x
x
xx
xctg
x
x
x
xctg
x
xx
x
x
y
8.2.
.71
3
xtgy =
()
.
7sin
7cos21
7cos7
21
7cos
7
737
4
2
242
43
x
x
xxtgx
xtgxtgy
−
=
−
=⋅−=
′
=
′
−−
8.3.
).5ln(4arcsin
25
−⋅= xxy
.
5
4arcsin2
161
)5ln(4arcsin20
5
2
4arcsin
161
)5ln(4
4arcsin5
2
5
2
24
2
5
2
2
4
−
+
−
−⋅
=
=
−
+
−
−
=
′
x
xx
x
xx
x
x
x
x
x
xy
8.4.
.7cos3
3
4
xy
x
⋅=
−

43
.7sin3217cos33ln4
21)7sin(37cos)4(3ln3
2333
2333
44
44
xxxx
xxxxy
xx
xx
⋅⋅−⋅⋅−=
=⋅−+−⋅=
′
−−
−−
8.5.
.41 xarctgy −=
.
41)21(
1
41)42(
2
412
4
)41(1
1
2
xxxxxx
y
−−
−=
−−
−=
−
−
⋅
−+
=
′
8.6.
()
.7sin
)53( −
=
xarcctg
xy
Прологарифмируем обе части равенства [7].
),7ln(sin)53(ln xxarcctgy ⋅−=
имеем:
.7cos7
7sin
1
)53()7ln(sin3
)53(1
1
2
x
x
xarcctgx
xy
y
⋅⋅−+⋅
−+
−=
′
Отсюда:
.
7sin
7cos)53(7
)53(1
)7ln(sin3
)7(sin
2
)53(
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
−+
−
=
′
−
x
xxarcctg
x
x
xy
xarcctg
8.7.
.sin
22
yyx =+
Данное равенство определяет неявную функцию у аргумента Х [7]. Находим
производную от левой и правой части данного равенства:
.cos22 yyyyx
′
⋅
=
′
⋅+
Решаем полученное уравнение относительно
y
′
:
,2)cos2(
,2cos2
xyyy
xyyyy
−=−
′
−
=
′
⋅−
′
откуда имеем:
.
cos2
2
yy
x
y
−
−
=
′
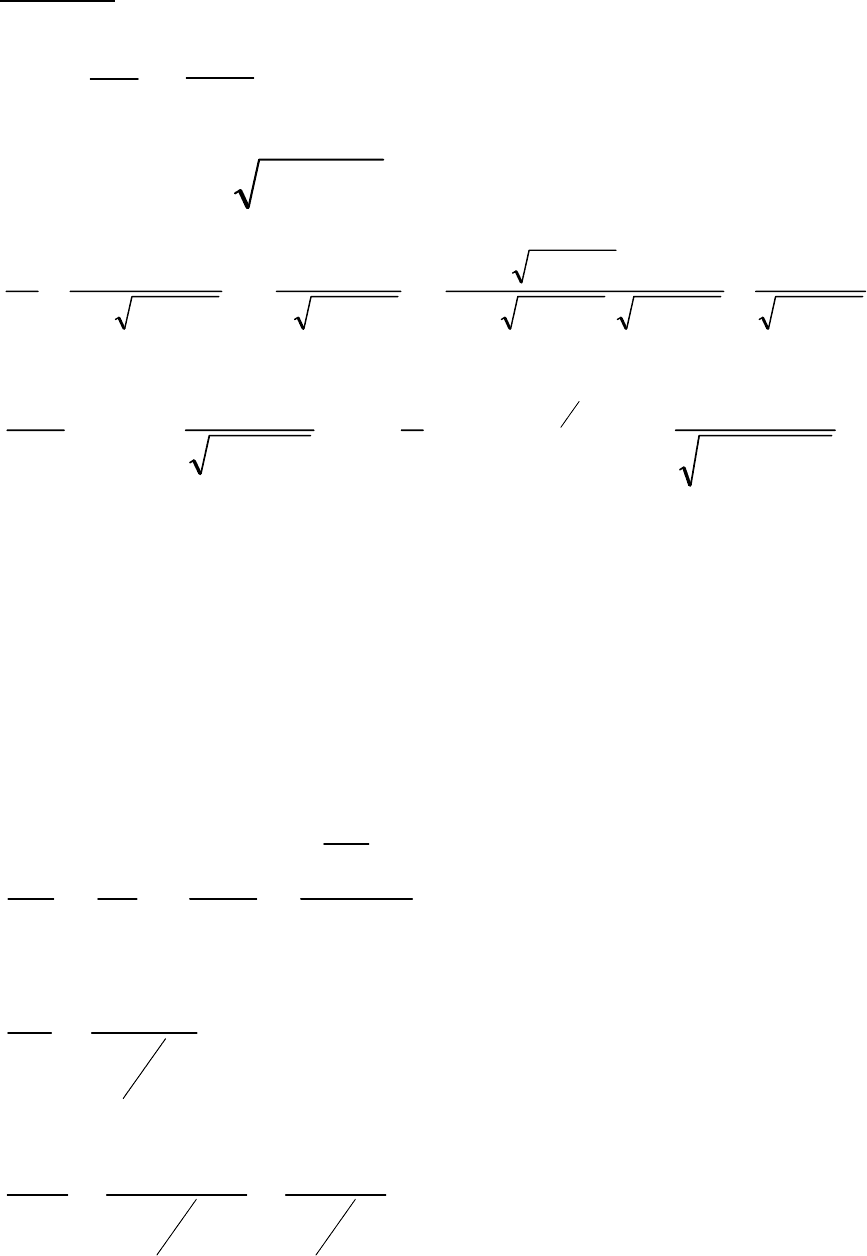
44
Задача 9.
Найти
dx
dy
и
2
2
dx
yd
для заданных функций.
9.1.
).ln(
22
axxy ++=
.
1
)(2
2
1
1
222222
22
2222
axaxaxx
xax
ax
x
axx
dx
dy
+
=
+++
++
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
++
=
()
.2)(
2
11
3
22
2
3
22
22
2
2
ax
x
xax
ax
y
dx
yd
+
−
=⋅+−=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=
′′
=
−
9.2.
⎩
⎨
⎧
++=
=
.12
,ln
3
tty
tx
Данная функция задана параметрическими уравнениями. Первую и вторую
производные находим по формулам [4].
.;
2
2
t
t
t
t
x
dx
dy
dx
yd
x
y
dx
dy
′
′
⎟
⎠
⎞
⎜
⎝
⎛
=
′
′
=
.23
1
23
3
2
tt
t
t
dx
dy
+=
+
=
()
.29
1
29
1
23
3
23
2
2
tt
t
t
t
tt
dx
yd
+=
+
=
′
+
=

45
Задача 10.
Найти наибольшее и наименьшее значение функции
13)(
23
+−= xxxf
на отрезке [-1;4].
На отрезке функция
)(xfy =
может достигать наименьшего (У
наим.
) или
наибольшего (У
наиб..
) значения либо в критических точках функции, лежащих в
интервале (a;b) либо на концах отрезка [a;b] [7].
Найдем критические точки данной функции на отрезке [-1;4]. Для этого находим
производную этой функции и приравниваем ее нулю [7].
.2,0,0)2(,063,63
21
22
===−=−−=
′
xxxxxxxxy
Точки
0
1
=x
и
2
2
=
x
принадлежат интервалу [-1;4]. Вычисляем значения
функции в критических точках и концах отрезка:
.17)4(;3)1(;3)2(;1)0(
=
−
=
−−== yyyy
Сравнивая, полученные значения, заключаем, что У
наим.
.=-3, в точках
2
2
=
x
и
1−=x
, У
наиб.
=17, в точке х=b=4.
Ответ:
На отрезке [-1;4] У
наим.
=-3; У
наиб.
=17.
Задача 11.
Исследовать методами дифференциального исчисления функцию
2
3
4
x
x
y
+
=
и,
используя результаты исследования, построить ее график [7].
Исследование функции можно провести по следующей схеме [7]:
Найти область определения функции.
Исследовать на непрерывность, найти точки разрыва графика функции.
Найти уравнения вертикальных, наклонных асимптот, если они существуют.
Найти интервалы монотонности, точки экстремума функции.
Найти интервалы выпуклости, вогнутости графика функции, точки перегиба.
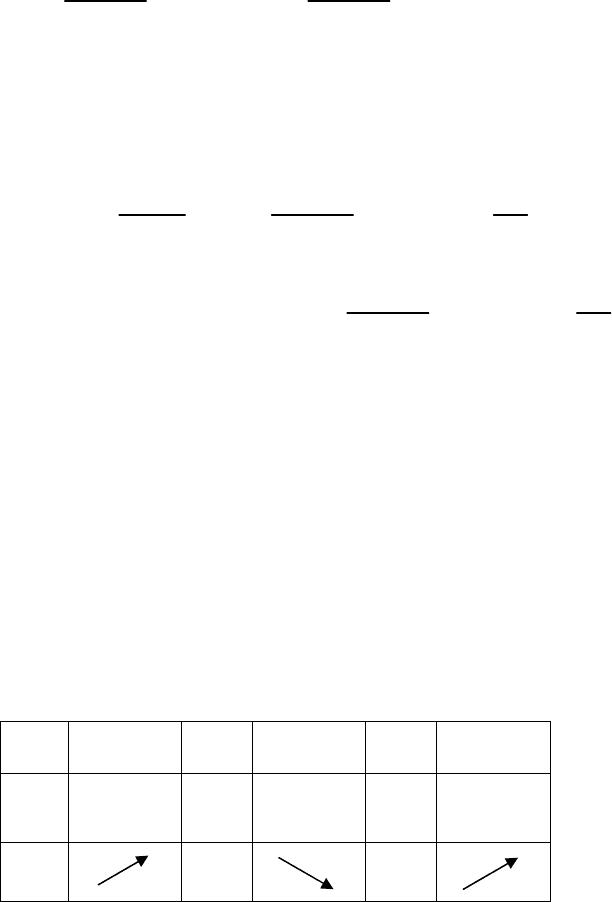
46
Выяснить четность, нечетность, периодичность функции.
Найти, если несложно, точки пересечения с осями координат, выяснить поведение
функции в бесконечно удаленной точке.
Построить график функции, используя результаты исследования.
Данная функция существует всюду, кроме точки Х=0, т.е. на интервалах (-
∞, 0)
(0,+
∞). Точка Х=0 является точкой разрыва второго рода, так как
+∞=
+
+∞=
+
−→+→
2
3
0
2
3
0
4
lim;
4
lim
x
x
x
x
xx
,
поэтому прямая
0=x является вертикальной асимптотой.
Наклонная асимптота имеет уравнение
bkxy
+
=
, где
[]
.0
4
lim
4
lim)(lim
,1
4
1lim
4
lim
)(
lim
32
3
33
3
==
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=−=
=
⎟
⎠
⎞
⎜
⎝
⎛
+=
+
==
±∞→±∞→±∞→
±∞→±∞→±∞→
x
x
x
x
kxxfb
xx
x
x
xf
k
xxx
xxx
Уравнение наклонной асимптоты: у=х. Исследуем функцию на экстремум.
Точками экстремума могут быть точки, в которых
0
=
′
y
либо
∞=
′
y
.
./)8(/)823(
33444
xxxxxxy −=−−=
′
0=
′
y
при Х=2;
∞
=
′
y
при Х=0.
Имеем одну критичесую точку Х=2, так как Х=0 не принадлежит области
определения функции.
х
(-
∞, 0)
0 (0,2) 2
(2,+∞)
y
′
+
∞
- 0 +
y
∞
3
Y
min
(2)=3.
Функция возрастает на интервалах (-
∞, 0) и (2,+∞), убывает на интервале (0,2).
Точками перегиба могут быть точки, в которых
0
=
′
′
y
либо
∞=
′′
y
.

47
()
.0;0
.
24
81
8
1
8
4
3
33
3
=∞=
′′
≠
′′
=
′
−=
′
⎟
⎠
⎞
⎜
⎝
⎛
−=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
′′
−
xприyy
x
x
xx
x
y
Так как х=0 не принадлежит области определения функции, поэтому точек
перегиба нет
Х
(-
∞, 0)
0
(0,+∞)
y
′′
+
∞
+
y
∪
∞
∪
Кривая всюду вогнута.
Функция называется четной, если она удовлетворяет равенству
)()( xfxf =−
, и
нечетной, если
)()( xfxf −=−
. Данная функция не является четной, ни
нечетной. График функции пересекает ось ОХ в точке
)0,4(
3
−
.

48
Контрольная работа № 2.
Раздел 1. Дифференциальное исчисление
функций нескольких переменных
Вопросы для самоподготовки
1. Функция двух, трех переменных (определение, область определения).
Геометрическое толкование функции 2-х переменных.
2.
Линия уровня функции 2-х переменных, их геометрическая
интерпретация. Поверхности уровня функции трех переменных.
3.
Предел функции 2-х переменных в точке. Непрерывность функции в
точке.
4.
Понятие частного и полного приращения функции двух переменных.
Определение частных производных, их геометрическая интерпретация.
5.
Полный дифференциал и его связь с частными производными.
Применение полного дифференциала для вычисления приближенного
значения функции.
6.
Уравнение касательной плоскости и нормали к поверхности в данной
точке.
7.
Понятие сложной функции двух промежуточных аргументов и двух
независимых переменных. Формулы частных производных сложной
функции по независимым переменным:
(
)
vufz ,
=
;
(
)
yxu ,
ϕ
=
;
()
yxv ,
ψ
=
;
x
z
∂
∂
и
y
z
∂
∂
.
8.
Сложная функция двух, трех промежуточных аргументов, одной
независимой переменной. Формулы для нахождения полной
производной:
dx
dz
, если
а)
()
vufz ,=
,
(
)
xu
ϕ
=
и
(
)
xv
ψ
=
;

49
б)
()
vuxfz ,,=
,
(
)
xu
ϕ
=
и
(
)
xv
ψ
=
.
9. Формула производной неявной функции
(
)
xfy
=
, заданной
уравнением
()
0, =yxF
.
10. Формулы частных производных неявной функции, заданной уравнением
()
0,,
=
zyxF
.
11. Частные производные высших порядков. Теорема о равенстве смешанных
частных производных функций двух переменных.
12.
Понятие скалярного поля (на плоскости и в пространстве). Производная
скалярного поля
(
)
zyxuu ,,=
в данной точке
()
0000
,, zyxM
по
направлению вектора
a
. Формула ее вычисления. Механический смысл.
13.
Градиент скалярного поля
(
)
zyxuu ,,
=
в данной точке
()
0000
,, zyxM
. Связь между производной по направлению и
градиентом. Свойства градиента. Механический смысл градиента.
14.
Определение максимума и минимума функции двух переменных.
Необходимые и достаточные условия существования экстремума функции
двух переменных. Правила нахождения экстремумов.
15.
Понятие аппроксимирующей функции для функций, заданных таблично.
Метод наименьших квадратов нахождения коэффициентов
аппроксимирующей функции.
Контрольные задания
Задача 1.
1.1. Дана функция
522
)( yx
y
z
−
=
. Показать, что
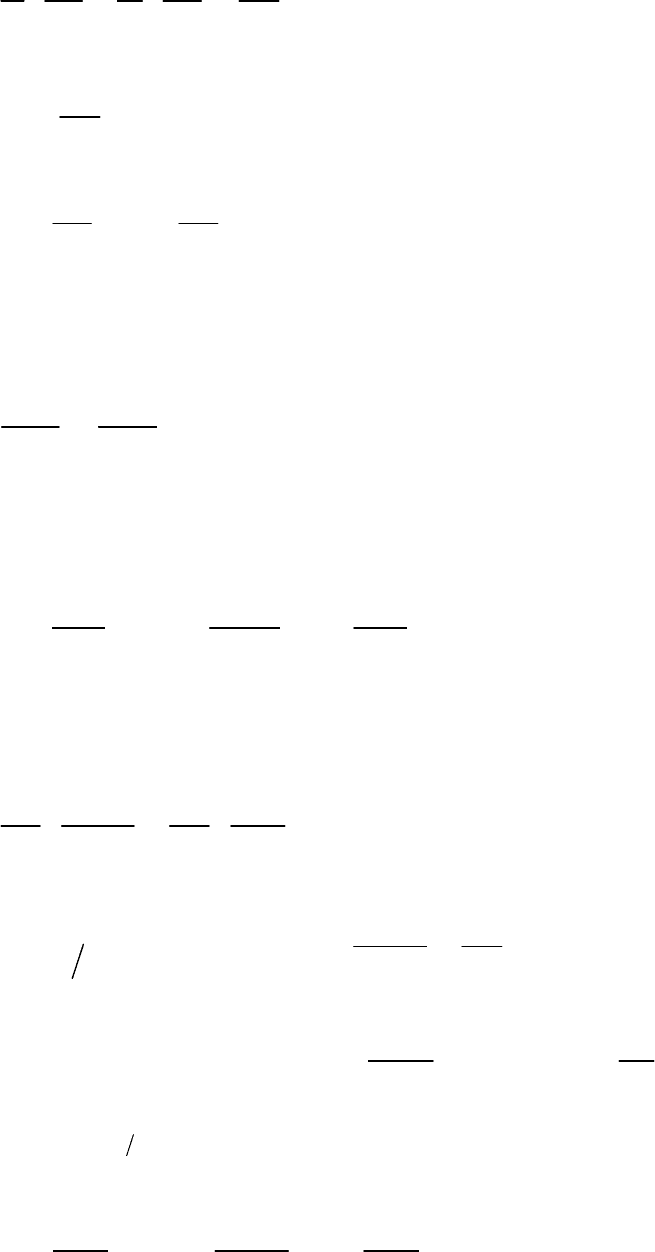
50
2
11
y
z
y
z
yx
z
x
=
∂
∂
⋅+
∂
∂
⋅
.
1.2. Дана функция
)arcsin(
3
2
xy
x
y
z +=
. Показать, что
0
22
=+
∂
∂
⋅−
∂
∂
⋅ y
y
z
xy
x
z
x
.
1.3. Дана функция
)12ln(
22
+++= xyxz
. Показать, что
0
2
2
2
2
=
∂
∂
+
∂
∂
y
z
x
z
.
1.4. Дана функция
xy
ez =
. Показать, что
022
2
2
2
2
2
2
2
=+
∂
∂
+
∂∂
∂
⋅−
∂
∂
⋅ xyz
y
z
y
yx
z
xy
x
z
x
.
1.5. Дана функция
)ln(
y
exz
−
+=
. Показать, что
0
2
22
=
∂
∂
⋅
∂
∂
−
∂∂
∂
⋅
∂
∂
x
z
y
z
yx
z
x
z
.
1.6. Дана функция
yxz =
. Показать, что
0
2
=
∂
∂
−
∂∂
∂
y
z
yx
z
x
.
1.7. Дана функция
y
xz =
. Показать, что
x
z
xy
yx
z
y
∂
∂
⋅+=
∂∂
∂
⋅ )ln1(
2
.
1.8. Дана функция
xy
xez =
. Показать, что
02
2
2
2
2
2
2
2
=
∂
∂
+
∂∂
∂
⋅+
∂
∂
⋅
y
z
y
yx
z
xy
x
z
x
.
