Циценкова Г.А., Чукавина Т.В., Рязанова Л.Д., Труппова В.А. Методические указания и контрольные задания по высшей математике
Подождите немного. Документ загружается.

51
1.9. Дана функция
)sin( ayxz
+
=
. Показать, что
2
2
2
2
2
x
z
a
y
z
∂
∂
=
∂
∂
.
1.10. Дана функция
yxyyz sin)(cos
−
+
=
. Показать, что
y
z
yx
z
yx
∂
∂
=
∂⋅∂
∂
−
2
)(
.
Задача 2.
Дана функция
),( yxfz =
и две точки
),(
00
yxA
и
),(
11
yxB
.
Требуется : 1) вычислить значение
1
z
функции в точке
B
; 2) вычислить
приближенное значение
1
~
z
функции в точке
B
, исходя из значения функции
0
z
в
точке
A
, заменив приращение функции при переходе от точки
A
к точке
B
дифференциалом, и оценить в процентах относительную погрешность,
возникшую при замене приращения функции ее дифференциалом; 3) составить
уравнение касательной плоскости к поверхности
),( yxfz
=
в точке
),,(
000
zyxC
.
2.1.
22
yxyxz ++=
;
)2,1(A
,
)96,1;02,1(B
.
2.2.
yxxyxz ++−=
2
3
;
)3,1(A
,
)92,2;06,1(B
.
2.3.
yxyxz 63
2
−+=
;
)1,4(A
,
)03,1;96,3(B
.
2.4.
yxyxz 36
22
++−=
;
)3,2(A
,
)97,2;02,2(B
.
2.5.
22
32 yxyxz ++=
;
)1,2(A
,
)04,1;96,1(B
.
2.6.
12
22
−+++= yxyxz
;
)4,2(A
,
)91,3;98,1(B
.
2.7.
xyyxz −+=
22
23
;
)3,1(
−
A
,
)97,2;98,0(−B
.

52
2.8.
yxyxz 45
22
++−=
;
)2,3(A
,
)98,1;05,3(B
.
2.9.
xyxyz 532
2
−+=
;
)4,3(A
,
)95,3;04,3(B
.
2.10.
xyxyz 22
2
−+=
;
)2,1(A
,
)03,2;97,0(B
.
Задача 3.
Исследовать на экстремум функцию
),( yxfz
=
.
3.1.
568
33
+−+= xyyxz
.
3.2.
22
22151 yxyxxz −−−+=
.
3.3.
22
61 yxyxxz −−−+=
.
3.4.
2018396
23
++−−+= yxxyyxz
.
3.5.
5622
33
+−+= xyyxz
.
3.6.
10933
33
+−+= xyyxz
.
3.7.
1
22
+−+++= yxyxyxz
.
3.8.
22
)(4 yxyxz −−−=
.
3.9.
22
33)(6 yxyxz −−−=
.
3.10.
yxyxyxz 96
22
−−++=
.
Задача 4.
Дано скалярное поле, определяемое функцией
),( yxfz
=
, и точки
),(
111
yxA
и
),(
222
yxA
. Найти скорость изменения скалярного поля
),( yxfz =
в направлении вектора
21
AA
. Найти
zgrad
и наибольшую
скорость изменения поля
z
в точке
1
A
.
53
4.1.
;
22
yxyxz ++=
)1;1(
1
A
)2;3(
2
−
A
4.2.
;32
22
yxyxz ++=
)1;2(
1
A
)1;4(
2
A
4.3.
);35ln(
22
yxz +=
)1;1(
1
A
)3;2(
2
−
A
4.4.
;24
22
xyyxz ++=
)1;1(
1
A
)4;3(
2
A
4.5.
;65
2
xyxz +=
)1;2(
1
A
)2;3(
2
A
4.6.
);(
2
xyarctgz =
)3;2(
1
A
)1;3(
2
−
A
4.7.
);arcsin(
2
yxz =
)2;1(
1
A
)5;2(
2
A
4.8.
);43ln(
22
yxz +=
)3;1(
1
A
)2;3(
2
A
4.9.
;23
324
yxxz +=
)2;1(
1
−
A
)1;2(
2
A
4.10.
;53
222
xyyxz +=
)1;1(
1
A
)0;3(
2
A
Задача 5.
Экспериментально получены пять значений искомой функции
)(xfy =
при
пяти значениях аргумента, которые записаны в таблице. Методом наименьших
квадратов найти аппроксимирующую функцию
)(xfy
=
в виде линейной
функции
baxy +=
.
x
1 2 3 4 5 5.1.
y
4.3 5.3 3.8 1.8 2.3
x
1 2 3 4 5 5.2.
y
4.5 5.5 4.0 2.0 2.5
x
1 2 3 4 5 5.3.
y
4.7 5.7 4.2 2.2 2.7
x
1 2 3 4 5 5.4.
y
4.9 5.9 4.4 2.4 2.9
54
x
1 2 3 4 5 5.5.
y
5.1 6.1 4.6 2.6 3.1
x
1 2 3 4 5 5.6.
y
3.9 4.9 3.4 1.4 1.9
x
1 2 3 4 5 5.7.
y
5.2 6.2 4.7 2.7 3.2
x
1 2 3 4 5 5.8.
y
5.5 6.5 5.0 3.0 3.5
x
1 2 3 4 5 5.9.
y
5.7 6.7 5.2 3.2 3.7
x
1 2 3 4 5 5.10.
y
5.9 6.9 5.4 3.4 3.9
Решение типового варианта
Задача 1.
1.1. дана функция
.53
223
yyxxZ −−=
Найти частные производные первого и
второго порядка. Доказать, что смешанные производные равны.
Решение.
xyx
x
z
109
2
−=
∂
∂
(производная по х найдена в предположении, что у – постоянная
величина в момент дифференцирования).
yx
y
z
25
2
−−=
∂
∂
(производная по у найдена в предположении, что х – величина
постоянная в момент дифференцирования) [10].
55
.
;10
;2
;10
;1018
22
2
2
2
2
2
2
xy
z
yx
z
x
x
z
yxy
z
y
z
yy
z
x
y
z
xyx
z
yx
x
z
xx
z
∂∂
∂
=
∂∂
∂
−=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
∂∂
∂
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
=
∂
∂
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
=
∂∂
∂
−=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
∂
∂
1.2. Проверить, что функция
zy
yx
xW
−
−
+=
удовлетворяет уравнению
.1=
∂
∂
+
∂
∂
+
∂
∂
z
w
y
w
x
w
Решение.
Находим
,
1
1
zyx
w
−
+=
∂
∂
(y , z – постоянные).
222
)()()(
)()()()(
zy
xz
zy
xyyz
zy
yxzyzyyx
y
w
−
−
=
−
−
+
−
=
−
−
′
−
−
−
′
−
=
∂
∂
(x, z – постоянные).
22
)(
)1(
)(
1
)(
zy
yx
zy
yx
z
w
−
−
=−⋅
−
⋅−−=
∂
∂
(x, y – постоянные).
Подставим найденные производные в данное уравнение:
.1
)(
)(
)(
)(
)()(
1
1
2
2
2
2
22
=
−
−
=
−
−+−+−+−
=
=
−
−
+
−
−
+
−
+=
∂
∂
+
∂
∂
+
∂
∂
zy
zy
zy
yxxzzyzy
zy
yx
zy
xz
zyz
w
y
w
x
w
Задача 2.
Дана функция
xxyxZ 223
3
−+=
и две точки А(2; 3) и В(1,98; 3,04).
Требуется:
56
1) вычислить значение
1
z
в точке В; 2) вычислить приближенное значение
1
~
z
функции в точке
В, исходя из значения
0
z
функции в точке А, заменив
приращение функции при переходе от точки
А к точке В дифференциалом; 3)
оценить в процентах относительную погрешность, получающуюся при замене
приращения функции ее дифференциалом; 4) составить уравнение касательной
плоскости и нормали к поверхности
),( yxfz
=
в точке С(2; 3;
0
z
).
Решение.
,04,0,02,0;04,3;98,1
00
=
∆
−
=
∆
=
∆+==∆+= yxyyyxxx
так как
.322232223)3;2()(;3;2
3
000
=⋅−⋅⋅+⋅===== fAzzyx
1)
.3656,3198,1204,398,12)98,1(3)(
~
3
1
=⋅−⋅⋅+=Bz
2)
.),()(
~
),(
01
00
yx
o
dzyxfBz +=
.36,3104,04)02,0(4032)(
~
.4)3;2(
.40)3;2(
;2
;229
.),(),(
1
2
0000
),(
00
=⋅+−⋅+=
=
′
=
′
=
′
−+=
′
∆
′
+∆
′
=
Bz
f
f
xf
yxf
yyxfxyxfdz
y
x
y
x
yx
yx
3) относительная погрешность вычисляется по формуле
%.018,0%100
36,31
3656,3136,31
%100
~
~
1
11
=⋅
−
=⋅
−
=
z
zz
δ
4) запишем уравнения касательной плоскости и нормали к поверхности
),( yxfz =
в точке
),,(
000
zyx
соответственно [13]:
.
1),(),(
;0)()(),()(),(
0
00
0
00
0
0000000
−
−
=
′
−
=
′
−
=−−−⋅
′
+−⋅
′
zz
yxf
yy
yxf
xx
zzyyyxfxxyxf
yx
yx
57
Для нашей задачи эти уравнения примут вид:
.0)32()3(4)2(40
=
−−−
+
−
zyx
или
060440 =−−+ zyx
- уравнение касательной плоскости;
1
32
4
3
40
2
−
−
=
−
=
− zyx
- уравнение нормали к заданной поверхности в точке
(2, 3, 32).
Задача 3.
Исследовать на экстремум функцию
.3
33
xyyxz −+=
Решение задачи состоит из трех частей.
1.
С помощью необходимого условия существования экстремума, то есть из
системы
⎩
⎨
⎧
=
′
=
′
,0),(
,0),(
yxz
yxz
y
x
найдем координаты стационарных (критических) точек [10].
2.
Проверим выполнение достаточного условия существования экстремума в
каждой из стационарных точек. Для этого составим
,
2
BAC −=∆
где
00
0
;;
M
yy
M
xy
M
xx
zCzBzA
′′
=
′′
=
′′
=
и вычислим значение
∆
в каждой стационарной точке. Те стационарные точки, в
которых значение
0>∆
, будут являться точками экстремума.
3.
Решим вопрос о характере экстремума. Точка
),(
000
yxM
будет точкой
максимума, если
0)(
0
<MA
, и точкой минимума, если
.0)(
0
>MA
Решение.
Для заданной функции
x
z
′
и
y
z
′
всегда существуют и для нахождения
стационарных точек запишем систему уравнеий:
⎪
⎩
⎪
⎨
⎧
=−=
′
=−=
′
033
,033
2
2
xyz
yxz
y
x
или
⎩
⎨
⎧
=−
=−
.0
,0
2
2
xy
yx

58
Решение системы:
.1;0;1;0
2121
=
=
=
= yyxx
Получаем две
стационарные точки
)0,0(
1
M
и
)1,1(
2
M
.
Найдем:
.6;3;6
2
22
2
2
y
y
z
C
yx
z
BAx
x
z
=
∂
∂
=−=
∂∂
∂
===
∂
∂
Составим
.936
2
−=−=∆ xyBAC
Вычислим
∆
в точке
);0,0(
1
M
то есть
(
)
.09
1
<
−
=
∆
M
Делаем вывод, что в
точке
1
M
экстремума нет. Значение
(
)
,027
2
>
=
∆
M
следовательно в точке
2
M
экстремум есть, причем точка
2
M
является точкой минимума, так как
()
.06
2
>=MA
.1)(
2min
−== MZZ
Задача 4.
Найти скорость изменения скалярного поля, определяемого функцией
)ln(
22
yxZ +=
в точке
)3,1(
1
A
в направлении вектора
21
AA
, если точка
)6,3(
2
A
. Найти
dzgra
в точке
1
A
и наибольшую скорость изменения поля в
этой точке.
Решение.
Скорость изменения поля в заданном направлении есть производная скалярного
поля
),( yxfz =
по направлению вектора
21
AA
, задающего направление.
Обозначим
,
21
aAA
=
тогда
,cos),(cos),(
0000
),(
00
βα
⋅
′
+⋅
′
=
∂
∂
yxfyxf
a
z
yx
yx
где
α
cos
и
β
cos
- направляющие косинусы вектора
).,( yxa
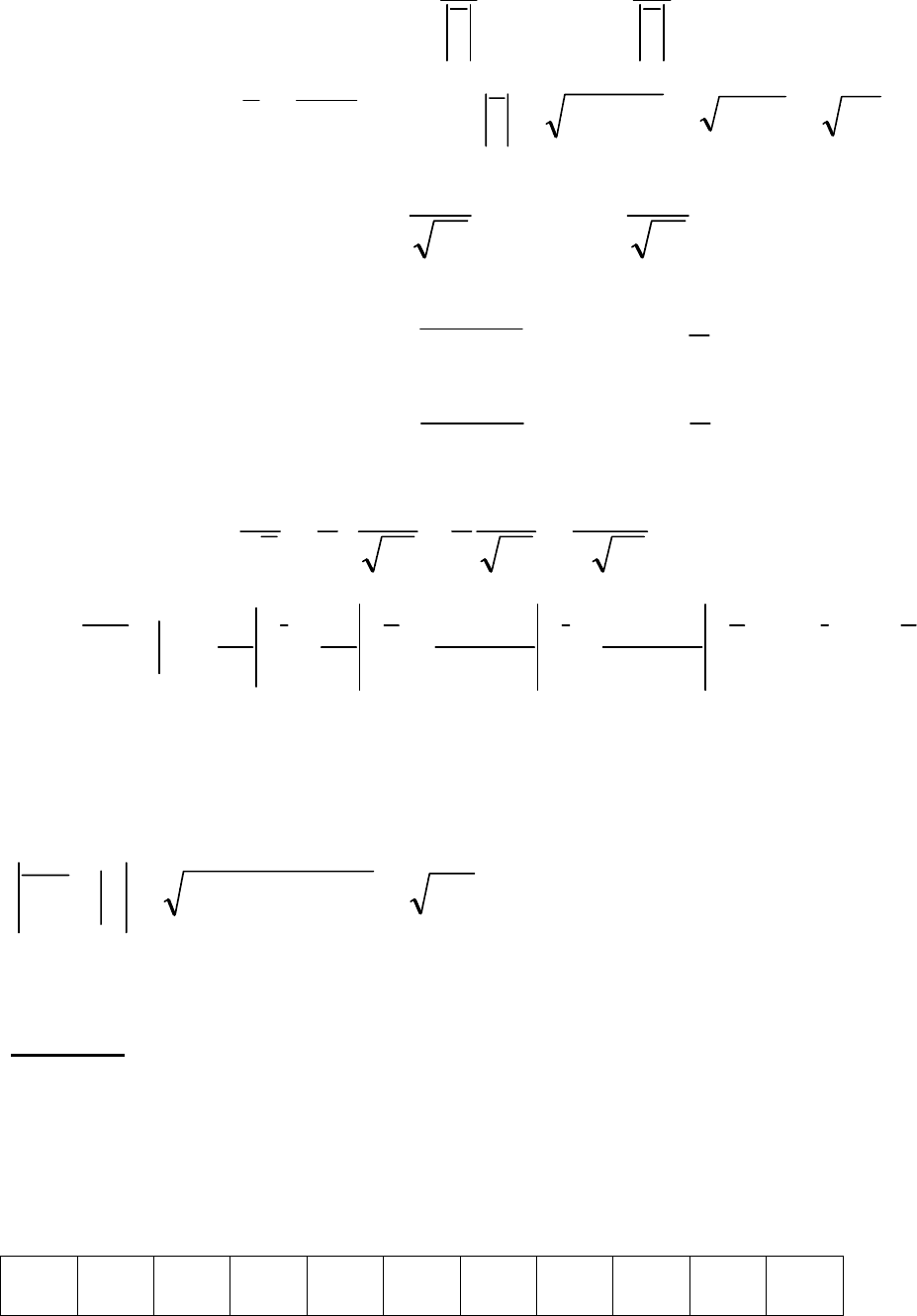
59
a
a
a
a
y
x
==
βα
cos;cos
Находим:
);3;2(
21
== AAa
;1394
22
=+=+= yxa
;
13
3
cos;
13
2
cos ==
βα
;
5
3
)3;1(
;
5
1
)3;1(
;
2
),(
;
2
),(
22
22
=
′
=
′
+
=
′
+
=
′
y
x
y
x
f
f
yx
y
yxf
yx
x
yxf
.611,0
135
11
13
3
5
3
13
2
5
1
≈=+⋅=
∂
∂
a
z
.6,02,0
22
111
1
1
2222
jij
yx
y
i
yx
x
j
y
z
i
x
z
dzgra
AAA
A
A
+=
+
+
+
=
∂
∂
+
∂
∂
=
Наибольшая скорость изменения поля в точке
),(
00
yx
равна модулю градиента в
точке
),(
00
yx
.
632,04,0)6,0()2,0(
22
1
≈=+=
A
dzgra
- величина наибольшей скорости
заданного скалярного поля в точке
1
A
.
Задача 5.
Экспериментально получены значения искомой функции
),(xfy =
которые
записаны в таблицу. Методом наименьших квадратов найти функцию
)(xfy =
в виде
.baxy
+
=
i
x
15 18 21 24 27 30 33 36 39 42

60
i
y
4,5 5,2 5,8 6,3 7,0 7,7 8,3 8,8 9,5 10
Решение.
Если по данным таблицы построить точки, то по чертежу увидим, что точки
располагаются вдоль прямой. Поэтому аппроксимирующую функцию будем
искать в виде
.baxy +=
Для определения коэффициентов
a
и
b
в
соответствии с методом наименьших квадратов составляем систему уравнений:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
==+
=+
∑∑
∑∑∑
==
===
.10,1,
,
11
111
2
iynbxa
yxxbxa
n
i
n
i
ii
n
i
n
i
iii
n
i
i
Для удобства вычислений сумм составим таблицу.
i
i
x
i
y
2
i
x
ii
yx
1 15 4,5 225 67,5
2 18 5,2 324 93,6
3 21 5,8 441 121,8
4 24 6,3 576 151,2
5 27 7,0 729 189,0
6 30 7,7 900 231,0
7 33 8,3 1089 273,9
8 36 8,8 1296 316,8
9 39 9,5 1521 370,5
10 42 10,0 1764 420,0
∑
285 73,1 8865 2235,3
Составим систему уравнений:
