Циценкова Г.А., Чукавина Т.В., Рязанова Л.Д., Труппова В.А. Методические указания и контрольные задания по высшей математике
Подождите немного. Документ загружается.

11
4.7.
⎪
⎩
⎪
⎨
⎧
=−+
=−+
=−+
.334
,2638
,1
321
321
321
xxx
xxx
xxx
4.8.
⎪
⎩
⎪
⎨
⎧
−=−−
=++
−=−−
.9653
,53
,324
321
321
321
xxx
xxx
xxx
4.9.
⎪
⎩
⎪
⎨
⎧
−=++
−=+
=−
.20432
,43114
,3157
321
31
21
xxx
xx
xx
4.10.
⎪
⎩
⎪
⎨
⎧
=+−
=++
=++
.93
,2025
,3142
321
321
321
xxx
xxx
xxx
Задача 5.
Дано комплексное число Z. Требуется: 1) записать число Z в
алгебраической и тригонометрической формах; 2) найти все корни
уравнения
0
3
=Ζ+
ω
.
5.1.
()
iz += 122
. 5.2.
(
)
314 iz +=
.
5.3.
()
iz −−= 122
. 5.4.
(
)
314 iz −−=
.
5.5.
()
iz +−= 122
. 5.6.
(
)
iz −= 122
.
5.7.
(
)
314 iz −=
. 5.8.
(
)
iz −−= 34
.
5.9.
(
)
iz += 31
. 5.10.
(
)
iz −= 31
.
Решение типового варианта
Задача 1.
Даны векторы
()
1;2;3 −a
,
(
)
2;1;1 −−b
,
(
)
3;1;2
−
c
,
(
)
5;6;11 −d
в некотором
базисе. Показать, что векторы
cba ,,
образуют базис и найти координаты
вектора
d
в этом базисе.
12
Решение.
Равенство
cbad
γβα
++=
(1) называется разложением вектора
d
по
векторам
cba ,,
[1]. Нас интересует такие системы векторов, по которым
разложение любого вектора пространства возможно и притом единственным
образом. Такой системой векторов в пространстве служит любая тройка
некомпланарных векторов
cba ,,
, которые называются базисом пространства,
а коэффициенты разложения вектора
d
γ
β
α
,,
- координатами вектора в этом
базисе.
Покажем, что векторы
cba ,,
образуют базис. Смешанное произведение
некомпланарных векторов отлично от нуля [1].
()
08662189
312
211
123
,, ≠=++−−+−=
−
−−
−
=cba
Итак, векторы
cba ,,
образуют базис.
Найдем координаты вектора
d
в этом базисе. Равенство (1) равносильно
системе линейных уравнений с тремя неизвестными
γ
β
α
,,
:
⎪
⎩
⎪
⎨
⎧
=−−
−=++−
=+−
.532
,62
,1123
γβα
γβα
γβα
Решим ее по правилу Крамера [10]:
∆
∆
=
α
α
,
∆
∆
=
β
β
,
∆
∆
=
γ
γ
.

13
Вычислим определитель системы линейных уравнений, который составлен
из коэффициентов при неизвестных:
8662819
321
112
213
=++−+−−=
−−
−
−
=∆
Вычислим вспомогательные определители
γβα
∆
∆
∆
,,
, которые
получаются из определителя системы путем замены столбца коэффициентов при
соответствующей неизвестной столбцом свободных членов:
1618221024533
325
116
2111
=++−+−−=
−−
−
−
=∆
α
,
24661512201154
351
162
2113
−=−−+−++=
−
−−=∆
β
,
836101164415
521
612
1113
=−−−++=
−
−−
−
=∆
γ
,
Решение системы имеет вид:
2
8
16
==
α
;
3
8
24
−=
−
=
β
;
1
8
8
==
γ
.
Итак, вектор
d
в базисе
cba ,,
представим в виде:
cbad +−= 32
, т.е. имеем координаты (2;-3;1).
14
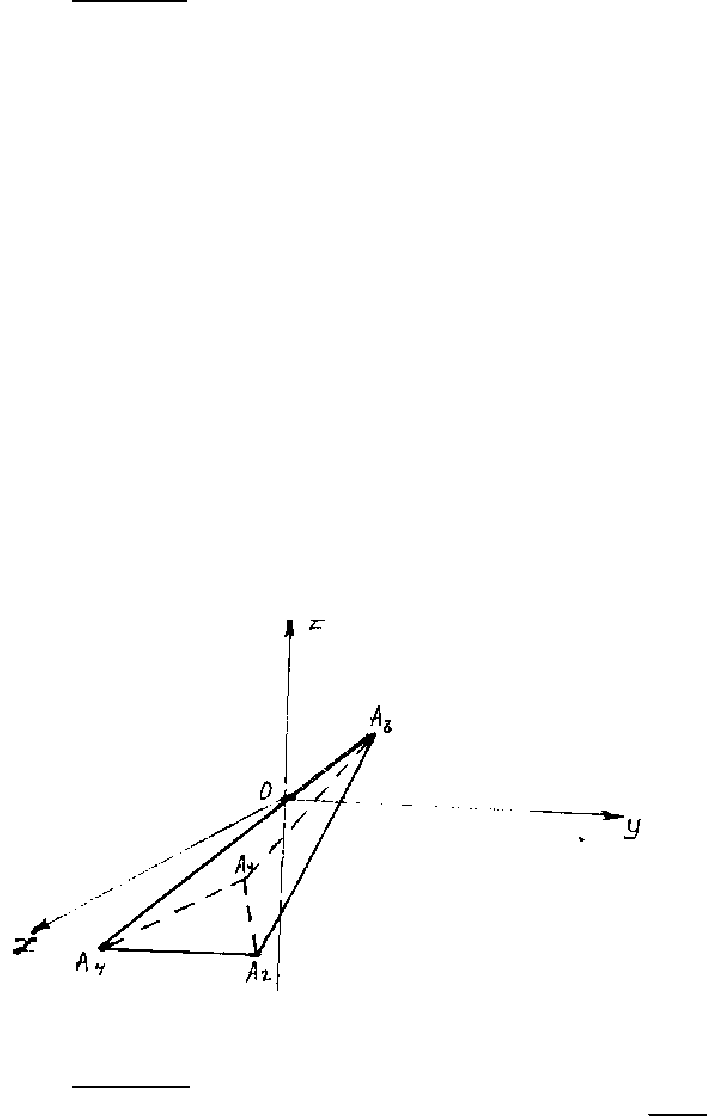
Задача 2.
Даны координаты вершин пирамиды 4321
AAAA
,
)0;1;2(
1
A
,
)1;2;3(
2
−A
,
)2;2;1(
3
A
,
)2;1;2(
4
−
−
A
.
Найти:
1)
длину ребра 21
AA
; 2) угол между ребрами 21
AA
и 41
AA
; 3) площадь грани
321
AAA
; 4) объем пирамиды; 5) уравнение прямой 21
AA
; 6) уравнение
плоскости 321
AAA
; 7) угол между ребром 41
AA
и гранью 321
AAA
; 8) уравнение
высоты, опущенной из вершины
4
A
на грань 321
AAA
.
Решение.
1) Длину ребра 21
AA
найдем как длину вектора 21
AA
по формуле [7]:
15
()()()
)(3)1(11
2
2
12
2
12
2
1221
едzzyyxxAA =−++=−+−+−=
2) Угол между ребрами
21
AA
и 41
AA
найдем как угол между векторами 21
AA
и
41
AA
, пользуясь определением скалярного произведения: [13].
)cos(
412141214121
AAAAAAAAAAAA
∧
⋅⋅=⋅
,
4121
4121
4121
)cos(
AAAA
AAAA
AAAA
⋅
⋅
=
∧
)1;1;1(
21
−AA
;
)2;2;0(
41
−−AA
;
8
41
=AA
.
0
62
0
83
)2()1()2(101
)cos(
4121
==
⋅
−⋅−+−⋅+⋅
=
∧
AAAA
2
)(
4121
π
=
∧
AAAA
2)
Площадь грани
321
AAA
вычислим с помощью векторного произведения
[1].
3121
2
1
321
AAAAS
AAA
×=
∆
,
)1;1;1(
21
−AA
,
)2;1;1(
31
−AA
kjikji
kji
AAAA 23
11
11
21
11
21
11
211
111
3121
+−=
−
+
−
−
−
−
−
=
−
−=×
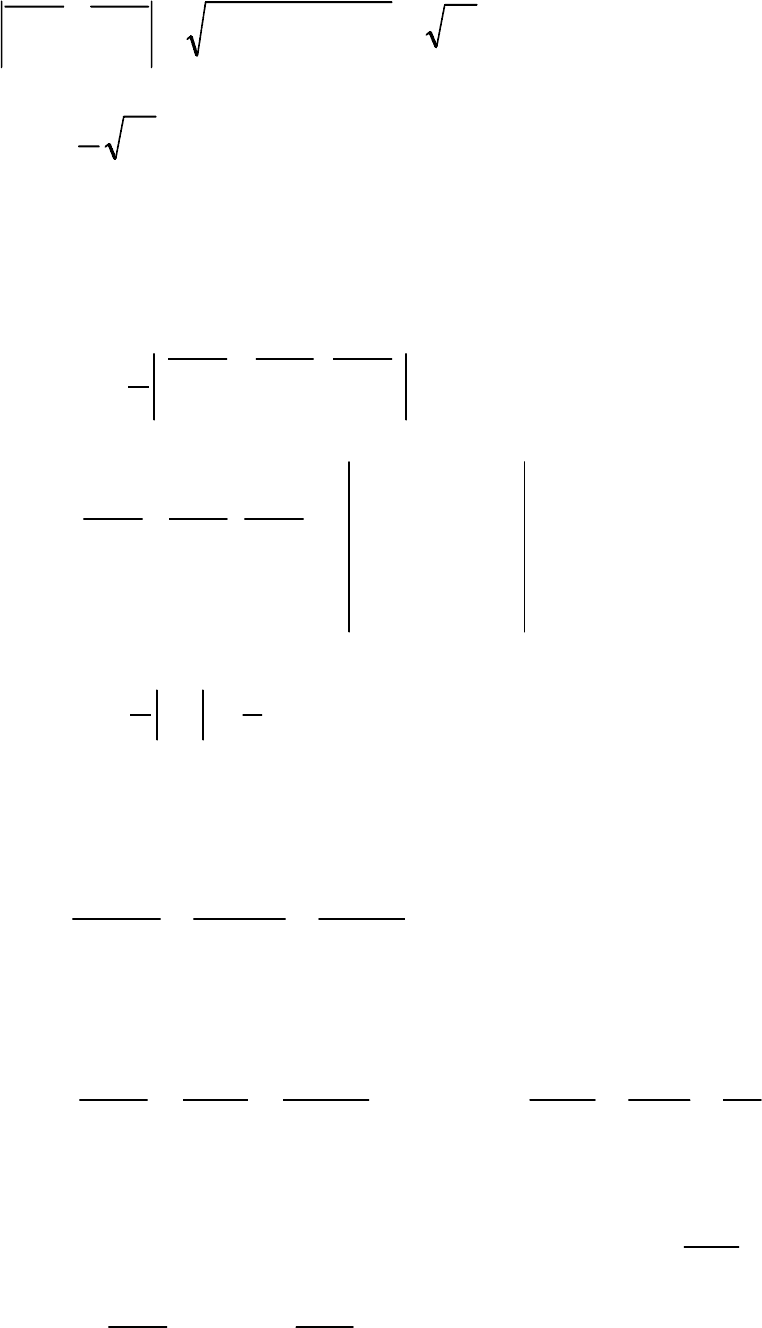
16
142)1(3
222
3121
=+−+=× AAAA
).(87.114
2
1
2
едS ≈=
∆
3)
Объем пирамиды
321
AAA
вычислим с помощью смешанного
произведения трех векторов, на которых построена пирамида, [9].
)(
6
1
413121
AAAAAAV ⋅×=
2
220
211
111
)(
413121
−=
−−
−
−
=⋅× AAAAAA
)(
3
1
2
6
1
3
едV =−=
4)
Уравнение прямой 21
AA
найдем по формуле:
,
12
1
12
1
12
1
zz
zz
yy
yy
xx
xx
−
−
=
−
−
=
−
−
уравнение прямой, проходящей через две точки [1]
01
0
12
1
23
2
−−
−
=
−
−
=
−
− zyx
11
1
1
2
−
=
−
=
−
zyx
.
5)
Для того, чтобы составить уравнение плоскости
321
AAA
, возьмем
текущую точку
);;( zyxM
плоскости. Векторы
);1;2(
1
zyxMA −−
,
)1;1;1(
21
−AA
,
)2;1;1(
31
−AA
лежат в этой плоскости, т.е. они являются
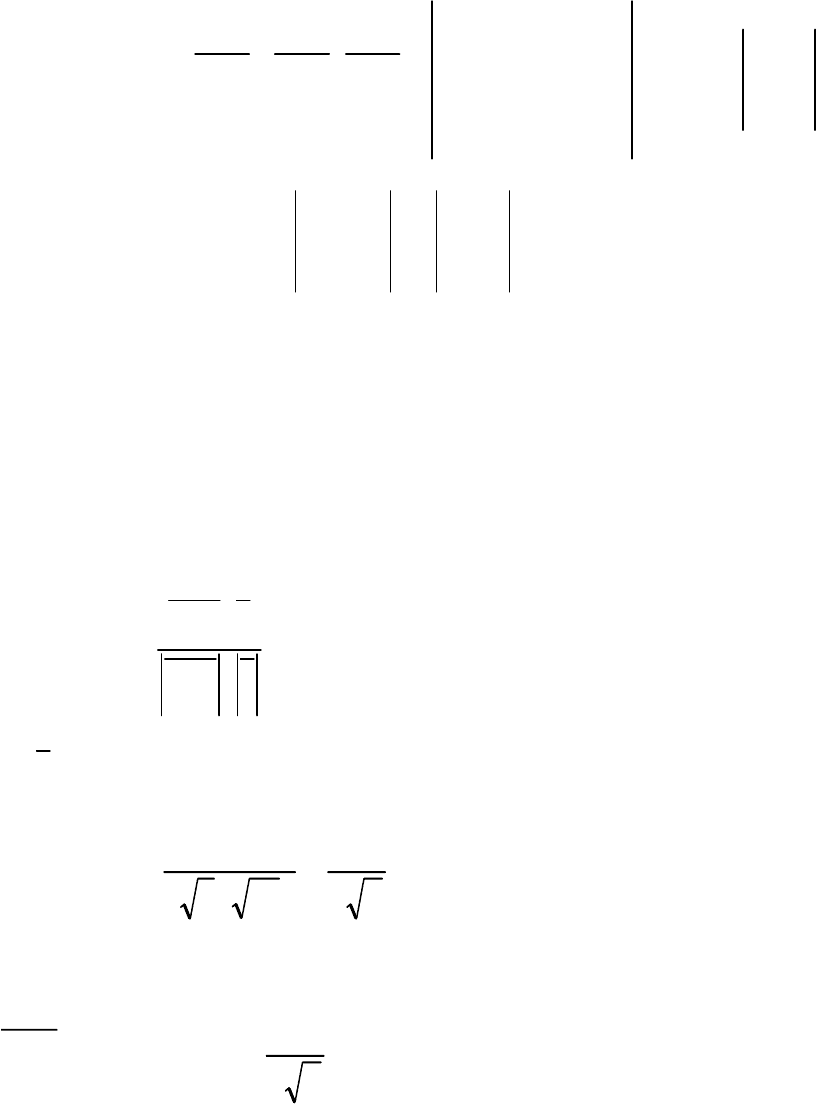
17
компланарными. Воспользуемся условием компланарности трех
векторов:
−
−
−=
−
−
−−
=⋅×
21
11
)2(
211
111
12
31211
x
zyx
AAAAMA
=+−−−=
−
+
−
−
− zyxzy 2)1()2(3
11
11
21
11
)1(
523
+
+
−
=
zyx
В силу условия компланарности уравнение плоскости
321
AAA
имеет вид:
0523
=
−
+
−
zyx
7) Угол между ребром
41
AA
и гранью
321
AAA
(
α
) найдем по формуле
nAA
nAA
AA
⋅
⋅
=
∧
41
41
41
)sin(
α
где
)2;1;3( −n
нормальный вектор плоскости
321
AAA
.
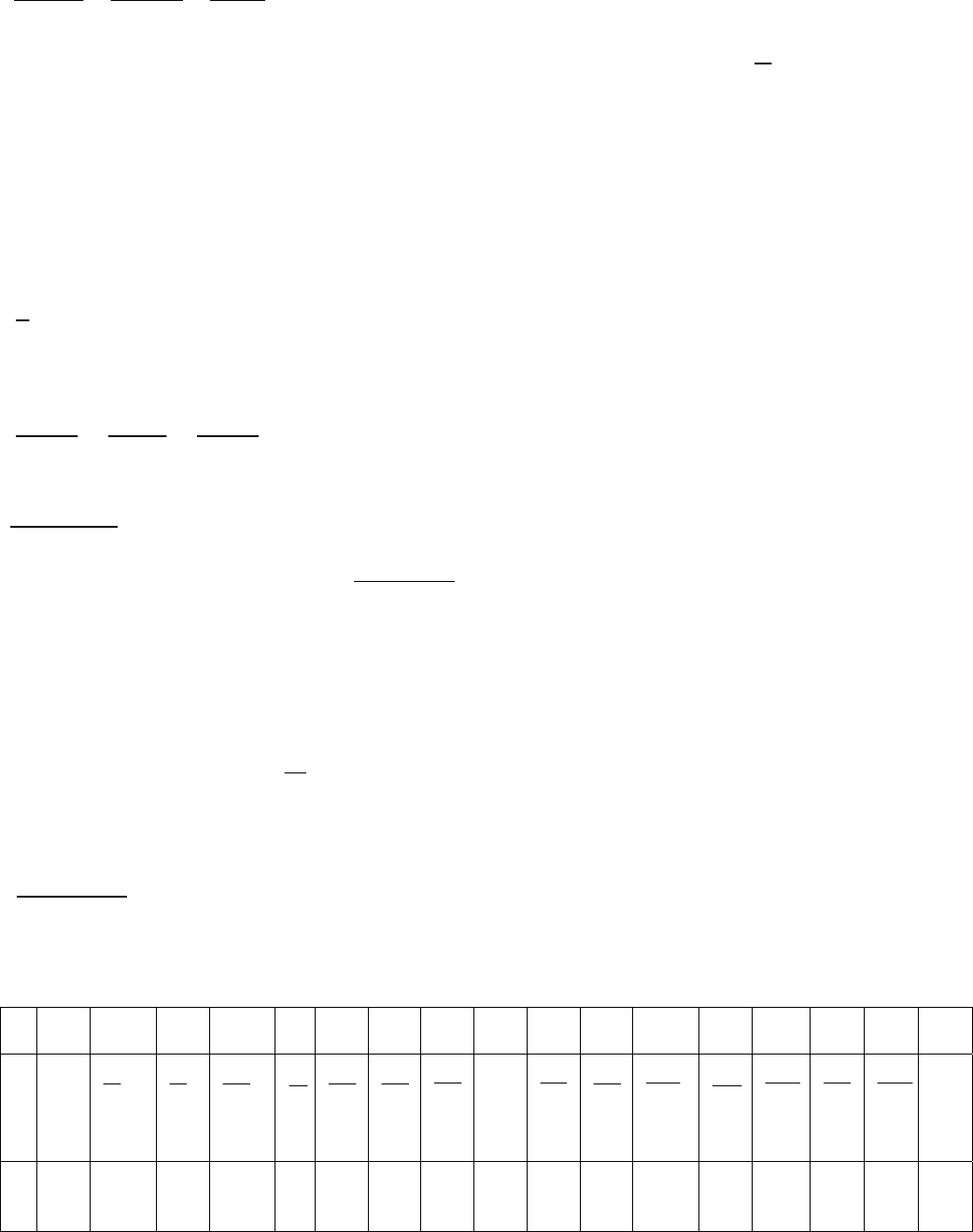
72
1
148
4230
)sin(
41
−
=
⋅
−+⋅
=
∧
α
AA
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
∧
72
1
arcsin)(
41
α
AA
.
8) Чтобы составить уравнение высоты, опущенной из вершины
4
A
на грань
321
AAA
, воспользуемся каноническими уравнениями прямой
18
p
zz
e
yy
m
xx
−
=
−
=
−
00
, где 000
,, zyx
- координаты точки, через которую
проходит прямая, а
p
em ,,
- координаты направляющего вектора
S
[10].
Искомая прямая проходит через точку
)2;1;2(
4
−
−
A
. Так как прямая и плоскость
321
AAA
перпендикулярны, то нормальный вектор плоскости
0523
=
−
+− zyx
параллелен прямой. Поэтому за направляющий вектор прямой берем вектор
)2;1;3( −n
. Уравнение прямой, опущенной из вершины
4
A
, имеют вид :
2
2
1
1
3
2 +
=
−
+
=
− zyx
.
Задача 3.
Линия задана уравнением
ϕ
sin2
3
+
=r
в полярной системе координат.
Требуется:
1)
построить линию по точкам, начиная от
0
=
ϕ
до
π
ϕ
2
=
, придавая значения
ϕ
через промежуток
0
5,22
8
=
π
;
2)
найти уравнение данной линии в декартовой системе координат.
Решение.
Для построения линии в полярной системе координат составим таблицу значений
полярного радиуса
r
при определенных значениях полярного угла
ϕ
[1]
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
ϕ
0
8
π
4
π
8
3
π
2
π
8
5
π
4
3
π
8
7
π
π
8
9
π
4
5
π
8
11
π
2
3
π
8
13
π
4
7
π
8
15
π
π
2
r
1,5 1,27 1,1 1,03 1 1,03 1,1 1,27 1,5 1,85 2,33 2,7 3 2,7 2,33 1,85 1,5
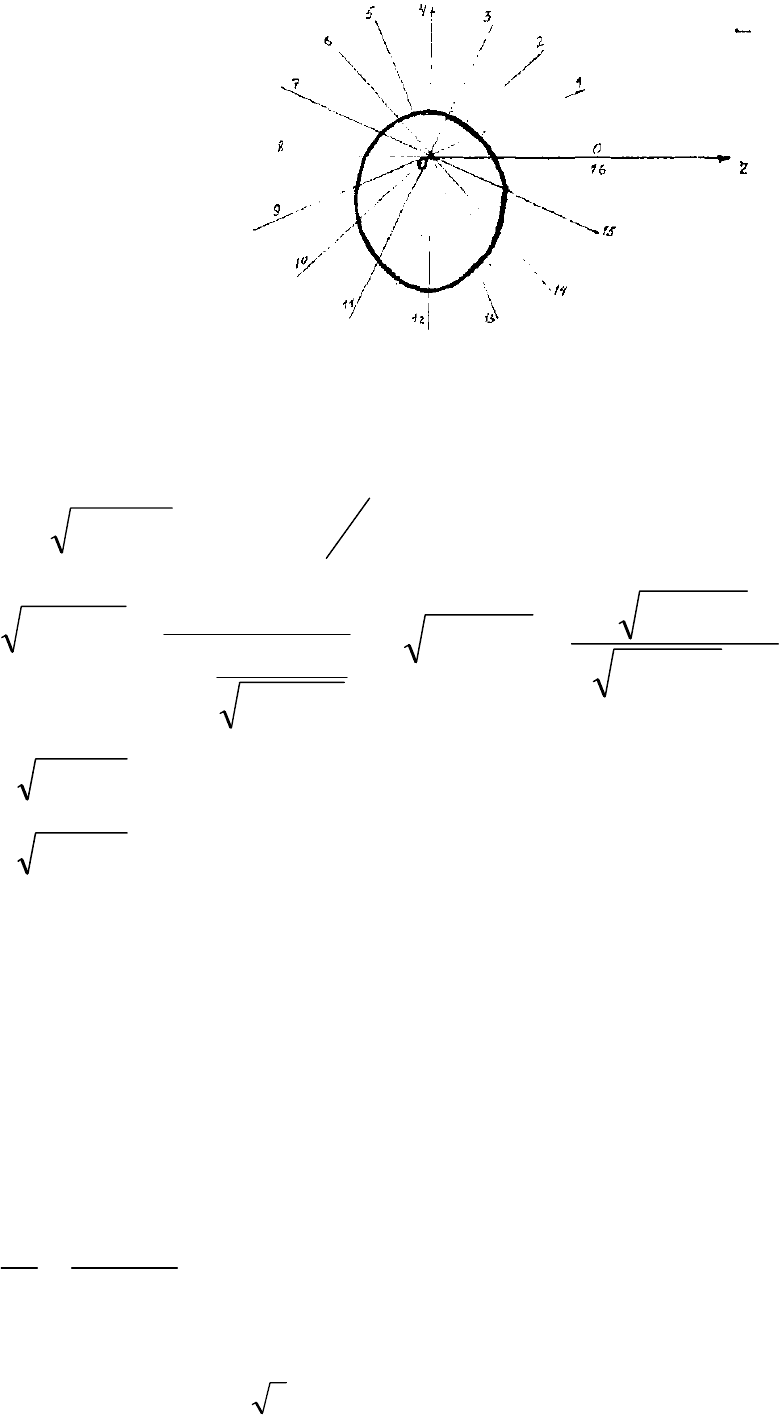
19
Для получения уравнения в декартовой системе координат используем формулы
перехода от полярной системы координат к декартовой:
,
22
yxr +=
.sin
r
y
=
ϕ
;
2
3
22
22
yx
y
yx
+
+
=+
;
2
3
22
22
22
yyx
yx
yx
++
+
=+
;32
22
=++ yyx
;32
22
yyx −=+
;69)(4
222
yyyx +−=+
;09634
22
=−++ yyx
[]
;04)1(34
22
=−++ yx
;012)1(34
22
=−++ yx
;12)1(34
22
=++ yx
.1
4
)1(
3
22
=
+
+
yx
Получили уравнение эллипса с центром в точке (0;-1); большой полуосью
b = 2,
малой полуосью
3=a
[1].

20
Задача 4.
Дана система линейных уравнений
⎪
⎩
⎪
⎨
⎧
=+−−
−=+−
=++
.422
,123
,22
321
321
321
xxx
xxx
xxx
Доказать ее совместность и решить двумя способами:
а) методом Гаусса;
б) матричным методом.
Решение.
Для совместности системы необходимо и достаточно, чтобы ранг матрицы
системы равнялся рангу расширенной матрицы этой системы (теорема Кронекера
– Капелли) [1]. Матрица А системы состоит из коэффициентов при неизвестных
.
212
213
112
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
−=A
Если к матрице системы добавить столбец из свободных членов, то получим
расширенную матрицу системы
.
422
123
212
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−=B
Под рангом понимается наибольший порядок минора, отличного от нуля. Для
матрицы А минором наивысшего порядка, равного трем, является ее
определитель [3]:
.015
212
213
112
det ≠−=
−−
−=A
Следовательно,
3
=
rgA
.
