Циценкова Г.А., Чукавина Т.В., Рязанова Л.Д., Труппова В.А. Методические указания и контрольные задания по высшей математике
Подождите немного. Документ загружается.


21
В матрице В нет минора порядка больше 3, а
Adet
является одним из ее миноров
третьего порядка, поэтому
3
=
rgB
.
Система совместна, так как
3
=
=
rgBrgA
.
а) Решение методом Гаусса состоит в преобразовании системы к треугольному
виду, что достигается исключением неизвестных х
1
из 2-го и 3-го уравнений и х
2
–
из 3-го уравнения. Последовательное исключение неизвестных осуществляется с
помощью элементарных преобразований системы, приводящих к равносильной
системе, к которым относятся [1]:
1)
перестановка любых двух уравнений;
2)
умножение обеих частей одного уравнения на любое отличное от нуля число;
3)
прибавление к обеим частям одного уравнения соответствующих частей
другого, умноженных на любое число.
Все преобразования, связанные с последовательным исключением
неизвестных, удобнее применять не к самой системе линейных уравнений, а к ее
расширенной матрице. Получающиеся при этом матрицы называются
эквивалентными и соединяются знаком
.
6
8
3
3
1
1
0
5
2
0
0
1
~
4
2
3
2
1
1
1
1
2
2
2
1
~
4
3
2
2
1
1
1
2
1
2
1
2
~
4
1
2
2
2
1
1
1
1
2
3
2
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
−
−
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
−
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
−
−
(вертикальной чертой отделены элементы матрицы А).
Были проведены следующие действия:
1)
из элементов второй строчки вычли элементы первой строки;
2)
первую и вторую строки поменяли местами;
3)
к элементам второй строки прибавили соответствующие элементы первой
строки, умноженные на (-2);
4)
к элементам третьей строки прибавили соответствующие элемент второй
строки.
Полученной матрице соответствует система уравнений:

22
⎪
⎩
⎪
⎨
⎧
=
=−
−=+−
.63
,85
,32
3
32
321
x
xx
xxx
Решая уравнения снизу вверх, имеем
,2)28(
5
1
)8(
5
1
,2
323
=+=+== xxx
.124323
321
−
=
−+−
=
−+−= xxx
Ответ: (-1, 2, 2).
б) Для решения системы матричным методом вводим матрицы
,
2
2
1
1
1
1
2
3
2
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
−
=A
,
3
2
1
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
x
x
x
X
.
4
1
2
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−=C
Тогда эта система запишется в виде матричного уравнения
АХ=С [13].
Умножив левую и правую части уравнения на
А
-1
слева, получим
А
-1
АХ=А
-1
С,
где
А
-1
– обратная матрица.
Так как
А
-1
А=Е, то Х=А
-1
С.
,
det
1
33
32
31
23
22
21
13
12
11
1
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
−
A
A
A
A
A
A
A
A
A
A
A
где
;)1(
ij
ji
ij
MA
+
−=
ij
A
- алгебраическое дополнение, соответствующее элементу
ij
a
;
ij
M
- минор (определитель), который получается из матрицы А после
вычеркивания i-ой строки и j-го столбца.
Найдем алгебраические дополнения:
;3
21
11
;3
21
11
;0
21
21
312111
=
−
=−=
−
−==
−
−
= AAA

23
;1
23
12
;6
22
12
;10
22
23
322212
−=−==
−
=−=
−
−= AAA
.5
13
12
;0
12
12
;5
12
13
332313
−=
−
==
−−
−=−=
−−
−
= AAA
Cледовательно:
.
5
1
3
0
6
3
5
10
0
15
1
1
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
−
−
−
−
=
−
A
Пользуясь правилом умножения матриц получим решение системы [10]:
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
−
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⋅−+−⋅+⋅−
⋅−+−⋅+⋅−
⋅+−⋅−+⋅
−
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
−
−
−
−
=
30
30
15
15
1
4)5()1(025
4)1()1(6210
43)1()
3(20
15
1
4
1
2
5
1
3
0
6
3
5
10
0
15
1
X
,
2
2
1
)30(
30
)30(
30
)15(
15
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
=
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
−
−
−
−
=
.
2
2
1
3
2
1
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
x
x
x
X
откуда
.2;2;1
321
=
=
−= xxx
Сравните ответы, полученные при решении системы методом Гаусса и
матричным методом.
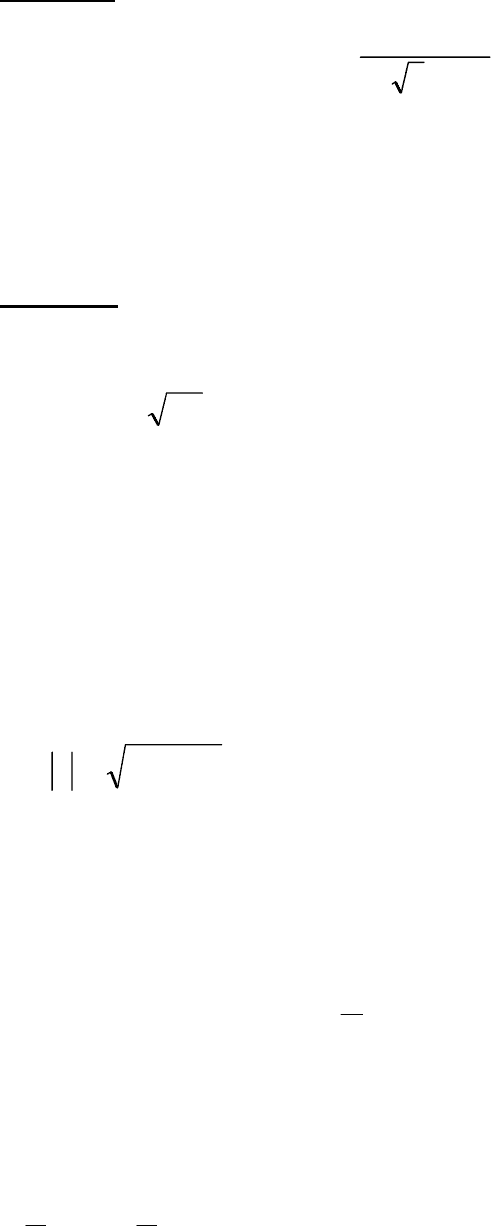
24
Задача 5.
Дано комплексное число
i
ii
Z
+
−
+
=
3
)1)(1(
.
Требуется: 1) записать число Z в алгебраической и тригонометрической формах;
2) найти все корни уравнения
.0
3
=+ Zw
Решение.
1) Комплексными называются числа вида z=x+iy, где x и y – действительные
числа, а
1−=i
- мнимая единица. Числа x и y называются соответственно
действительной и мнимой частями комплексного числа
Z. Число z=x-iy
называется сопряженным числу z=x+iy. С геометрической точки зрения числу Z
можно сопоставить вектор, направленный из начала координат в точку
Z с
координатами
x и y [7]. Длина этого вектора называется модулем комплексного
числа и определяется равенством
22
yxzr +==
.
Угол, образованный вектором
Z с положительным направлением оси ОХ,
называется аргументом числа
Z и обозначается Arg z. Для аргумента ϕ
справедливы формулы [7]:
ϕϕϕ
tg
x
y
ryrx === ,sin,cos
значения
Arg z определяются не однозначно, а с точностью до слагаемого 2k
π
(k=0; ±1; ±2; …)
. Arg z=аrg z+2k
π
, где аrg z – главное значение аргумента,
2
arg
2
π
π
≤<−
.
Тригонометрическая форма комплексного числа
z=x+iy имеет вид [7]
),sin(cos
ϕ
ϕ
irz +=
где

25
r
- модуль комплексного числа,
ϕ
- главное значение его аргумента.
Данное число
)3()1)(1( iiiz +−+=
запишем в алгебраической форме. Для
этого в числителе раскроем скобки и умножим числитель и знаменатель на число
сопряженное знаменателю. Получим:
.
22
3
13
)3(2
)3)(3(
)3)(1(
2
ii
ii
ii
Z −=
+
−
=
−+
−−
=
Чтобы число
22
3 i
Z −=
записать в тригонометрической форме, найдем его
модуль и главное значение аргумента:
;1
4
1
4
3
22
=+=+= yxr
.
6
3
1
π
ϕ
−=
⎟
⎠
⎞
⎜
⎝
⎛
−== arctg
x
y
arctg
(
)
(
)
.
6
sin
6
cos
6
sin
6
cos)sin(cos
π
π
π
π
ϕϕ
iiirz −=−+−=+=
2) Решим уравнение
.0
22
3
3
=−+
i
w
;
22
3
3
i
w +−=
.
22
3
3
i
w +−=
Чтобы найти все корни n-ой степени из числа Z, воспользуемся формулой [9]:
,
2
sin
2
cos
⎟
⎠
⎞
⎜
⎝
⎛
+
+
+
=
n
k
i
n
k
rZ
nn
πϕπϕ
).1(,...,2,1,0 −
=
nk
Для числа
22
3
i
z +−=
найдем модуль и аргумент.
,1
4
1
4
3
=+== zr
т.к.
,
2
3
cos −==
r
x
ϕ
,
2
1
sin ==
r
y
ϕ
то
.
6
5
π
ϕ
=

26
Итак:
,
3
2
6
5
sin
3
2
6
5
cos
22
3
3
π
π
π
π
k
i
k
i
w
+
+
+
=+−=
.2,1,0=k
;
18
5
sin
18
5
cos
36
5
sin
36
5
cos
0
π
π
π
π
iiw +=
⋅
+
⋅
=
;
18
17
sin
18
17
cos
3
2
6
5
sin
3
2
6
5
cos
1
ππ
π
π
π
π
iiw +=
+
+
+
=
.
18
29
sin
18
29
cos
3
4
6
5
sin
3
4
6
5
cos
2
ππ
π
π
π
π
iiw +=
+
+
+
=
27
Раздел 2. Введение в математический анализ,
производная и ее приложения.
Вопросы для самоподготовки.
1. Понятие переменной и постоянной величины. Параметры и абсолютные
константы.
2.
Определение функции, область определения, область значений функций,
основные способы задания. Определение четной, нечетной,
периодической функции, сложной функции.
3.
Графики и свойства элементарных функций.
4.
Определение предела функции при стремлении аргумента к некоторому
конечному пределу и предела функции при стремлении аргумента к
бесконечности, односторонние пределы. Основные теоремы о пределах.
5.
Бесконечно малые и бесконечно большие функции, связь между ними,
свойства бесконечно малых функций. Сравнение бесконечно малых.
Эквивалентные бесконечно малые.
6.
Первый и второй классические пределы.
7.
Определения непрерывности функции в точке и на отрезке. Свойства
непрерывных функций.
8.
Классификация точек разрыва функции.
9.
Свойства функции, непрерывной на замкнутом отрезке.
10.
Понятие приращения аргумента и функции. Определение производной, ее
механический и геометрический смысл.
11.
Основы правила дифференцирования функций.
12.
Производная сложной функции.
13.
Вывод формул производной степенной, тригонометрических,
логарифмической, показательной функций.
14.
Производная обратной функций.
15.
Вывод формул производных обратных тригонометрических функций.
16.
Логарифмическое дифференцирование.

28
17. Производная параметрически заданной функции, неявно заданной
функции.
18.
Дифференциал функции. Инвариантность формы первого дифференциала.
Формула дифференциала функции. Применение дифференциала к
приближенным вычислениям значений функции в заданной точке.
19.
Производные и дифференциалы высших порядков. Механический смысл
второй производной.
20.
Основные теоремы дифференциального исчисления: Ролля, Лагранжа,
Коши.
21.
Правило Лопиталя. Типы неопределенности, для раскрытия которых
может быть использовано правило Лопиталя.
22.
Формула Тейлора. Разложение функций по формулам Тейлора функций.
23.
Возрастающие и убывающие функции. Условия монотонности функций.
24.
Экстремум функции. Необходимое и достаточное условия существования
экстремума.
25.
Наибольшее и наименьшее значение функции на отрезке.
26.
Выпуклость, вогнутость, точки перегиба графика функции, условия их
существования.
27.
Асимптоты графика функции.
Контрольные задания
Задача 6.
Найти пределы функций, не пользуясь правилом Лопиталя.
6.1.
а)
23
21
lim
−
−
∞→
x
x
x
;
б)
x
xx
x
3
11
lim
0
−−+
→
;
в)
2
0
5
cos1
lim
x
x
x
−
→
;
г)
x
x
x
x
⎟
⎠
⎞
⎜
⎝
⎛
−
+
∞→
2
3
lim
;

29
6.2.
а)
12
1
3
3
lim
+
+
∞→
x
x
x
;
б)
7
32
lim
7
−
−+
→
x
x
x
;
в)
x
x
x
5
3arcsin
lim
0→
;
г)
x
x
x
x
⎟
⎠
⎞
⎜
⎝
⎛
+
−
∞→
12
12
lim
;
6.3.
а)
2
52
3
23
lim
−+
−+
∞→
xx
xx
x
;
б)
xx
xx
x
−
−
→
2
1
lim
;
в)
x
x
x
2cos1
lim
0
−
→
;
г)
x
x
x
x
x
2
4
14
lim
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
∞→
;
6.4.
а)
22
63
4
24
lim
+−
−+
∞→
xx
xx
x
;
б)
131
lim
0
−+
→
x
x
x
;
в)
arctgx
x
x
5
lim
0→
;
г)
x
x
x
1
)21(
lim
+
∞→
;
6.5.
а)
15
562
2
2
lim
−−
−+
∞→
xx
xx
x
;
б)
2
2
0
11
lim
x
x
x
−−
→
;
в)
2
3
0
coscos
lim
x
xx
x
−
→
;
г)
[
]
xxx
x
ln)1ln(
lim
−+⋅
+∞→
;
6.6.
а)
112
53
4
4
lim
+−
++
∞→
xx
xx
x
;
б)
2
0
2131
lim
xx
xx
x
+
−−+
→
;
в)
;
3sin
2
2
0
lim
x
xctgx
x→
г)
[
]
xxx
x
ln)3ln()12(
lim
−++
∞→
;
6.7.
а)
42
42
32
52
lim
xx
xxx
x
++
+−
∞→
;
б)
32
2
0
131
lim
xx
x
x
+
−+
→
;
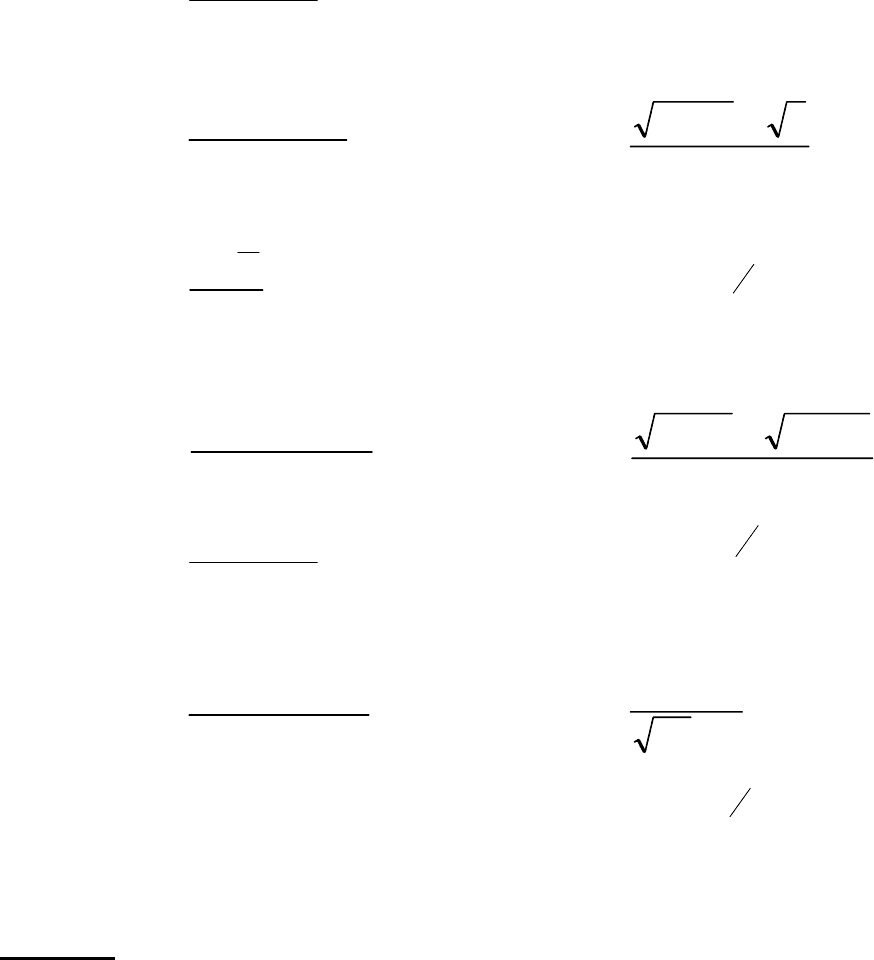
30
в)
x
x
x
2cos1
6cos1
lim
0
−
−
→
;
г)
[
]
xxx
x
ln)3ln()5(
lim
−−−
∞→
6.8.
а)
53
135
2
2
lim
−+
+−
∞→
xx
xx
x
;
б)
3
512
lim
3
−
−−
→
x
x
x
;
в)
2
2
0
2
lim
x
x
tg
x→
;
г)
)33(
1
)67(
lim
−
→
−
x
x
x
x
6.9.
а)
3
227
4
34
lim
+
+−
∞→
x
xx
x
;
б)
xx
xx
x
5
6231
2
5
lim
−
+−+
→
;
в)
xtgx
x
x
22
4cos1
lim
0
⋅
−
→
;
г)
)4(
2
2
2
)53(
lim
−
→
−
x
x
x
x
;
6.10.
а)
522
938
25
25
lim
++
+−
∞→
xx
xx
x
;
б)
22
2
lim
2
−
−
→
x
x
x
;
в)
xctgx
x
35
lim
0
⋅
→
;
г)
)3(
2
3
)83(
lim
−
→
−
x
x
x
;
Задача 7.
Задана функция
)(xfy =
. Найти точки разрыва функции, если они
существуют. Сделать чертеж.
7.1.
⎪
⎩
⎪
⎨
⎧
≥
<≤−+
−<+
=
.1,2
;11,2
;1,4
)(
2
xx
xx
xx
xf
