Циценкова Г.А., Чукавина Т.В., Рязанова Л.Д., Труппова В.А. Методические указания и контрольные задания по высшей математике
Подождите немного. Документ загружается.

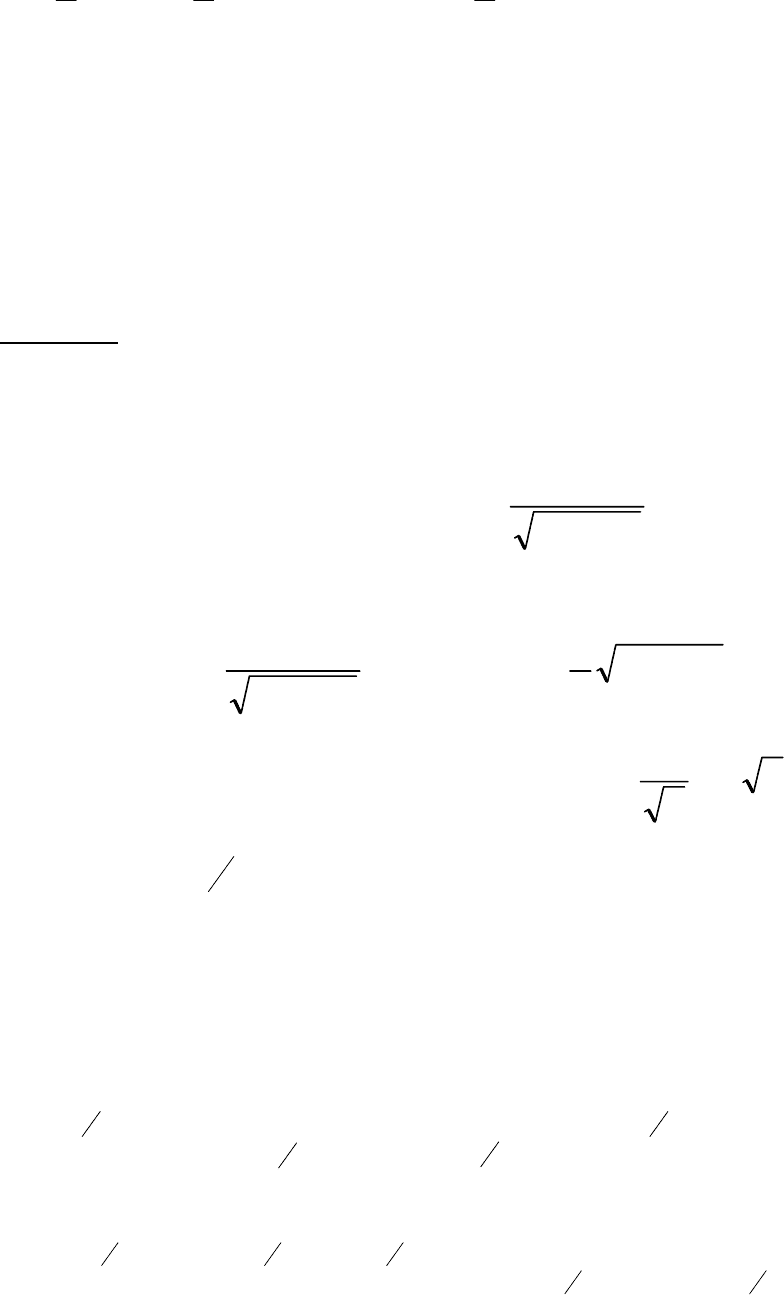
71
.5sin)7(5cos
5
1
)5sin5)(7(
5
1
5cos
5
1
xxxxxx −=+−−−−=
(для проверки была использована формула
()
vuvuuv
′
+
′
=
′
.
6.3.
(б)
∫
xdx4arccos
Решение.
Интеграл от обратных тригонометрических функций берется по частям.
∫
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
=
−
−
=
=
=
=
xv
x
dx
du
dxdv
xu
xdx
2
161
4
,
,4arccos
4arccos
,161
4
1
4arccos
161
4
4arccos
2
2
cxxx
x
xdx
xx +−−=
−
+=
∫
(последний интеграл берется с помощью формулы
cu
u
du
+=
∫
2
).
6.4.
(в)
dxex
x
∫
−
2
2
Интеграл вида
dxexP
x
n
∫
α
)(
берется по частям, так как подынтегральная
функция представляет произведение алгебраической функции на трансцедентную.
+−=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
−=
=
=
=
=
−
−
−
−
∫
2
2
2
2
2
2
2
2
2
2
,
,
x
x
x
x
ex
ev
xdxdu
dxedv
xu
dxex
∫∫
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
−=
=
=
=
=+−=+
−−
−−−
22
22
2
2
2,
,
424
xx
xxx
ev
dxdu
dxedv
xu
dxxeexdxxe
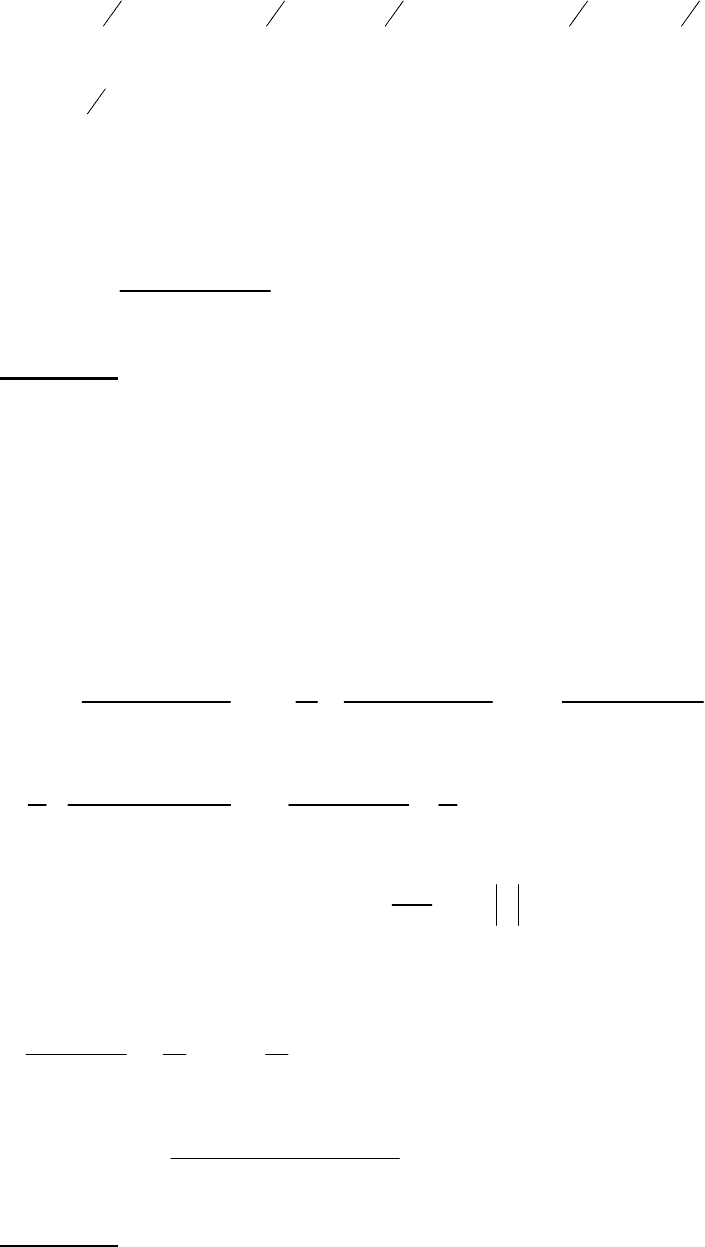
72
(
)
−−−=+−+−
−−−−−
∫
22
2
222
2
822242
xxxxx
xeexdxexeex
.16
2
ce
x
+−
−
В данном примере формула интегрирования по частям была использована
дважды.
6.3. (а)
dx
xx
x
∫
+−
−
22
3
2
Решение.
Данный интеграл является интегралом от простейшей рациональной дроби
третьего типа (квадратный трехчлен
(
)
22
2
+− xx
имеет отрицательный
дискриминант) [7]. При интегрировании в числителе запишем производную от
квадратного трехчлена и выравниваем коэффициенты по условию. После
почленного деления и выделения полного квадрата в знаменателе получаем
=
+−
−
+−
−
=
+−
−
=
∫∫∫
1)1(
2
22
)22(
2
1
22
3
222
x
dx
xx
dxx
dx
xx
x
J
.)1(2)22ln(
2
1
1)1(
)1(
2
22
)22(
2
1
2
22
2
cxarctgxx
x
xdx
xx
xxd
+−−+−=
+−
−
−
+−
+−
=
∫∫
(Первый
интеграл берется по формуле:
,ln cu
u
du
+=
∫
где
22
2
+−= xxu
. Второй
интеграл берется по формуле:
,
1
22
c
a
u
arctg
aua
du
+=
+
∫
где
1,1
=
−
=
axu
).
6.3. (б)
∫
+−
++−
= dx
xxx
xxx
J
22
232
23
23
Решение.
Подынтегральная функция представляет собой неправильную рациональную
дробь.
Выделим целую часть [4]:

73
.
22
2
1
22
232
2323
23
xxx
x
xxx
xxx
+−
+
+=
+−
++−
Полученную правильную рациональную дробь разложим на простейшие дроби,
предварительно разложив знаменатель на простые множители:
.
22)22(
2
22
2
2223
+−
+
+=
+−
+
=
+−
+
xx
CBx
x
A
xxx
x
xxx
x
Справа приводим дроби к общему знаменателю и записываем равенство
числителей:
).()22(2
2
CBxxxxAx +++−=+
Коэффициенты А, В, С, находим методом частных значений, подставляя в
полученное равенство вместо Х вещественные корни знаменателя:
.1,22,0 === AAx
Для определения остальных коэффициентов берем дополнительные значения Х:
.3
,1
4
2
,51
,3
,1
,1
=
−=
⇒
⎩
⎨
⎧
−=−
=+
−+=
++=
−=
=
C
B
CB
CB
CBA
CBA
x
x
Найденные значения А, В, С подставляем в разложение дроби и получаем
интеграл
∫
⎟
⎠
⎞
⎜
⎝
⎛
+−
+−
++= dx
xx
x
x
J
22
31
1
2
(см. предыдущий пример)
(
)
.)1(2)22ln(
2
1
ln
2
cxarctgxxxxJ +−++−−+=
6.3. (в)
∫
+−
+
=
)44(
)4(
23
xxx
dxx
J
Интегрируем правильную рациональную дробь, разлагая ее на простейшие дроби:
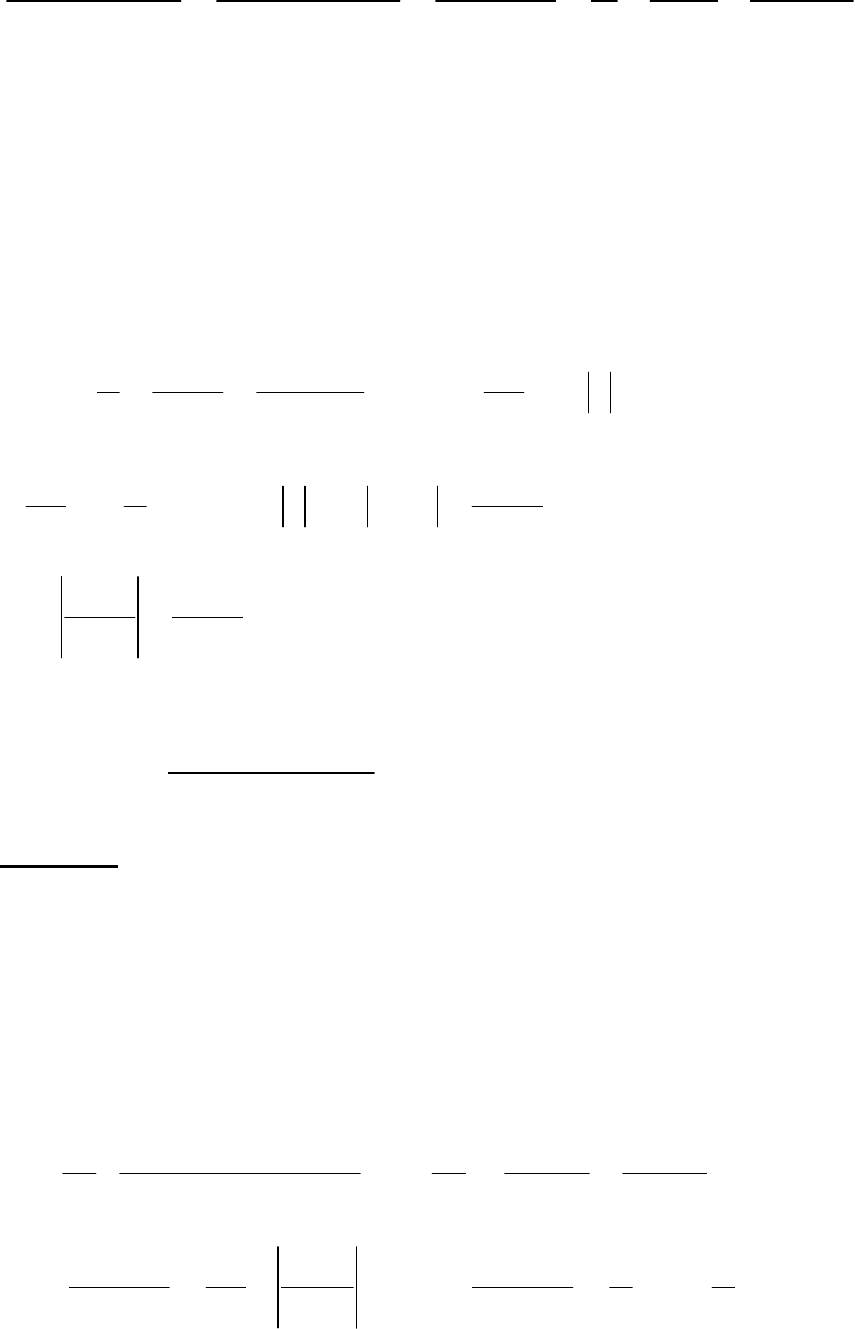
74
.
)2(2)2(
4
)44(
4
44
4
22223
−
+
−
+=
−
+
=
+−
+
=
+−
+
x
C
x
B
x
A
xx
x
xxx
x
xxx
x
Справа
приводим дроби к общему знаменателю и записываем равенство числителей:
CxxBxxAx +−+−=+ )2()2(4
2
.1
;3
;1
,337
,26
,44
,3
,2
,0
−=
=
=
++=
=
=
=
=
=
B
C
A
CBA
C
A
x
x
x
∫∫
⎩
⎨
⎧
+==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
−
−= ;ln
)2(
3
2
11
2
Cu
u
du
dx
xxx
J
∫
=+
−
−−−=
⎭
⎬
⎫
+−= C
x
xxC
uu
du
2
3
2lnln
1
2
.
2
3
2
ln C
xx
x
+
−
−
−
=
6.3. (г)
∫
+−
= .
)9)(4(
22
xx
dx
J
Решение.
Для интегрирования данной правильной рациональной дроби нужно разложить ее
на простейшие дроби, а затем, как в предыдущем примере, найти коэффициенты и
проинтегрировать каждую из простейших дробей. Однако этот интеграл можно
взять иначе, учитывая, что в знаменателе стоят скобки, и выполняя
преобразование числителя:
∫∫
=
⎟
⎠
⎞
⎜
⎝
⎛
+
−
−
=
+−
−−+
= dx
xx
dx
xx
xx
J
9
1
4
1
13
1
)9)(4(
)4()9(
13
1
2222
22
=
⎭
⎬
⎫
⎩
⎨
⎧
+=
+
+
+
−
=
−
=
∫∫
C
a
u
arctg
aau
du
C
au
au
aau
du 1
;ln
2
1
2222
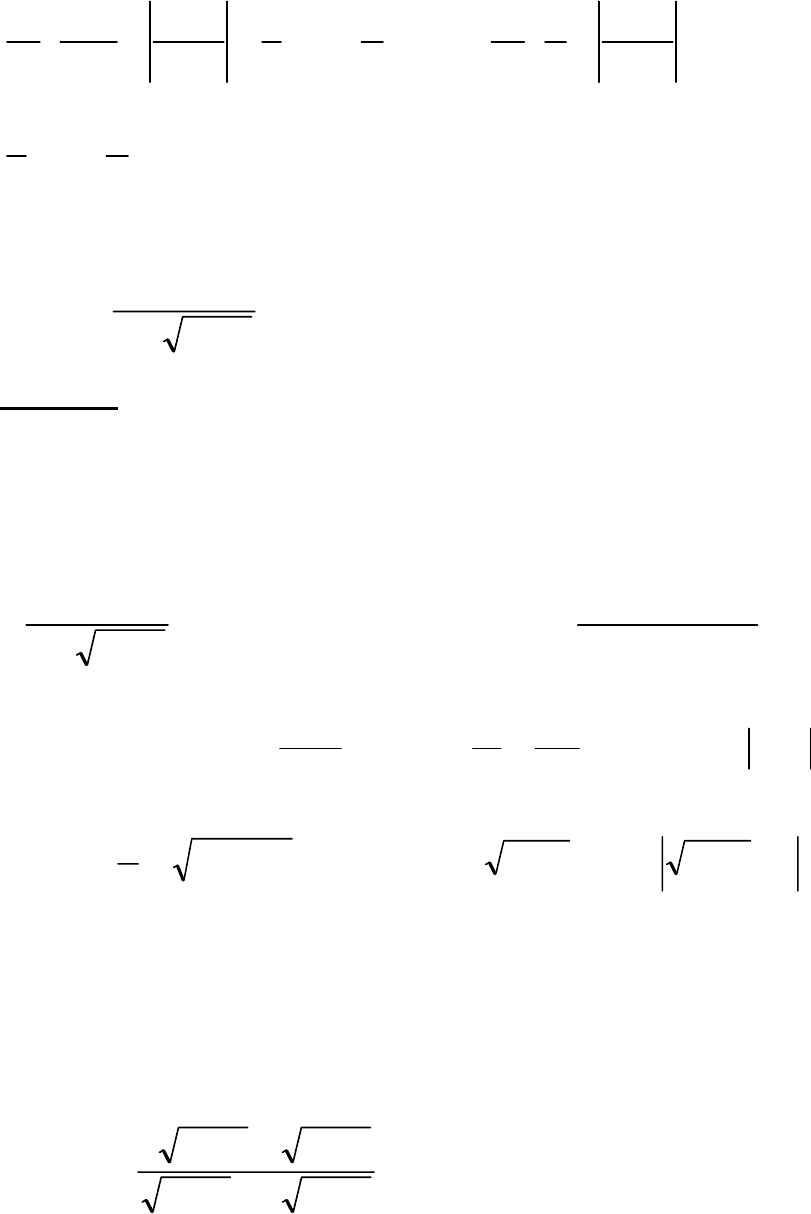
75
⎜
⎜
⎝
⎛
−
+
−
=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
−
⋅ 2
2
ln
4
1
13
1
33
1
2
2
ln
22
1
13
1
x
x
C
x
arctg
x
x
.
33
1
C
x
arctg +
⎟
⎠
⎞
6.4. (а)
∫
−−
+
23
)1(
x
dxx
Решение.
Подынтегральная функция содержит иррациональное выражение. Для
интегрирования таких выражений делается замена, устраняющая
иррациональность.
∫∫
=
−
+−
=
⎭
⎬
⎫
⎩
⎨
⎧
=
+=
=−
=
−−
+
3
)3(2
2
,2
,2
23
)1(
2
2
2
t
dttt
tdtdx
tx
tx
x
dxx
∫
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
−+++−=
⎟
⎠
⎞
⎜
⎝
⎛
−
+++−= 3ln3612
2
3
3
2
3
36
1232
23
2
tt
tt
dt
t
tt
.32ln72224)2(3)2(
3
2
3
cxxxxc +−−−−−−−−⋅
⎟
⎠
⎞
⎜
⎝
⎛
−=+
Замечание.
После замены переменной под знаком интеграла дробь стала неправильной,
поэтому сначала пришлось выделить целую часть, а затем проинтегрировать
полученное выражение.
6.5.
(б)
.
222
224
3
6
dx
xx
xx
∫
−+−
−−−
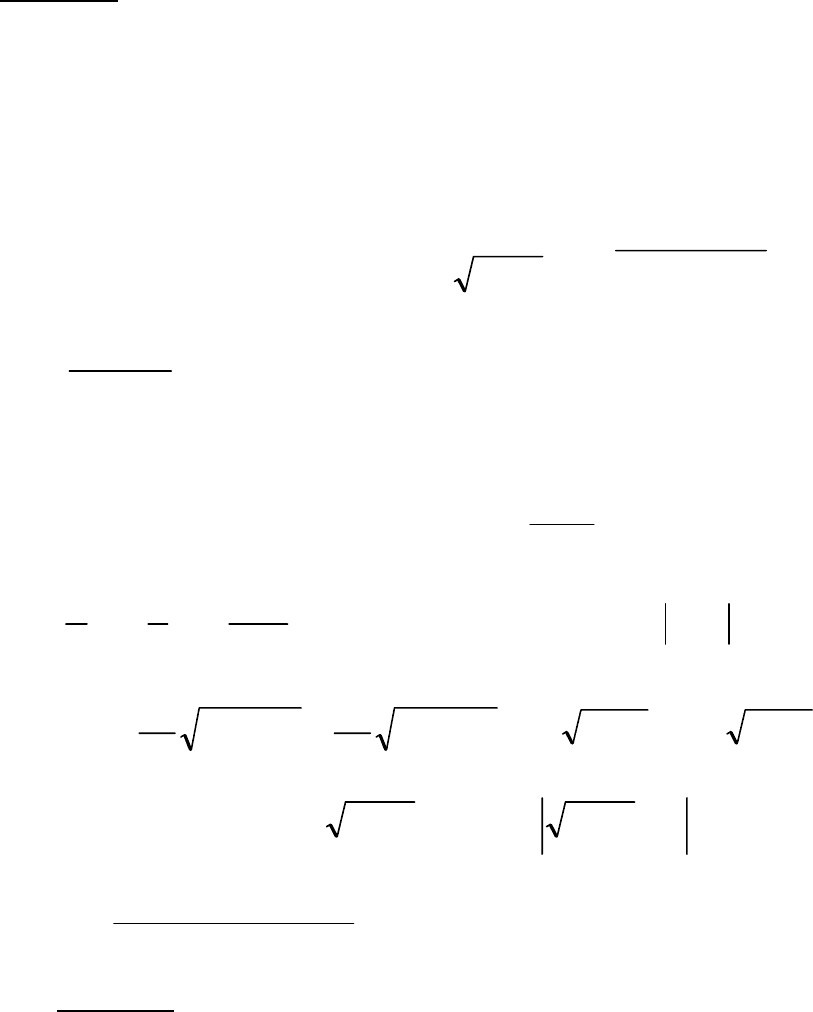
76
Решение.
Иррациональное выражение под знаком интеграла содержит корни с разными
показателями. Поэтому делается замена переменной:
,2
m
tx =−
где
.6)6,3,2( == HOKm
=
+
−
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
−=
=
+=
=−
=
∫
dt
tt
ttt
xt
dttdx
tx
tx
J
23
53
6
5
6
6
2
6)4(
2
6
,2
,2
=
+
−
=
∫
dt
t
tt
2
4
6
46
(Выделим целую часть)
=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++−+−+−=
=
⎟
⎠
⎞
⎜
⎝
⎛
+
+−+−+−
∫
ctttt
t
tt
dt
t
ttttt
2ln2401203010
4
15
5
8
3
2
6
2
240
120603015846
23
4
56
2345
−−+−−−+−−−
3
3
2
6
5
2180260)2(
2
45
)2(
5
48
)2(4 xxxxx
.22ln14402720
66
cxx ++−+−−
6.4. (в)
∫
+− 1cos2sin3 xx
dx
Решение.
Для интегрирования тригонометрического выражения, стоящего под знаком
данного интеграла, используется универсальная тригонометрическая подстановка,
которая сводит указанный интеграл к интегралу от рациональной дроби.
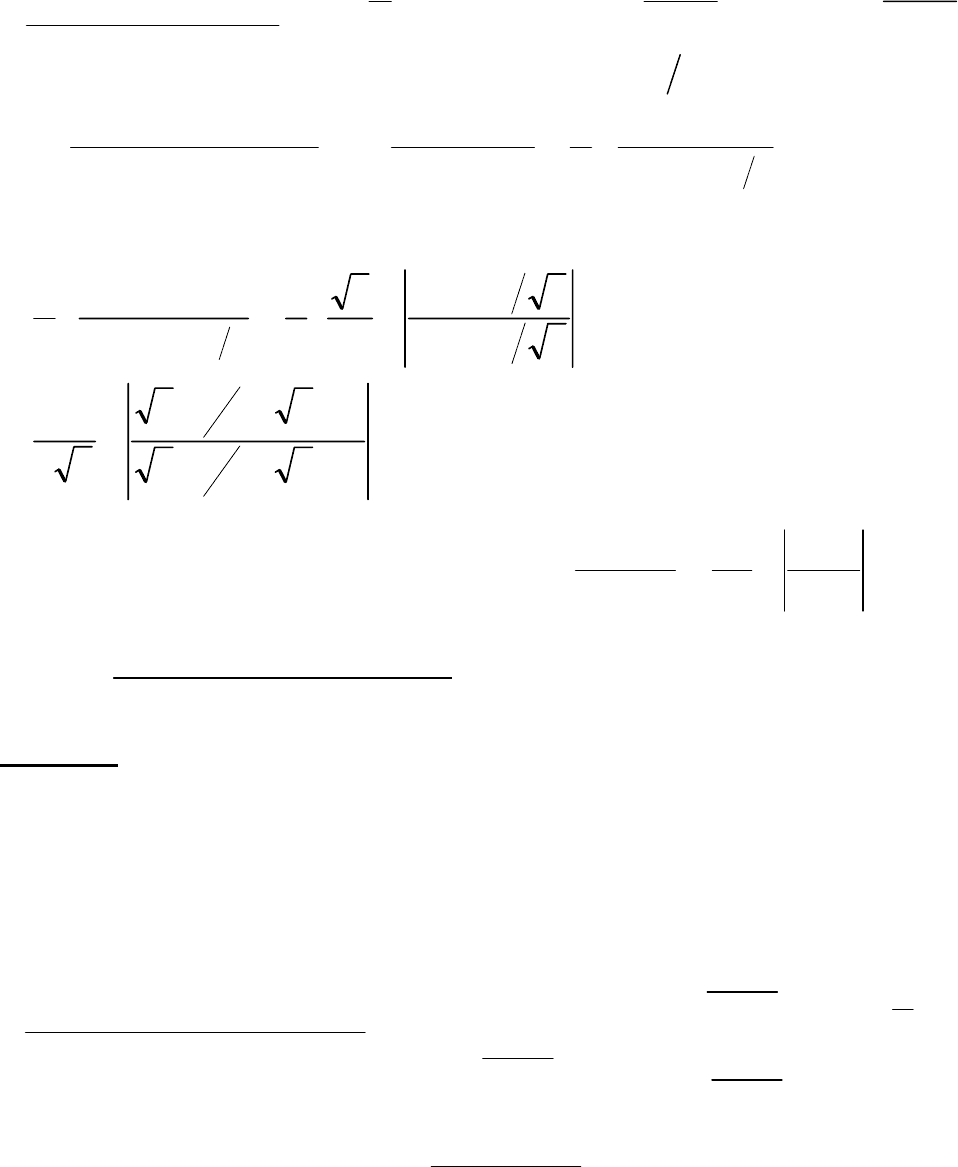
77
()
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
+
=
+=
+
−
=
=
=
=
+−
∫
2
2
2
2
1
2
,12sin
,
1
1
cos
,2
,
2
1cos2sin3
t
dt
dx
ttx
t
t
x
arctgtx
t
x
tg
xx
dx
∫∫∫
=
−+
=
−+
=
+++−
=
3123
2
163
2
1226
2
2222
tt
dt
tt
dt
ttt
dt
(В знаменателе выделим полный квадрат)
.
23
2
3
23
2
3
ln
32
1
321
321
ln
4
3
3
2
34)1(3
2
2
c
x
tg
x
tg
c
t
t
t
dt
+
++
−+
=
=+
++
−+
⋅=
−+
=
∫
(При интегрировании использовали формулу:
∫
+
+
−
=
−
c
au
au
aau
du
ln
2
1
22
).
6.4. (г)
.
cos32sinsin2
22
∫
+− xxx
dx
Решение.
Для интегрирования тригонометрической функции, четной относительно
xcos
и
xsin
, делается замена
t
tgx
=
, которая сводит данный интеграл к
интегралу от рациональной дроби.
=
⎪
⎪
⎭
⎪
⎪
⎬
⎫
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
+
=
+
=
+
=
=
=
+−
∫
tdtdx
t
x
t
t
x
t
dt
dx
ttgx
xxx
dx
3
2
,
1
1
cos
,
1
sin
,
1
,
cos32sinsin2
2
2
2
2
2
2
22
∫
=
+−
=
322
2
tt
dt
(В знаменателе выделим полный квадрат)
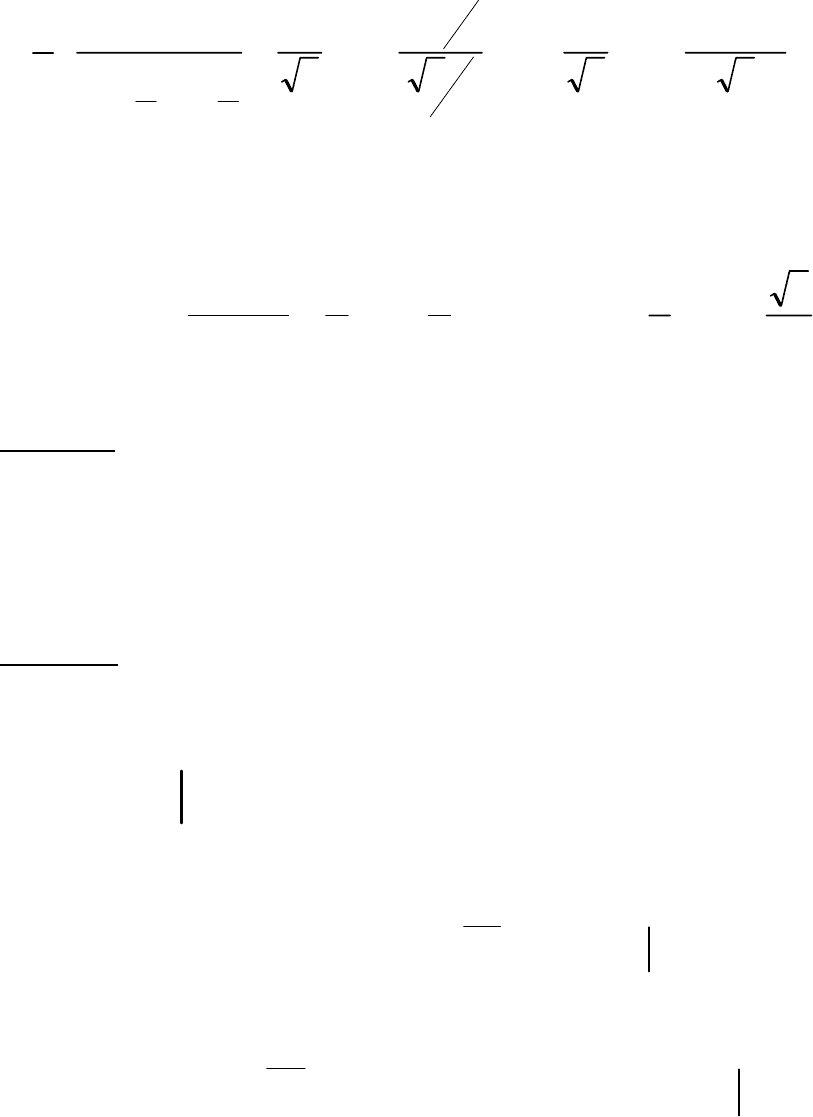
78
∫
+
−
=+
−
=
+
⎟
⎠
⎞
⎜
⎝
⎛
−
= .
5
12
5
1
2
5
2
1
5
1
4
5
2
1
2
1
2
c
tgx
arctgc
t
arctg
t
dt
При
интегрировании использовали формулу:
∫
+=
+
,
1
22
c
a
u
arctg
aau
du
.
2
5
,
2
1
=−= atu
Задача 7.
Вычислить определенный интеграл
7(а).
.ln
1
2
∫
e
xdx
Решение.
Используем формулу интегрирования по частям для определенного интеграла:
.
∫∫
−=
b
a
b
a
b
a
vduuvudv
=−=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
=
=
=
=
=
∫∫
e
e
e
xdxxx
xv
x
dx
xdu
dxdv
xu
xdx
1
1
2
2
1
2
ln2ln
,
,ln2
,
,ln
ln
=−−−=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
=
=
=
=
=
e
xxxee
xv
x
dx
du
dxdv
xu
1
22
)ln(21lnln
,
,
,
,ln
.222ln2
−
=−+−= eeeee
(При решении данного примера формула интегрирования по частям была
использована дважды).
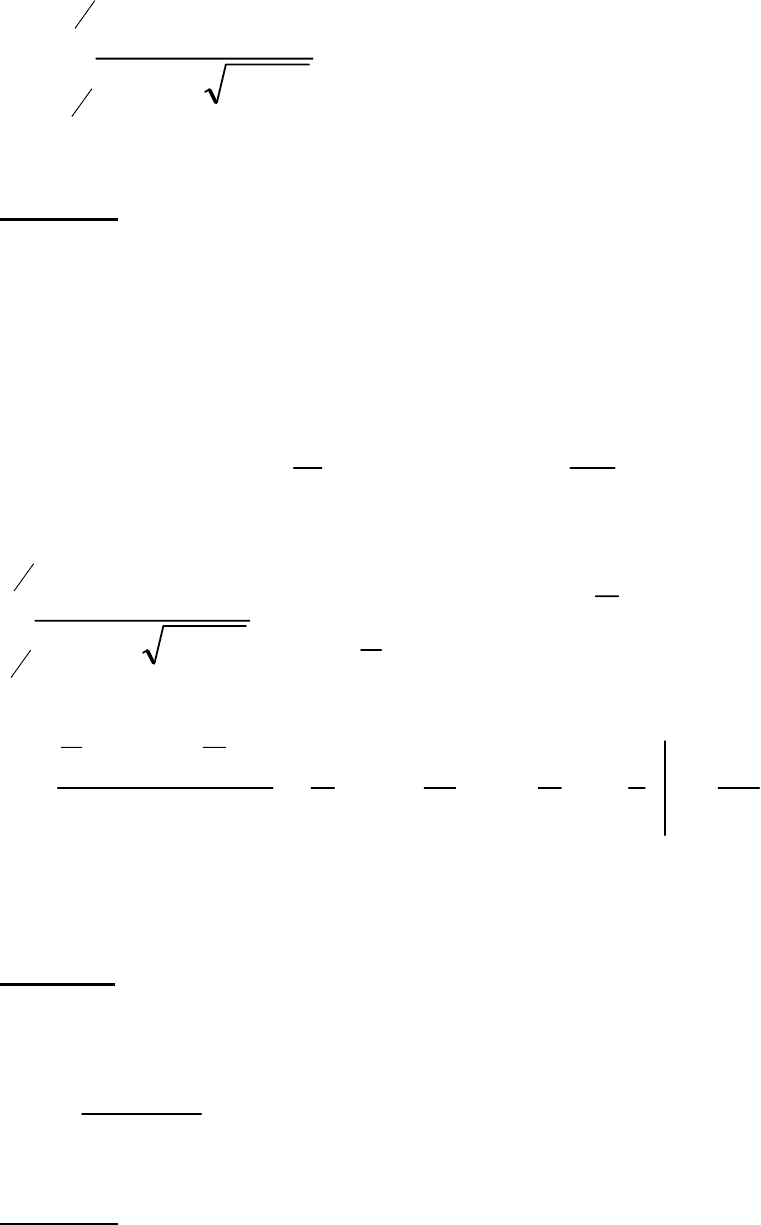
79
7(б).
∫
−−
3
10
3
2
13)13( xx
xdx
Решение.
Данный интеграл приводится к интегралу от рациональной функции с помощью
подстановки
.13
2
tx =−
С помощью этой же подстановки пересчитаваются
пределы интеграла [4]:
.3
3
10
;1
3
2
=⇒==⇒= txtx
.
27
161
9
21
1
9
2
3
2
)1(
3
1
3
2
),1(
3
1
,13
13)13(
3
1
3
1
2
3
1
2
2
3
10
3
2
2
2
=
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
+=
⋅
⋅+
=
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
=
+=
=−
=
−−
∫∫
∫
t
tdt
ttt
tdtt
tdtdx
tx
tx
xx
xdx
Замечание. При интегрировании рациональной дроби выполнено почленное
деление числителя на знаменатель.
Задача 8.
Вычислить несобственный интеграл или исследовать его на сходимость.
8.1.
∫
∞
+
0
3
)1(x
xdx
Решение.
Несобственный интеграл первого рода (по бесконечному промежутку) от
правильной рациональной дроби может быть вычислен согласно определению
несобственного интеграла первого рода [4].
80
.
2
1
2
111
2
1
1
)1(2
1
1
1
lim
)1(2
1
1
1
lim
)1()1(
lim
)1(
1)1(
lim
)1(
2
0
2
00
32
0
3
0
3
=+
∞
+
∞
−=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
+
+
+
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
+
−=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
+
=
+
−+
=
+
∞→∞→
∞→∞→
∞
∫∫∫∫
αα
α
α
α
αα
α
α
α
xx
x
dx
x
dx
dx
x
x
x
xdx
Несобственный интеграл сходится и его значение равно
2
1
.
8.2.
.
34
1
0
2
∫
+− xx
dx
Решение.
Подынтегральная функция
)3)(1(
1
34
1
)(
2
−−
=
+−
=
xxxx
xf
разрывна в точках
1=x
и
3=x
.
Данный интеграл является несобственным интегралом второго рода, так как
верхний предел совпадает со значением
х=1.
[]
,
1
3
lnlim
2
1
1ln3lnlim
2
1
1
1
3
1
2
1
lim
)3)(1(
)3()1(
2
1
)3)(1(
1
0
0
1
0
0
1
0
0
1
0
1
0
∞=
−
−
=−−−=
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
−
=
−−
−−−
=
−−
−
→
−
→
−
→
∫∫∫
ε
ε
ε
ε
ε
ε
x
x
xx
dx
xx
dx
xx
xx
xx
dx
то есть несобственный интеграл расходится.
8.3.
∫
−
4
0
3
3x
dx
