Циценкова Г.А., Чукавина Т.В., Рязанова Л.Д., Труппова В.А. Методические указания и контрольные задания по высшей математике
Подождите немного. Документ загружается.

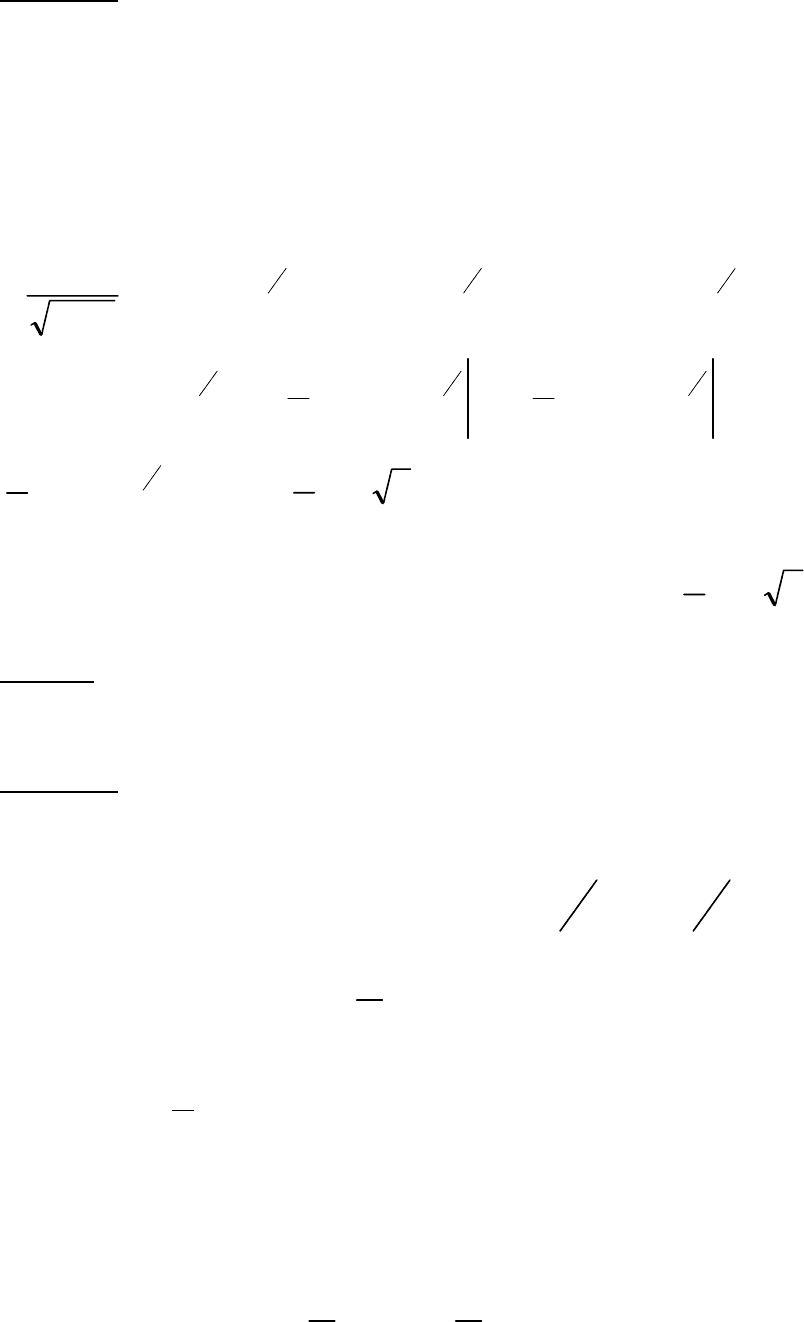
81
Решение.
Подынтегральная функция разрывна в точке х=3 и эта точка принадлежит
отрезку интегрирования. Поэтому интеграл разбивается на два, чтобы особая
точка в каждом из них была в конце интервала интегрирования [4].
(
)
).91(
2
3
01)3(0
2
3
)3(lim
2
3
)3(lim
2
3
)3(lim
)3(lim)3()3(
3
3
3
2
4
3
3
2
0
4
3
3
0
3
2
0
3
1
0
3
0
3
1
0
4
3
3
1
3
0
3
1
4
0
3
−=−+−−
=−+−=−+
+−=−+−=
−
+
→
+
−
→
−
→
−
−
→
−−
∫
∫∫∫∫
ε
ε
ε
ε
εε
ε
ε
xxdxx
dxxdxxdxx
x
dx
Несобственный интеграл сходится и его значение равно
).91(
2
3
3
−
Задача.
Вычислить площадь фигуры, ограниченной линией
.3cos2
ϕ
ar
=
Решение.
В полярной системе координат уравнением
ϕ
3cos2ar
=
задается
трехлепестковая роза. Для одного лепестка
.
66
π
ϕ
π
≤≤−
При
;2,0 ar ==
ϕ
при
.0,
6
=±= r
π
ϕ
Искомая площадь находится по
формуле
∫
=
2
1
,
2
1
2
ϕ
ϕ
ϕ
drS
1
ϕ
и
2
ϕ
- корни уравнения
.0)(
=
ϕ
r
Для нашей задачи это уравнение примет вид:
.
6
,
2
3,03cos2
π
ϕ
π
ϕϕ
±=±==a
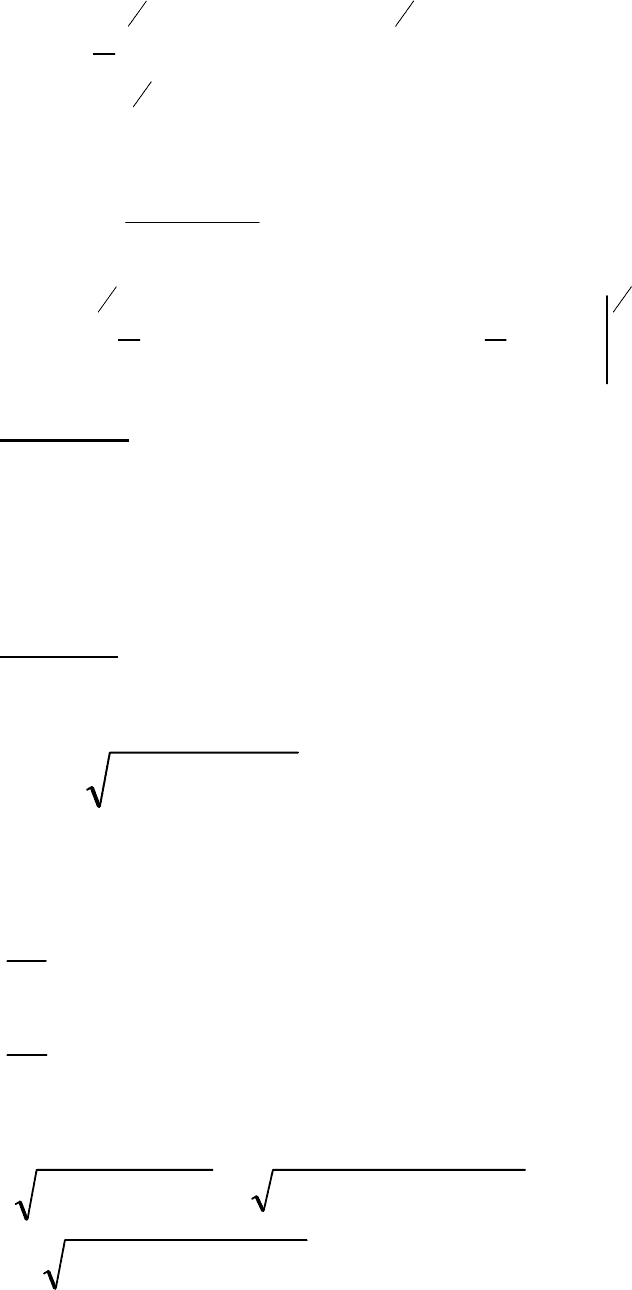
82
Учитывая симметрию, записываем:
∫∫
−
==⋅=
6
6
6
0
2222
3cos433cos4
2
1
3
π
π
π
ϕϕϕϕ
dadaS
= (подынтегральную функцию преобразуем с помощью формулы
2
2cos1
cos
2
α
α
+
=
=
∫
=
⎟
⎠
⎞
⎜
⎝
⎛
+=+=
6
0
2
6
0
22
.6sin
6
1
6)6cos1(
2
1
12
π
π
πϕϕϕϕ
aada
Задача 10.
Вычислить длину линии
⎩
⎨
⎧
≤≤
+−=
+−=
.0
,sin2cos)2(
,cos2sin)2(
2
2
π
t
tttty
ttttx
Решение.
Длина дуги линии, заданной параметрически, определяется по формуле [4]:
.)()(
2
1
22
dtyxl
t
t
tt
∫
′
+
′
=
Находим подынтегральную функцию.
.sincos2sin2sin)2(cos2
.cossin2cos2cos)2(sin2
22
22
ttttttttty
dt
dy
tttttttttx
dt
dx
t
t
=++−−−=
′
=
=−+−+=
′
=
Тогда
.)sin(cos
sincos)()(
2224
242422
tttt
ttttyx
tt
=+=
=+=
′
+
′
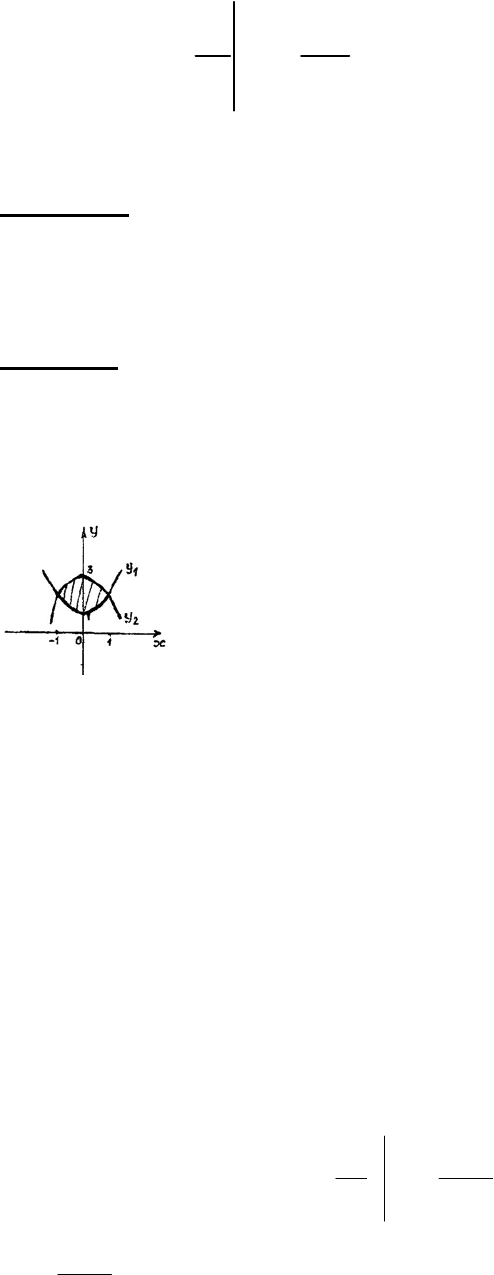
83
.)(
33
3
0
0
3
2
ед
t
dttl
π
π
π
===
∫
Задача 11.
Вычислить объем тела, полученного вращением вокруг оси
X
0 плоской фигуры,
ограниченной параболами
1 ,3
22
+=−= xyxy
.
Решение.
Находим точки пересечения параболы:
).2,1();2,1(
21
MM
−
Объем данного тела получаем как разность объемов
.
12
VV
−
.3
;1
2
2
2
1
xY
xY
−=
+=
.)1(
;)3(
1
1
222
11
1
1
222
22
∫∫
∫∫
−
−
+==
−==
b
a
b
a
dxxdxyV
dxxdxyV
ππ
ππ
[]
()
.
3
32
.
3
32
3
8)88(
)1()3(
3
1
1
1
1
3
2
1
1
2222
12
eдV
x
xdxx
dxxxVVV
π
π
ππ
π
=
=
⎟
⎠
⎞
⎜
⎝
⎛
−=−=
=+−−=−=
∫
∫
−
−
−
84
Контрольная работа №3
Раздел 1. Дифференциальные уравнения
Вопросы для самоподготовки
1. Дайте определения дифференциального уравнения первого порядка и его
общего и частного решений (интегралов). Сформулируйте задачу Коши
для дифференциального уравнения первого порядка и укажите ее
геометрический смысл.
2.
Сформулируйте теорему о существовании и единственности решения
дифференциального уравнения первого порядка. Найдите общее решение
уравнения и укажите область, где условия этой теоремы не выполняются.
3.
Дайте определение дифференциальных уравнений первого порядка: с
разделяющимися переменными, однородного, линейного и уравнения
Бернулли. Изложите методы нахождения их общих решений. Приведите
примеры.
4.
Дайте определение дифференциальных уравнений второго порядка,
допускающих понижение порядка. Изложите методы нахождения их
общих решений. Приведите примеры.
5.
Дайте определение линейного неоднородного дифференциального
уравнения второго порядка с постоянными коэффициентами. Изложите
метод нахождения общего решения однородного уравнения и метод
неопределенных коэффициентов для нахождения частного решения
неоднородного уравнения. Запишите общее решение неоднородного
уравнения. Приведите примеры.
6.
Изложите метод решения систем линейных дифференциальных уравнений
с постоянными коэффициентами. Приведите пример.
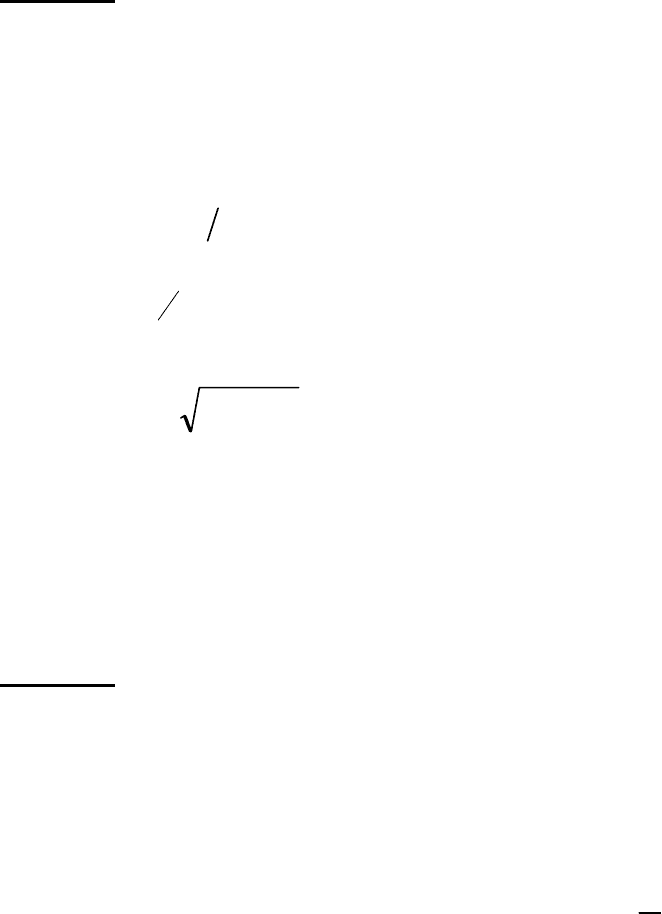
85
Контрольные задания
Задача 1.
Найти общее решение дифференциального уравнения первого порядка.
1.1.
()
xyyyx 2
22
=
′
−
1.2.
(
)
222
)1(21 xxyyx +=−
′
+
1.3.
)ln( xyyyx =
′
1.4.
3
=
+
′
yyx
1.5.
0=−+
′
yxeyx
x
y
1.6.
xyxy sin)1(cos +
=
′
1.7.
22
yxyyx +=−
′
1.8.
32
2
=−
′
xyyx
1.9.
02
22
=−+
′
xyyyx
1.10.
1+
=
+
′
xyyx
Задача 2.
Найти общее решение дифференциального уравнения второго порядка,
допускающие понижение порядка.
2.1.
()
yxyx
′
=
′′
−
2
1
2.2.
0)()(2
42
=
′
+
′
+
′′
yyyy
2.3.
xtgxyy 2sin=
′
+
′′
2.4.
2
1
xy
x
y =
′
+
′′
2.5.
0)(1
2
=
′′
+
′
+ yyy
2.6.
(
)
0)(51
2
=
′
−
′′
+ yyy
2.7.
3
2 xyyx =
′
+
′′
2.8.
2
)(2 ytgyy
′
=
′′
2.9.
xtgxyy sin2 =
′
−
′′
2.10.
0)(3
2
=
′
+
′′
yyy
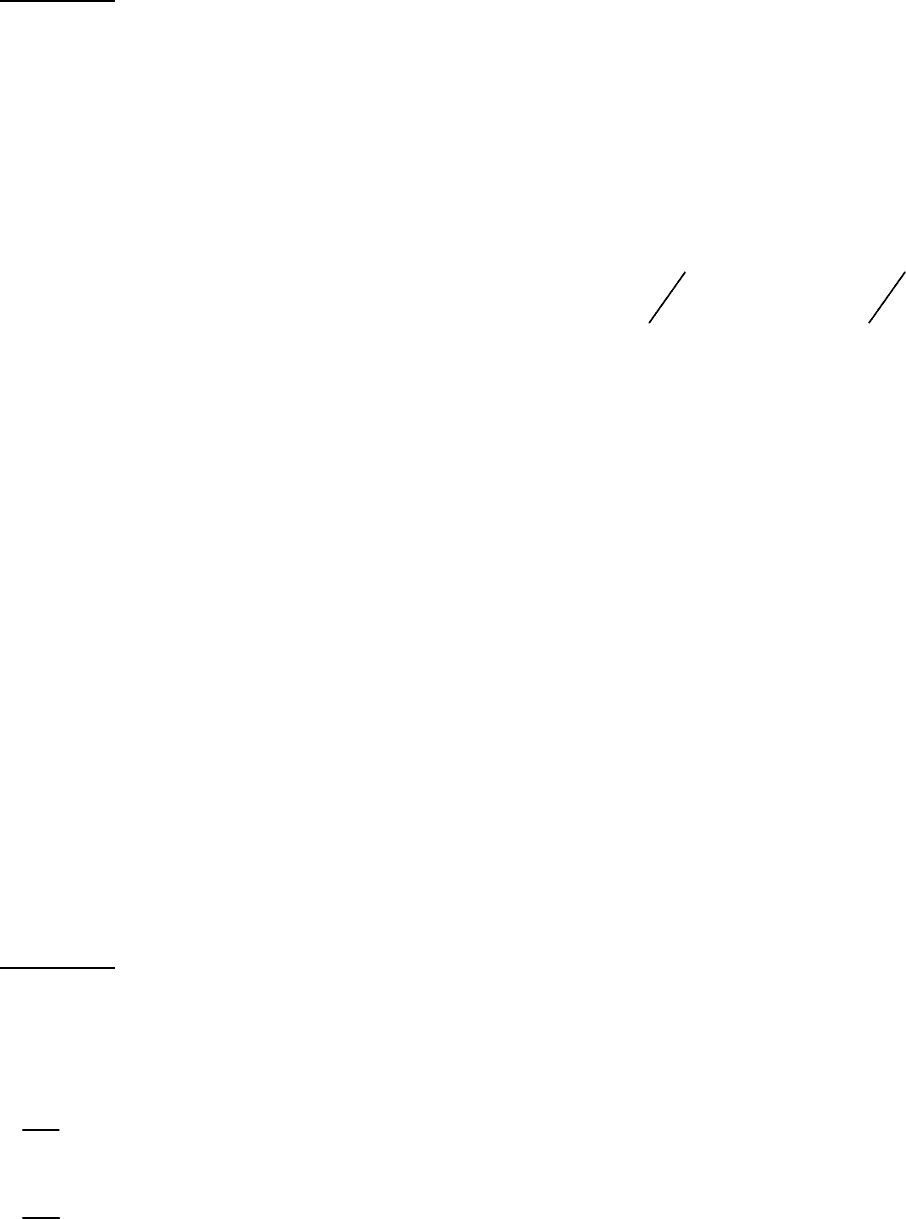
86
Задача 3.
Найти частное решение дифференциального уравнения
)(xfgyypy =+
′
+
′′
, удовлетворяющего начальным условиям
0
)0( yy
=
,
0
)0( yy
′
=
′
.
3.1.
xyyy 2sin8124
=
−
′
+
′′
0)0(
=
y
0)0(
=
′
y
3.2.
396
2
+−=+
′
−
′′
xxyyy
3
4
)0( =y
27
1
)0( =
′
y
3.3.
x
eyy
2
4
−
=+
′′
0)0(
=
y
0)0(
=
′
y
3.4.
x
xeyyy
2
52 =+
′
−
′′
1)0(
=
y
0)0(
=
′
y
3.5.
xyyy 2cos1265
=
+
′
+
′′
1)0(
=
y
3)0(
=
′
y
3.6.
x
exyyy
−
−=+
′
−
′′
)712(65
0)0(
=
y
0)0(
=
′
y
3.7.
526134 +
=
+
′
−
′′
xyyy
1)0(
=
y
0)0(
=
′
y
3.8.
164
2
+=
′
−
′′
xyy
2)0(
=
y
3)0(
=
′
y
3.9.
x
eyyy 162 =+
′
−
′′
1)0(
=
y
2)0(
=
′
y
3.10.
x
eyyy
3
1096
−
=+
′
+
′′
3)0(
=
y
2)0(
=
′
y
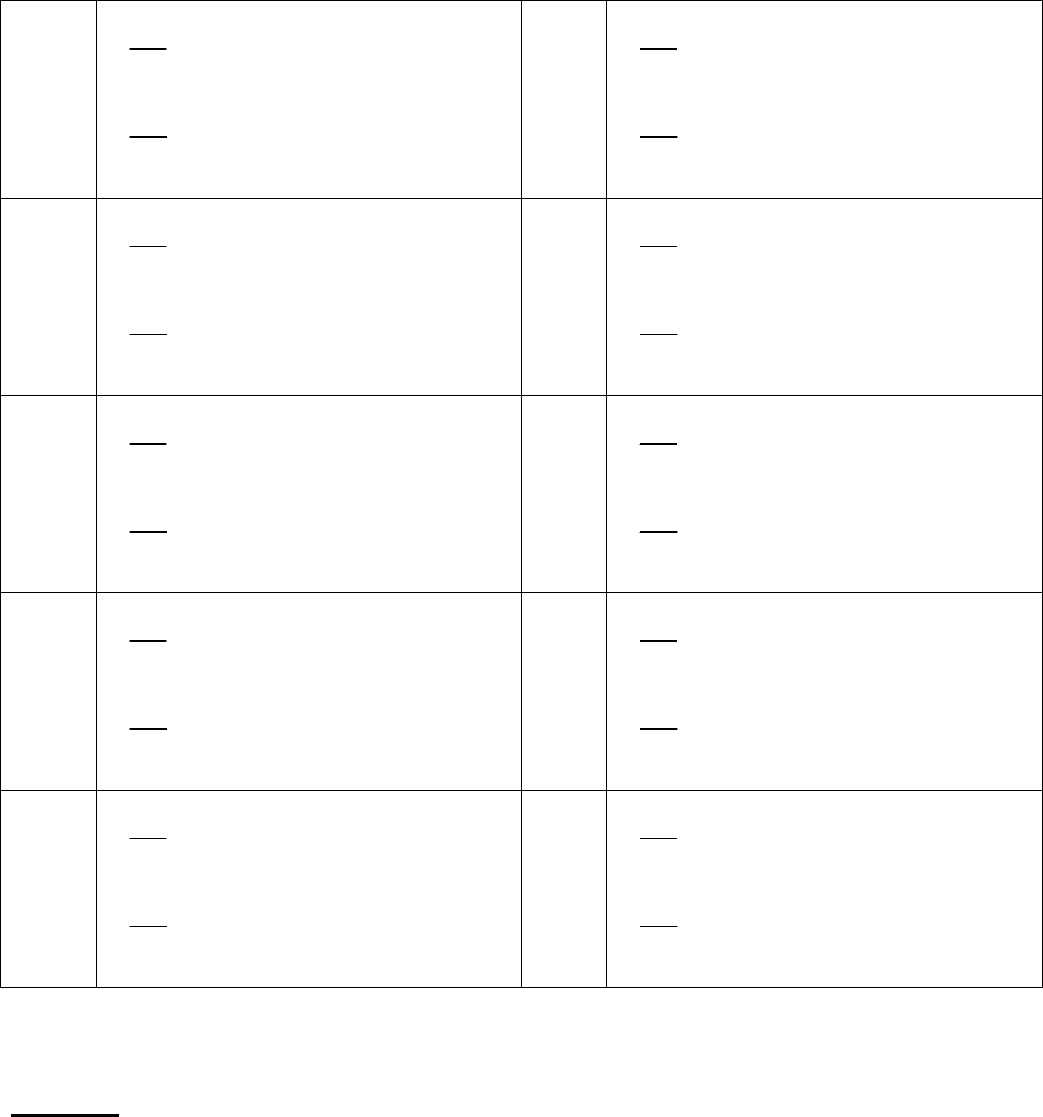
Задача 4.
Дана система линейных дифференциальных уравнений с постоянными
коэффициентами.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+=
+=
.
,
2221
1211
yaxa
dt
dy
yaxa
dt
dx
87
Требуется: 1) найти общее решение системы с помощью
характеристического уравнения; 2) записать данную систему и ее решение в
матричной форме.
4.1.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+=
+=
.24
,64
yx
dt
dy
yx
dt
dx
4.2.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−−=
−−=
.32
,45
yx
dt
dy
yx
dt
dx
4.3.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+=
+=
.8
,3
yx
dt
dy
yx
dt
dx
4.4.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−−=
+=
.58
,36
yx
dt
dy
yx
dt
dx
4.5.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+=
+−=
.3
,5
yx
dt
dy
yx
dt
dx
4.6.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+=
−=
.82
,23
yx
dt
dy
yx
dt
dx
4.7.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−−=
−−=
.24
,64
yx
dt
dy
yx
dt
dx
4.8.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−−=
−−=
.33
,85
yx
dt
dy
yx
dt
dx
4.9.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−−=
−−=
.37
,5
yx
dt
dy
yx
dt
dx
4.10.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−=
+−=
.84
,57
yx
dt
dy
yx
dt
dx
Решение типового варианта
Задача 1
Найти общее решение дифференциальных уравнений первого порядка:
а)
;0)( =
+
+
′
+ yxyyxxy
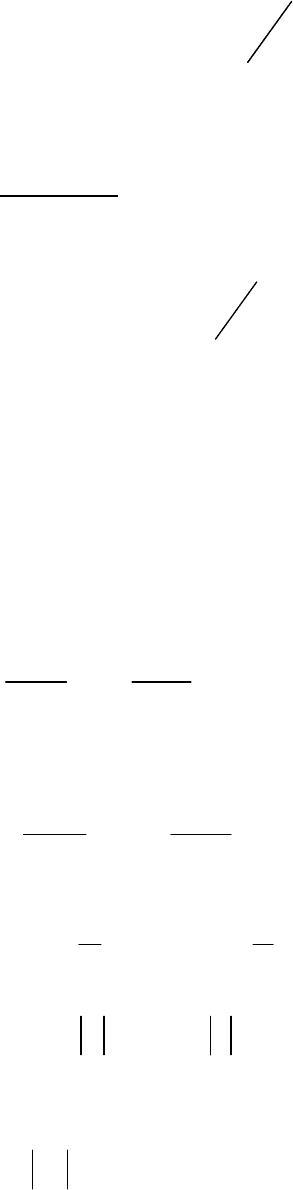
88
б)
;ln1
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+=
′
x
y
yyx
в)
.cos
2
xxyyx =−
′
Решение.
а)
;0)( =
+
+
′
+ yxyyxxy
Заменим
y
′
на
dx
dy
и, умножив обе части уравнения на
dx
, получим:
.0)()( =+++ dxyxydyxxy
Отсюда имеем:
.0)1()1( =+++ dxxydyyx
Мы получим уравнение с разделяющимися переменными, разделив обе части
уравнения на
)0( ≠xy
, получим уравнение с разделенными переменными [3]:
.0
11
=
+
+
+
dx
x
x
dy
y
y
Интегрируем:
∫∫
=
+
+
+
;
11
cdx
x
x
dy
y
y
∫∫
=
⎟
⎠
⎞
⎜
⎝
⎛
++
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+ ;
1
1
1
1 cdx
x
dy
y
cxxyy lnlnln =+++
Используя свойства логарифмов,
,lnlnln ,ln xyyxeyx
yx
=+=+
+
получим
,lnlnln cexy
yx
=+
+
общее решение.
.ceyx
yx
=⋅⋅
+
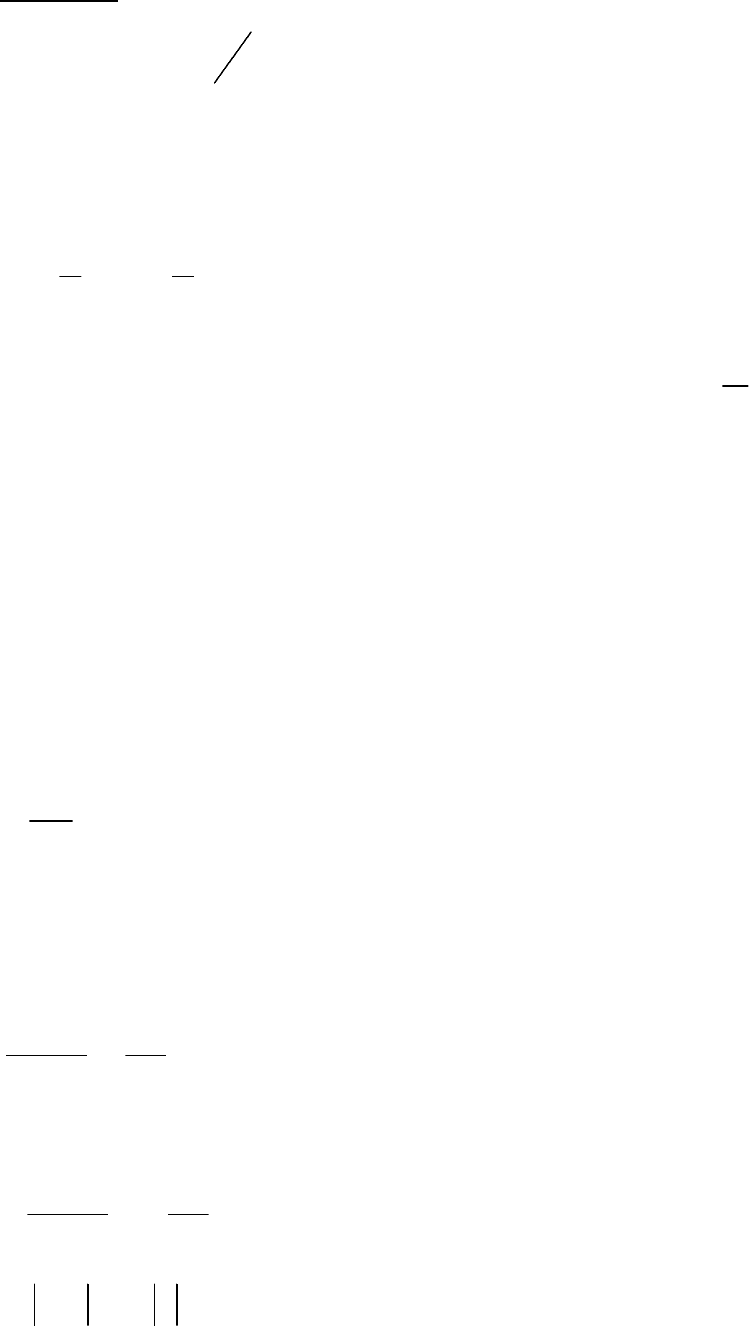
89
Решение.
б)
.ln1
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+=
′
x
y
yyx
Разрешив данное уравнение относительно
y
′
, мы получим однородное
дифференциальное уравнение [2]
.ln1
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+=
′
x
y
x
y
y
Однородные уравнения решаются с помощью подстановки
()
, , xuuu
x
y
==
,
то есть
uxy =
,
uxuy +
′
=
′
[3].
После подстановки
y
и
y
′
в уравнение получим
),ln1( uuuxu +=+
′
,ln uuuuxu +=+
′
,ln uuxu =
′
,ln uu
dx
du
x =
.ln udxuxdu =
Разделим переменные
).0ln(:
≠
uxu
и получим
.
ln
x
dx
uu
du
=
Проинтегрируем
∫∫
=
x
dx
uu
du
ln
, отсюда
,lnlnlnln cxu +=

90
,ln cxu =
тогда
,
cx
eu =
заменим
x
y
u =
, получим
,
cx
e
x
y
=
общее решение.
.
cx
xey =
Решение
в)
.cos
2
xxyyx =−
′
Разрешим данное уравнение относительно
.cos: xx
x
y
yy =−
′′
Мы получили линейное дифференциальное уравнение вида
).()( xQyxPy
=
+
′
Здесь
,
1
)(
x
xP −=
.cos)( xxxQ =
Используя метод Бернулли, положим
),()( xxuy
ν
=
тогда
ν
ν
′
+
′
=
′
uuy
Подставим
y
и
y
′
в уравнение
,cos xx
x
u
uu =−
′
+
′
ν
νν
.cos xx
x
uu =
⎟
⎠
⎞
⎜
⎝
⎛
−
′
+
′
ν
νν
Так как выражение
ν
⋅= uy
представляет произведение двух функций, то одну
из функций можно выбрать произвольно. Выберем
ν
так, чтобы
.0=−
′
x
ν
ν
Имеем уравнение с разделяющимися переменными
,0=−
xdx
d
ν
ν
