Циценкова Г.А., Чукавина Т.В., Рязанова Л.Д., Труппова В.А. Методические указания и контрольные задания по высшей математике
Подождите немного. Документ загружается.

31
7.2.
⎪
⎩
⎪
⎨
⎧
>+−
≤<−+
−≤+
=
.1,3
;11,1
;1,2
)(
2
xx
xx
xx
xf
7.3.
⎪
⎩
⎪
⎨
⎧
≥−
<<−−
≤−
=
.2,3
;20,)12(
;0,
)(
2
xx
xx
xx
xf
7.4.
⎪
⎩
⎪
⎨
⎧
≥
<<+
≤
=
.1,
;10,1
;0,cos
)(
2
xx
xx
xx
xf
7.5.
⎪
⎩
⎪
⎨
⎧
>+
≤<
≤−
=
.2,1
;20,
;0,
)(
2
xx
xx
xx
xf
7.6.
⎪
⎩
⎪
⎨
⎧
>−
≤<
≤−
=
.,2
;0,sin
;0,
)(
π
π
xx
xx
xx
xf
7.7.
⎪
⎩
⎪
⎨
⎧
>
≤<−+
−≤+−
=
.0,
;01,)1(
;1),1(
)(
2
xx
xx
xx
xf
32
7.8.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<
≤−
=
.
4
,2
;
4
0,
;0,
)(
2
π
π
x
xtgx
xx
xf
7.9.
⎪
⎩
⎪
⎨
⎧
>
≤<+
≤−
=
.1,2
;10,1
;0,2
)(
2
x
xx
xx
xf
7.10.
⎪
⎩
⎪
⎨
⎧
≥
<<
≤−
=
.4,1
;40,
;0,2
)(
x
xx
xx
xf
Задача 8.
Найти производные
dx
dy
данных функций.
8.1.
а)
1
3
342
3
++
−+=
xx
xy
;
б)
2cos
)3( +=
x
ey
;
в)
)52sin(ln += xy
;
г)
x
x
xy =
;
д)
x
x
y
tg 5=
.
8.2.
а)
22
1 xxy −=
;
б)
x
x
y
2
cos
sin4
=
;
в)
x
arctgey
2
=
;
г)
x
xy
1
=
;
д)
0=+− arctgyyx
.
33
8.3.
а)
2
2
1
1
x
x
xy
−
+
=
;
б)
xtg
y
2
1
2
=
;
в)
xy 31arcsin −=
;
г)
x
xy
ln
=
;
д)
()
yxxy −= cossin
.
8.4.
а)
2
543
63
xx
x
y
+−
+
=
;
б)
xxxy cossin
−
=
;
в)
xxy
m
ln⋅=
;
г)
tgx
xy
−
=
;
д)
y
x
arctg
x
y
=
.
8.5.
а)
22
xa
x
y
−
=
;
б)
x
x
y
2
2
cos32
sin
+
=
;
в)
1
ln
−
=
x
xx
y
;
г)
x
arctgxy
ln
)(=
;
д)
01)1)(1( =−−−
yx
ee
.
8.6.
а)
5
3
2
15
1
1
++
+
= x
x
y
;
б)
)1(2
23
+= xtgy
;
в)
3
3
arctgx
y =
;
г)
x
arctgxy )(=
;
д)
x
y
exy =
2
.
34
8.7.
а)
3
2
2
1
1
x
x
y
−
+
=
;
б)
x
xxy )(
2
+=
;
в)
11
2
+−
=
x
x
arctgy
;
г)
xxtgy cosln
2
1
2
+=
;
д)
03
33
=−+ axyyx
.
(
)
consta
=
8.9.
а)
5
2
15 xxxy ++=
;
б)
xx
ey
−
= 2
;
в)
2
1/)(arcsin xxy −=
;
г)
x
xy )(cos=
;
д)
)/(ln yxarctgy =
.
8.10.
а)
3
32
11 +++= xxy
;
б)
tgxxtgy −=
3
3
1
;
в)
)2/()3( −−= xxarctgy
;
г)
2
)(cos
x
xy =
;
д)
0=+− arctgxeyx
y
.
Задача 9.
Найти
dx
dy
и
2
2
dx
yd
для заданных функций. а)
)(xfy
=
; б)
)(tx
ϕ
=
;
)(ty
ψ
=
.
9.1.
а)
)1/(
2
−= xxy
;
б)
)2/cos(tx
=
;
tty sin−=
9.2.
а)
xctgy 2ln=
;
б)
ttx 8
3
+=
;
tty 2
5
+=
9.3.
а)
xxy ln
3
⋅=
;
б)
ttx sin
−
=
;
ty cos1 −=

35
9.4.
а)
arctgxxy ⋅=
;
б)
t
ex
2
=
;
t
y cos=
9.5.
а)
arctgxy =
;
б)
tx
2
cos3=
;
ty
3
sin2=
9.6.
а)
xctg
ey
3
=
;
б)
tx cos3
=
;
ty
2
sin4=
9.7.
а)
xey
x
cos=
;
б)
3
3 ttx −=
;
2
3ty =
9.8.
а)
xey
x
sin
−
=
б)
3
2 ttx −=
;
2
2ty =
9.9.
а)
2
1 xxy +=
б)
ttx cosln
+
=
;
tty sinln−=
.
9.10.
а)
2
x
exy
−
⋅=
б)
tx ln
=
;
⎟
⎠
⎞
⎜
⎝
⎛
+=
t
ty
1
2
1
.
Задача 10.
Найти наибольшее и наименьшее значения функции
)(xfy
=
на отрезке [а;в].
10.1.
712)(
3
+−= xxxf
;
[
]
3;0
.
10.2.
2)3/5()(
35
+−= xxxf
;
[
]
2;0
.
10.3.
(
)
xxxf cos23)( +⋅=
;
[
]
2
;0
π
.
10.4.
2163)(
34
+−= xxxf
;
[
]
1;3
−
.
10.5.
13)(
3
+−= xxxf
;
[
]
2;
2
1
.
10.6.
xxxf 4)(
4
+=
;
[
]
2;2
−
10.7.
(
)
xxxf sin23)( −⋅=
;
[
]
2
;0
π
36
10.8.
4
81)( xxxf −=
;
[
]
4;1
−
10.9.
2
23)( xxf −=
;
[
]
3;1
−
10.10.
xxxf sin)(
−
=
;
[
]
π
π
;
−
Задача 11.
Исследовать методами дифференциального исчисления функцию
)(xfy =
и,
используя результаты исследования, построить ее график.
11.1.
)4/(4
2
xxy +=
11.2.
)1/()1(
22
+−= xxy
11.3.
)1/()1(
22
−+= xxy
11.4.
)1/(
2
−= xxy
11.5.
)1/(
22
+= xxy
11.6.
xxy /)54(
3
+=
11.7.
)3/()5(
2
−−= xxy
11.8.
)1/(
34
−= xxy
11.9.
)1/(4
33
−= xxy
11.10.
)41/()42(
22
xxy −−=
Решение типового варианта.
Задача 6.1.
;
736
527
lim
24
24
∞
∞
=
−+
++
∞→
xxx
xx
x
Имеем неопределенность вида
∞
∞
[7]. Чтобы раскрыть ее, разделим числитель и
знаменатель дроби под знаком предела на высшую степень Х [7].
Получим
32
42
/7/36
/5/27
lim
xx
xx
x
−+
++
∞→
.
Применив теоремы о пределах [4], придем к равенствам
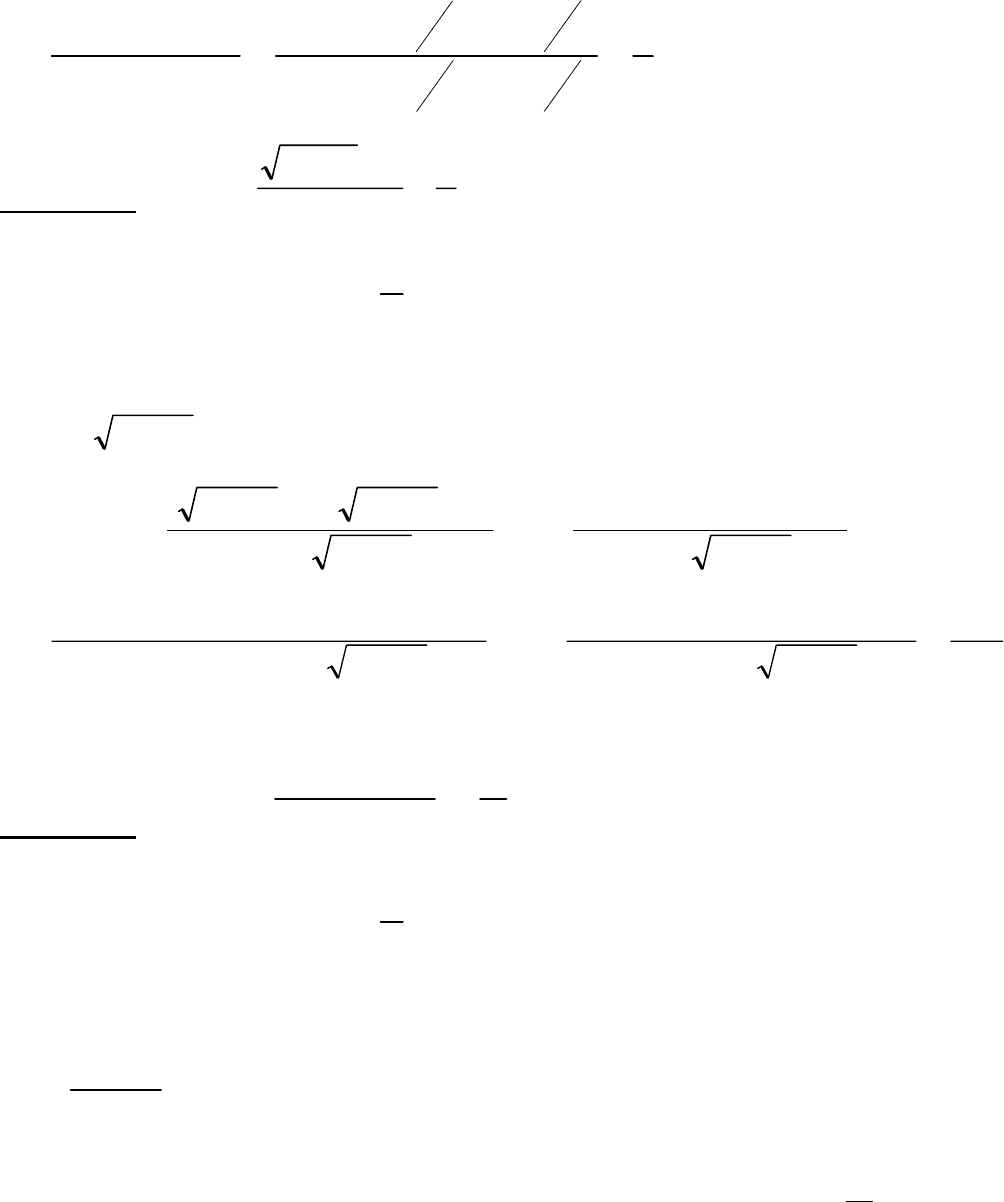
37
.
6
7
7
lim
3
lim6lim
5
lim
2
lim7lim
736
527
lim
32
42
24
24
=
−+
++
=
−+
++
∞→∞→∞→
∞→∞→∞→
∞→
xx
xx
xxx
xx
xxx
xxx
x
Задача 6.2.
;
0
0
64
521
lim
3
4
=
−
−+
→
x
x
x
Имеем неопределенность вида
0
0
[7]. Чтобы раскрыть ее, умножим числитель и
знаменатель дроби под знаком предела на выражение, сопряженное числителю,
т.е. на
(
)
521 ++ x
.
Получим
(
)
(
)
()
()
()
()
=
++−
−+
=
++−
++−+
→→
52164
2521
lim
52164
521521
lim
3
4
3
4
xx
x
xx
xx
xx
.
480
1
)521)(164(
1
lim
)521)(164)(4(
4
lim
2
4
2
4
=
++++
=
++++−
−
→→
xxxxxxx
x
xx
Задача 6.3.
;
0
03cos1
lim
2
0
=
−
→
x
x
x
Имеем неопределенность вида
0
0
. Раскроем ее, применив первый замечательный
предел [7]
.1
sin
lim
0
=
→
α
α
α
Числитель преобразуем с помощью формулы
.
2
sin2cos1
2
α
α
=−
Получим
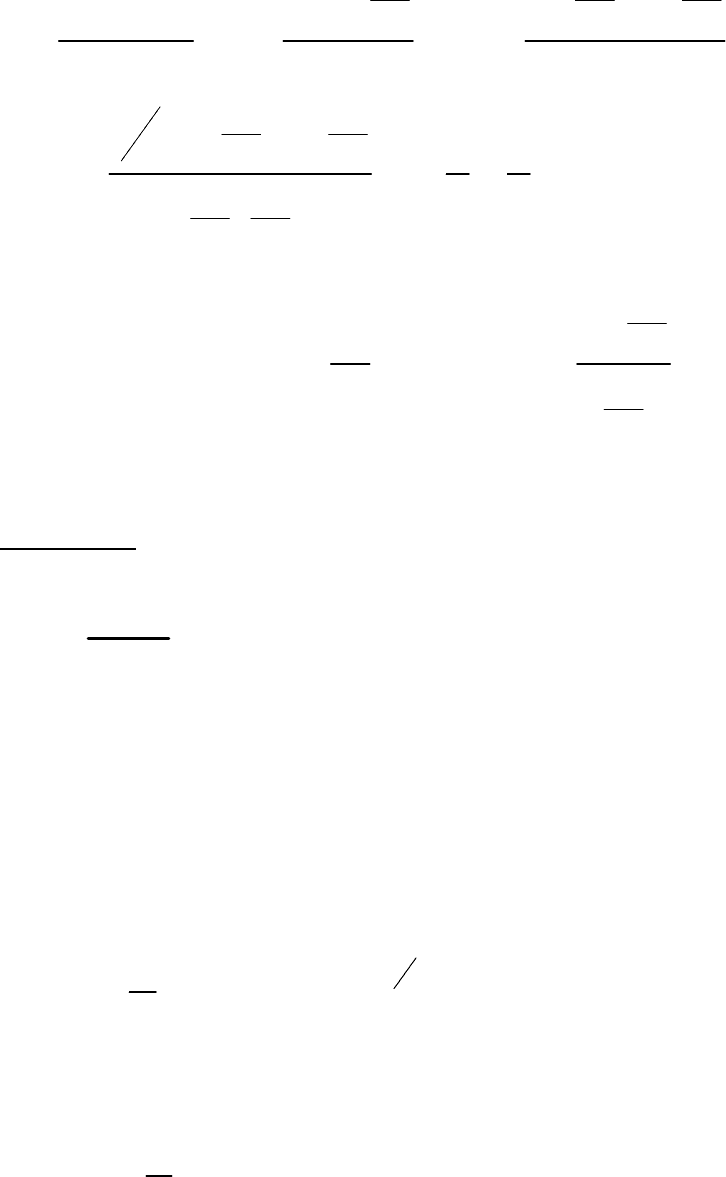
38
()
,
2
9
4
9
2
2
3
2
3
2
3
sin
2
3
sin
4
9
lim2
2
3
sin
2
3
sin
lim2
2
3
sin2
lim
3cos1
lim
0
0
2
2
0
2
0
=⋅=
⋅
⋅
=
=
⋅
⋅
==
−
→
→→→
xx
xx
xx
xx
x
x
x
x
x
xxx
так как при
.1
2
3
2
3
sin
lim0
2
3
0
0
=→=→
→
x
x
и
x
x
x
α
Задача 6.4.
;1
1
1
lim
∞
→∞
=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
x
x
x
x
В этой задаче предел основания равен 1 (разделите числитель и знаменатель на
Х),а показатель степени стремится к бесконечности; имеем неопределенность
вида
∞
1
.
Раскроем ее с помощью второго замечательного предела [5]:
.71828,2)1(lim
1
1lim
1
0
==+=
⎟
⎠
⎞
⎜
⎝
⎛
+
→∞→
e
x
x
x
α
α
α
Для этого представляем основание в виде
(
)
1
+
α
, а в показателе выделяем
множитель
α
1
:

39
.2
1
1
2
lim
)1(
2
2
1
1
2
2
1
1
2
1lim
1
2
1lim
1
2
1lim1
1
1
1lim
1
1
lim
ee
xx
xx
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
+=
⎟
⎠
⎞
⎜
⎝
⎛
−
+=
=
⎟
⎠
⎞
⎜
⎝
⎛
−
+=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
+=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
−
−−
∞→
−
⋅
−
∞→
∞→∞→∞→
∞→
Переходя к пределу в квадратной скобке, получим число е, согласно формуле, так
как
.0)1(2
∞
→→−= xприx
α
Задача 6.5.
[]
;)(ln)2ln()4(lim
∞
−
∞
=
∞
−
∞
∞
=−−−
∞→
xxx
x
Имеем неопределенность вида
∞
−
∞
. С помощью алгебраических
преобразований получим:
.2lnlnln
2
1limln
2
1limln
2
lnlim
2
ln)4(lim
2
)82(lim
82
lim
)4(
2
2
44
−====
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−=
=
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
−
⋅−
−
+−
+−
−−
−
∞→
−
∞→
−
∞→∞→
∞→
∞→
eee
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
При вычислении
4
2
1lim
−
∞→
⎟
⎠
⎞
⎜
⎝
⎛
−
x
x
x
имеем неопределенность
∞
1
, которую раскрыли с
помощью второго замечательного предела.
Задача 6.6.
;
0
0
3arcsin
2cos4cos
lim
2
0
=
−
→
x
xx
x
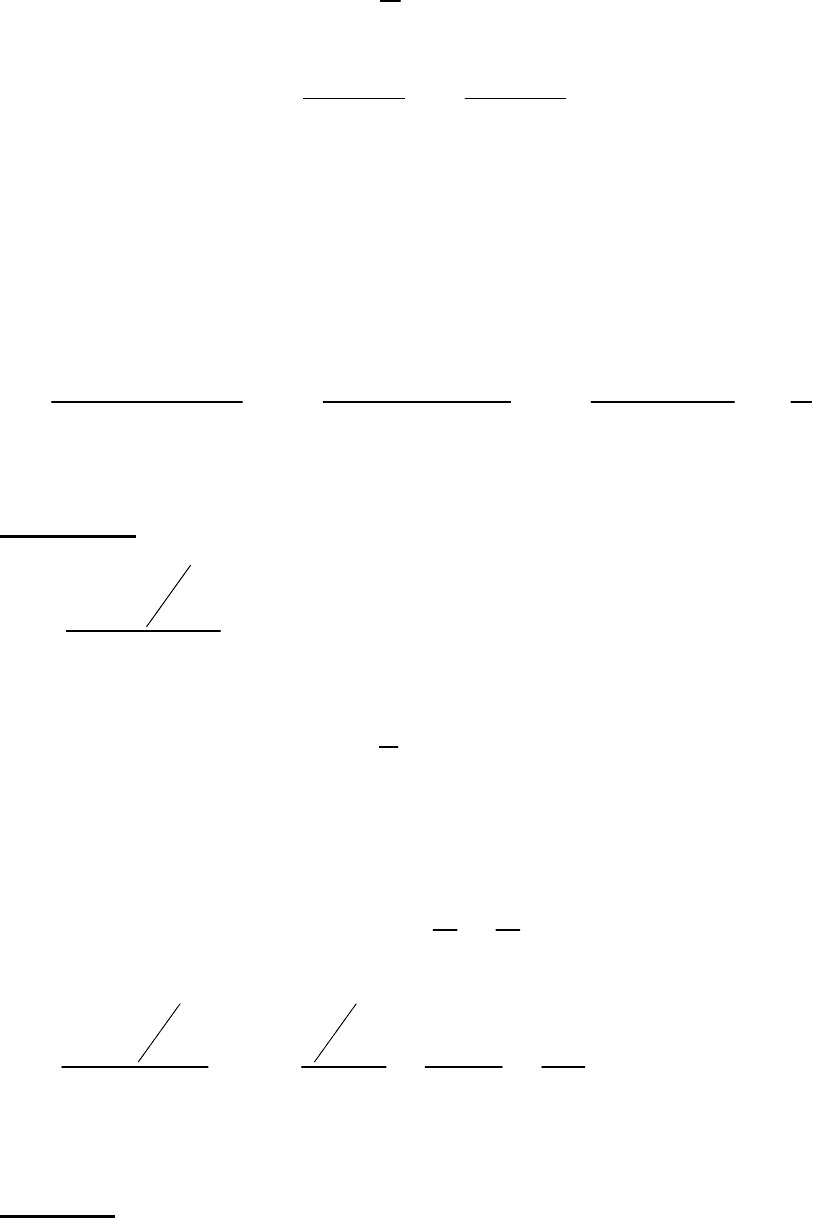
40
Имеем неопределенность вида
0
0
. По формуле тригонометрии, получим
.sin3sin2
2
24
sin
2
24
sin22cos4cos xx
xxxx
xx ⋅−=
−
⋅
+
−=−
При
,3~3arcsin,~sin,3~3sin0 xxxxxxx →
то есть
,)3(~)3(arcsin
22
xx
поэтому по теореме о замене эквивалентной
получим [4]
.
3
2
9
3)2(
lim
3arcsin
sin3sin2
lim
3arcsin
2cos4cos
lim
2
0
2
0
2
0
−=
⋅
⋅
−
=
⋅
−
=
−
→→→
x
xx
x
xx
x
xx
xxx
Задача 6.7.
(
)
.
4
4
lim
2
0
xxarctg
x
tg
x→
Имеем неопределенность вида
0
0
. Так как при
,~,~0
α
α
α
α
α
arctgtg→
то при
,4~4,
4
~
4
030 xxarctg
xx
tgxиx →→
поэтому
() ()
.
64
1
416
1
4
4
lim
4
4
lim
2
0
2
0
=
⋅
=
⋅
=
→→
xx
x
xxarctg
x
tg
xx
Задача 7.
Задана функция
