Чурилов Г.Н. Наноматериалы и нанотехнологии

Подождите немного. Документ загружается.

молекулами гораздо меньше энергии связи между атомами, входящими в со-

став молекулы. Соответственно площадь такого кластера равна:

44 nRRS





, (3)

Если в кластере содержится достаточно большое количество молекул, то

число молекул на поверхности такого кластера равно n





, (4)

Таким образом, доля “поверхностных” молекул F=n

/n равна:



 nF

, (5)

В то время как отношение числа “поверхностных” молекул (атомов) к

числу объемных n

равно:









, (6)

Немедленный вывод из (5) - большая количественная величина отно-

шения поверхности к объему. Например:F  0.4 для n = 10

, F  0.2 для n = 10

Так у плотно упакованного кластера из 20 атомов только один атом на-

ходится внутри объема. У кластеров из 100 атомов - не более 20.

Уравнение (5), конечно, подразумевает достаточно большие кластеры n 

100. Для малых кластеров n < 100 необходимо детальное знание структуры

кластера. В некоторых случаях, однако, рассматриваемая нами модель жидкой

капли для описания свойств кластера имеет смысл, даже если число атомов в

кластере очень мало. Это можно проиллюстрировать на примере кластеров,

образующих изомеры - различные молекулярные конфигурации данного хи-

мического соединения. Каждый изомер локально устойчив, поскольку соответ-

ствует минимальной энергии, однако он может перейти в другую изомерную

форму, если при нагревании получит достаточно энергии. Один из примеров

таких “текучих” кластеров - тример натрия: три атома образуют равнобедрен-

ный треугольник, у которого угол, образованный двумя одинаковыми сторо-

нами, не остается в каком-то одном положении, а непрерывно перемещается с

одной вершины на другую. Поскольку на микроскопическом уровне их форма

не фиксирована, текучие кластеры следует рассматривать в этом случае скорее

как капли жидкости, а не как твердые частицы.

Теоретическое и экспериментальное определение F может быть по-

лучено различными путями, включающими различные модели укладки частиц

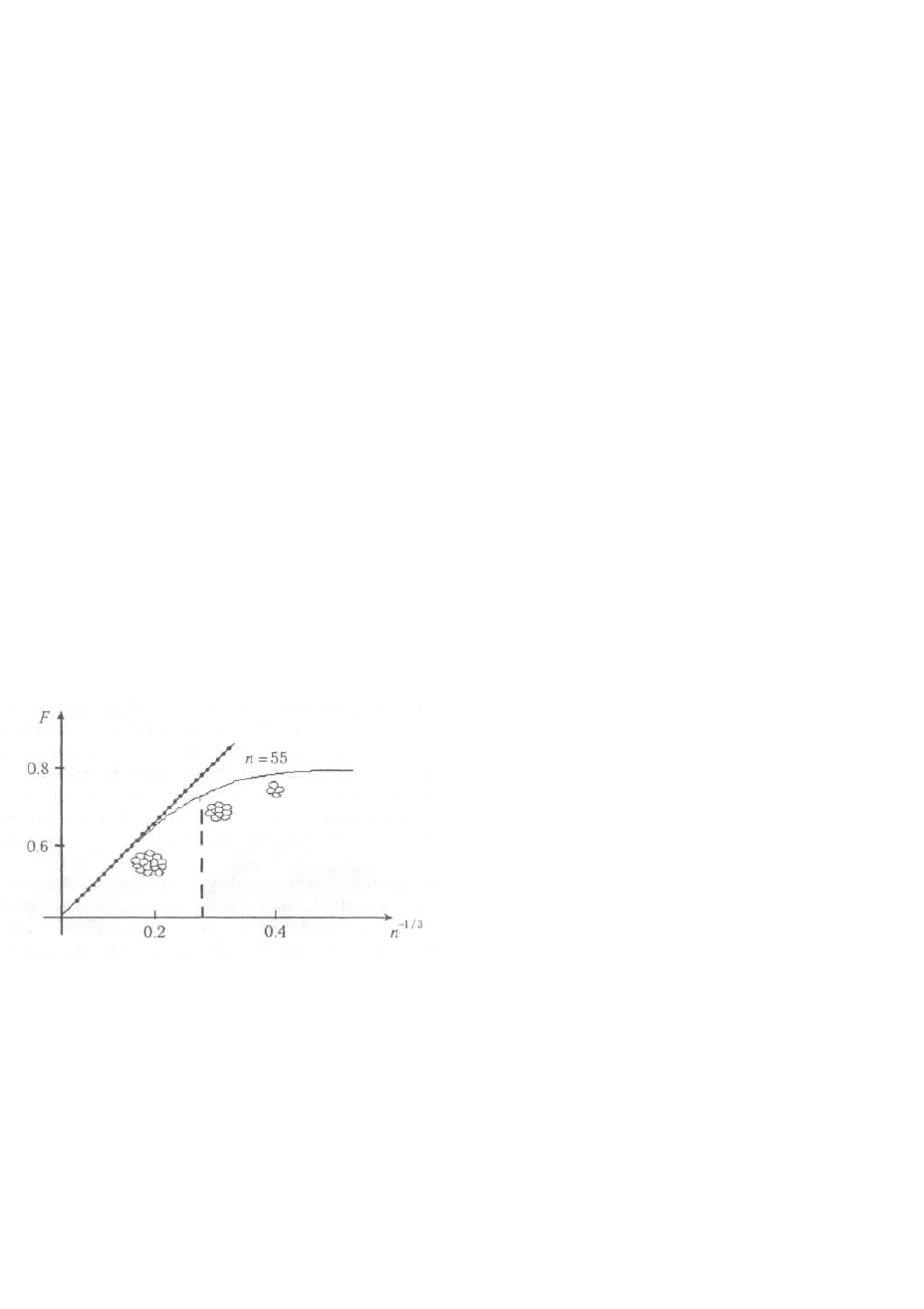
в кластере. Так, например, зависимость F от размеров кластеров благородных

газов с икосаэдрической структурой незначительно отличается от модели жид-

кой капли (рисунок 4).

Рис.4.

Теоретические и имитационные моде-

ли включают моделирование энерге-

тических поверхностей, проведение

молекулярно-динамических расчетов

и квантово-химических расчетов. Экс-

периментальные исследования по-

верхности кластеров также позволяют

получить сведения о ее структуре и

величине F.

Таким образом, в отличие от конденсированной среды в кластерах боль-

шая доля частиц находится на поверхности кластера. Это приводит к появле-

нию у кластеров таких свойств, которые отсутствуют в макроскопических сис-

темах. К числу таких свойств можно отнести появление различных электрон-

ных и колебательных поверхностных возбуждений, включая поверхностные

фононные и экситонные возбуждения и другие элементарные возбуждения.

Само используемое нами понятие поверхности кластера, однако, являет-

ся достаточно условным. Изменение плотности в кластере в действительности

не резкое, а плавное и может быть приближенно описано функцией:

})/)(2{1(

)(

lRrthr





, (7)

где l - толщина поверхностного слоя.

В частности, например, для кластера (H

100

при 300° К молекулярно-

динамические расчеты дают величину l  4 Å. Отметим, что аналогичная фор-

мула для плотности используется и в ядерной физике для ядер, содержащих

большое число нейтронов и протонов. Это является еще одним свидетельством

большой общности самых разных систем, объединенных понятием кластер.

Рассматриваемые здесь кластеры по природе взаимодействия разделяются на

несколько типов (см. таблицу).

Таблица 1

Классификация Примеры

Кластеры, состоящие из атомов

инертных газов

(He)

; (Xe)

; (Ar)

Ван-дер-ваальсовые кластеры (SF

)

; (CO

)

Кластеры с водородными связями (H

; (NH

)

Металлические кластеры (Na)

; (K)

Ионные кластеры (KCl)

; (NaCl)

Первые три типа кластеров, фигурирующие в таблице 1, характе-

ризуются короткодействующим типом взаимодействия. В металлических кла-

стерах взаимодействие имеет конечный радиус действия, а в ионных кластерах

основным является дальнодействующее взаимодействие. В качестве иллюстра-

ции, приведем некоторые примеры.

Кластеры из атомов инертных газов

Кластеры из атомов инертных газов представляют собой простейший и

наиболее изученный тип кластеров. На рисунке 5 приведено изображение кла-

стера, состоящего из 16 атомов аргона.

Рис.5.

Атомы инертных газов с полностью заполненными

электронными оболочками слабо взаимодействуют друг с

другом посредством Ван-дер-ваальсовых сил. Характерная

энергия связи, т.е. энергия, затрачиваемая на отрыв атома от

кластера, очень мала и составляет примерно 10 - 100 К.

При описании таких кластеров с достаточно хорошей точностью при-

менима модель твердых шаров. В настоящее время с помощью описанной вы-

ше технологии газопламенных кластерных пучков удается создавать кластеры

из атомов инертных газов, содержащие от нескольких единиц до десятков ты-

сяч атомов. Кластеры из атомов инертных газов представляют собой уникаль-

ный объект для изучения атом - атомных взаимодействий различных типов

возбуждений в таких кластерах, электрон - атомного взаимодействия и т. д. К

числу важных технических применений кластеров из атомов инертных газов

относятся:

 выравнивание поверхностей, в частности создание идеально ров-

ных поверхностей зеркал (рисунок 6, где а- изображение исходной поверхно-

сти, б- изображение поверхности после бомбардировки кластерами, в- изобра-

жение поверхности после бомбардировки ионами);

 очистка поверхностей - поверхностные примеси удаляются при ее

бомбардировке кластерными ионами;

 поверхностная имплантация и многие другие.

Рис.6 а, б, в.

Металлические кластеры

Кластеры из атомов металлов содержат от нескольких единиц до не-

скольких десятков тысяч атомов. В металлических кластерах из нескольких

атомов может реализоваться как ковалентный, так и металлический тип связи.

а б

Металлические кластеры представляют собой важный пример конечной

Ферми-системы и по своим свойствам во многом аналогичны атомным ядрам.

Металлические кластеры используются в технике в качестве катализаторов не

только благодаря большой эффективной площади реакции, но и их собствен-

ной высокой реакционной способности. С металлическими кластерами, им-

плантированными в матрицу, связывают будущий прогресс в нанотехнологии.

Пустотелые кластеры

Фуллерены - это недавно открытая природная форма углерода, сущест-

вующая наряду с уже хорошо известными - графитом и алмазом. Фуллерены

представляют собой полые внутри кластеры, замкнутая поверхность которых

образована правильными многогранниками из атомов.

Особое место среди фуллеренов занимает кластер из 60 атомов углерода

– C

, который напоминает футбольный мяч, только микроскопический, диа-

метром 7 Å. Его поверхность также образована из 5-угольников и 6-

угольников. Широкое изучение фуллеренов началось после 1990 года, когда

был открыт метод получения фуллеренов в макроскопических количествах из

графита в электродуговом разряде.

Фуллерены имеют широкую область применения, которая включает соз-

дание новых типов смазок и антифрикционных покрытий, новые типы топлива,

алмазоподобных соединений сверхвысокой твердости. С фуллеренами связаны

надежды на создание новых классов сверхпроводников, новых классов соеди-

нений для фармакологии, медицины и др. За открытие фуллеренов в 1996 г. Р.

Керлу, Р. Смолли и Г. Крото была присуждена Нобелевская премия.

Соединения, подобные фуллеренам могут образовываться и из химиче-

ского элемента, относящегося к металлам – золота. В 2005 году была опубли-

кована теоретическая работа, в которой на основе расчетов теории функциона-

ла плотности, показана возможность существования полого сфероидального

кластера из атомов золота. В мае 2006 полые кластеры Au

, где n=1618, были

зарегистрированы экспериментально в газовой фазе методом фотоэлектронной

спектроскопии. Так называемый "bucky gold" имеет диаметр >5.5 Å, следова-

тельно, он, так же как и углеродный фуллерен, может быть эндоэдральным.

Ионные кластеры

На следующем рисунке изображен типичный пример ионного кластера с

химической формулой Na

. Он представляет классическую картинку, тесно

связанную с иллюстрациями, которые приводятся в учебниках для ионной свя-

зи в решетке кристаллов NaCl. Если ионный кластер достаточно велик, его

структура близка к структуре объемного кристалла. Таким образом, изобра-

женный кластер представляет собой пример нанокристалла. Такие ионные на-

нокристаллы могут найти применение в создании фотопленок с высоким раз-

решением, молекулярных фотодетекторов, различных разделах микроэлектро-

ники и электрооптики.

Фрактальные кластеры

Фрактальным называется объект с расползающейся, разреженной струк-

турой. При наблюдении таких объектов с возрастающим увеличением можно

видеть, что они проявляют повторяющуюся на разных уровнях картину. Дру-

гими словами, одна и та же структура наблюдается в любом масштабе.

Для кластера с фрактальной структурой соотношение (1) неверно и заме-

няется на соотношение n = cR

, в котором D выражается дробным числом, иг-

рающим роль фрактальной размерности. Пример фрактального кластера, полу-

ченного путем машинного моделирования, изображен на рисунке. Фракталь-

ной структурой обладают: сажа, коллоиды, а также имеющие широкую область

применения аэрозоли и аэрогели.

Молекулярные кластеры

Собственно подавляющая часть кластеров является молекулярными.

Рис.7.

Их разнообразие и число практически не ог-

раничены. Изучение молекулярных класте-

ров и составляет основной предмет физики

кластеров. Биологические макромолекулы

можно рассматривать как сложные молеку-

лярные кластеры. На рисунке 7 изображен

белок - ферредоксин.

Кластеры с плотной упаковкой и заполненными оболочками

Модель кластеров с плотной упаковкой и короткодействующим взаимо-

действием

Для случая взаимодействия атомов и молекул понятие короткодейст-

вующего взаимодействия понимается так, что в области координат, опреде-

ляющей взаимодействие атомных частиц, расстояние между ними меняется

мало по сравнению с некоторым характерным размером. Короткодействующее

взаимодействие атомных частиц включает в себя как притяжение, так и оттал-

кивание. Максимум потенциала притяжения атомных частиц отвечает конеч-

ному расстоянию между атомами или молекулами. Потенциал взаимодействия

двухатомных частиц удобно аппроксимировать зависимостью типа:

})/()/({)(

RRlRRk

RU 





, (8)

где R - расстояние между атомными частицами; R

- равновесное рас-

стояние между ними, отвечающее минимуму потенциала взаимодействия; D -

максимальная глубина ямы; k, l - параметры. В случае Леннард -Джонса:

})/(2)/{()(

612

RRRRDRU



, (9)

Короткодействующее взаимодействие атомов в области притяжения ха-

рактеризуется узкой и неглубокой ямой в потенциале взаимодействия частиц.

В этом случае в системе большого числа связанных атомов – кластерах - имеет

место только парное взаимодействие между ближайшими соседями, и взаимо-

действие между двумя атомами в такой системе не зависит от взаимодействия

этих атомов с другими соседями. Рассматриваемую систему удобно описывать

моделями, в которых атомы заменены шарами. Если эти шары являются жест-

кими, т.е. расстояние между ближайшими соседями строго фиксировано, то

образуемая структура носит название структуры с плотной упаковкой. Эта

структура реализуется в кристаллах с кубической гранецентрированной и гек-

сагональной решеткой. Однако возможна и такая структура, когда расстояния

между ближайшими соседями находятся в некотором интервале и моделиру-

ются “мягкими” шарами. Важнейшей структурой кластера, который моделиру-

ется атомами в виде мягких шаров, является икосаэдр. Это распространенная

структура кластеров, которую группы атомов часто образуют в металлах, спла-

вах и других конденсированных системах.

Итак, в связи с модельным характером проводимого анализа мы пренеб-

регаем дальнодействующим взаимодействием. Далее нас будет интересовать

только область притяжения, которая определяет свойства конденсированной

системы рассматриваемых атомов. Аппроксимируем потенциал взаимодейст-

вия выражением вида:

,))((

.,,0

{)(

RRRRRRUD

RRRR











, (10)

где U

”

- вторая производная от реального потенциала взаимодействия в

минимуме потенциала.

Более удобной является следующая форма потенциала взаимодействия:

)2/)(exp()(

rRRDRU



, где

2/1

))(/(

RUDr





, (11)

Благодаря использованию этого приближения, были получены следу-

ющие результаты. Оказывается, что эта модель лучше описывает вза-

имодействие в системах, связанных атомов инертных газов, чем модель лен-

нард-джонсовского взаимодействия. Это становится ясным при сравнении раз-

личных параметров, подсчитанных в результате моделирования и полученных

экспериментально. Вот три из них:



sub

= 8,61D, α = R

- для Леннард-Джонса;



sub

= 6,0D, α = R

- для модели (11);



sub

= 6,6D, α = R

- для атомов аргона (экспериментально),

где 

sub

- энергия сублимации кристалла при нулевой температуре, при-

ходящейся на один атом, α - расстояние между ближайшими соседями в кри-

сталле инертного газа при нулевой температуре. Степень совпадения парамет-

ров характеризует степень применимости моделей.

Анализ характеристик некоторых кластеров с плотной упаковкой и за-

полненными оболочками

Кластер с плотной упаковкой обладает высокой симметрией, которая

может быть использована при построении кластера. Такая симметрия сохраня-

ется и в различных геометрических фигурах - октаэдрах, декаэдрах и т.д., кото-

рые образуют атомы кластера. Анализ кластеров с плотной упаковкой симмет-

ричной формы дает информацию об энергетических параметрах таких класте-

ров. Был разработан простой метод анализа кластеров со структурой кубиче-

ской гранецентрированной решетки и короткодействующим взаимодействием

атомов, позволяющий определять энергетические параметры кластеров, со-

держащих сотни атомов, которые занимают в кластере произвольную конфи-

гурацию. Использование этого метода позволяет с единых позиций проанали-

зировать различные замкнутые структуры с плотной упаковкой. Поскольку

взаимодействие атомов инертных газов носит короткодействующий характер,

полученные результаты могут быть использованы для кластеров, состоящих из

атомов инертных газов, а также для конденсированных инертных газов.

Анализ симметричных структур кластеров допускает обобщения, позво-

ляет рассмотреть замкнутые структуры с мягкой упаковкой, примером которых

является кластер икосаэдр. На рисунке показаны два первых кластера из этой

серии, содержащие соответственно 13 и 55 атомов.

В 13-атомном кластере все атомы, за исключением одного, занимают эк-

вивалентные позиции; 55-атомный кластер из этой серии содержит ядро, яв-

ляющееся 13-атомным икосаэдром, к каждой из вершин которого добавлено по

атому, плюс 30 атомов по одному атому в центре каждого из 30 ребер икосаэд-

ра. Не показанный на рисунке 147-атомный кластер включает в качестве ядра

55-атомный икосаэдр, к которому добавляется 12 атомов - по одному атому к

вершинам самой удаленной от центра кластера оболочки, еще 20 атомов по од-

ному атому в центре каждой из 20 граней и 60 атомов по два атома вдоль каж-

дого из 30 ребер кластера.

Итак, в силу симметрии кластера процедура построения кластера связана

с разделением его на оболочки, так что координаты всех атомов данной обо-

лочки могут быть получены из координат одного из них в результате преобра-

зований:

1. X  Y  Z

2. X  -X, Y  -Y Z  -Z. (12)

Это позволяет далее ограничиться рассмотрением положения только од-

ного из атомов оболочки.

Поскольку расстояния между соседними атомами строго фиксированы,

энергия связи двух ближайших соседей равна D. Поэтому энергия связи всех

атомов в кластере составляет:

kDE



, (13)

где k - число связей между ближайшими соседями. Далее будем вы-

ражать энергию в единицах D.

При большом числе атомов в кластере n большинство из атомов нахо-

дятся внутри кластера и имеют 12 ближайших соседей. Поэтому имеется асим-

птотическая зависимость E

 6 при n  . Удобно ввести поверхностную

энергию:

EnE

sur





}{

, (14)

Очевидно, оптимальной структуре кластера соответствует минимальная

поверхностная энергия. Это определяет характер сборки кластера при добавле-

нии к нему нового атома. Проведенный анализ дал следующие результаты.

Малые кластеры могут расти в результате заполнения отдельных оболочек, од-

нако, как правило, имеет место одновременное заполнение нескольких оболо-

чек. Тем самым рост кластера при добавлении к нему новых атомов связан с