Черненко В.Д. Высшая математика в примерах и задачах (том 1)
Подождите немного. Документ загружается.


190 Гпава 4
Используя условие параллельности прямой
и
плоскости (2),
имеем
2(8
+
ЗЯ)
+ 3(2 + 4Я)~2(3 +
Я)
= 0, откудаЯ =
-1.
Под-
ставляя найденное значение Я в уравнение пучка плоскостей,
получим искомое уравнение 5х - 2
j^
+ 2z +
5
= О.
4.8. Найти проекцию прямой
Jjc~33^-z
+ 4
= 0,
l2r-4 +3 -2 = 0 на плоскость
3JC
+
2;;
+ z -
7
= 0.
Решение. Искомая проекция определится, как пересечение
плоскости, проходящей через данную прямую и перпендикуляр-
ной данной плоскости. Составим уравнение пучка плоскостей,
проходящих через данную прямую
x~ЗJ^-z4-4 + Я(2JC-4J;^-Зz-2) = 0
или
(l + 2Я)x-(3 + 4Я)J^-(l-ЗЯ)z + 4-2Я = 0.
Искомая плоскость должна быть перпендикулярна данной
плоскости. Используя условие перпендикулярности двух плоско-
стей для определения неизвестной величины Я, получим уравне-
ние 3(И-2Я)-2(3 + 4Я)-(1-ЗЯ) = 0, откуда
Я
= 4- Подставляя
найденное значение Я в уравнение пучка, находим уравнение
плоскости, проходящей
через
заданную прямую перпендикулярно
к данной плоскости 9х
-19j^
+1
Iz -
4
= О.
Проекция данной прямой на данную плоскость определяет-
ся пересечением плоскостей
r9jc-19j;-Mlz-4 = 0,
[Зх+ 1у + z-7 = 0.
4.9. Найти расстояние от точки М(1,2,~1) до прямой
jc-3_j;-2_z-4
"Т~~
1 "Т"*
Решение. Найдем точку пересечения плоскости, проходящей
через заданную точку перпендикулярно данной прямой. Иско-

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 191^
мое расстояние будет равно расстоянию от точки М до точки
пересечения плоскости и прямой.
Уравнение плоскости, проходящей через точку М, имеет вид
А{х -1) + В{у -
2)
+ C{z +1) =
О.
Из условию перпендикулярности
ABC
прямой
и
плоскости
Т"
~ Т ~
"Т'
полагая множитель пропорцио-
нальности равным единице, находим
^4
=
1,
5 =
1,
С = 2. Следо-
вательно, уравнение искомой плоскости имеет вид
x + jH-2z-l = 0.
Для нахождения точки пересечения плоскости
и
данной пря-
мой решаем совместно уравнения плоскости и прямой. Запишем
уравнение прямой в параметрическом виде:
jc
= / +
3,
j;
=
^
+ 2,
z = 2/ + 4
•
Подставляя эти выражения в левую часть уравнения
данной плоскости / +
3
+ / +
2
+ 2(2/ + 4) -1 =
О,
находим, что па-
раметр
г
равен / =
—2.
Следовательно, координаты искомой точ-
ки суть ^0 =
1,
>'о =
О,
ZQ
= О.
Искомое расстояние от точки М до прямой определяем по
формуле расстояния между двумя точками
J = ^(1-1)4(2-0)4 (-1-0)' =л/5.
4.5. Поверхности второго порядка
Степень алгебраического уравнения, определяющего дан-
ную поверхность, называется порядком этой поверхности.
1°.
Эллипсоид,
Каноническое уравнение эллипсоида имеет вид
а о с
где
а,Ъ,с
— полуоси трехосного эллипсоида (рис. 4.4).
Эллипсоид, две оси которого равны между собой, например
а-Ь^
называется эллипсоидом вращения
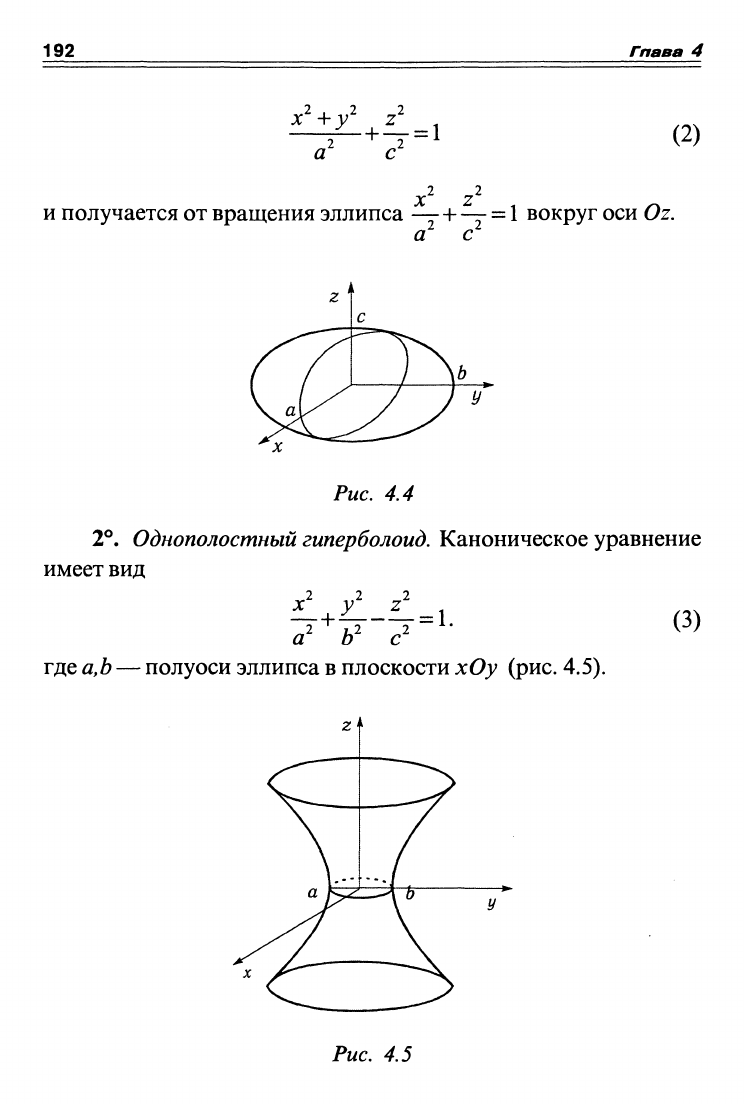
192 Гпава 4
a с
(2)
И
получается от вращения эллипса
—-+-—
=
1
вокруг оси Oz.
Рис. 4.4
2°.
Однополостный
гиперболоид.
Каноническое уравнение
имеет вид
2 2 2
а' ь' г
(3)
где
а,Ъ
— полуоси эллипса в плоскости хОу (рис. 4.5).
Рис. 4.5

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 193
Форму поверхности определяют методом
сечений.
При z=0
^' у' ,
в ПЛОСКОСТИ хОу получают-у +-у =
1
— наименьший из всех
а о
возможных эллипсов, который называется горловым. Сечения
поверхности с плоскостями yOz и xOz образуют гиперболы
2 2 2 2
ос ас
Сечение поверхности с плоскостью х-а образует две пря-
у z у ^
мые —h
—
= 0; = 0. Можно установить, что через любую
be be
точку однопостного гиперболоида проходят две прямые, лежа-
щие на этом гиперболоиде.
Поэтому однополостный гиперболоид называют линейча-
той поверхностью.
Если а = 6, то уравнение (3) принимает вид
а е
и поверхность, соответствующая этому уравнению, называется
однополостным гиперболоидом вращения. Она образуется вра-
щением гиперболы вокруг
ее
мнимой оси.
3°.
Двухполоетный гиперболоид. Каноническое уравнение
имеет вид
а' Ь' г (5)
При
X
=
Л
получаем
ТОЧКИ
^Да,0,0) и
А^{^а,^^^^
—вер-
шины поверхности
(рис.
4.6).
В
сечении
с
плоскостями |х| > а по-
верхность образует
эллипсы.
В
сечении
с
плоскостями хОу
и
xOz
2 2 2 2
получаются гиперболы -^-тт"^' "~Г—Г~^- Поверхность
а b ас
(5) симметрична относительно плоскости ^'Oz.

194
Гпава 4
Рис, 4,6
При Ь- с уравнение (5) принимает вид -^-——^— =
1
и
а b
поверхность, соответствующая этому уравнению, называется
двухполостным гиперболоидом вращения. Она образуется при
вращении гиперболы вокруг оси Ох,
4°.
Эллиптический параболоид. Каноническое уравнение
имеет вид
-—+j^
=
z; р>0; д>0,
2р 2д
(6)
При пересечении
с
плоскостями z
=
h поверхность (6) обра-
зует эллипс
(рис.
4.7).
Рис. 4.7

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
195
В сечении с плоскостями xOzuyOz поверхность образует
параболы х^ = Ipz vi у^
=.
Iqz. При/? = q уравнение (6) прини-
мает вид х^ +у^
=
2pz и поверхность, соответствующая этому
уравнению, называется параболоидом
вращения.
Она образует-
ся вращением параболы вокруг оси z.
5°.
Гиперболический
параболоид.
Каноническое уравнение
имеет вид
2 1
X у
2р 2q
Сечение поверхности (7) с плоскостью хОу образует пару
= z; р>0; q>0.
(7)
прямых J^--^ I "~^i
у - J~^ (рис. 4.8). Сечения поверхности с
плоскостями
Z
=
А
(/| > 0)—гиперболы,
у
которых действитель-
ная ось параллельна оси Ох. Сечения
с
плоскостями
z
=
А
(А < 0)
— гиперболы, у которых действительная ось параллельна оси
Оу. Сечения поверхности
с
плоскостями xOz
и
yOz представля-
ют параболы х^ = 2pz и у^
=
-2qz.
Ху
Рис. 4.8
Если/7 = q, то уравнение (7) принимает вид х^
-k-y^
=
2pz,
гиперболы в сечениях будут равносторонними, а параболы бу-

196 Гпава 4
дут иметь равные параметры.
При повороте системы координат вокруг оси Oz на угол
135°
уравнение
(7)
примет
вид
ху = pz. Сечения поверхности плос-
костями
Z
=
Л
суть равносторонние гиперболы. Плоскость хОу
пересекает эту поверхность по осям координат.
6°.
Цилиндрические поверхности. Уравнения, не содер-
жащие какой-либо одной координаты, в пространстве изоб-
ражаются цилиндрическими поверхностями, образующие
которых параллельны отсутствующей координатной оси. Само
же уравнение есть уравнение направляющей кривой этого
цилиндра.
1.
Эллиптический цилиндр (рис. 4.9)
2 2
(8)
Направляющей, лежащей в плоскости хОу, служит эллипс.
Если а=Ь,то направляющая есть круг, а цилиндр называется
круговым.
Рис. 4,9
2.
Гиперболический цилиндр (рис. 4.10)
2 2
Направляющей является гипербола.
(9)

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
197
Рис, 4.10
3.
Параболический цилиндр (рис. 4.11)
у^
= 2рх,
(10)
Рис. 4.11
Направляющей является парабола.
Аналогично записываются уравнения цилиндрических по-
верхностей с образующими, параллельными координатным
осям OxwOy,
7°.
Поверхность, образованная движением прямой, прохо-
дящей через неподвижную точку пространства
и
пересекающей
при этом некоторую кривую, называется конической поверх-
ностью.

198
Гпава 4
Неподвижная точка называется вершиной, кривая — на-
правляющей
и прямая —
образующей
конической поверхности.
Каноническое уравнение конуса, когда ось симметрии конуса
совпадает с осью Oz (рис. 4.12), имеет вид
2 2 2
а' b' г
(11)
Рис. 4.12
Если а
=
ЬФс — конус круговой; если а
= Ь =
с,
тох^
+у^ -z^ =0 — прямой круговой
конус,
образующие накло-
нены к плоскости хОу под углом 45°.
5.1.
По заданному уравнениюf(x,y,z) =
О
определить вид по-
верхности и указать ее расположение в координатной системе:
а) x^
+
y^+z^-2x
+
4y-6z
+ 5 =
0;
б) 4x44/+ 5z'-20 = 0;
в) 5x'+5/-4z'-20 =
0;
г) 4x'+/-2z =
0;
д) x^+z^-y
=
0;
ж) /-4z-5 =
0;
з) /-8x+3 = 0.
Решение, а) Дополним до полных квадратов многочлен в
левой части х^-2х
+ 1 +
у^ +4y
+
4+z^-6z
+
9-9
=
0 или
(x-lf+(y
+
2fHz-3y-=3\
Полагая
jc'
= jc~l;
j;'
=
j;
+ l; z' = z-3, находим, что в сис-
теме координат
л:',
у\ z\ смещенной относительно системы х,
у,
Z параллельным переносом в точку с координатами
JCQ
=
1;
jVo
=
-1;
ZQ
= 3
,
данная поверхность имеет простейшее

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 199
уравнение вида jc'^H->'*^+z'^ =3^. Таким образом, данное
уравнение определяет сферу с центром в точке
0*(1,-2,3)
и
радиусом равным i? = 3.
б) Перенесем свободный член в правую часть и разделим
на него, тогда будем иметь
2 2 2
X у Z ^
5 5 4
Данное уравнение представляет эллипсоид вращения вок-
руг оси
Z
с полуосями а
= Ь =
yfS;
с = 2.
в) Пернесем свободный член в правую часть и разделим на
2 2 2
него,
тогда будем
иметь
н =
1.
^ 4 4 5
Данное уравнение представляет однопол остный гиперболоид
вращения (4) вокруг оси z.
г) Разрешим выражение относительно z, тогда будем иметь
2 2
X у
1
2
2
Данное уравнение представляет эллиптический параболо-
ид (5).
д) Разрешим выражение относительно у, тогда получим
y
=
x^+z^' Нетрудно заметить, что это уравнение предствляет
параболоид вращения с осью вращения у
(рис.
4.13).
Рис. 4.13
