Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

200

Гпава 4

ж) Поскольку переменная х отсутствует, то уравнение

z^—y'^

— представляет параболический цилиндр с образую-

4 4

щими параллельными оси х

(рис.

4.14). Сечение параболическо-

го цилиндра с плоскостью Oyz образует параболу, вершина

которой находится

точке

координатой z = ---.

Рис. 4.14

з) Поскольку переменная z отсутствет, то выражение

_1 2 3

^ - — J^ +

т-

представляет параболический цилиндр, образую-

о о

щие которого параллельны оси z

(рис.

4.15). Сечение параболи-

ческого цилиндра с плоскостью Оху образуют параболу, вершина

которой находится в точке

координатой х

—.

^ I

Рис. 4.15

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 201[

5.2.

Установить поверхность, определяемую уравнением:

а)

4JC'+V+16Z'-16JC

36J;

32Z

= 0;

б) jc'-4/+4z42x + 8;;-7

= 0;

в)

JC'-16/-4Z'-10JC-64;;

24Z-48

= 0;

г) 5x42;; + 3z'-9 = 0.

Решение, а) Поскольку уравнение не содержит произведе-

ний координат, то приведение его

простейшему виду осуще-

ствляется посредством параллельного

переноса.

Вьщелим полные

квадраты

Ах" +9/ +16z' -16x +

36;;

+ 32z +

= 4(x'~4x-f4) + 9(/+4>^ +

+ 16(z42z + l)"-9 =

= 4(jc-2)'+9(>^ + 2)'+16(z +

l)'-9.

Полагая

= x-2,

у'-уЛ-2,

= z + l, находим, что в си-

стеме координат

х\ у\ z\

смещенной относительно системы

x,y,z

паралельным переносом начала в точку с координатами

= 2,

= -2, с = -1 данная поверхность имеет простейшее

уравнение вида

(jc')

(У) (zjc)

4(jcf+9(>^')4l6(zy=9 или

/з/\'"^

"^fVf

"^'

Таким образом, данное уравнение определяет эллипсоид

(1)

центром

точке 0'(2,~2,-1)

полуосями

3/2,

= l, с =

3/4.

б) Уравнение

не

содержит произведений координат. Преоб-

разуем левую часть до полных квадратов

X42JC

1-4(/-2>;

1)H-4Z'-4

1)'-4(:H-1)'-H4Z'-4.

Полагая

JC*

y' = jv-l,z* = z, получим уравнение по-

верхности

системе координат x'j^'z' смещенной относительно

202 Гпава 4

системы x,y,z параллельным переносом начала в точку

O'(-l,l,0)

(х')^-4(;;')Ч4(2')^=:4или^^-(3^^+(zf =1.

Поскольку

этом уравнении коэффициенты при {x'f и (z')^

положительные, а при {у

')^

— отрицательный, то данное урав-

нение определяет однополостный гиперболоид

(3),

расположен-

ный вдоль оси

j^'.

в) Преобразуя левую часть до полных квадратов, прихо-

дим к уравнению (^ -

5)^

~ 1

Ь{у

+ Tf - 4(z -

3)^

О,

из которого

после замены

jc*

= x-5,

у'-уЛ-1,

z'-z-Ъ получим уравнение

поверхности в системе координатх\у \z\ смещенной относитель-

но системы x,y,z параллельным переносом начала координат в

точку (5,-2,3)

(jcf-16(>^')'-4(zf=0.

Поскольку в этом уравнении свободный член равен нулю и

коэффициенты при квадратах координат разных знаков, то дан-

ное

уравнение определяет

конус

второго порядка

(11) с осью

вдоль

оси X' и вершиной в точке

(5,

-2,3).

г) Данное уравнение содержит две координаты во второй

степении одну в первой, следовательно, уравнение определяет

эллиптический парболоид (5). Переписывая его в виде

5х^ +3z^ =-2(j;-9/2), заключаем, что вершина параболоида

расположена в точке

координатами

О'(0,9/2,0)

и его полость

обращена в сторону отрицательных значений ;;. Если обозна-

чить

JC'

у'•=^

у-912,

Z *

то получим каноническое урав-

нение параболоида (рис. 4.16)

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

203

Рис, 4.16

4.6.

Геометрический смысл уравнений

с тремя неизвестными в пространстве

1°.

Рассмотрим уравнение с тремя неизвестными

F{x,y^z) = 0.

Предположим, что уравнение может быть разрешено от-

носительно

то есть

= /

(л:,

у). Данное уравнение в простран-

стве представляет поверхность и называется уравнением

поверхности.

Если поверхность определена геометрически, т. е. задано

некоторое свойство, принадлежащее всем ее точкам и не при-

надлежащее другим точкам пространства, то можно составить

уравнение этой поверхности. Заданное геометрическое свойство,

выраженное уравнением, связывающим текущие координаты, и

будет уравнением поверхности.

2°.

Всякую линию в пространстве можно расматривать как

пересечение двух поверхностей F{x,y, z) =

(х,

JH,

^) =

О.

То

есть,

линия в простванстве рассматривается как геометричес-

кое место точек, координаты которых удовлетворяют системе

этих уравнений.

6.1.

Найти геометрическое место точек, равноудаленных от

двух данных точек М(2,1,-1) и Л^(~3,0,3).

204 Гпава 4

Решение. Пусть точка P(x,y,z) будет текущей точкой иско-

мого геометрического места

точек.

Тогда, по формуле

(11,

Гл.2.2)

данное условие примет вид

V(x-2)Ч(;;-l)Ч(z + l)^=V(^-^3)Ч(J-0)Ч(z-3)^

Упрощая, получим уравнение геометрического места то-

чек 5x

y-4z

+ 6 =

0, Полученное уравнение изображает плос-

кость, перпендиклярную отрезку MN и пересекающую его

посередине.

6.2. Найти геометрическое место точек, удаленных на рас-

стояние

единиц от точки

С(1,

-2,1).

Решение. Пусть точка M{x,y,z) есть текущая точка поверх-

ности. Тогда, воспользовавшись формулой (11,Гл.2.2), по усло-

вию задачи будем иметь (х -1)^ +

(j^

2)^

+ (^""

1)^

25.

Данное

уравнение представляет сферическую поверхность с центром в

точке С и радиусом R = 5.

6.3.

Каков геометрический смысл системы уравнений

Решение. Первое уравнение есть сфера, второе представля-

ет в пространстве плоскость. Подставляя z =

в первое уравне-

ние,

получим

x^+j;^

=16. То есть пересечение плоскости со

сферой есть окружность, параллельная плоскости Оху, с цент-

ром в точке С(0,0,3) и радиусом равным 4.

6.4. Найти проекцию линии пересечения конуса

x^+y^-3z^ =0 (z > 0) и сферы (х -if л-у^+z^ =\ на коорди-

натную плоскость Оху.

Решение. Находим уравнение проектирующего цилиндра.

Для этого исключаем из уравнений поверхностей переменную z.

Умножая второе уравнение на 3 и складывая с первым, полу-

чим

4JC^

6Х

4у^ =

О.

Таким образом, проекция линии на плос-

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

205

кость Оху определяется следующей системой: х^ л-у^ —х = 0;

2 =

Выделяя в первом уравнении полный квадрат, получим

X— +>'^ =—• Следовательно, проекция линии пересечения

поверхностей на плоскость Оху представляет окружность

цен-

тром в точке О,

(

4^ ;01 и радиусом, равным -j.

6.5.

Тело в пространстве задано системой неравенств. Оп-

ределить вид поверхностей, ограничивающих это

тело.

Указать

по каким линиям и в каких плоскостях пересекаются эти повер-

хности: а) x^+y<(z~2)S

x"+y<z

б) x^+3;^+z" <25,

хЧ/<9;в) x'+/-9>z',

ХЧ/<16.

Решение, а) Уравнение х^ +у^ ={2- if задает в простран-

стве конус, смещенный вверх по оси Oz на 2. Неравенство

х^

+у^ <{z- Tf показывает, что поверхность ограничивает тело

внутри конуса.

Уравнение х^

л-у'^

-z задает в пространстве параболоид, а

неравенство х^

Л-у'^

<z показывает, что поверхность ограничи-

вает тело внутри параболоида. Объединяя результаты, мы полу-

чим, что тело, ограниченное заданными поверхностями, имеет

вид (рис. 4.17).

Рис. 4,17

Решая совместно уравнения поверхностей х^ +у^ =z и

х^

-{-у^

={z- if, находим, что z = 1, то есть поверхности пере-

206

Гпава 4

секаются по окружности х^ +

j;^

в плоскости z = 1.

б)

Уравнение х^ +

j;^

= 25 задает сферу с центром

нача-

ле

координат

радиусом равным

Неравенство х^ +

>?^

< 25

показывает, что ограничивает

тело

внутри сферы.

Уравнение х^+>'^=9 задает цилиндрическую поверх-

ность с осью Oz и радиусом 3. Неравенство х^ л-у^ <9 пока-

зывает, что ограничивает тело внутри цилиндра. Таким

образом, тело, ограниченное заданными поверхностями, име-

ет вид (рис. 4.18).

Очивидно,

что

линиями пересечения поверхностей будут ок-

ружности того же радиуса, что и направляющая цилиндра. Те-

перь определим, в каких плоскостях пересекаются поверхности.

Для этого из системы уравнений исключим x\iy. Подставляя

jt^

л-у^

уравнение сферы, получим z^ = 16, z = ±4. Следова-

тельно, поверхности пересекаются по окружности в плоскостях

z = ±4.

Рис, 4,18

в) Уравнение

j^-\-^-^

задет в пространстве однополост-

ный гиперболоид

осью вращения

Oz и

радиусом окружности в

плоскости Оху равным 3. Неравенство х^ +

j;^

-9 > z^ показы-

вает, что тело находится вне поверхности.

Уравнение х^ +у^=

задает цилиндрическую поверхность

радиуса 4 с осью Oz. Неравенство х^ +

j;^

показывает, что

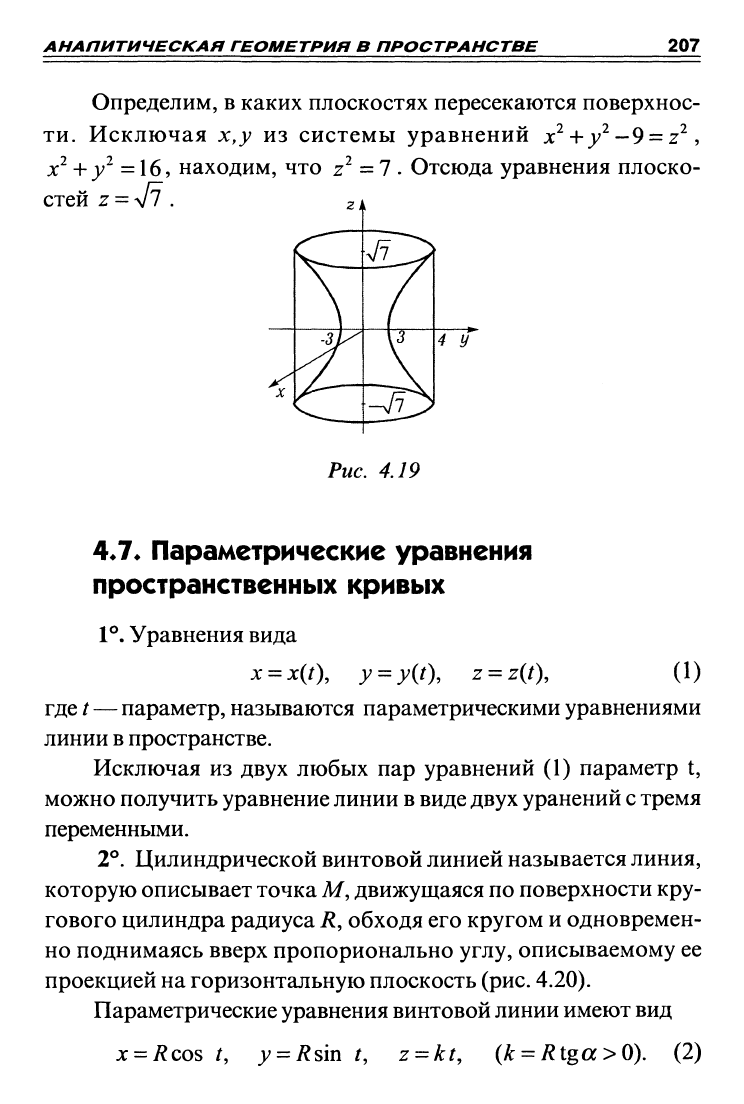
тело находится внутри цилиндра. Таким образом, тело находит-

ся

между однополостным гиперболоидом

цилиндром

(рис.

4.19).

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

207

Определим, в каких плоскостях пересекаются поверхнос-

ти.

Исключая х,у из системы уравнений

х^+з;^--9

= 2^,

х^ +

j;^

= 16, находим, что z^ =1

Отсюда уравнения плоско-

стей

= yjl .

Рис. 4.19

4Л.

Параметрические уравнения

пространственных кривых

1^.

Уравнения вида

x = x{t\ y = y{t\ z = zitl (1)

где

— параметр, называются параметрическими уравнениями

линии в пространстве.

Исключая из двух любых пар уравнений (1) параметр t,

можно получить уравнение линии в виде двух уранении с тремя

переменными.

2^.

Цилиндрической винтовой линией называется линия,

которую описывает точка М, движущаяся по поверхности кру-

гового цилиндра радиуса R, обходя его кругом и одновремен-

но поднимаясь вверх пропорионально углу, описываемому ее

проекцией на горизонтальную плоскость

(рис.

4.20).

Параметрические уравнения винтовой линии имеют вид

= 7?cos /, y = Rsin t, z = kt, (k = Rtga>0). (2)

208

Гпава 4

Если

/с

О,

то уравнения (2) называют уравнениями правой

винтовой линии, если же

/с

эти уравнения представляют ле-

вую винтовую линию.

Когда точка М совершит полный оборот, апликата

точки

Л/увеличится на величину, называемую шагом или ходом вин-

товой

линии,

равным / = InR tg а.

Рис. 4.20,

7.1.

Определить линию, заданную уравнениями

= (/ -1)^,

= 3(^4-1) и z = -(/ + 2).

Решение. Исключая из второго и третьего уравнения па-

раметр t, получим

3zH-3

= 0 —уравнение плоскости. На-

ходя из второго t и подставляя в первое уравнение, будем иметь

9JC

= {y-iy — параболический цилиндр. Следовательно, мы

имеем линию пересечения плоскости с параболическим цилин-

дром.

7.2.

Определить

линию,

заданную уравнениями: х =

cos t

= 4cos/, z = 5sinr.

Решение. Деля первое уравнение на второе, получим

4х -

3j;

— уравнение плоскости.

Возводя

квадрат левые

правые части каждого

из трех

урав-

нений

складывая, получим

х^

j^^

+z^ =

—уравнение сферы.

Следовательно, мы имеем линию пересечения плоскости

со

сферой.

Глава 5

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ ЛЛГЕБРЫ

5.1.

Линейные преобразования

Линейное преобразование двух переменных

а^^х+а^^у\

а^,х+а^^у

выражает значения переменных х и у через значения пермен-

яыхх'и у'.

Равенство (1) можно рассматривать как линейное преобра-

зование координат точки (или вектора) на плоскости. Линейное

преобразование (1) характеризуется его матрицей

(1)

А =

V^«21 '^22 J

Линейное преобразование трех переменных

a^^x+a22y'+a2jz', (2)

выражает значения переменных x,y,z через значения переменных

х',у'Х