Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

150 Гпава 3

точка М имеет координаты М(х;—) и принадлежит параболе

(рис.

3.40), тогда х - р— или х^-р. Отсюда длина половины

искомой хорды равна/7, следовательно, длина всей хорды MN

равна 2р.

Рис, 3.40

6.17. Определить координаты вершины параболы, величи-

ну параметра

уравнение оси симметрии, если парабола задана

уравнением }P--^x-Ay-^\2-Q.

Решение.

Дополним

левую

часть уравнения до полного квад-

рата переменной у

/-4j+4^8x+12-4 = 0 или {y-2f

4(х-1).

Следовательно, вершина параболы имеет координаты х^- 1,

у^-

2. Параметр

= 4, а ось симметрии параллельна оси Ох и

имеет уравнение J = 2.

6.18.

Найти

уравнение параболы, симметричной относитель-

но оси ординат, если известно, что парабола проходит через точ-

ки М(-3;6) и 7V(2;-4).

Решение. Искомое уравнение параболы примем в виде

у-ах^-^с.

Подставляя координаты точек, будем иметь 6= 9а+с, -

4 =

Аа+с.

Решая эту систему, находим, что а =2, с =-12. Следова-

тельно, условиям задачи удовлетворяет парабола j =2x^-12.

6.19. Найти

уравнение параболы, симметричной относитель-

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ

151

НО

оси ординат, если известно, что парабола проходит через точ-

ки (1;2), (2;4) и (3;8).

Решение. Подставляя координаты точек в общее уравнение

параболы, получим систему

а-\-

Ь +

с = 2,

\4а

+ 2Ь +

с = 4,

\9а

+ ЗЬ-\-с

= 8.

Из решения системы находим, что a=l,b=-l,c -2. Таким

образом, условиям задачи удовлетворяет парабола^ =х^-х+2.

6.20. Найти координаты вершины, написать уравнение оси

симметрии и построить параболу, заданную уравнением

у = 5+4х-х^.

Решение. Преобразуем правую часть уравнения, вьщелив в

ней полный квадрат у = 5-(х^-4х+4)+4=9-(х-2)^. Вершина пара-

болы находится в точке, которая имеет наибольшую ординату,

т. е. в точке х

=2,

у = 9. Отсюда уравнение оси симметрии х = 3.

Перенос начала координат в вершину при параллельном

перемещении осей по формулам х =х'-^2иу =у

'+9

дает

у'

^^(х

)^.

Знак минус указывает, что ветви параболы направлены вниз.

Помещая в системе хОу новую систему л:'О';;'с началом в точке

0'(2;9), строим параболу

j^'

= -(х)^ (рис. 3.41).

' и

У=

Нх-2Г\

Рис. 3.41

152

Гпава 3

6.21.

Построить параболу по заданному уравнению

у2_

^у _ бх+ 4= 0.

Решение. Первые два члена дополняем до полного квадрата,

а остальные члены переносим в правую часть У-8;;+16=6х-4+16

или (y-4)^=6(x+2). Отсюда видно, что вершина параболы имеет

координаты

(-2;4)

ось симметрии определяется уравнением ;М= 0.

Переходя по формулам у -у

'+4,

х =х -2 к новой системе ко-

ординат

х'О'j^'с

началом 0'(-2;4), находим, что (у')^=6х'. Таким

образом, парабола имеет вид

(рис.

3.42).

0\-2;4)

Рис. 3.42

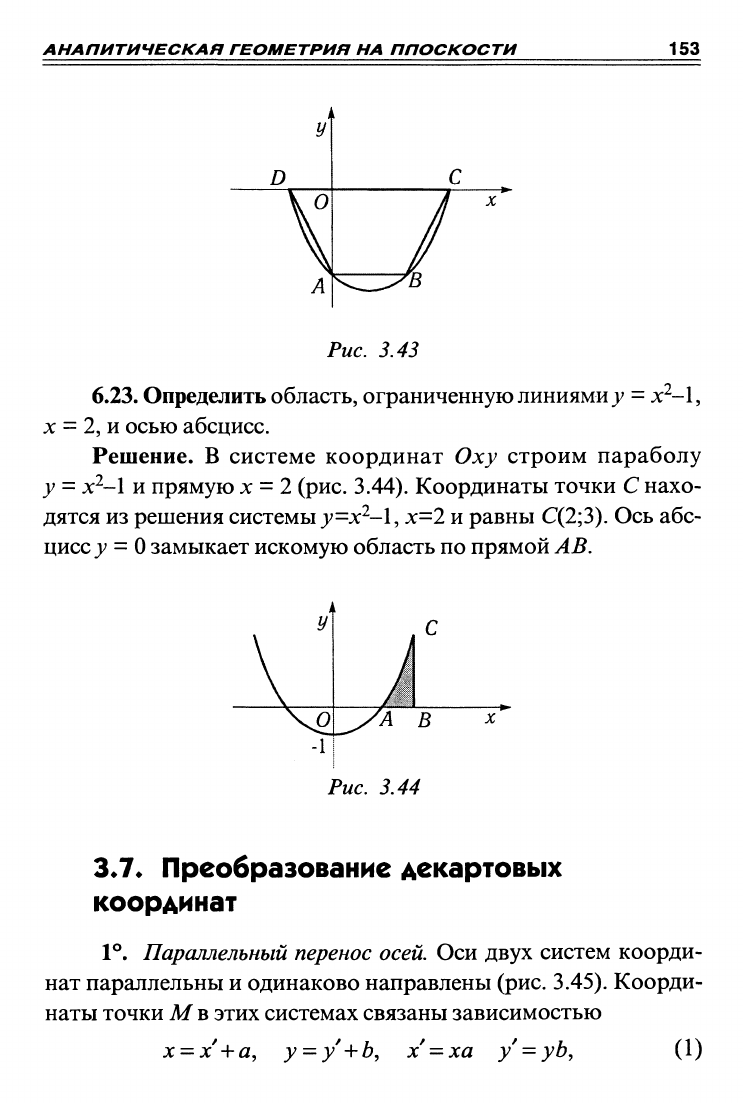
6.22. Определить площадь трапеции, вписанной в параболу

у =х^-4х-\2, если одно из оснований трапеции лежит на оси Ох,

а второе основание проходит через точку пересечения параболы

с осью Оу.

Решение. Полагая х =

О,

находим точку пересечения пара-

болы с осью Оу, то есть ^4(0;-!2) (рис. 3.43). Высота трапеции

АО

12.

Длины оснований определим по абсциссам точек пере-

сечения параболы с прямыми у -Оиу

-\2.

Абсциссы концов основания DC находим из уравнения

х^-Ах-12=

О,

откуда Xj

=-2,

^2=

а концов основания АВ

из

урав-

нения

х^-4х=

О,

откуда

х^=

О,

^2= 4. Таким образом, верхнее ос-

нование DC= 8, а нижнее АВ= 4. Площадь трапеции равна

= 12 = 72 кв.ед.

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ

153

"^-„-И^

Рис, 3.43

6.23. Определить область, ограниченную линиями;; =

х^-1,

= 2, и осью абсцисс.

Решение. В системе координат Оху строим параболу

х^-1 и прямую

= 2 (рис. 3.44). Координаты точки С нахо-

дятся из решения системы

j;=x^-l,

х=2 и равны С(2;3). Ось абс-

цисс

замыкает искомую область по прямой АВ.

Рис. 3.44

ЗЛ.

Преобразование декартовых

координат

1°.

Параллельный перенос осей. Оси двух систем коорди-

нат параллельны и одинаково направлены (рис. 3.45). Коорди-

наты точки М

этих системах связаны зависимостью

х-\-а,

у'+Ь, х'

ха у'

уЬ, (1)

154

Гпава 3

где х,у — координаты точки М

системе Оху\

х\у'

— коорди-

наты точки М

системе О 'х 'у';

а,Ь

— координаты начала коор-

динат

О'системы

О'x'j^'в

системе Оху,

у'

О'(а.Ь)

М{х,у)

ix'.y')

х'

Рис. 3.45

2°.

Поворот осей. Обе системы координат имеют общее

начало и различаются направлением осей. Если положение сис-

темы О'х У'определяется относительно системы Оху углом по-

ворота осей

(рис. 3.46), то зависимость между координатами

точки М определяется по формулам

(2)

Рис. 3.46

xco^a-ysma^ y^xsina-^rycosa,

X =х cos а +

sin а, У = х sin+ у cos а,

У. Общий случай. Если системы Оху и O'x'j;' имеют раз-

личные начала и различно направленные оси (рис. 3.47), то за-

висимость между координатами точки М определяется по

формулам

X = X

cosa-/^\па-\-а^ у

х'smaл-у'cosaл-Ь. (3)

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

155

У^

М{х.у)

ix'.y')

\/(а

0'(а,Ъ)

Рис. 3.47

Новые координаты выражаются через старые по формулам

х'-(х-а)

со^а-^(у-Ь) sin а,

'=-

(х-а) sin а + (у-Ь) cos а. (4)

7.1.

Точка М имеет координаты х-Ъ,у --1. Найти ее ко-

ординаты, если начало координат перенесено в точку 0'(-2;5).

Решение. По условию х =3, у --1, а --2, Ь-5. Координаты

точки Мв новой системе

буjiyi:

х*-х-а-Ъ+2-5, у'-у-Ь--1-5^=^12.

7.2.

Найти координаты точки М

, если оси ко-

ординат поворачиваются на угол

ос

= 45°.

Решение. Координаты точки М даны в системе Оху. Вос-

пользуемся формулами (2)

,л/2 ,V2 ^ г- ,л/2^ ,V2

= х у , -2v2 =jc Vy .

Из решения системы находим, что х'--— ,у'-- ~ .

7.3.

Найти координаты точки М(1;2), если начало коорди-

нат перенесено в точку

0\-\,\)

и оси координат были поверну-

ты на угол а^ЗО"".

Решение. По условию задачих-\,у =2,

ЙГ

=-1,

а = 30°.

Воспользуемся формулами (3)

, ,73 ,1 . ,1 .4Ъ.

\ = х у 1, 2 = jc—+V + 1.

2 "^ 2 2 2

156

Гпава 3

Из решения системы находим, что х =

+ 2л/з , V3-2

=•

1 ' -^ 2

7.4. Путем параллельного переноса осей координат найти

координаты вершины параболы у = 2JC^-4X+9

привести

ее

урав-

нение к виду Y - аХ^.

Решение. Воспользуемся формулами (1). Подставив их в

уравнение параболы, получим у'л-Ь-2(х'+а)2-А(х'л-а)-^9

или у'

=^2х'^^А(а-\)х'^2а^

-Аа

Э-Ь,

Координаты нового начала координат неизвестны. Нахо-

дим их из условия равенства нулю свободного члена в новом

уравнении параболы и коэффициента при х\ то есть

2а^ -Аа

9-Ь

0 и (2-1 = 0. При этих условиях имеем а=1,

6 = 7. Уравнение параболы в новых осях 0\у имеет вид

у*

2х'^

График параболы показан на

рис.

3.48.

0\а,Ь)

Рис. 3.48

7.5. Составить уравнение равносторонней гиперболы, при-

няв ее асимптоты за оси координат.

Решение. Уравнение равносторонней гиперболы имеет вид

х^

-у^ =а2. Уравнения асимптот;; =±х. Здесь tga = ±

то есть

а= ±45°.

Примем а =45° (рис. 3.49). Воспользуемся формулами (2)

х=х'

00845°-;^'

sin45°,

^ = -Jz-,

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ

157

X Л-у

j;=x'sin45°+;;'cos45°,

^"""/^

Рис. 3.49

Подставляя значения х,уъ уравнение гиперболы, получим

л 2

{х-у) {х+у)

^а", откуда у =•

2 2

7.6. Выполнить параллельный перенос осей координат так,

чтобы в новой системе координат уравнение параболы приняло

канонический вид: а) x^-4x+j;+1

=0;

б)

J;^-3JC-2J^+10=0.

Решение, а) Выделим полный квадрат x^-4x+4+j^+l-4=(x-

2)^+>^-3=0. Введем теперь новые координаты х\у\ полагая

ХЧ-2, У =

J^'+3,

ЧТО соответствует параллельному перемеще-

нию осей на

две

единицы по оси Ох

на три по оси Оу.

коорди-

натах

X',

>^'уравнение параболы примет

вид:

х^+у -О или х^=-у'.

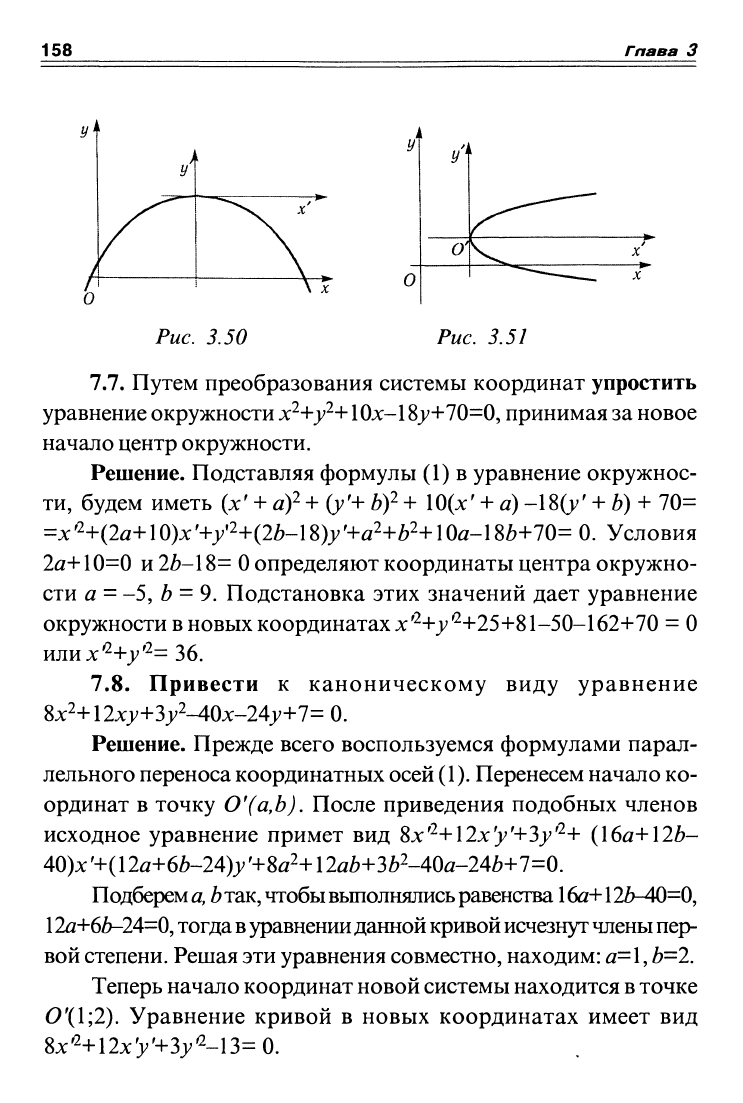
Поскольку правая часть отрицательна, то ветви параболы на-

правлены вниз (рис. 3.50).

б) Выделим полный квадрат >'^-2j;H-l-3x+10-l=(y-l)^-

Зх+9=0 и запишем уравнение в виде 9(у-1)^=3(х-3). Введем но-

вые координаты, полагая

j;=j;'+l,

х=х'+3, что соответствует

параллельному перемещению осей на

единицы по оси Ох и на

1 единицу по оси Оу (рис. 3.51). Тогда получим

>^'^=3х'

— кано-

ническое уравнение параболы.

158

Гпава 3

Рис. 3.50 Рис. 3.51

7.7. Путем преобразования системы координат упростить

уравнение окружности x^+y^-^lOx-lSy-^10=0, принимая за новое

начало центр окружности.

Решение. Подставляя формулы (1) в уравнение окружнос-

ти,

будем иметь (х' +

а)^

+0'+ bf

10(х'-^ a)-lS(y'+ b) + 70=

=х'^Ц2а-^10)х'+уЧ(2Ь-Щу'+аЧьЧ10а-18Ь+10= 0. Условия

2а+10=0 и 2Z?-18=

определяют координаты центра окружно-

сти а

-5, b = 9. Подстановка этих значений дает уравнение

окружности в новых координатах x'^+j'2+25+81-50-162+70 =

ияих^+у'^^Зб,

7.8. Привести к каноническому виду уравнение

Sx4\2xy+3y^-40x-24y+l= 0.

Решение. Прежде всего воспользуемся формулами парал-

лельного переноса координатных осей

(1).

Перенесем начало ко-

ординат в точку 0'(а,Ь), После приведения подобных членов

исходное уравнение примет вид 8x'^-M2x'j'+3j'^+ {I6a-^\2b-

40)x'+il2a+6b~24)y'-\-Sa4l2ab+3b^-40a-24b+l=0.

Подберем

а,

так,

чтобы выполнялись равенства

16а+12/ь40=0,

12^+66-24=0,

тогда в уравнении данной кривой исчезнут члены

пер-

вой

степени.

Решая эти уравнения совместно, находим: а=\,Ь=2.

Теперь начало координат новой системы находится в точке

0Х1;2).

Уравнение кривой в новых координатах имеет вид

8;с^+12х>'+Зз;МЗ=0.

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ 159

Чтобы избавится от члена, содержащего произведение коор-

динат х\у\ произведем поворот перенесенных осей на некоторый

угол а, согласно формулам (3), тогда получим (8 cos^ а +

sin^Q:

+ i2 cos а sin а )х "^+(-16 sinacosa+6 sinacosa +

+12cos2a42sin2a)x>''+(8sin2a:+3cos^a-12sinacosa)j;'M3 = 0.

Подберем угол ее так, чтобы коэффициент при

x"j^"

об-

ратился в нуль

-1 Osin

cos

а +12cos^ а -12sin^ а =

О,

откуда

6tg2a+5 tga-6=0.

Решая полученное квадратное уравнение относительно

2 3

tg а, находим:

igC)C-~

и tga=-—. Возьмем первое значе-

ние,

что соответствует повороту координатных осей на ост-

1 3

рыйугол. Зная tgа, находим cosa= и , i R^ ' sina =

tga 2

~ ~

Тогда уравнение кривой в системе х '\у "при-

tg'a л/Гз

156 .2

мет вид JC

^^2

j;^^

или -у^—

Мы получили кано-

ническое уравнение гиперболы с полуосями -у/— и

(рис. 3.52).

Рис. 3.52