Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

140 Г пава 3

Директрисами гиперболы

называются прямые

d^^d^^

парал-

лельные мнимой оси и отстоящие от

нее

на расстоянии

—.

Урав-

нения директрис ^ - ± - .

Отношение расстояния любой точки гиперболы до фокуса

к ее расстоянию до соответствующей этому фокусу директрисы

Y Т

есть величина постоянная, равная эксцентриситету

—^

-j-

= £ .

d^ «2

Фокальные радиусы r^r^ некоторой точки М(х,у) могут

быть найдены по формулам

= ±{гх - а\

г^

±(а + £х). (7)

Если полуоси гиперболы равны, то гипербола называется

равносторонней и ее уравнение имеет вид

х'-^у'=а\

(8)

Асимптотами равносторонней гиперболы служат биссект-

рисы координатных углов у = ± х.

Уравнение равносторонней гиперболы, отнесенной к своим

асимптотам, как к осям координат, имеет вид

- (9)

где ^ =

"Г"-

Каждая ветвь гиперболы (9) имеет вершину с равными по

абсолютной по величине координатами и удаленную от начала

координат на расстояние а = 42к •

Уравнение равносторонней гиперболы с асимптотами, па-

раллельными осям координат, имеет вид

ахЛ-Ь

cjc + a

где<2,

Ь,

с, d—постоянные коэффициенты.

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ

141

Уравнение (10) по формулам параллельного ереноса коор-

динатных осей может быть приведено к виду (9).

4°.

Параболой называется геометрическое место точек,

равноудаленных от данной точки, называемой ее фокусом и от

данной прямой, называемой

ее

директрисой

(рис.

3.35).

Рис, 3.35

Каноническое уравнение параболы имеет вид

/=2рх, (И)

где/7 — параметр параболы, равный расстоянию от фокуса до

директрисы.

Фокальный радиус любой точки параболы М(х,у) вычис-

ляется по формуле г=х+

—.

У параболы один фокус, следова-

тельно

одна директриса

^'=^~Z •

Эксцентриситет параболы равен

отношению расстояния любой ее точки от фокуса к расстоянию

до директрисы. На основании определения параболы имеем, что

эксцентриситет любой параболы равен единице ^ =

— =

Общее уравнение параболы, ось симметрии которой парал-

лельна оси ординат, имеет вид

= ax^+6x +

(12)

где

л,

Ь,

— постоянные коэффициенты.

142

Гпава 3

6.1.

Найти координаты центра

радиус окружности

Решение. Дополняя левую часть уравнения до полных квад-

ратов, получим x^-2x+l+j;2+8j+16 = 4 или (x-l)^+(j;+4)^ = 4.

Следовательно а- \,b--4,R-l.

6.2.

Составить

уравнение окружности, проходящей через три

данные точки v4(l;l), Д0;2) и С(2;-2).

Решение. Уравнение искомой окружности содержит три

неизвестных параметра

а,ЬиК,

которые следует определить.

Подставляя координаты точек А, ВяСв уравнение окружно-

сти (1), получим систему трех уравнений относительно неиз-

вестных

{2-af+{2-bf=R\

Вычтем из последнего уравнения сначала первое, потом —

второе уравнение, тогда получим: 2а-6Ь = 6, 4a-Sb

4, откуда

-3,

-2. Из первого уравнения находим, что R^ = 25. Сле-

довательно, уравнение искомой окружности имеет вид

(x+3)2+(j+2)2=25.

6.3.

Составить уравнение окружности, проходящей через

точку

А{1;9)

и касающейся оси Ох в точке В(4;0).

Решение. Делаем схематический чертеж (рис. 3.36).

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ 143

Замечаем, что ОВ

а = 4, ВС =

= R, так как перпенди-

куляр ВС к касательной Ох параллелен оси Оу и проходит че-

рез центр окружности С(а,Ь). Уравнение искомой окружности

примет вид {x-Ay-^iy-Ry- - R^. Подставляя в это уравнение ко-

ординаты точки

У4(7;9),

получим (7-4)^+(9-7?)^ =

7?^,

откуда

7? = 5. Следовательно, уравнение окружности примет вид

(х-4)2+0;-5)2=25.

6.4. Не выполняя построения, установить, как расположе-

ны относительно окружности x^+>'^+8x-4j^-29 =

точки:

А{4;3),

5(-1;2),

СИ;9).

Решение. Подставля координаты точки А в уравнение ок-

ружности, получим 16+9+32-12-29 = 16, следовательно, точка

А лежит вне окружности.

Подставляя координаты точки В, будем иметь 1+4-8-8-

-29

-40, следовательно, точка

лежит внутри окружности.

Подставляя координаты точки С, получим 16+81-32-36-

-29 =

О,

следовательно, точка

лежит на окружности.

6.5. Составить уравнение эллипса, зная, что он проходит че-

рез точки

его оси симметрии совпада-

ют с осями координат. Найти уравнения его директрис,

координаты вершин и фокусов, вычислить эксцентриситет и ве-

личины фокальных радиусов точки М.

Решение. Уравнение эллипса имеет вид (2). Точки М и N

принадлежат эллипсу, значит их координаты удовлетворяют его

уравнению. Подставляя их в уравнение эллипса, получим систе-

му двух уравнений относительно

а^

Ь^

(S.t^^l t^.^ = .. откуда

.-,5,*-5.

а О а о

2 2

Следовательно, искомое уравнение —

— = 1.

Величину с найдем из соотношения

с^

а^-Ь^

15-5 =10.

144

Гпава 3

Итак, a=vl5, 6=лУ5 и c~-s[)Ss. Эксцентриситет будет

л/lO л/б ^, . 2л/10 ^

г =

—т=

= —. Уравнения директрис: х-± . Вершины эл-

Vl5 3 *^ ^ "^ 2

липса (рис. 3.37): А^{^Ъ

fS)

^2(-Vl5 ,0), B^(0,^l

В^(0-^),

его фокусы:

F^(

VlO,

0), F^i-л/Го ,0). Фокальные радиусы точки

Мнаходим по формулам

(3):

г, = Vl5 - v2,

Г2

= лДЗ + V2 .

6.6. Расстояния одного из фокусов эллипса до концов его

большой оси, соответственно, равны 8 и 2. Составить канони-

ческое уравнение эллипса.

Решение.

Данные расстояния могут

бьггь

представлены фор-

мулами а-с = 2 и

а+с

= 8. Отсюда

2а

= 10,2с =

или а = 5, с = 3.

Так как

Ь^

а^-с^,

то Ь^= 25-9=16. Следовательно, уравнение

2 2

^ У 1

искомого эллипса —

— = 1.

25 16

^' / 1

6.7. Один из диаметров эллипса ~'^~'^^ имеет уравне-

9 16

ние

j;=-2x.

Найти уравнение сопряженного ему диаметра.

Решение. Здесь

а^

= 9,

Z?^

= 16, /:^ =

-1.

По формуле (5) на-

16 8

ходим, что

f<^2 "^

~Q.

= ~. Уравнение искомого диаметра име-

етвид у =Т^.

9(-2) 9

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ 145

6.8.

Оси

эллипса совпадают

осями координат

равны:

а= 10,6

1. Определить длину сопряженных полудиаметров

а'

Z?'H

направление диаметра

2Ь\

если известно, что диаметр 2а*

образует

осью

2а

угол 20°.

Решение. Уравнение эллипса

н =

1. Пусть уравне-

ние диаметра имеет вид

у-

к^

х.

Решая эти уравнения совмест-

но,

находим точки пересечения

10А:,

Х,^=±-7=

о=±

1,2

Д2=±-

фоОк^+1'

''' фоОк^+1

Учитьгоая,что

А:,

=tg(p^= tg 20°

0,364, длину первого полу-

диаметра находим по формуле расстояния между двумя точками

^ ' ^' ^ja^kf+b^

100(0,364)41

Длину второго полудиаметра находим по теореме Аполло-

ния (Ь')^=аЧЬ^-(а')^, откуда fe' =

7lOO

l-(2,82)' -9,59.

Угловой коэффициент сопряженного диаметра находим по

формуле (5)

к,=——

= -0,0275, tg(p

k,,

(р

= 178^25'

' а'к, 1000,364 ' ' вг 2. г

6.9. Составить уравнение гиперболы, зная, что ее оси со-

впадают с осями координат и гипербола проходит через точки

М(5;-2) и N(3

л/2

;

лУ2 )•

Найти уравнения директрис и вычислить

эксцентриситет гиперболы.

Решение. Координаты точки Ми 7Vдолжны удовлетворять

каноническому уравнению гиперболы

(6).

Подствляя их в урав-

нение гиперболы получим систему уравнений

146

25 4 18 2

1 1

Решая систему относительно --j и тт?

а о

17 , , 22

тт^':^-

Откуда

а^-11,

Ь^=

—-. Составляем

о 22 7

находим

Гпава 3

1 1

: уравнение гипер-

_ 22

Поскольку для гиперболы с^-а^+Ь^, то с -11 + — - —

с [W ^л/7

Тогда эксцентриситет будет равен £=

— =

J = 3 —-.

. а л/77

Уравнения директрис находим по формуле х

±—

£ 3

6.10. Гипербола проходит через точку М(12;3 v3 ) и имеет

^^1

асимптоты

--'z^

Составить уравнение гиперболы.

Решение. Запишем уравнения асимптот в общем виде

±—х, тогда

—

= - . Обозначим Ь= у и а = 2у, где у —

а а 2

коэффициент пропорциональности.

Так как точка М принадлежит гиперболе, то подставляя ее

координаты и значения аиЬв каноническое уравнение

(6),

полу-

144 27

чим —у -

Откуда у^ = 9, следовательно, а = 6, Ь-Ъ.

"'' '' .^ /,

Уравнение гиперболы примет вид

:7^""

"^ ~

^ •

6.11.

Вычислить площадь трапеции, вписанной в гиперболу

ху-6, если вершинами трапеции являются точки пересечения этой

гиперболы с прямыми х-^у+З =

О,

и x-^y-l- 0.

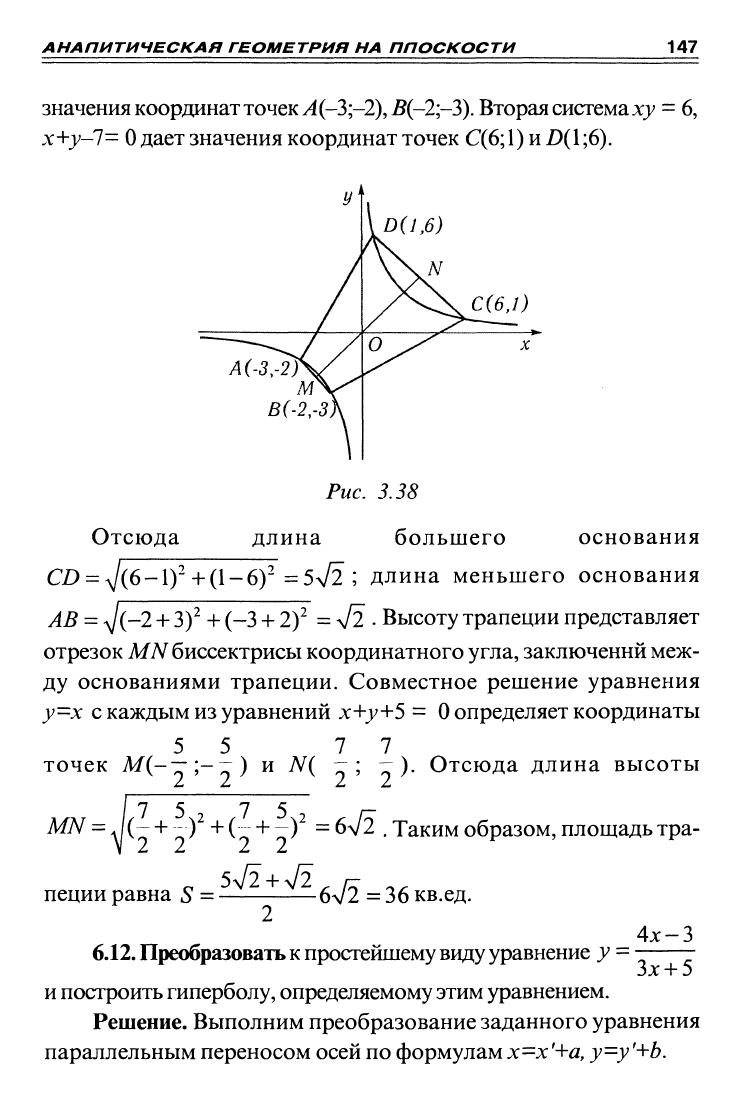
Решение. Строим чертеж

(рис.

3.38) и определяем координа-

ты вершин трапеции. Система уравнений ху - 6,

х-^у-^Ъ

дает

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ

НА

ППОСКОСТИ

147

значения координат точек У4(-3;-2), 5(-2;-3). Вторая система ху

- 6,

х-^у-1-

дает значения координат точек

С(6;

и D{\\6),

А(-Зг2)

В(-2гЗ

Рис.

3.38

Отсюда длина большего

основания

л/(6-1)"

-бУ =

5л/2

;

длина меньшего основания

АВ

л]{-2 +

3)^

+ (-3

2)^

= 72

Высоту трапеции представляет

отрезок МЛ/^ биссектрисы координатного угла, заключений меж-

ду основаниями трапеции. Совместное решение уравнения

у=х с каждым из уравнений х-^у+5

определяет координаты

5 7 7

точек М(-—;--)

и N( -; -).

Отсюда длина высоты

J( - + -Y + (- + -У

6л/2

Таким образом, площадь тра-

пеции равна

^tUlAe^^

36 кв.ед.

4х-3

6.12.

Преобразовать

простейшему

виду

уравнение

и построить гиперболу, определяемому

этим

уравнением.

Решение. Выполним преобразование заданного уравнения

параллельным переносом осей

по

формулам

х=х'-^а,

у=у'+Ь.

148

Гпава 3

5 4

Преобразуем уравнение

Ъху-^Ъу-

4х = -3 илиху+ —у —

х--\.

5 4

Используем подстановку {х '+«)(у '+Z?)+

—

(у

'л-Ъ)

— (х '+«)=

-1,

от-

4 5 4 5

куда X У+х

'(Z?

—) +7 '(^+ ~) =

« —

Ъ—аЪ-Л.

Условия преобра-

4 5

зования требуют, чтобы Ъ — =0 и а+— =0, тогда координаты

5 4

нового начала координат равны а- —' ^ ~ Т

•

^Р^ этом свобод-

4 5 5 4 5 4 29

ныйчлен принимает значение

А:=

—

(—) (—)т- -1= •

^ ЗМ^ 3 3 3 3 9

Заданное уравнение в системе хЮу имеет вид х[у - —— и

гипербола располагается во 11 и IV четвертях (рис. 3.39). Вер-

шины гиперболы находятся на биссектрисе 11 и IV координат-

пых углов на расстоянии

о,

= Л— от 0\

Рис. 3.39

6.13. Составить уравнение гиперболы, если известны точка

пересечения ее асимптот

0'(2;-3)

и одна из вершин .4(4;-!).

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ 149

Решение. Относительно системы координат

началом

точ-

ке

0'(2;-3)

пересечения асимптот условию соответствует урав-

пение гиперболы

у'~~~,.

Воспользуемся формулами

параллельного переноса начала координат

х'

х-2,

у'

j^+3.

Тог-

да уравнение гиперболы примет вид у

+ 3

= . Квадрат рас-

х-2

стояния от начала координат до вершины А находим по формуле

л^=(4-2)^+(-1+3)^= 8, тогда по формуле ^ = ~ находим, что

/с = 4. Следовательно, уравнение гиперболы примет вид

^^_ 4

-3JC

+ 10

y +

—

или

= .

х-2

^ х-2

6.14. Написать уравнение параболы, зная, что ось симмет-

рии

ее

совподает

осью Ох, а вершина—с началом координат и

расстояние от вершины до фокуса равно 5.

Решение. Каноническое уравнение параболы имеет вид

у^

2рх. По условию задачи

"Г

=5,

откуда /7=10. Уравнение

примет виду^=20х,

6.15. Составить уравнение параболы, если парабола сим-

метрична относительно оси

Оу^

вершина совпадает с началом

координат, а фокус находится в точке Д0;3).

Решение. Поскольку парабола симметрична относительно

оси Оу, то каноническое уравнение имеет вид х^

=•

2ру . По ус-

ловию

—

р-Ь.

Отсюда уравнение параболы х^

\2у,

6.16. Для параболы х^ = 2ру найти длину хорды, перпенди-

кулярной к оси Оу и проходящей через фокус.

Решение. Фокус параболы имеет координаты

F{0\

-г). Пусть