Буслаев А.П. Вероятностные и имитационные подходы к оптимизации автодорожного движения
Подождите немного. Документ загружается.


3.2.
Некоторые
вопросы
теории просачивания
71
Однолинейный
случай
не
представляет
интереса,
так как
при
Р
< 1
с
вероятностью
1
существует
бесконечно
много
закрытых
ребер
решетки
L
1
как
слева,
так
и
справа
от
на
чальной
вершины,
и,
следовательно,
О(р)
=
О,
если
р
<
1.
Таким
образом,
О(р)
=
О,
если
р
=
1.
Далее будем
считать,
что
d
~
2.
Доказано,
что
функция
Od(P)
не
убывает
по
d,
а
функция
Ре(
d)
строго
возрастает
по
d:
Pe(d
+
1)
<
Pe(d)
для
всех
d
~
1.
Следующая
теорема
утверждает,
что
имеет
место
не
тривиальный
критический
феномен
при
размерности
ре
шетки
2
и
более.
Теорема
1
([53]).
Если
d
~
2,
то
О
<
Pe(d)
<
1.
Суть
этой
теоремы
заключается
в
том,
что
в
случае
двух
и
более
измерений
существуют
две
фазы
процесса.
В
докри
тической
фазе,
когда
Pe(d),
каждая
вершина
почти
наверно
находится
в
конечном
открытом
кластере,
так что откры
тые
кластеры
почти
наверно
конечны.
В
сверхкр~тической
фазе,
когда
Р
>
Ре
(d),
каждая
вершина
имеет
строго
по
ложительную
вероятность
того,
что
эта
вершина
принад
лежит
бесконечному
открытому
кластеру,
так
что
почти
наверно
существует
по
крайней
мере
один
бесконечный
кла
стер.
Теорема
2 ([53]).
Вероятность
того,
что
существует
бесконечный
открытый
кластер,
удовлетворяет
следую
щему
соотношению:
ф(р)
==
{О,
если
Р
<
Pe(d),
1,
если
Р
>
Pe(d).
Оказывается,
что
если
d >
2,
то
при
Р
=
Ре(2)
с
вероят
ностью
1
не
существует
бесконечного
кластера.
Остается
открытым
вопрос
для
случая
d
~
3
и
Pe(d).
Ожидается,
что
бесконечного
кластера
не
существует.
Доказано,
что
бесконечный
кластер
в
случае
своего
су
ществования
единственен.

72
Глава
3.
Стохастические
модели
Приведем
некоторые
результаты,
связанные
со
сформу
лированными
теоремами,
и
отметим
некоторые
открытые
проблемы.
Во-первых,
чему
равно
численное
значение
Pe(d)?
Из
вестны
лишь
значения
Ре(1)
= 1
и
Ре(2)
=
~.
Во-вторых,
нетрудно
найти
нетривиальные
верхнюю
и
нижнюю
границы
Pe(d),
когда
d 2
3.
Имеет
место
соотно-
шение
1
Pe(d)
2
л(d)'
d 2
2;
(1)
здесь
Л(d)
= lim {a(n)l/n},
n--too
где
а(n)
есть
число
путей
(или
"самонепересекающихся
блу
жданий")
в
Ld,
имеющих
длину
n
и
начинающихся
в
началь
ной
вершине.
Точное
значение
л(
d)
неизвестно
для
d 2
2,
но
очевидно,
что
Л(d)
:::;
2d
-
1.
Действительно,
на
каждом
новом
шаге
самонепересекающегося
пути
имеется
не
более
2d
- 1
возможностей
выбора
в
силу
того,
что
следует
избе
гать
текущую
позицию.
Таким
образом,
а(n)
=
2d(2d
- 1)n-l.
В-третьих,
как
Pe(d)
ведет
себя,
когда
d
велико?
Из
неравенства
(1)
следует,
что
(2d
-
1)Pe(d)
2
1.
Доказано,
ЧТОРе(d)
rv
(2d)-1
при
d
--t
00.
Это
означает,
что
при
d
--t
00
реберное
просачивание
ведет
себя
так,
как
на
регу
лярно
ветвящемся
дереве,
каждая
вершина
которого
имеет
2d(1
+ 0(1))
потомков.

Глава
4
Имитационные
алгоритмы
и
вычислительные
эксперименты
4.1.
Схема
алгоритма
и
статистические
оценки
Дорога
представляется полосой
клеток
(рис.
4.1).
~
1
~
111
Рис.
4.1.
Модель
дороги
-
полоса
клеток
Каждая
клетка
-
это
часть
дороги,
которую
либо
зани
мает
АТС
вместе
с
динамическими
габаритами, либо она
свободна.
Через
равные
промежутки
времени
(такты)
каж
дое
АТС
с
определенной
вероятностью
р
перемещается
в
за
данном
направлении,
если,
кроме
того,
этому
движению
не
мешают
другие
АТС.
ДЛЯ
получения
характеристик
устано
вившегося
движения
будем
рассматривать
замкнутое
кле
точное
поле,
соответствующее
кольцевой
дороге
(рис.
4.3).
Перемещение
осуществляется
согласно
следующему
порядку
(рис.
4.
2)
за
один
такт
моделирования.
Рис.
4.2.
Типы
перемещения
АТС
1,1
I!
1
I1
, i
~
,
:1
1
I!
I
!
i
i"
ii
111
11
1;
'1
1,
I
:1
, 1
74
Глава
4.
Имитационные
алгоритмы
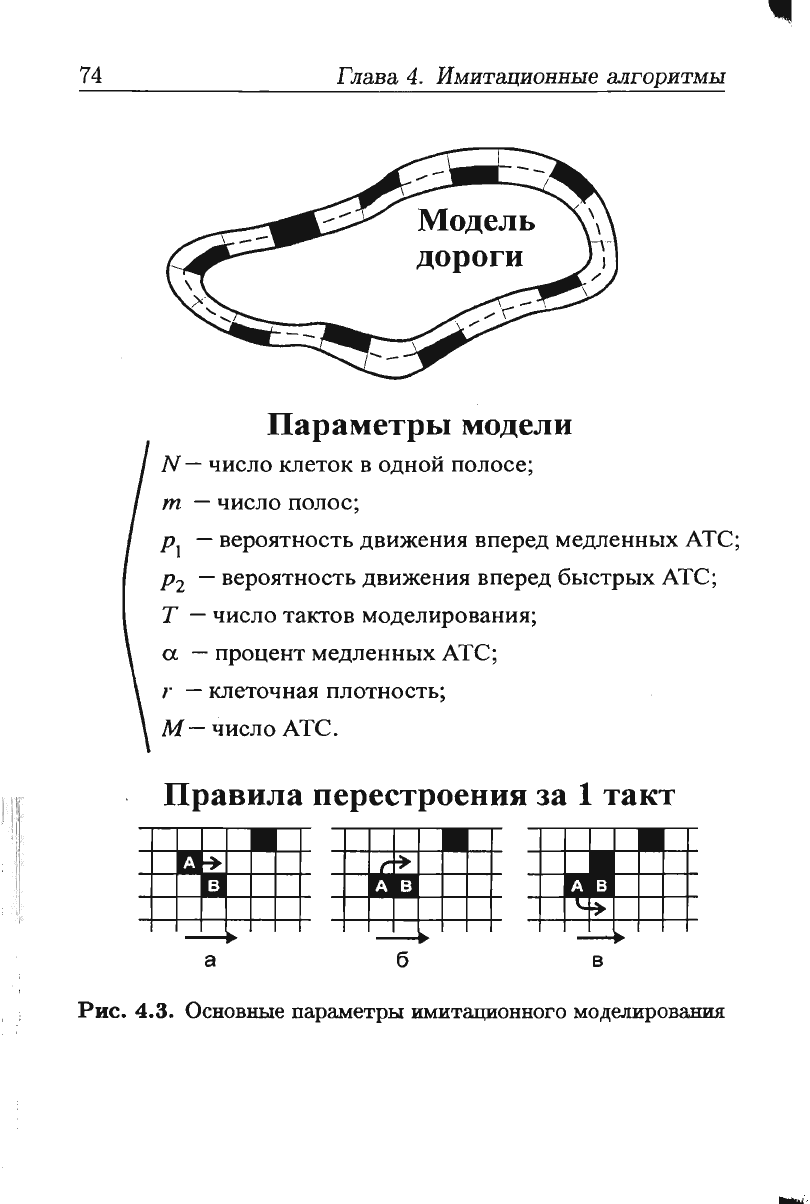
Пара
метры
модели
N -
число
клеток
в
одной
полосе;
т
-
число
полос;
Р.
-
вероятность
движения
вперед
медленных
АТС;
Р2
-
вероятность
движения
вперед
быстрых
АТС;
Т
-
число
тактов
моделирования;
а
-
процент
медленных
АТС;
,.
-
клеточная
плотность;
М
-
число
АТС.
Правила
перестроения
за
1
такт
а
б
в
Рис.
4.3.
Основные
параметры
имитационного
моделирования

4.
1.
Схема
алгоритма
и
статистич:еские
оценки
75
(1)
Параметры
модели:
lV
--
количество
клеток
на
одной
полосе
(длина
до
роги);
т
--
число
полос;
Т--
клеточная
плотность
(доля
занятых
клеток);
М--
количество
АТС
на
дороге
М,
т
=
NЛ:m;
(2)
на
lV
х
т
ячеек
(клеток)
случайным
образом
разбра
сываются
М
автомобилей,
каждый
из
которых
имеет
свой
номер;
(З)
в
каждый
момент
времени
определен
двумерный
мас
сив
координат
на
дороге
каждого
из
М
АТС;
(4)
перебираются
все
АТС
от
1-го
до
М-го,
для
которых
моделируется
вектор"
намерений"
передвижения
в
со
ответствии
с
заданными
вероятностями;
(5)
по
установленным
правилам
(рис.
4.2)
и
в
соответ
ствии
с
вектором"
намерений"
Р
=
(р!,
Р2)
осуществля
ется
преобразование
конфигурации
автомобилей
на
дороге;
(6)
алгоритм
прокручивается
по
времени
с
параллельным
процессом
вычисления
следующих
стохастических
по
казателей:
(а)
вектора
скоростей
Pi,
i
Е
М
перемещения
каждого
А
ТС
в
потоке.
Следует
ожидать,
что
если
вектор
на
мерений
постоянен
Pi
=
Р,
то
в
силу
симметрии р
=
Pst,
0<
Pst
<
Р;
(б)
статистической
оценки
интенсивности
qT
за
т
тактов:
фиксируются
клетки
с
одинаковой
первой
координа
той
i
o
Е
{1,
...
, lV};
суммируется
количество
qT
АТС,
побывавших
в
клетках
iо-уровня
за
время
Т,
берется
среднее
по
сериям
длины
Т;
76
Глава
4.
Имитационные
алгоритмы
(в)
статистической
оценки
,
плотности
на
фрагменте
длины
l
(l
< N):
прямоугольный
фрагмент
из
l
х
т
клеток,
на
котором
в
каждый
момент
времени
подсчи
тывается
количество
АТС
PL;
затем
берется
среднее
по
большому
времени
PL;
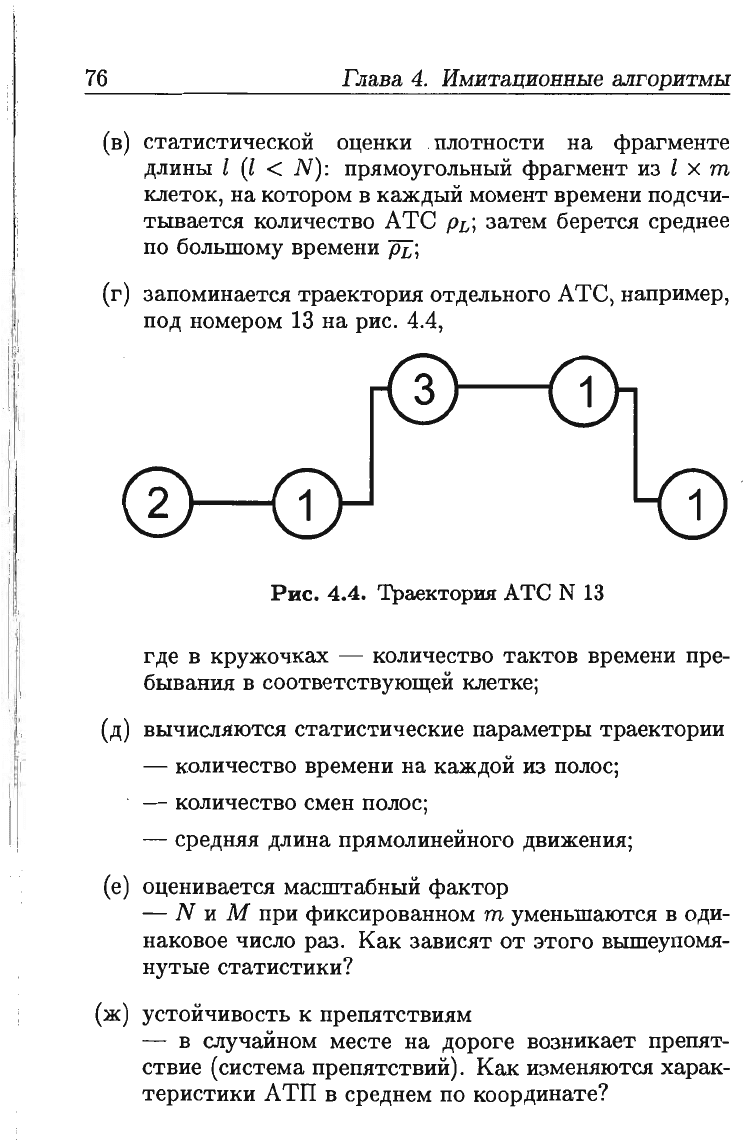
(г)
запоминается
траектория
отдельного
АТС,
например,
под
номером
13
на
рис.
4.4,
Рис.
4.4.
Траектория
АТС
N
13
г
де
в
кружочках
- количество
тактов
времени
пре
бывания
в
соответствующей
клетке;
(д)
вычисляются
статистические
параметры
траектории
-
количество
времени
на
каждой
из
полос;
- количество
смен
полос;
-
средняя
длина
прямолинейного
движения;
(е)
оценивается
масштабный
фактор
- N
и
М
при
фиксированном
т
уменьшаются
в
оди
наковое
число
раз.
Как
зависят
от
этого
вышеупомя
нутые
статистики?
(ж)
устойчивость
к
препятствиям
-
в
случайном
месте
на
дороге
возникает
препят
ствие
(система
препятствиЙ).
Как
изменяются
харак
теристики
АТП
в
среднем
по
координате?

/ 4.2.
Программная
реализация
77
4.2.
Программная
реализация
v
имитационнои
модели
Имитационная
стохастическая
модель
движения
реали
зована
в
виде
алгебраического
кода
в
объектно-ориентиро
ванной
среде
Borland Delphi.
Исходными
данными
модели
являются:
N -
количество
клеток
на
одной
полосе,
т
-
количество
полос,
т
-
плотность
потока,
k -
число
типов
АТС,
а
=
(аl,
... , ak) -
состав
потока,
Pi
-
вероятности
намерений
движения
вперед
для
i-го
типа
АТС,
i =
1,
...
, k.
Для
простоты
изложения
в
дальнейшем
положим
k = 2 .
.
Это
означает,
что
соответствующая
модель
учитывает
рас
слоение
потока
на
два
уровня:
быстрые
и
медленные
АТС.
Конструкция
модели
позволяет
провести
более
тонкий
ана
лиз
влияния
структуры
потока
на
его
динамику,
но
на
дан
ном
этапе
изложения
мы
остановимся
на
двух
типах
АТС.
В
этом
случае
можно
считать,
что
величина
параметра
а
-
доля
медленных
АТС.
По
исходным
данным
определяются
значения
внутрен
них
переменных
и
массивов
модели:
i -
номер
клетки
по
длине
дороги
в
направлении
дви-
жения,
1
::;
i
::;
N;
j -
номер
полосы,
1
::;
j
::;
т;
М
-
число
АТС,
М
= N
'т-т;
l-
номер
АТС,
l =
1,
...
,
М;
ММ
-
число
медленных
АТС,
ММ
=
а·
М;
type[l] -
тип
АТС
N l;
p[l] -
массив
вероятностей
появления
"намерений"
АТС
совершить
движение
вперед
для
АТС
N
l:
[
l]
=
{Рl'
для
медленных,
р
Р2,
для
быстрых;
m[i,
j]
-
массив
состояния
клетки
(i,
j)
на
текущем
такте:

I
I
78
Глава
4.
Имитационные
алгоритмы
пустая
на
текущем
такте;
m[i,
j)
=
иначе,
l -
номеру
АТС,
!
О,
если
клетка
(i,
j)
нахо,цящегося
в
клетке
на
текущем
такте;
m2[i,j) -
массив состояния
клетки
(i,j)
на
пре,цы,цущем
такте:
пустая
на
пре,цы,цущем
такте;
m2[i,
j)
=
иначе,
l -
номеру
АТС,
!
О,
если
клетка(i,
j)
нахо,цящегося
в
ней
на
пре,цы,цущем
такте;
sobitie[l]
-
количество
перемещений
на
клетку
впере,ц,
совершенных
АТС
N l
за
текущее
число
шагов;
sobitie2[l]
-
количеству
перестроений
в
сосе,цнюю
по
лосу,
совершенных
АТС
N l
за
текущее
число
шагов
.
На
начальном
шаге
мо,целирования
генерируется массив
m[i,j):
-
М
раз
разыгрывается
равномерно
распре,целенная
в
интервале
[1,
N .
т]
случайная
величина,
в
соответствии
с
которой
отмечаются
занятые
клетки
клеточного
поля
по
числу
АТС.
Помеченные
клетки
нумеруются
1,
...
,
М,
-
случайным
образом
генерируется
перестановка
(
1 2 3
...
ММ
мм
+ 1 .
,.
М)
jl
12
Jз
...
jMM
jMM+1
.
..
jM
'
В
соответствии
с
которой
в
отмеченные
клетки
расставля
ются
номера
АТС,
причем
jl,12,jз""
,jMM
соответствуют
ме,цленным
АТС,
рис.
4.5.
N2
клетки
1
2 3
4
5
6
..
.
полоса
2
8188
.98
...
полоса
1
--
.2.
••
.
..
Рис.
4.5.
Начальное
состояние
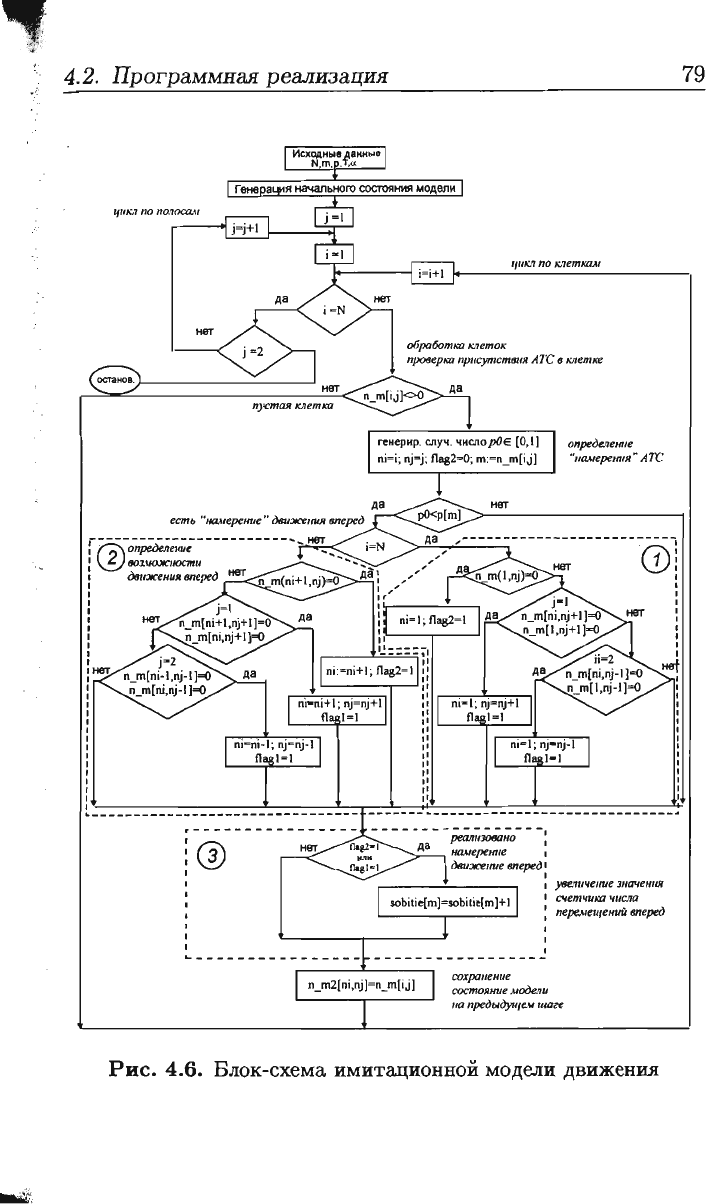
Затем
происхо,цит
циклический
пересчет
тактов
мо,це
лирования,
блок-схема
которого
показана на
рис.
4.6.
'
<;,
~
}
~
;i
/;.-"
~/
4.2.
Программнан
реализация
пустая клетка
цт:..,
по
клеткам
06fЮбоm,,-а
клеток
nfЮ"CрIШ
nр"cymстfl1/Я
АТС
в
клетке
оnределеЮlе
"намерения"
АТС
У8е.:llIчеlше
значtUIIR
cvеmчшш
числа
:
nере...,ещенuU
tRJeред
сохранение
состояние
моделu
1Iа
nредыдуще..:w
UШ2е
Рис.
4.6.
Блок-схема
имитационной
модели
движения
79

80
Глава
4.
Имитационные
алгоритмы
N!!
клетки
1
2
3
...
N-2
N-1
N
Время
j
1
87_
..
.
~
2
.1~1.
81_
Время
j+1
1
828.
•
7_
...
823
•
2
8Н18
...
Рис.
4.7.
Состояние
модели
на
соседних
тактах
j
и
j + 1
Опишем
более
по,цробно
блок
обработки
непустой
клетки.
Разыгрывается
вероятность
РО
намерения
дви
гаться
вперед.
Если
Ро
<
р,
то
это
означает,
что
автомо
биль
принял
решение
,цвигаться
впере,ц
.
Далее
начинается
обработка
информации
о
клетках
расположенного
впереди
сечения.
Если
впереди
клетка
свобо,цна
n_т[i
+
1]
=
О,
то
АТС
перемещается
вперед
на
о,цну
клетку
i
:=
i +
1,
(если
i =
N,
то
полагаем
i + 1 = 1).
Например,
дЛЯ
АТС
N 7
на
рис.
4.7
счетчик
передвижений
вперед
sobitie(7)
увеличива
ется
на
1.
По
окончании
обработки
клетки
i,
перехо,цим
к
обра
ботке
клетки
i + 1
и
так
,цо
N.
После
завершения
ци
кла
счета
происхо,цит
переприсваивание
элементов
массива
n_т
(шаг
j)
элементами
массива
n_т2
,цля
обработки
про
це,цуры
на
шаге
j +
1.
В
файл
записывается
сле,цующая
информация
(она
же
отображается
на
экране):
•
частота
отсутствия
АТС
в
клетке
контроля;
•
частота
движения
каждого
АТС;
•
частота
,цвижения
всего
потока
АТС;
•
количество
проше,цших
тактов
мо,целирования;
•
,цлина
,цороги
в
клетках;
