Буслаев А.П. Вероятностные и имитационные подходы к оптимизации автодорожного движения
Подождите немного. Документ загружается.


Глава
3
Стохастические
модели
при
исследовании
больших
систем
3.1.
Качественные
свойства
цепей
Маркова
и
общие
теоремы
в
качестве
математической
модели
автотранспортного
потока
далее
будем
применять
подход,
связанный
с
цепями
Маркова.
Приведем
определение
используемых
нами
ПОНJIтий
тео
рии
случайных
процессов
[28,36].
Случайный
процесс
представляет
собой
семейство
слу
чайных
величин
Xt,
где
t -
параметр,
принадлежащий
со
ответствующему
множеству
Т.
Если
Т
= (0,1,2,
...
),
то
говорят,
что
(Xt)
является
случайным
процессом
с
дискрет
ным
временем.
Пространство
состояний
S -
это
простран
ство,
которому
принадлежат
все
возможные
значения,
при
нимаемые
всеми
случайными
величинами
Xt.
В
случае,
если
S = (0,1,2,
...
),
процесс
относят
к
классу
целочисленных
процессов,
или
процессов
с
дискретным
пространством
со
стояний.
В3JКной
чертой
случайного процесса
является
зависи
мость
между
случайными
величинами
Xt,
t
Е
Т.
Харак
тер
этой
зависимости
определяется
заданием
совместных
функций
распределения
для
каждого
конечного
семейства
Xtl
,
...
,Xt
n
случайных
величин
процесса.

62
Глава
3.
Стохастические
модели
Марх:овсх:ий
процесс
-
это
процесс,
обладающий
тем
свойством,
что
если
известно
значение
случайной
величины
Xt,
то
значения
Ха,
S > t,
не
зависят
от
Х
щ
и
< t;
другими
словами,
вероятность
любого
события,
связанного
с
бу
ду
щим
поведением
процесса,
при
условии,
что
его
настоящее
состояние
точно
известно,
не
изменится,
если
учесть
до
полнительную
информацию
относительно
ПРОIПJIого
этого
процесса.
Дискретная
марковская
цепь
(Х
п
)
представляет
собой
марковский
случайный
процесс,
пространство
состояний
которого
счетно
или
конечно,
а
множество
индексов
т
=
(0,1,2,
...
) = Z+.
Часто
пространство
состояний
про
цесса
удобно
отождествлять
с
множеством
неотрицатель
ных
целых
чисел
(0,1,2,
...
).
Говорят,
что
в
момент
вре
мени
n
система
находится
в
состоянии
i,
если
Х
П
= i.
При
анализе
марковских
цепей
вводится
в
рассмотрение
веро
ятность
перехода
за
один
такт
времени
из
состояния
i
в
состояние
j
(называемая
одноmаговой
переходной
вероят
ностью)
.
Когда
одношаговые
переходные
вероятности
не
зависят
от
временной
переменной
(от
значения
n),
говорят,
что
.марх:овсх:ая
цепь
стационарна.
Далее
мы
будем
иметь
дело
только
с
такими
марковскими
цепями.
Обычно
веро
ятности
перехода
за
один такт
времени
из
состояния
i
в
состояние
j
~;
объединяют
в
матрицу
р=
II~jll,
называемую
матрицей
переходных
вероятностей
марков
ской
цепи.
Пусть
~;
(n)
-
вероятность
того,
что
процесс
перей
дет
из из
состояния
i
в
состояние
j
за
n
тактов
времени.
Говорят,
что
состояние
j
достижи.м.о
из
состо.яни.я
i,
если
~j(n)
>
О
дм
нех:оторого
целого
'Числа
n
~
О,
т.е.
веро
.ятность
того,
'Что
процесс
за
n
тах:тов
попадает
из
со
сто.янu.яi
в
состо.яние
j,
положительна.
Если
существует
состояние
j,
такое,
что
оно
достижимо
из
состояния
i,
а
со
стояние
i
из
состояния
j
не
достижимо,
то
состояние
i
назы
вается
несущественны.м..
Состояние,
не
являющееся
несу
щественным,
называется
существенны.м..
Два
состояния
i
и

3.1.
KaqeCTBeHHble
свойства
цепей
Маркова
63
j
называются
сообщающи.м:uся,
если
состояние
j
достижимо
ИЗ
состояния
i
и
состояние
i
достижимо
из
состояния
j.
Будем
предполагать,
что
все
состояния
цепи
существенны.
Все
множество
состояний
можно
разбить
на
классы
эквива
лентности.
Состояния
объединяются
в
один
класс,
если
они
сообщаются
друг
с
другом.
Из
состояния,
принадлежащего
одному
классу,
попасть
в
другой
класс
невозможно,
так
как
иначе оба
класса
входили
бы
в
один
класс
эквивалентности.
Говорят,
что
мар-х:овс-х:ая
цепь
неnриводима
(нераЗ.ltожима),
если
введенное
отношение
эквивалентности
порождает
один
класс.
Другими
словами,
процесс
неприводим,
если
все
его
состояния
сообщаются
друг
с
другом.
Определим
период
состояния
i,
далее
обозначаемый
d(i),
как
наибольший
общий
делитель
всех
целых
чисел
n
~
1,
для
которых
Pij(n) >
о.
(Если
~j(n)
=
О
при
всех
n
~
1,
то
по
определению
d(
i) =
о.)
Пусть
fi(n) -
вероятность
того,
что
отправляясь
из
со
стояния
i,
система
впервые
возвращается
в
это
состояние
через
n
переходов.
Состояние
i
называется
возвратным,
00
если
L:
fi(n) =
1.
n=l
Это
означает,
что
состояние
яв.ItЯется
возвратны"",
то-
гда и
то.ltь-х:о
тогда,
-х:огда
вероятность
вернутьс.я
в
исход
ное
состояние
i
nОС.ltе
не-х:оторого
'l'Cоне'Чного
'ЧиС.ltа
шагов
равна
единице.
Состояние
i
называется
ну.ltевы"""
если
~i
(n)
-+
О
при
n -+
00,
и
ненулевым
в
противном
случае.
Невозвратное
состо,яние
всегда
,яв.ItЯетс,я
ну.ltевьш.
Имеет
место
следующее
утверждение
[36].
Теорема
(о
СО.ltидарности.)
В
неnриводимой
цеnи
Мар
кова
все
состо,янш
nрuнад.ltежат
одно.м.у
тиnу.
ЕС.ltи
хотя
бы
одно
возвратно,
то
и
все
возвратны;
ес.ltи
хот,я
бы
одно
НУ.ltевое,
то
и
все
НУ.ltевые;
ес.ltи
хотя
бы
одно
nерuодu'Чно,
то
u
все
nериодu'Чны
с
тем
же
периодом.
Имеет
место
следующая
[36]
Теорема
(об
зргодu'Чности).
Пусть
марковс'I'Cа.я
цепь
неnриводима
и
неnериоди'Чна
и
существует
состо,яние
та-

i
i:
;
I ,
i :
! i
64
Глава
3.
Стохастические
модели
"о
е,
'Что
вре.м.я
возвращенu.я
в
зто
состояние
u.мeeт
"оне'Ч
ное
математи'Чес"ое
ожидание
(ес.л.и
'Чuс.л.о
состояний
"0-
не'Чно,
то
зто
ус.л,овие
выnо.л.нено
всегда).
Тогда
и
то.л.ько
тогда
д.л,.я
.л.юбы.х
i
и
j,
i, j = 0,1,2,
...
существуют
не
за
вислщие
от
i
nо.л,ожите.л.ьные
nреде.л.ы
(стационарные
ве
роятности
состояний)
lim Pij(n) =
Р
;
>
О.
n~OO
Вектор
~
i = 0,1,2,
..
. )
является
единственным
реше
нием
системы
уравнений
{
ЕР
'
=
1,
}
. 1 3
з=
.
Р
;
=
Е
PkP
kj
, j =
0'1'2'
....
k=O
в
классе
последовательностей,
образующих
абсолютно
схо
дящиеся
ряды.
Мар"овс"а.я
цепь,
удовлетворяющая
вышеприведенной
теореме
называется
эргодической,
а
система
уравнений
определяет
стационарные
вероятности
состояний
цепи
Маркова.
В
случае,
если
число
состояний
цепи
Маркова
конечно,
стационарные
вероятности
состояний
системы
определя
ются
конечной
системой
линейных
уравнений.
При
этом
каждому
состоянию
цепи
соответствует
уравнение,
причем
любое
из
уравнений
системы
является
следствием
осталь
ных
[36],
и
ранг
матрицы
на
единицу
меньше
числа
неиз
BecTHых.
Следовательно
вышеприведенная
система
опреде
ляет
стационарные
вероятности
с
точностью
до
константы,
которую
легко
найти
из
условия,
'Что
сумма
стационарных
вероятностей
всех
состояний
цепи
равна
1.
Другим
классом
марковского
процесса
является
цепь
Мар"ова
с
дискретны,м
,множеством
состояний
и
непре
рывным
временем,
характеризующаяся
тем,
что
изменения
ее
состояний
осуществляются
в
произвольные
моменты
вре
мени.

3.2.
Некоторые
вопросы
теории
проса'Чивания
65
Пусть
~j(t)
-
вероятность
того,
что
рассматриваемая
цепь
Маркова
в
момент
времени
t
находится
в
состоянии
j
при
условии,
что
при
t =
О
она
находилась
в
состоянии
i.
Имеет
место
следующая
[36]
Теорема.
Пусть
,мар'К:овска.я
'Цепь
с
пеnерерывпы,м
вре
менем
и
ко1tечны,м
,м1tожество,м
состоя1tиu
пеnриводи,ма,
nриче,м
вре.м.я
nребыва1tш
'Цепи
в
каждо,м
состоянии
и,меет
uеnрерывпое
расnредедепие
с
ко1tе'Ч1tы,м
средпи,м.
Тогда
существуют
пе
зависящие
от
i
nодожитедь1tые
предеды
(ста'Циопарпые
вероят1tости
состоя1tиu)
для
любых
i,j
=
0,1,2,
...
,
т
(т
-
число
состояний),
удовдетворяющие
систе,ме
дипейпых
уравпепии
3.2.
Некоторые
вопросы
теории
просачивания
Монография
[53]
посвящена
математической
"теории
просачивания"
.
В
теории
просачивания
используется
модель
случайной
среды,
представляющая
собой
сетку
на
плоскости.
Задается
число
р,
О
~
Р
~
1.
Каждое
ребро
сетки
с
вероятностью
р
открыто
и
с
вероятностью
1 -
р
закрыто.
Для
рассма
триваемой
сетки
используется
физическая
интерпретация,
в
соответствии
с
которой
ограниченная
часть
сетки
рассма
тривается
как пор
истый
камень,
в
поры
которого
может
проникать
вода.
Часть
сетки,
соответствующая
камню,

66
Глава
3.
Стохастические
модели
представляет
собой
граф,
вершина
которого
считается
на
моченной
водой
тогда
и
только
тогда,
когда
в
данном
графе
существует
путь
до
данной
вершины,
причем
этот
путь
проходит
только
через
открытые
ребра
графа.
Если
ис
ключить
из
рассматриваемого
графа
закрытые
ребра,
то
получается
подграф,
структура
которого
подлежит
иссле
дованию
с
учетом
ее
зависимости
от
значения
р.
О
дной
из
решаемых
задач
является
вычисление
вероят
ности
того,
что фиксированная
вершина
будет
намочена.
Изучаются
также
следующие
обобщения
рассматриваемой
модели:
"смешанная
модель"
,
в
которой
могут
закрываться
как
ребра,
так
и
вершины;
анизотропная
модель,
в
которой
вероятности
закрытия
разных
ребер
различны;
модель,
в
которой
состояния ребер
зависимы
и
др.
Делаются
обоб
щения
на
многомерную
сетку.
Обсуждается
связь
рассма
триваемых
моделей
с
статистической
физикой,
теорией
на
дежности
и
другими
областями.
Приводимая
в
[53]
библио
графия
по
теории
просачивания
включает
работы,
опубли
кованные,
начиная
с
1957
года,
который
считается
годом
рождения
теории
просачивания
(Brodbent
S.
R.
, Hammers-
ley
J.
М.
Percolation processes
1.
Cristals and mazes. Proceed-
ings of the Cambridge Philosophical Society
53,
629-641).
Предположим,
что
пористый
камень
погружен
в
сосуд
с
водой.
С
какой
вероятностью
центр
камня
окажется
намоченным?
В
двумерном
случае
соответствующая
мо
дель
описывается
следующим
образом.
Пусть
z2
-
плос
кая
квадратная
решетка
и
число
р
удовлетворяет
условию
О
~
Р
~
1.
С
вероятностью
р
каждое
ребро
решетки
от
крыто
и
с
дополнительной
вероятностью
закрыто
незави
симо
от
состояния
других
ребер.
Ребра
решетки
Z2
соот
ветствуют
внутренним
проходам
камня
и
параметр
р
есть
доля
проходов,
достаточно
широких
для
того,
чтобы
вода
могла
пройти
через
них.
Камень
моделируется
большой
ко
нечной
частью
решетки
z2.
Модель
камня
представляет
со
бой
некоторый
связанный
подграф
Z2
(рис.
3.1).
При
по
гружении
камня
в
воду
вершина
х
внутри
камня
намокнет
в
том
и
только
в
том
случае,
если
существует
путь
в
Z2
от
..,
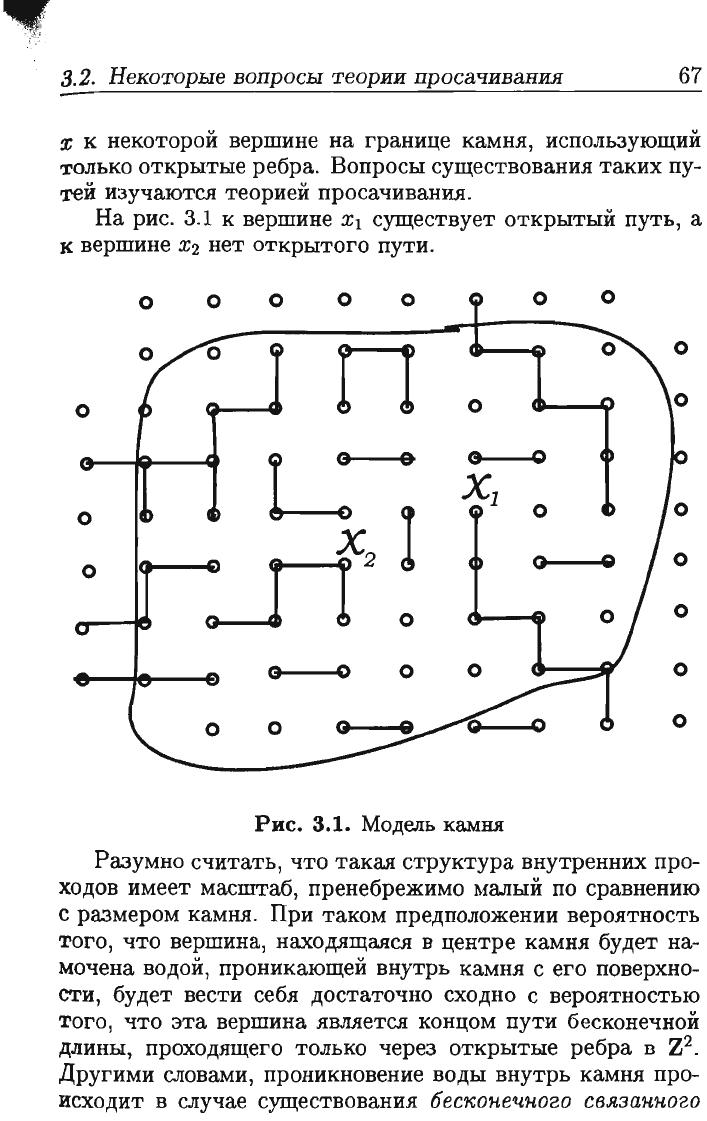
3.2.
Некоторые
вопросы
теории
просачивания
67
,;
к
некоторой
вершине
на
границе
камня,
использующий
только
открытые
ребра.
Вопросы
существования
таких
пу
тей
изучаются
теорией
просачивания.
На
рис.
3.1
к
вершине
Хl
существует
открытый
путь,
а
к
вершине
Х2
нет
открытого
пути.
о
о
о
о
о
о
о
о
п
о
о
L:
е
в
о
Х
1
О
Х
2
1
1
о
о
1
о
о
о
о
о
о
о
о
о
Рис.
3.1.
Модель
камня
Разумно
считать,
что
такая
структура
внутренних
про
ходов
имеет
масштаб,
пренебрежимо
малый
по
сравнению
с
размером
камня.
При
таком
предположении
вероятность
того,
что
вершина,
находящаяся
в
центре
камня
будет
на
мочена
водой,
проникающей
внутрь
камня
с
его
поверхно
сти,
будет
вести
себя
достаточно
сходно
с
вероятностью
того,
что
эта
вершина
является
концом
пути
бесконечной
длины,
проходящего
только
через
открытые
ребра
в
z2.
Другими
словами,
проникновение
воды
внутрь
камня
про
исходит
в
случае
существования
бес~оnечnого
С8лзаnuого

. !
68
Глава
3.
Стохастические
модели
'К.ластера
от'Крытых
ребер.
Когда
такие
бесконечные
кла
стеры
существуют?
С
вероятностью
1
все
открытые
кла
стеры
конечны,
когда
Р
мало.
При
достаточно
больших
Р
с
вероятностью
1
существует
бесконечно
большой
кластер
для
достаточно
больших
р.
Другими
словами,
существует
критическое
значение
Ре,
такое,
что
при
Р
>
Ре
все
откры
тые
кластеры
конечны,
а
при
Р
>
Ре,
с
вероятностью
1
су
ществует
бесконечный
открытый
кластер
.
Используя
физические
термины,
можно
сказать,
что
при
намачивании
камня
имеет
место"
поверхностный
эффект"
,
если
доля
открытых
ребер
мала,
и
"объемный
эффект",
если
доля
открытых
ребер
достаточно
велика.
Описанный
процесс
называется
"реберным
просачива
нием
на
конечной
решетке".
Это
наиболее
изученный
тип
процесса
просачивания.
Другим
типом
процесса
просачивания
является
"вер
шинная
модель
просачивания,"
в
которой
не
ребра,
а
вер
шины
объявляются
открытыми
или
закрытыми.
Обобщение
модели
просачивания
может
осуществляться
в
нескольких
направлениях:
1)
"с.мешанные
моде.tl,'и",
в
которых
как
ребра,
так
и
вер
шины
могут
блокироваться;
2)
анизотропные
моде.ли,
в
которых
прямой
поток
воз
можен
между
парами
очень
удаленных
друг
от
друга
вер
шин
(в
этой
модели
используется
граф,
вершины
которого
могут иметь
бесконечную
степень,
т.е.
вершине
может
со
ответствовать
бесконечное
множество
смежных
с
ней
вер
шин);
3)
зависимое
nроса'Чиванuе,
при
котором
вероятности
состояний
различных
ребер
не
являются
независимыми.
Модель
просачивания
может
быть
обобщена
и
в
других
направлениях.
В
дальнейшем
будем
говорить
о
реберном
просачивании
на
Zd.
Дадим
основные
определения
и
введем
обозначения.
В
дальнейшем
через
d
обозначается
размерность
nро
цесса.
Обычно
считают,
что
d
~
2.
Однако,
пока
пред-
,

3.2.
Некоторые
вопросы
теории
проса"lивания
69
полагаем
лишь,
чтоd
~
1.
Будем
обозначать
через
Z =
{
...
,
-1,
0,1,
..
. }
множество
всех
целых
чисел и
через
Zd
множество
всех
векторов
с
целыми
координатами.
Для
х
Е
Zd
через
Xi
обозначается
i-я
координата
Х.
Расстояние
б(х,
у)
от
Х
до у
определяется
по
формуле
d
о(х,
у)
= L
IXi
-
Yil·
i=l
Можно
превратить
zd
в
граф,
называемый
d-мерной
ку
бической
решеткой,
добавлением
ребер
между
всеми
па
рами
Х,
у
точек
Zd,
для
которых
о(х, у)
=
1.
Эту
ре
шетку
обозначают
через
Ld.
В
терминах
теории
графов
L
d
=
(Zd,
E
d
),
где
Zd
-
множество
вершин
решетки
L
d
,
а
E
d
-
множество
ее
ребер.
Решетку
Ld
часто
предста
вляют
себе,
как
граф,
размещенный
в
R
d
,
с
ребрами,
явля
ющимися
отрезками
между
соединяемыми
ими
вершинами.
Если
о(х,
у)
=
1,
то
говорят,
что
Х
и у
смежны.
В
этом
случае
пишут
Х
rv
у
И
обозначают
ребро,
соединяющее
Х
с
У,
через
<
х,
у
>.
Ребро
е
инцидентно
концевой
вер
шине
е.
Обычно
вершины
обозначают
такими
буквами,
как
'и,
V,
W,
Х,
у,
а
ребра
обычно
обозначают
как
е,
f.
Пусть
р
и
q
таковы,
что
О
:s;
Р
:s;
1
и
р
+ q =
1.
Каждое
ребро
решетки
L
d
с
вероятностью
р
открыто
и
с
вероят
ностью
q
закрыто
независимо
от
состояния
других
ребер
.
Более
формально
вероятность
определяется
путем
задания
соответствующей
вероятностной
меры
на
множестве
эле
ментарных
исходов,
находящихся
во
взаимно
однозначном
соответствии
с
множеством
состояний
решетки.
Путь
в
решет-к:е
Ld
есть
последовательность
чередующихся
отличных
друг
от
друга
вершин
Xi
и ребер
li
=<
Xi-l,
Xi
>.
Такой
путь
имеет
длину
n
и
соединяет
Хо
и
Х
n
.
Путь
называетс.я
от-к:рыты.м,
если
все
его
ре
бра
открыты.
Рассмотрим
случайный
подграф
L
d
,
содер
жащий
множество
вершин
Zd
и
только
открытые
ребра.

1
'1
70
Глава
3.
Стохастические
модели
Через
С(Х)
обозначается
открытый
кластер,
содержащий
вершину
Х,
при
этом
С(Х) представляет
собой
множество
всех
вершин
решетки,
которые
связаны
с
Х
открытыми
пу
тями,
а
ребра
С(Х)
являются
открытыми
ребрами
Ld,
свя
зывающими
пары
таких
вершин.
В
силу
инвариантности
решетки
и
вероятностной
меры
по
отношению
к
переносу
вероятностные
свойства
С
(Х)
не
зависят
от
выбора
Х.
От
крытый
кластер
С
(О)
(О
-
выделенная
вершина,
называе
мая
начальной)
является,
таким
образом,
типичным
и
далее
обозначается
одной
буквой
С.
Через
С(Х)
обозначается
чи
сло
вершин
в
С(Х).
Пишут
С(Х)
=<
Х
>,
если
вершина
хне
является
инцидентным
ни
для
одного
открытого
ребра.
Значительный
интерес
в
теории
просачивания
предста
вляет
вероятность
О(р)
того,
что
заданная
вершина
при
надлежит
бесконечному
открытому
кластеру.
В
силу
ин
вариантности
решетки
и
вероятностной
меры
можно
без
ограничения
общности
считать
рассматриваемую
вершину
начальной.
Тог
да
00
О(р)
=
P(ICI
=
00)
= 1 - L
P(ICI
= n).
n=l
Легко
видеть,
что
ICI
=
00
тогда
и
только
тогда,
когда
су
ществует
бесконечная
последовательность
Хо,
XI,
Х2,
•.
• ,
от
личных
друг
от
друг
от
друга
вершин,
таких,
что
Хо
=
О,
Xi
'"
Xi+l
и
ребро
<
Xi,
ХН!
>
открыть
для
всех
i.
Ясно,
что
О
-
неубывающая
функция
от
р,
причем
0(0)
=
о
и
0(1)=1.
Фун,да.мен,та.л,ьн,ы.м
фа-кто.м
теории
nРОСа'чuван,u.я
.явм
етс.я
существован,uе
~рuтu'Ч,еС-КО20
эн,а'Ч,ен,u.я
ре
=
Pe(d)
для
р,такого,
что
Od(P)
= { =
О,
если
Р
<
Pe(d),
>
О,
если
Р
>
Pe(d);
Ре
(d)
называется
критической
вероятностью
и
формально
определяется
равенством
Pe(d)
=
sup{p
:
О(р)
=
О}.
