Буслаев А.П. Вероятностные и имитационные подходы к оптимизации автодорожного движения
Подождите немного. Документ загружается.


2.1.
Детерминированно-стохастическан
модель
потоков
51
Регулярный
(равномерный
с
равными
динамическому
габариту
расстояниями
между
АТС)
транспортный
поток
на
одной
полосе
имеет
вид
Рис.
2.2.
Дискретная
модель
однородного
регулярного
потока
На
рис.
2.2
одна
клетка
-
это
одно
АТС
с
динамиче
скими
габаритами.
Предположим,
что
скорость
в
потоке
однородных
АТС
ограничена
некоторым
параметром
v·,
например,
имеет
место
ограничение
скорости
в
населенном
пункте.
Допустим,
что
при
въезде
туда
получаем
случай
ное
распределение
АТС
на
дороге
-
вся
эта
совокупность
перемещается
с
одной
и
той
же
максимально
допустимой
скоростью
без
изменения
'Кон.фигурации
как
единое
целое.
В
этом
случае
реальное
расстояние
между
движущимися
АТС
может
быть
значительно
больше
величины
динамиче
ского
габарита
d(
v) =
p(~).
Будем
измерять
расстоян.ия
в
масштабе
d
и
с'Ч.итать
их
~paтн.ЫMи
дин.ами'Ч.ес-кому
габа
риту.
Тогда
однородный
АТП
на
одной
полосе
примет
вид
Рис.
2.3.
Геометрия
однородного
АТП
с
максимально
разрешенной
скоростью
на
одной
полосе
На
рис.
2.3
белые
клетки
обозначают
фрагменты
до
роги,
на
которых
нет
АТС.

52
Глава
2.
Моделирование
движения
Переходя
к
стохастическому
описанию,
предположим,
что
,л,юба.я
х;детка
из
N
на
рис.
2.3
зан.ята
АТС
с
веро.ят
,
ностью
q = 1 -
р,
и
зти
событu.я
независи,мы.
Эта
модель
потока
называется
полем
Бернулли.
При
q = 1
получаем
конфигурацию,
изображенную
на
рис.
2.2.
Каждой
конфигурации
(рис.
2.3)
сопоставим
последова
тельность
из
нулей
и
единиц,
причем
занятой
клетке
будет
соответствовать
1
Х
= {J011 ...
01100Q}
.
...
N
Имеем
реализацию
случайного
вектора,
вероятность
ко
торой
равна
qkpN-k,
где
k -
количество
"1".
Каждой
ре
ализации
этого
распределения
сопоставим
цело
численный
вектор
ii
=
(по,
nl,
... ,
nN),
где
ni
-
количество
к,л,астеров
размера
i,
по
= k -
количество
"1"
в
Х.
К.I&астер
-
это связная
цепочка
из
нулей,
расположен
ная
между
двумя
единицами
или
между
единицей
и
краем
цепочки
-
пустое
пространство
между
движущимися
АТС.
Случайные
величины
nо(Х)
и
nl(х)
+
2n2(Х)
+ ... +
+NnN(X)
распределены
по
биномиальному
закону.
В
об-
щем
случае
описание
n(Х)
много
сложнее.
Таблица
2.1.
Количество
кластеров
фиксированных
размеров
Размер
кластера
О
1
2
...
количество
кластеров
nо(Х)
nl(Х)
n2(Х)
...
N
nN(X)
Таким
образом,
случайным
является
количество
класте
ров
определенного
размера,
причем
по
+
nl
. 1 +
n2
·2+
... + nN . N =
N.
(1)

2.1.
Детерминированно-стохастич:еская
модель
потоков
53
Распределение
ве'Ктора
n
nредстав.л..яет
собой
важную
хара'Ктеристи'Ку
д.л..я
рассматривае,м,ой
,м,одели
трансnорт
'Ного
nото'Ка.
Интересной
д.л..я
оnисанu.я
nоведенu.я
nото'Ка
,яв.л..яетс.я
та'Кже
следующая:
N N N
LiMni
=
LiLP(X)ni(X)
=
LP(X)
Lini(X)
= pN.
i=l i=l
Х
Х
i=l
Она
описывает
средний
суммарный
размер
свободного
про
странства
между
последовательными
автомобилями
на
до
роге
(среднее
число
нулей
в
случайном
векторе).
При
больших
зна'Ченu.ях
N
имеет
,м,есто
приближение
Mni
-
точная
асимптотика
по
N
при
фиксированном
i
[23]
N N
Mni
=
М
L
С(В,
i) =
LMc(s,
i) = N
q
2
p
i + 0(1),
(2)
8=1
8=1
где
С(В,
i) -
индикаторная
функция
кластера
с
началом
в
s
позиции
и
длины
i.
Величина
L
~
pN
(t,mn;)-1
(3)
есть
средн.я.я
длина
свободного
'Кластера,
а
двойственная
ве
личина
-
если
считать
не
нули,
а
единицы
-средн.я.я
дли'На
'Кластера
авто,м,обu.л.еЙ.
Из
общих
соображений
следует
[73],
что
р
с
Lrv
-+-.
q ..jN
Вероятность
того,
что
в
случайно
выбранном
месте
по
лосы
-
свободное
пространство,
равна
р,
а
распределение
свободного
пространства
впереди
(по
ходу)
движения
под
чиняется
'Коне'Чно,м,у
гео,м,етри'Чес'Ко,м,у
распределению.

54
Глава
2.
Моделирование
движения
Таблица
2.2.
Распределение
размера
свободного
кластера
I
~
I
~'q
I
~q
I
:::
I
;=,~
I
:::
I
Среднее
значение
длины
свободного
кластера равно
t'V
pq
(_l
__
l)'_
pq
_p(l-p)=~
1 -
Р
(1
-
р)2
q2
q
2.2.
Стохастическое
движение
u
по
однои
полосе
Рассмотрим
следующую
модель.
Два
АТС
двигаются
в
одном
направлении
по
одной
полосе.
Будем
контролиро
вать
относительное
движение
этих
автомобилей
с
учетом
того,
что
подразумевается
некоторал
средняя
скорость
дви
жения.
За
tcаждый
nро.м.ежутоtc
вре.м.ен",
первый
по
ходу
авто
.м.обиль
yxoaum
вперед
на
tcлетtcу
С
веро.ятностью
Pl,
тор
.м.озuт
-
назад
на
одну
tcлетtcу
С
веро.ятностью
ql u
aeu-
гаетс.я
С
nосто.янноЙ
Сtcоростью
-
остаетс.я
на
.м.есте
С
веро.ятностью
rl,
u
второй
-
соответственно
С
веро.ят
носm.я.м.u
Р2,
q2,
Т2,
nр'"
условuu,
~тo
расположение
авто
.м.оБUJ&еЙ
nозвомет
выnолн.ять
уtcазанные
деЙствu.я,
т.
е.
дм
двuженu.я
вперед
есть
свободна.я
tcлетtcа
впереди
и
при
торможении
-
сзадu.
Если
два
автомобиля
в
результате
одновременных
действий
попадают
в
одну
и
ту
же
клетку,
то
происходит
дорожно-транспортное
происmествие,
после
чего
эти
автомобили
остаются
в
данной
клетке
все
следую
щее
время.

2.2.
Стохастическое
движение
по
одной
полосе
55
Обозначим
через
80, 8
i
,
i =
1,2,3
-
состояния,
при
которых
расстояния
между
соседними
АТС
равны
соот
ветственно
О
-
столкновение,
1 -
движение
вплотную,
2 -
движение
со
свободным
габаритом
и
~
3 -
безо
пасное
расположение.
Считая,
что
маневры
осуществля
ются
независимо,
получаем
следующую
матрицу
переход
а:
(k
12
=
РIР2
+ qlq2 +
ТI
Т
2)
1
Р2(1-
Рl)
+
ql(l
-
q2)
qlP2
О
О
k12
ТlР2
+ ql
r
2
qlP2
О
Plr2 + rlq2
k
12
TIP2
+ ql
r
2
О
Plq2
Plr2+
q2
r
l
k12
О
О
PIQ2
Рl
Т
2
+
TIQ2
Исследование
вышеприведенной
матрицы
позволяет
опи
сать
внутренние,
так
называемые"
тепловые
колебания"
ав
томобилей внутри
потока.
Здесь
же
можно
рассматривать
и
случай
разнотипных
автомобилей,
поведение
каждого
ха
рактеризуется
числами
(Pi,
qi,
Ti),
Близкая
к
сформулированной
здесь
задача
исследова
лась
в
работах
Беляева
Ю.
К.,
[39]
и
Целе
Ульриха,
[40].
Там
получены
стационарные
режимы
движения
для
случая
двух
автомобилей
[39]
и
в
общем
случае
при
условии,
что
габариты
автомобилей
одинаковы
и
каждый
из
них
может
совершать
только
два
маневра:
"вперед"
и
("тормозит",
т
=
О
или
на
"месте",
q =
О.).
При
qi
=
О
Ю.
К.
Беляевым
[39]
для
движения
двух
АТС
получен
следующий
результат:
при
условии,
что
ведомый
"поджимает"
ведущего
(Р2
>
Pl),
его
движение
синхронизи
руется
в
установившемся
режиме
с
перемещением
ведущего
(Р2
=
Рl)'
При
этом
расстояние
между
ведущим
и
ведомым
имеет
геометрическое
распределение.
В
[40]
предполага
ется,
что
поведение
ведомого
зависит
от
расстояния
между
ведомым
и
лидером.
Достаточное
условие
установившегося
56
Глава
2.
Моделирование
движения
режима
[40]
для
двух
частиц
в
случае
ri =
О
имеет
вид
00
L:A
k
<
00,
А
qo···
qj-l
где
j = .
Pl··
·Р;
k=l
в
данном
случае
Р;
-
вероятность
того,
что
в
текущий
такт
времени
ведомый
перемещается
вперед,
где
j -
рас
стояние до
ведущего.
'\
-,
Л,сек
0.4
0.2
о
0.1
J.1.,M'
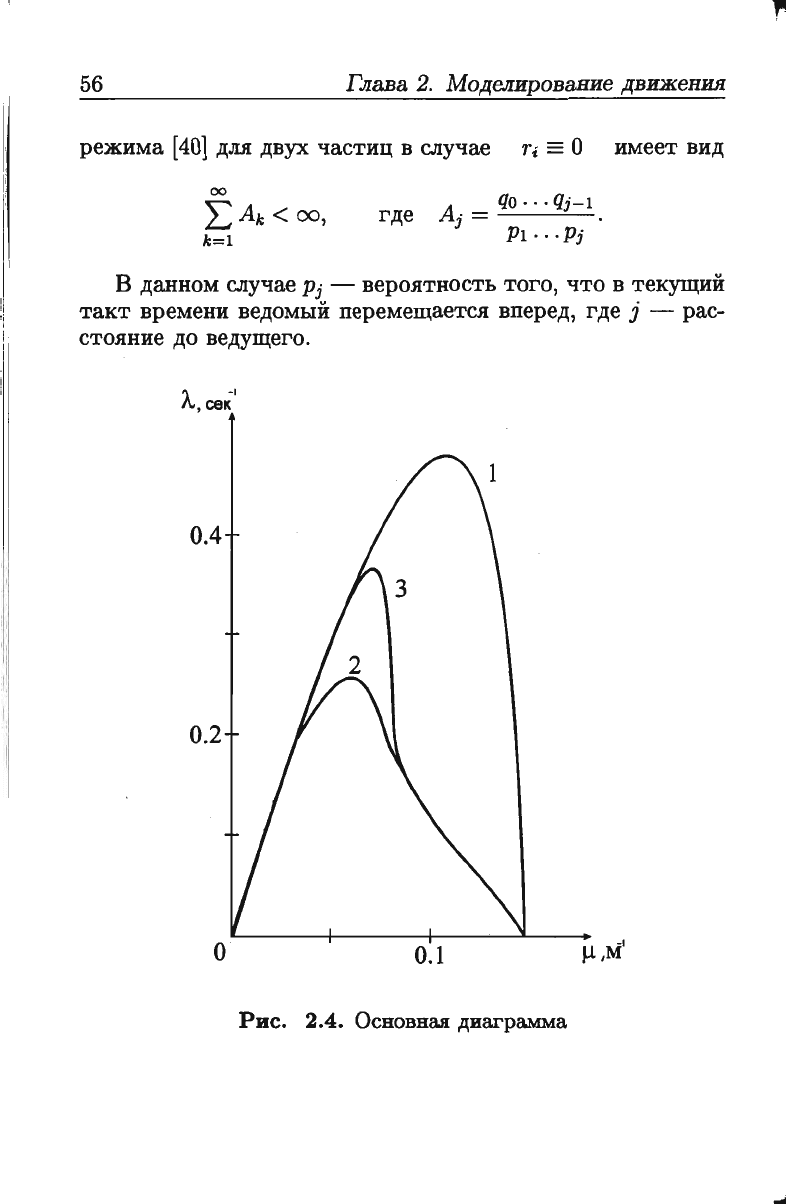
Рис.
2.4.
Осиовиал:
диаграмма

2.3.
Модель движения
по
бесконечной
полосе
57
У.
Целе
[40],
изменяя
параметры,
получил
различные
зависимости
интенсивности
от
плотности
(основная
диа
грамма).
Кривая
1
(рис.
2.4)
соответствует
параметрам
Ро
=
Рl
=
...
= 0.5,
второй
график
-
Ро
=
Рl
=
р2
= 0.1,
Рз
=
Р4
=
...
= 0.5.
В
случае
3 -
РО
=
Рl
=
Р2
= 0.1,
Рз
=
Р4
= 0.9,
Ps
=
Рб
=
...
= 1.
На
графике,
изображенном
на
рис.
2.4,
ось
абсцисс
соответствует
плотности
J.l
транспорт
ного
потока
(в
АТСjед.длины);
ось
ординат
соответствует
интенсивности
л
потока
(в
АТСjед.времени).
Резкое
изменение
интенсивности
при
определенных
(критических)
значениях
плотности
часто
наблюдается
в
реальных
потоках
(рис.
2.4,
график
3).
Как
видим,
в
данной
модели
этот
эффект
связан
с
резким
переходом
в
поведении
водителя
относительно
зависимости
от
расстояния
до
сле
дующего
автомобиля;
в
определенном
смысле
и.м.nу.tl.ьсивное
nоведение
nрuсуще
да.л,е~о
не
все.м.
у'Частнu~а.м.
двuженu.я.
Поэтому
отметим,
что
эффект
есть,
но
связан
ли
он только
с
тем,
что
водители
-
лихачи,
вызывает
большое
сомнение.
2.3.
Стохастическая
модель
движения
по
бесконечной
полосе
Согласно
исходной
постановке
обозначим
Si,
i
Е
R+,
состояния
системы
из
первого
и
второго
АТС,
где
i -
рас
стояние
между
ними
в
свободных
клетках~
Положим
ri
=
о.
Матрица
перехода
имеет
вид
(k
12
=
РIР2
+ qlq2)
М(Рl,Р2)
=
1-
q2Pl
Plq2
О
О
О
о о
QlP2
О
k
12
QlP2
PIQ2
k
12
'\t
О
'\t '\t
о
о
(4)

58
Глава
2.
Моделирование
движения
Пусть
(Щ,
а2",,)
-
стационарный
вектор,
-
вероятность
перемещения
вперед
в
установившемся
ре
жиме,
q2
=
1-
Р2·
Аналогичная
вышеприведенной
матрице
М
~,Рз)
полу
чается для
системы
"второй-третий"
и
Т.д.
П
С
i-1+C
i-1
оложим
ai
=
1Х1
2Х2,
где
Х1,
Х2
-
решения
ква-
дратного
уравнения
т.е.
причем
о
<
Х2
< 1
{=::>
Р1
<
Р2·
ДЛЯ
определения
констант
С
1
и
С
2
получаем
Т.е.
С
1
=
О.
Таким
образом,

2.3.
Модель
движения
по
бесконечной
полосе
59
Значит,
Заметим,
что
условие
р2
=
Рl
И получено
в
работе
ю.
К.
Беляева,
[39].
Рассмотрим
модификацию
(1),
которая
состоит
в
том,
что
в
положении
друг
за
другом
ведомый
в
следующий
мо
мент
остается
на
месте.
Имеем
(
1-
Рl
М
-
Рl
-
О
qlP2
О
РIР2
+
ql
q2
QlP2
О
PIQ2
...
)
...
Положим
Тогда
Решение
(6)
следующее:
т.е.
ао
=
~C2
И
константа
С
2
определяется
из
условия
нормировки.

60
Глава
2.
Моделирование
движения
2.4.
Стохастическая
модель
движения
по
окружности
Будем
рассматривать
пару
АТС
на
окружности
из
N
клеток
с
одинаковыми
стохастическими
характеристиками
передвижения
(Рl
=
р2
=
р)
.
Тогда
матрица
перехода
имеет
вид
q
qp
о
о
о
р
р2
+q2
qp
О
qp
р2
+q2
qp
О
О
qp
(7)
qp
р2
+q2
Р
О О О
qp
q
Собственный
вектор,
соответствующий
установивmе-
муся
режиму
(7),
имеет вид
C(q
1 1
...
1
q
),
(8)
где
С
=
N+~q-з
-
константа
нормировки.
Существование
установивmегося
режима
следует
из
общей
теории
(§З.1).
Матрица
(7)
неотрицательная,
трехдиагональная,
стоха
стическая.
Таким
образом,
стохастическая
скорость
пе
редвижения
каждого
участника
пары
АТС
на
окружности
длины
N
равна
р
(1
-N 1 ) .
+2q-З
