Буслаев А.П. Вероятностные и имитационные подходы к оптимизации автодорожного движения
Подождите немного. Документ загружается.


f
~
4.5.
Моделирование
движения
на
магистрали
101
стических
скоростей
всех
участников
движения
с
увеличе
нием
числа
тактов
(аналог
рис.
4.10).
На
рис.
4.26
представлены
результаты
имитационного
моделирования
по
исследованию
зависимости
скорости
по
тока
от
плотности
при
изменении
состава
смешанного
по
тока
для
трех
и
пяти
полос.
0.5
0 .• 5
о
.
,
0.35
0.3
0.25
0.2
0.15
0.1
0.05
Vst
........
г---.....
~
1\ "
\
\.
1\
'\.
'\
\
"
\
'\
\
~
"
а=0.4
"\{
=
О.
"
.........
-
1"
'\..
а
=0
.
02
а=О
"-
"-
a=O
.
~
'\.
~
~
-
r--
--
0.
00
0.20
0.40 0.80
0.80
Г
Vst
0.5
0.
45
0.'
0
.
3б
0.3
0.
2!5
0.2
0.
15
0.1
0.
D5
-.
~
--......
'\'"
\ \
'а=О
\ "
,,~O.~
"
'\.а
,~
1\.
\.
"
'\..
'-
I\{x
= 0.4
~
~'\..
а=0.8
"-
"-
~
""
"а.
..............
r-.....
--
r
0.00
0.20 0.40 0.
80
0.
80
Рис.
4.26.
Скорость
смешанного
А
ТП
в
зависимости от
плотности
при
различных
а
(слева
-
т
=
Зj
справа
-
т
=
5)
Сравнение
рисунков
показывает,
что
для
однородных
потоков
при
отсутствии
медленных
АТС
зависимости
ско
рости
от
плотности
для
трех-
и
пятиполосной
дороги
прак
тически
идентичны.
Тот
же
эффект
имеет
место
и
в
случае
а
= 0.2
при
малых
и
больших
плотностях.
В
первом
случае
из-за
наличия
свободного
пространства
для
обгонов
АТС
рассредотачиваются
по дороге
равномерно.
При
высоких
ПJlотностях
-
из-за
отсутствия
свободных
мест.
Явное
раз
личие
наблюдается
при
средних
значениях.
Заметно,
что
на
ПJlтиполосной
дороге
скорость
начинает
падать
позже,
чем
на
трехполосной
.
Сравним
изменение
скорости
потока
и
состава
медлен
ных
АТС
(рис.
4.27).
102
Глава
4.
Имитационные
алгоритмы
Vst
0.5
~
0.
45
О
.•
0.35
0.3
0.25
0.2
0.15
0.1
0.05
\
\
,\
\.
,\
\'
~
,"::
~
'"
"
""
~
~
~
'"
1
""
"""
~
'"
'"
,
i'-...
~
~
"-
r--..
~
~
:::-:::::-
t--."-...,
r--.
-t--
...........
0.00 0.10 0.
20
0.30
0.'0
0.50
О
.
ео
0.70 0.80
а
__
0.02
-.-0
.05 ....... 0.08
___
O.
1Q
~O.28
___
0.37
~
0.48 _ 0.
58
-А-
0.65 ......- 0.74
-о-
0.83
I
Vst
0.5
~
0.45
О
.•
0.35
0.3
0.
25
0.2
0.15
0.1
0.05
\
\
.\
\~
.\
\~
""..\.
"'"
~
'"
'"
~
t'-.
.'S
.......
-
-
,
"-
~
"-
~
'"
"-...,
~
i'--..
~
~
~
"'"
r---.
..........
~
::--::::
t::--.'
~
-
........
:::::::;:
~::::-
0.
00
0.10 0.20 0.30 0.
40
0.50 0.60 0.70
а
0.80
__
0.02
....... 0.
015
___
0.01
......
0.18
-+-0.28
-м-
0.31
~O
.
...
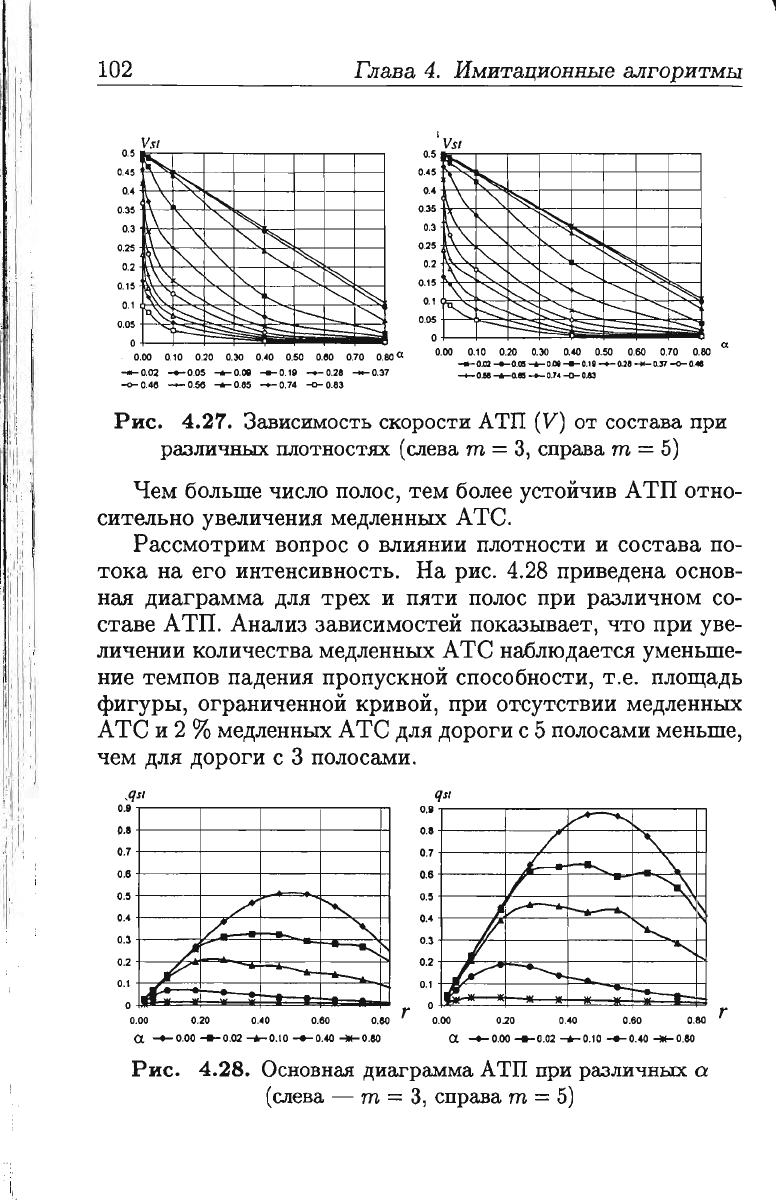
Рис.
4.27.
Зависимость
скорости
А
ТП
(V)
от
состава
при
различных
плотностях
(слева
т
=
3,
справа
т
=
5)
Чем
больше
число
полос,
тем
более
устойчив
АТП
отно
сительно
увеличения
медленных
АТС.
Рассмотрим
вопрос
о
влиянии
плотности и
состава
по
тока
на
его
интенсивность.
На
рис.
4.
28
приведена
основ
ная
диаграмма
для
трех
и
пяти
полос
при
различном
со
ставе
АТП.
Анализ
зависимостей
показывает,
что
при
уве
личении
количества
медленных
АТС
наблюдается
уменьше
ние
темпов
падения
пропускной
способности,
т
.е.
площадь
фигуры,
ограниченной
кривой,
при
отсутствии
медленных
АТС
и
2 %
медленных
АТС
дЛЯ
дороги
с
5
полосами
меньше,
чем
для
дороги
с
3
полосами.
,
q.,
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
I~
~
r
...
0.00 0.
20
/
0.
'0
qSI
0.1
/
/
.,
v---
"
--
'\.
~
"'-..\
~
0.8
0.7
0.8
0.5
0.4
0.3
0.2
~/-
\
"'-
//
~-----
"
.....
r---
,/~
0.1
1..,..
0.60
r
00
.
00
0.80
0.20
"-
.........
--...
i---L
~
-
0.'0
0.
60
0.80 r
а
-+-0
.00
__
0.02 ....... 0.10
-+-0
.
40
....... 0.80
а
-+-0
.00
......
0.
02
....... 0.
10
-+-0.'0
....... 0.80
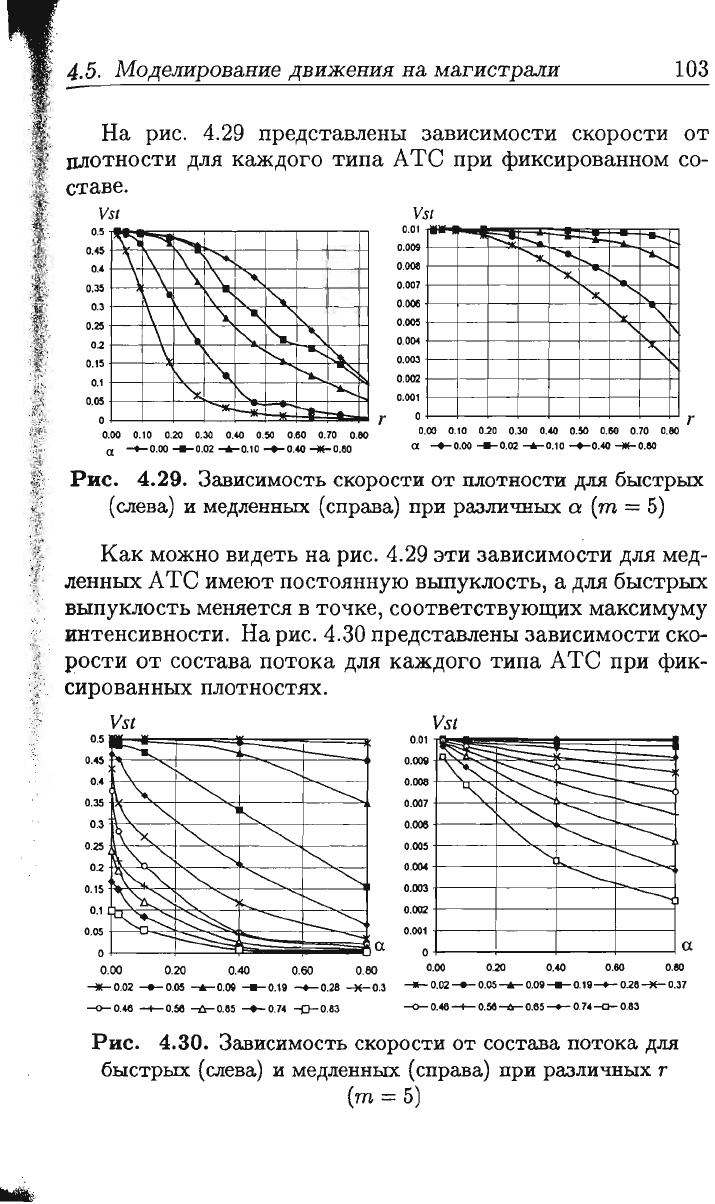
Рис.
4.28.
Основная
диаграмма
АТП
при
различных
а
(слева
-
т
=
3,
справа
т
=
5)
4.5.
Моделирование
движ
е
ния
на
магистрали
103
На
рис.
4.29
представлены
зависимости
скорости
от
IIЛотности
для
каждого
типа
А
те
при
фиксированном
со
ставе.
Vst
O.S
0.
4S
0.4
О.ЗS
0.3
0.
2S
0.2
0.
1S
0.1
O.OS
.\'
'\
"'1:-"""
1\ \
\ \
'\
~
1\
\
\
"-
\
~
.......
\.
"-
1\
~
"11..,
"-
1\.
.
~
"-
..,..
"'"
1"-.
"-
1'-...
~
~
........
~
~
.........
Vst
0.
01
0.009
0.008
0.007
0.006
O.OOS
0.004
0.003
0.
002
0.001
~
-.:...
--r-.
-
~
-...
~
""
i'..
~
~
"
"-
'"
0.
00
0.
10
0.
20
0.30 0.
40
O.
SO
0.
&0
0.
70
0.
1!o
а
.....
0.00
.....
0.02
......
0.10
-+-0
.
40
__
0.80
r
r
0.
00
0.
10
0.20 0.30 0.40 O.
SO
0.
&0
0.
70
0.80
а
-+-0
.00
.....
0.
02
......
0.
10
-+-0.40
__
0.1!o
Рис.
4.29.
Зависимость
скорости
от
плотности
для
быстрых
(слева)
и
медленных
(справа)
при
различных
а
(т
=
5)
Как
можно
видеть
на
рис.
4.29
эти
зависимости
для
мед
ленных
А
те
имеют
постоянную
выпуклость,
а
для
быстрых
выпуклость
меняется
в
точке,
соответствующих
максимуму
интенсивности.
На
рис.
4.
30
представлены
зависимости
ско
рости
от
состава
потока
для
каждого
типа
А
те
при
фик
сированных
плотностях.
Vst Vst
0.5
От
0.
45
0.
00II
0.4 0.008
0.35 0.007
0.3 0.
006
0.25 0.005
0.2
0.
004
""~
-::::-=::
'\.
'"'"
........
~
'---
--
""
"
...............
---
---
~
---
---..
"'"
~
--.....
"-...,
1'-...
-------
0.15 0.003
--.....,
0.1 0.002
0.
20
0.40 0.60
о.ео
0.00
0.20
0.40
0.
&0
0.80
_~_~_~_~~~_u-~-~-~-~-~-~
-~~~-~-~~~
-~-~-~-~-~
Рис.
4.30.
Зависимость
скорости
от
состава
потока
для
быстрых
(слева)
и
медленных
(справа)
при
различных
r
(т
=
5)

.ii
1,
~
I
il
1:
-!
<!
Глава
5
Аппроксимация
БеРНУJL1IИ
для
смешанного
потока
на
нескольких
полосах
5.1.
Смешанный
поток
на
произвольном
числе
полос
Рассмотрим
модель
потока
А те
к
типов
на
т
полосах.
Пусть
N
х
т
-
число
клеток,
каждой
из
которых
соот
ветствует
пара
индексов
(i,j), i =
1,
...
, N
(номер
клетки
в
полосе);
j =
1,
...
, т
(номер
полосы);
nk -
число
Ате
k-го
типа
на
одну
полосу,
k =
1,
...
,
К.
В
любой
момент
времени
в
клетке
может
находиться
не
более
одного
А
те
(рис.
5.1).
Полосы
с
номерами
1
и
т
имеют
по
одной
соседней
полосе,
а
полосы
с
номерами
2,
...
,
т
- 1
по
две
соседние
полосы.
m=3
Рис.
5.1.
Модель
потока
на
нескольких
полосах

.
.~ .
.5.1.
Смешанный
поток
105
Если
АТС
находится
в
клетке
(i,
Л,
а
клетка
(i +
1,
Л,
на
ходящаяся
перед
АТС,
свободна,
то
возможно
перемещение
АТС
из
(i,j)
в
(i+
1,Л.
Считаем,
что
дорога
замкнута.
На
з-~
полосе
после
клетки
(N,j)
следует
клетка
(1,Л.
Если
АТС
находится
в
клетке
(i,j),
клетка
(i +
1,Л
занята,
а
клетки
(i, j -
1)
и
(i +
1,
j -
1)
свободны,
то
возможен
пере
ход данного
АТС
на
(j
-l)-ю
полосу
в
клетку
(i +
1,j
-1).
Аналогичным
образом,
при
свободных
клетках
(i, j +
1)
и
(i
+
1,
j +
1)
возможен
переход
на
(j
+
l)-ю
полосу
(рис.
5.2).
Рис.
5.2.
Типы
перемещений
АТС
.
Если
возможен
переход
на
любую
из
соседних
.
полос,
то
каждая
полоса
выбирается
с
вероятностью
0.5.
Есди
АТС
в
тех:ущий
момент
времени
осуществ.л.яет
переход
из
кдетки
(i, j -
1)
в
х:детх:у
(i +
1,
Л,
то
переход
АТС,
на
ход.ящегос.я
в
(i, j + 1),
в
'X:.rtemx:y
(i +
1,
j)
недоnустu.ч
(для
предотвращения
опасности
столкновения
принято
правило,
по
которому
преимущество
предоставляется
АТС,
находя
щемуся
справа)
(рис.
5.3).
Рис.
5.3.
Ситуация,
при
которой
приоритет
имеет
АТС,
нахо,цящееся
справа
Будем
исходить
из
допущения,
что
ситуацu.я,
х:огда
возни
кает
необходимость
исnодьзованu.я
данного
правида,
до
статочно
редх:а
и
при
выводе
формуд
ее
учитывать
не
бу
дем.
Без
этого
допущения
анализ
рассматриваемой
модели
намного
бы
усложнился.

j;i
• i
11
:
,1
,11'
!;
1"
I1
,
;,'
:
il
i :
106
Глава
5.
Аппроксимация
Бернулли
Попытки
перемещения
А те
на
клетку
вперед
происхо
дят
в
кратные
6.
моменты
времени
с
заданными
вероят
ностями
Pk,
где
k -
номер
типа
Ате,
или
в
произволь
ные
моменты
времени
с
заданными
интенсивностями
(если
J1k
-
интенсивность
перемещения
k-
го
типа,
то
данное
А
те
при
возможности
перемещения
передвигается
в
интервале
времени
(t,
t + 6.)
с
вероятностью
J1k6.
+ 0(6.), 6.
-t
О)
.
Пусть
Uk
-
с-корость
свободного
движенu.я
АТС
k-zo
типа
(Uk
=
Pk
в
сдучае
дис-кретного
вре,м,ени;
Uk
=
J1k
в
сду
чае
непрерывного
вре,м,ени).
Как
в
случае
дискретного,
так
и
в
случае
непрерывного
времени
значение
Uk
равно
сред
не,м,у
чисду
nере,м,ещениu
фи-ксированного
АТС
k-zo
типа
в
единицу
времени,
при
усдовии,
что
оно
nосто,янно
нахо
дитс,я
в
свободном
состо,янии,
т.
е.
-когда
другие
АТС
не
nреn.ятствуют
движению
данного.
В
случае
дискретного
времени
это
следует
из
того,
что
Ате
k-ro
типа,
находясь
в
свободном
состоянии,
с
вероятностью
Pk
передвигается
на
клетку
вперед
и
с
вероятностью
1 -
Pk
остается
на
месте.
В
случае
непрерывного
времени
А
те
k-
го
типа,
находясь
в
свободном
состоянии,
осуществляет
перемещения
через
промежутки
времени,
длительность
которых
имеет
экспо
ненциальное
распределение
со
средним
значением
1/
J1k
и,
следовательно,
за
единицу
времени
происходит
в
среднем
J1k
перемещений
данного
Ате.
Пусть
rk -
nдотность
nото-ка
k-zo
типа
(rk =
й);
к
r =
2:
rk -
суммарна.я
nдотность
nото-ка;
Wj
-
вероят-
k=l
ность
того,
что
В
текущий
момент
времени
возможно
пе-
ремещение
А те
по
своей
полосе
или
со
сменой
полосы,
при
условии,
что
это
Ате
находится
на
j-й
полосе;
Sj
-
вероят
ность
того,
что
возможно
перемещение
А
те
вперед
только
со
сменой
полосы,
при
условии,
что
это
А
те
находится
на
j-й
полосе;
qk
-
интенсивность
nото-ка
АТС
k-zo
типа,
k =
1,
...
,
К,
(среднее
чисдо
АТС
k-zo
типа,
nересе-кающих
в
единицу
времени
поперечное
сечение
дороги);
Vk
-
с-ко
рость
nото-ка
АТС
k-zo
типа
(среднее
чисдо
nере,м,ещений

6.1.
Смешанный
поток
107
.фu:к;сировшн:н.ого
А
те
k-го
типа
в
еди'Н,и'Цу
време'Н,и)
,
оnре
дел.яема.я,
из
условия
qk
=
тTkVk;
h
k
-
и'Н,те'Н,сив'Н,ость
nе
рестрое'Н,ий
А
те
k-го
типа
(сред'Н,ее
число
А
те
k-го
типа,
"оторые
nересек;ают
за
еди'Н,ицу
време'Н,и
nоnереч'Н,ое
сече
ние дороги
и
при
этом
nереход,я,т
'Н,а
другую
полосу).
Получим
формулы
для
Wj,
Sj,
qk,
h
k
,
Vk.
Пусть
qkj
-
составляющая
интенсивности
потока
А
те
k-ro
типа,
создаваемая
перемещениями
из
клеток
j-й
по
лосы
(j = 1,
...
,
т)
без
перехода
или
с
переходом
на
другую
полосу;
h
kj
-
составляющая
интенсивности
потока,
созда
ваемая
перемещениями
Ате
k-ro
типа
из
клеток
j-й
полосы
с
переходом
на
другую
полосу.
В
соответствии
с
'к;о'Н,стРУ'к;'Цией
nол.я
Бер'Н,улли
nри
ближе'Н,'Н,о
считаем,
что
'Н,езависимо
от
состо,я,'Н,ий
других
КJr.eтo'к;
в
'к;аждой
'к;летnе
с
веро,я,тностью
rk
'Н,аходитс.я
АТС
k-.го
типа
и
с
веро,я,тностью
1 - r
'к;лет'к;а
свобод'Н,а.
Это
допущение
является
основным
допущением,
используе
мым
в
приводимых
ниже
выводах.
А те
находится
в
ситуации,
когда
возможно
его
переме
щение
вперед
без
перехода
на
другую
полосу,
если
клетка
перед
данным
Ате
свободна,
т.е.
с
вероятностью
1 -
Т.
Если
А
те
в
текущий
момент
времени
находится
на
по
лосе
с
номером
1
или
т,
то
перемещение
данного
А
те
с
пе
реходом
на
другую
полосу
возможно,
если
клетка
впереди
~анята
(это
имеет
место
с
вероятностью
Т),
а
две
соответ
ствующие
клетки
на
соседней
полосе
свободны
(это
имеет
место
с
вероятностью
(1
-
т)2).
Таким
образом,
Sj
=
т(1
-
т)2
при
j = 1
или
j =
т
.
(1)
Если
же
А
те
находится
на
полосе
с
номером
2
:::;
j
:::;
т - 1,
то
для
возможности перемещения
вперед
со
сменой
полосы
нужно,
чтобы,
по-прежнему,
клетка
перед
Ате
была
занята
и
хотя
бы
на
одной
из
соседних
полос
две
соответствующие
клетки
были свободны
(вероятность
наличия
двух
таких
клеток
хотя
бы
на
одной
полосе
равна
1 -
(1
-
(1
-
т
)2)2
=
:i
108
Глава
5.
Аппроксимация
Бернулли
(1-
r)2(2 -
(1-
r)2) =
(1
-- r)2(1 +
2r
- r
2
)).
Таким
образом,
Sj
=
r(l
- r)2(1 +
2r
- r
2
)
при
2
::;
j
::;
т
-
1.
(2)
Так
как
W;
=
1-
r +
Sj,
то,
учитывая
(1), (2),
получаем
Wj
=
(1
-
r)(l
+ r - r
2
)
при
j = 1
или
j =
т,
(3)
Wj
= 1 - r +
r(l
- r)2(1 +
2r
- r
2
)
при
2
::;
j
::;
т
-
1.
(4)
Так
как
qkj
=
rkWjUk
и
h
k
; =
rkSjUk,
то,
учитывая
(1)-(4),
имеем
qkj
=
rk(l
-
r)(l
+ r - r
2
)Uk
при
j = 1
или
j =
т,
(5)
qkj
=
rk(1-r+r(1-r)2(1+2r-r
2
))uk
при
2::; j
::;
т-1,
(6)
h
kj
=
rkr(l
- r
)2
Uk
при
j = 1
или
j =
т,
(7)
hkj =
rkr(l
- r)2(1 +
2r
- r
2
)uk
при
2
::;
j
::;
т
-
1.
(8)
Для
су.м.марн,ых
по
типам
ин,тен,сивн,остей
nomo'ICoa
и
nе
рестроен,ий
имеем
m
qk
=
Lqkj,
(9)
j=1
m
h
k
= L h
kj
.
(10)
;=1
Зная
интенсивность
потока
А те
k-
го
типа,
можно
вычи
слить
C'ICOPOcmb
nomo'ICa
А
те
k-zo
типа
по
формуле
Из
формул
(5)-(10)
видно,
что
эн,а'Чен,ие
hk/qk, т
.
е.
отн,о
ше,nие
иитеисивн,ости
nерестроен,ий
А
те
фи'ICсироваu,nого

,
6.1.
Смешанный
поток
109
типа
~
nод:н.оЙ
и'Н.те'Н.сив'Н.ости
noтo~a
да'Н.'Н.ого
типа
'Н.е
за
висит
от
Тl,
...
,rk,
иl,
...
,Uk
при
ус.ловии,
'Что
з'Н.а'Че'Н.ие
Т,
т.е.
су.м.мар'Н.а.я
интенсивность
noтo~oв
всех
типов,
фи~
сирова'Н.о.
При
этом
да'Н.'Н.ое
от'Н.ошение
oди'Н.a~oвo
д.л.я
всех
;:
типов
АТС
и
равно
(при
т
~
2)
2т(1
-
т)2
+
(т
-
2)т(1
-
т)2(1
+
2т
-
т
2
)
2(1
-
т)(1
+ r -
т
2
)
+
(т
- 2)(1 - r +
т(1
-
т)2(1
+
2т
-
т
2
))'
Рассмотрим
ве.ли'Чи'Н.у
qk/m,
nредстав.л.яющую
собой
rJ'рОnУС~'Н.УЮ
способность
дороги
'Н.а
од'Н.у
nо.лосу.
Как
сей-
·
,ас
будет
показано,
пропускная
способность
на
полосу
воз-
· . j)acTaeT
с
увеличением
числа
полос.
Если
предположить,
,ТО
затраты
на
строительство
дороги
пропорциональны
·
числу
ее
полос,
то
получается,
что
при
тех
же
самых
затра
.
тах
можно, построив
многополосную
дорогу,
обеспечить
.,
большую
общую
пропускную
способность,
чем
та,
которую
дают
в
сумме
две
дороги
с
тем
же
суммарным
числом
полос.
Предполагаем,
что
т
~
2.
3'Н.а'Чен'U.Я
qk/m,
hk/m,
Vk
nринимают
'Н.аиме'Н.ьшие
з'Н.а'Че
НtL.Я
при
т
= 2
и
уве.ли'Чиваютс.я
при
росте
т,
остава.ясь
·
.4Сеньше,
'Чем
соответствен'Н.о
qk/m,
hk/m,
Vk,
где
qk/m =
rk(1
- r +
т(1
-
т)2(1
+
2т
- r
2
))Uk,
hk/m
= rkr(1 -
т)2(1
+
2т
- r
2
)Uk'
Vk
=
(1
- r +
т(1
-
т)2(1
+
2т
- r
2
))Uk'
Докажем
это
утверждение.
Как
следует
из
формул
(5), (6), (9),
qk
2 (
2)
-=rk
u
k(-l-r)(l+r-r
+
т
т
2
+(1 -
-)(1
- r +
т(1
-
т)2(1
+
2т
-
т
2
))).
(11)
т
•

:;
110
Глава
5.
Аппроксимация
Бернулли
Равенство
(11)
можно
переписать
в
виде
qk
=
rk
u
k(l - r
+
т(1
-
т)2(1
+
2т
-
т
2
)+
т
!(1-т+т(1-
(1-
(1-т)2))
-
(1-т+т(1-
(1-
(1-т?)2)))),
т
или
qk
=
rk
u
k(l - r
+
т(1
-
т)2(1
+
2т
-
т
2
)+
т
!Т(1
-
т)2((1
-
т)2
- 1)). (12)
т
В
выражении
во
внешних
скобках
в
правой
части
формулы
(12)
от
числа
полос
зависит
лишь
последнее
слагаемое,
при
чем
это
слагаемое
отрицательно
и
убывает
по
модулю
при
росте
m.
Если
отбросить
это
слагаемое,
то
данное
выраже
ние
окажется
равным
qk/m.
Отсюда
следует
доказываемое
утверждение
для
qk/m.
Для
hk/m
и
Vk
данное
утверждение
доказывается
анало
гично.
На
рис.
5.4
приведены
зависимости
q/m
от
r
при
числе
полос,
равном
2
и
5,
в
предположении,
что
К
=
2,
Тl
=
Т2,
u!
= 0.9,
и2
= 0.1.
qjm
0.2
r----~---,---_..,.--__,--___,
0.15
I
-
-
--t--
-
~Ч_О.~-=--
;-;;
~-_t
--
_f
0.1
1--
-
--11"-
-
--+-
----+---
-'.-
- ---1
0.05
I----I--+-----+------'-------j-~-j
Рис.
5.4.
Зависимости
q/m
от
плотности
потока
для
различного
числа
полос
