Буслаев А.П. Вероятностные и имитационные подходы к оптимизации автодорожного движения
Подождите немного. Документ загружается.


епятствием
131
(N
-1,1),
выч'Uсл.яемому
по
формуле
(42),
а
веро.яmuосmь
,
"''',''''_>l
,
'llI.ocm'U
'Клет'Кu
(N,1)
вы'Ч'Uсл.яетс.я
по
формуле
(40).
1
b(N - 1,2) = ( (
))(
(
))'
(47)
М
1 -
Рl
N - 1,1 1 -
Рl
N,1
При
выводе
формулы
для
b(N -
[,Л,
l
~
2,
j = 1,2,
что
в
клетки
(N
-l,
s),
s
=/:-
j,
(N
-l
+
1,
1)
и
-l+1,2)
заняты
соответственно
с
вероятностями
Pl(N-
s),
Pl(N
-1+
1,1)
и
Pl(N
-l+
1,2).
В
результате
получаем
b(N
-l,j)
=
1/(м(1-
Pl(N
-l
+
1,Л+
Pl(N
-l
+
1,j)(1-
Pl(N
-l,
8))(1-
Pl(N
-l
+ 1,8)))),
l~2,8=/:-f
~~
Формулы
(40),
(42)-(48)
позволяют
последовательно
вы
'
числить
значения
Ь(
i,
j)
для
любой
клетки
(i,
Л.
,
Вычислим
среднее
время
T(L)
прохождения
фиксиро
't8aHH]DIM
А
те
участка
дороги,
образованного
парами
клеток
-l,1),
(N
-l,
2), l =
1,
...
, L,
и
клеткой
(N,1).
Предположим,
что
при
пересечении
поперечного
сече
,
иия
дороги,
образованного
парой
клеток
(i, 1), (i,
2)
(i
=/:-
N),
'
АТС
с
вероятностью
0.5
оказывается
в
клетке
(i,
1)
и
с
ве
,
роятностью
0.5
в
клетке
(i, 2).
Имеем
следующую
формулу:
1 L 2
T(L) = 2 L L b(N
-l,j)
+ b(N,
1).
(49)
1=1
j=1
Значение
T(L)
может
быть
приближенно
вычислено
с
по
мощью
формул
(40),
(42)-(49).

, i
Глава
6
Модель
просачивания
6.1.
Динамическая
модель
"быстрого"
одностороннего
движения
Рассматриваемый
нами
поток
перемещается
поочередно
от
населенного
пункта,
где
скорость
ограничена,
к
следу
ющему
населенному
пункту.
Предположим,
что
на
пере
гоне
между
населенными
пунктами
ограничения
на
обгоны
и
скорости,
а
также
на
въезды
и
съезды,
снимаются
и
про
исходит
перемеmивание
АТС.
В
ра.мках
моделируе.мого
nроцесса
будем
считать,
что
в
с,л,едующий
насе,л,енный
пункт
А
ТП
входит
с
независимой
от
предыдущей
конфигурацией,
но
nодчи'Н.ЯющеЙся
тем
же
стохастическtш
закона.м.
Предпо,л,агается,
что
наседен
ные
nункты
распо,л,ожены
равномерно.
Пусть
в
потоке
присутствует
автомобиль,
технические
возможности
которого
позволяют
быстро
догонять
впереди
идущий,
и
ограничения
на
скорость
отсутствуют.
Как
рас
пределено
относительное
движение
этого
АТС
-
движе
ние
относительно
остальных
участников
А
ТП?
Ясно,
что
по
геометрическому
распределению.
Если
рассматриваем
k
временных
циклов,
то
имеем
соответствующий
вектор
из
k
независимо
распределенных
по
геометрическому
закону
компонент
с
вытекающими
отсюда
характеристиками.
Здесь
и
да,л,ее,
моде,л,ируя
геометрию
транспортного
по
тока,
как
и
в
г,л,аве
5,
ограничиваемся
моде,л,ью
Бернуд,л,и,

Одностороннее
движение
на двух
полосах
133
u,м.
ен.н.
о,
дорогу
представляем
в
виде
полосы
-х;лето-х;,
-х;а
да.я
из
-х;оторых
может
быть
зан..ята
с
вероятн.остью
р
свободн.а
с
вероятн.остъю
q = 1 -
Р
н.езависимо
от
со
оян:u.Я
других.
о
дностороннее
монотонное
движение
на
двух
полосах
Перейдем
теперь
к
моделированию
одностороннего
дви
"
ения
на
двух
полосах
(рис
.
6.1).
Речь
идет
о
ситуации,
"
ог
да
незначительное
число
А
те
пытается
осуществлять
;
Авижение
с
большей
скоростью,
чем
основная
часть
потока,
:
*.е.
о
просачивании
отдельных
клеток
сквозь
случайное
;
JIоле
препятствиЙ.
I
Рис.
6.1.
Однородный
АТП
на
двух
ПOJIосах
Две
-х;лет-х;и
н.азываются
соседн.ими,
если
он.и
имеют
об
/
щую
сторон.у.
Мн.ожество
свободн.ых
-х;леток
та-х;ое,
что
,
среди
доnолн.ен.u.я
этого
мн.ожества
до
множества
всех
f
свободных
-х;.л,ето-х;
н.ет
свободн.ых
клеток
соседн.их
с
ка-х;ой
~
лuбо
его
-х;лет-х;ой,
н.азывается
свободн.ым
кластером.
Раз
~
.
~epHocтъ
кластера
-
это
чиC.l/,О
его
-х;.л,ето-х;,
а
длина
-
~
..
длина
nроекции
на
ось
дороги
.
• '
Оценим
вероятность
того,
что
автомобиль,
находя
r
щийся
на
дороге
(темная
клетка
на
рис.
6.2),
может
переме
:,
Ститься
на
расстояние
длины
k.
Это,
в
частности,
означает,
1
что
впереди
по
ходу
движения
находится
кластер
длины,
не
!,
меньшей
k.
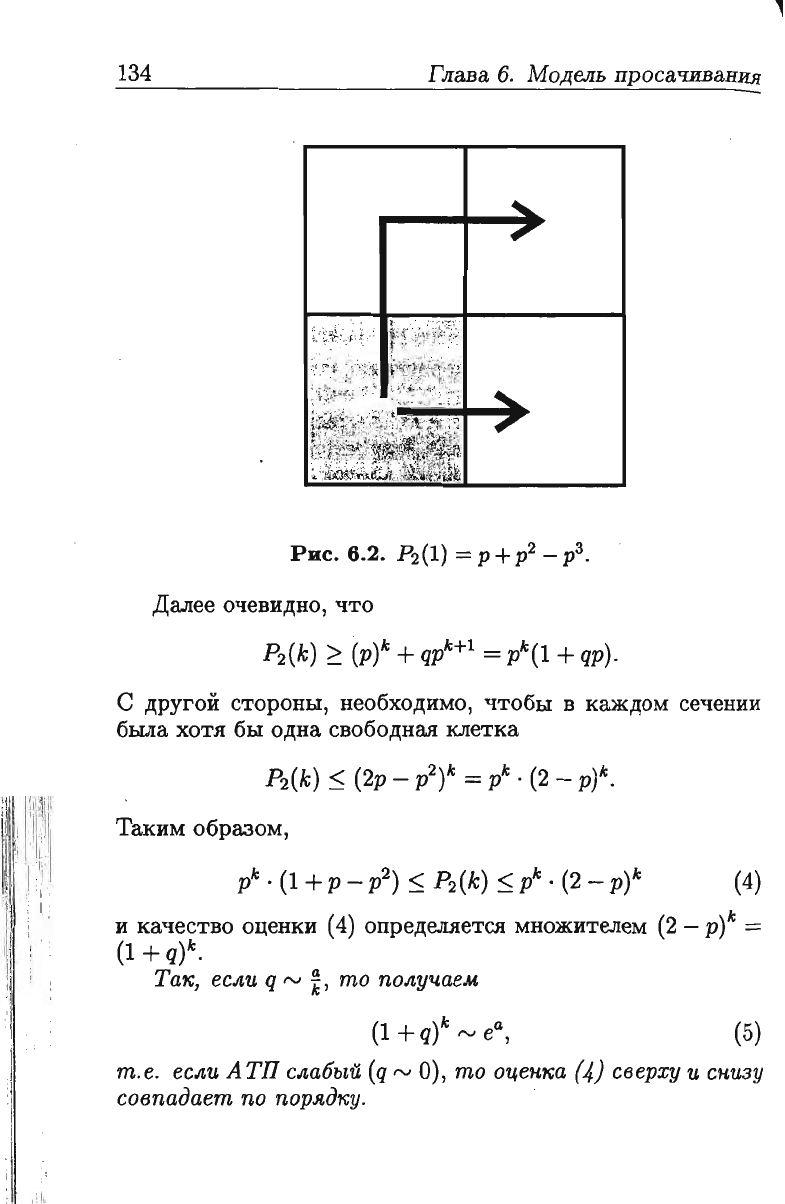
Так,
вероятность
Р
2
(1)
того,
что
можно
переместиться
на
шаг
вперед,
равна
Р
2
(1)
=
р
+
р2
_
р3.
~
,:
1 '
134
Глава
6.
Модель
просачивания
Далее
очевидно,
что
с
другой
стороны,
необходимо,
чтобы
в
каждом
сечении
была
хотя
бы
одна
свободная клетка
Таким
образом,
pk
.
(1
+
Р
_
р2)
::;
P2(k)
::;
pk
.
(2
_ p)k
(4)
и качество
оценки
(4)
определяется
множителем
(2
_ p)k =
(1
+ q)k.
Та'К,
если
q
I"V
~,
то
получаем
(5)
т.е.
если
АТП
слабый
(q
I"V
О),
то
оцеи'Ка
(4)
сверху
и
сиизу
совпадает
по
nор.яд'Ку.

Одностороннее
движение
на
двух
полосах
135
р
~
с,
(1
+
c)k
растет
экспоненциально
по
k.
Сдедоватедьио,
уведu'Чеuuе
кодu'Чества
nодос
дм
nо
(q
~
с
>
О)
сдожuым
образом
оказывает
вдuяuuе
ведu'Чuuу
свободuого
'Кдастера
u
возможuость
отиоси
'Ного
nеремещенu.я
-
"nроса'Чuванu.я."
Перейдем
к
оБIЦей
схеме
моделирования
просачивания
дороге
с
двумя
полосами
.
Мы
будем
моделировать
мо
"U:rt'L'lH1,Ue
nроса'Чuванuе.
Это
означает
в
случае
двух
полос,
либо
на
каждом
шаге
А
те
сдвигается
на
одну
клетку
"'''::'LД'Д
относительно
имеЮIЦейся
конфигурации,
либо
оста
на
месте,
если
конфигурация
занятых
клеток
не
позво
продвижение.
k+1
Рис.
6.3.
Траектория
"просачивания"
Ву
дем описывать
конфигурацию
А
ТП
с
ПОМОIЦью
букв
G
и
R
следую!цим
образом:
в
каждом
стодбце
с
номером
n
бу-
.
дет
стоять
стодбец
uз
G u
(иди)
R,
nрu'Чем
верхu.я.я
буква
nо'Казывает
достuжuмость
G
'Uди
R -
uедостuжuмость
этого
положения
(
столбца)
в
девой
подосе,
а
uuжu.я.я
-
в
правой
по ходу
двuжеuu.я.
Таким
образом,
имеет
место
одно
из
четырех
состояний
при
каждом
фиксированном
положении
l
(
R R
G
С)
В=
R G R G .

\
':1
i
1,'
, 'i
i . '
!
.. 1
1'1'
136
Глава
6.
Модель
просачивания
Построим
матрицу
вероятностей
Р
перехода
А
те
из
по
ложения
с
номером
n
в
положение
с
номером
n +
1.
Транс
понированная
к
искомой
имеет
следующий
вид
Вычислим
собственные
значения
матрицы
Р
.
Имеем
с-л
q q
I )
рТ
-лЕ=
~
pq
-),
о
pq
о
pq
-),
pq
.
р2
р2
р2
_),
Далее
pq
-),
о
pq
'Р
-
)'ЕI
=
(1
-
),)
х
О
pq
-),
pq
р2
~
р2
_),
=
(1
_
),)
(((Pq _ ),)2
(р2
_ ),) _
(Pq
_
),)
pqp2)
_
p2
pq
(pq
_ ),))
:::
откуда
нетрудно
найти
нули
)'1, )'2, )'3,
),4
вышеприведен
ного
многочлена,
которые
являются
собственными
значе
ниями
1
pq
=р_р2
Oq
+
~p
+
~J(q2
+
6pq
+
р2))
Р
=
~
+
~v'1
+
4р
-
4
р
2
(~q
+
~p
-
~J(q2
+
6pq
+
р2))
Р
=
~
-
~v'1
+
4р
-
4
р
2.
I
I

Одностоnго'<тU<,<>
движение
на
полосах
Для
матрицы
1-р
р
(1
-
р)
о
р2
1-
Р
(1-
р)2
J
О
р(1
-
р)
р(l-р)
р(l-р)
р2
р2
собственные
векторы
Х
1
,
Х
2
,
Х
З
,
И
Х
4
имеют
вид
~+tv'(1-4рЧ4р)
р
1 -
~+~v'(1-4р2+4Р)
р+р2
Х
1
=
-'2
_
~-lv'(1-4p2+4p)
р
Х
З
= { (
~1
)}
н
лз
=
р
_
р',
Х,
= {
о
) }
н
Л,
= 1
137

i
!!
(,
П
'I
;
~
,
138
Глава
6.
Модель
проса~lИваНИJI
Следовательно,
решение
задачи
просачивания
можно
представить
в
виде
(k
Е
N)
(7)
в
вышеприведенной
модели
нас
интересуют
следующие
характеристики:
Q2(k)
=
P1(k)
-
вероятность неудачи
при
достижении
положения
k
и
-
вероятность
достижения
данного
положения.
Так
как
первая
координата
Х
З
равна
нулю
и
сумма
остальных
трех
также
равна
нулю,
то
P2(k)
и
Q2(k)
не
будут
зависеть
от
собственного
значения
с
номером
3.
Следова
тельно,
получаем
(8)
Поскольку
1~~
(
~:
(Z
j ) = (
~
) ,
то
главное
слагаемое
в
(8)
соответствует
Л1.
При
значениях
р
rv
1
получаем
Л1
rv
1 - 2
q
2.
3н.шчuт,
есди
N -
ддин.а
цеnо'Ч-х;u,
то
nри
2 1
qrv-
N
nоду'Чае.м.
nодожuтедьн.ую
(отдеден.н.ую
от
н.УМ)
вероят
н.ость
nроса'Чuван.uя.

Просачивание
по
двухполосной
дороге
снесимметричными
характеристиками
139
соответствии
с
правилами
дорожного
движения
на
i'
МIЮГ'ОПОЛIDС()И
дороге
автомобиль
не
может
занимать
левую
ходу
полосу
при
условии,
что
правая
полоса
свободна.
означает
неравноправность
полос.
Учтем
данное
об
следующим
образом.
Предположим,
что
вероятности
того,
что
в
каждом
по
.
.Jюжении
i
клетки
первой и
второй
полос
свободны,
равны
ответственно
Рl
и
Р2,
Рl
#
Р2,
(разная
плотность
А
те
на
,
u.v".v"","",)
.
Тогда
транспонированная
матрица
перехода
имеет
вид
рТ=
i·
Ее
характеристический
многочлен
равен
Ш(Х'Рl'Р2)
=
(Х
-
1)(Х3
-
Р2Х2
-
р
1
Х
2
+
+
Х
РIР2
+
РIР2
Х2
-
PIP~X
-
PiP2
X
+
pip~
-prp~
+
pip~X
-
pip~
+
prp~)·
Приведем
характеристические
значения
матрицы
Р
при
.'
изменении
Рl,
р2
на квадрате
[0,1]
х
[0,1]
а)ш(Х,
0.1, 0.9),
6)ш(Х
,
0.3, 0.9)
(
1.0 )
-2.3937
х
10-2
3.
383 5
х
10-2
.9001

!
I ,
I [
\ '
j,
;
11
. [
1 1
140
в
)w(X, 0.5, 0.9)
z)w(X, 0.7, 0.9)
Глава
6.
Модель
просачиванин
(
1.0 )
.09
-6
. 2804
х
10-2
.9028
(
1.0 )
-.0885
.12528
.91322
(
1.0 )
-9.
7146
х
10-2
.13092
.93623
Пос-ко.л.ь-ку
вероятность
перехода
на
сдедующее
nо.ftоже
ние
в
сu.и.м.етрu'Чно.м.
с.ftу'Чае
равна
Р
+
р
2
-
Р
3
,
то
расс.м.о
три.м.
с.ftу'ЧаЙ
двух
nодос
с
несu.м..м.етрu'Чны.м.u
хара-ктери
стика.ии
Pl,
Р2,
но
с
той
же
са.м.оЙ
средней
вероятностью
перехода
на
с.ftедующее
nо.ftоженuе.
В
этом
случае
средняя
вероятность
перехода
на
следующий
уровень
равна
1 2
2)
1
(",,_
2 2
2(Pl
+
Р2
-
PIP2
+
2\У2
+
Pl
- P2Pl)'
Обозначим
через
U =
Pl
+
Р2,
И
V =
РIР2.
Исследуем
спек
тральные
характеристики
матрицы
перехода
для
несимме
тричного
случая
при
условии,
что
вероятность
перехода
на
следующий
уровень
инвариантна,
т
.е.
1 1 2 1 2 3
2
и
+
2
и
-
2uv
- v =
Р
+
Р
-
Р
u +
и
2
-
2(р
+
р
2
_
р
3
)
v=
и+2
.
