Буслаев А.П. Вероятностные и имитационные подходы к оптимизации автодорожного движения
Подождите немного. Документ загружается.


8.5.
Сеть
дорог
с
нерегулируемыми
перекрестками
231
где
r(c,k)
R(c,
k,
8)
=
(1
_ r(v,
8))1+1'
V
=1=
с.
Считаем,
что
R(c,
k,
8)
< 1
(иначе
образуются
заторы).
Далее,
используя
подход,
описанный
в
§8.4,
можно
вычи
слить
вторую
итерацию
Й(
с,
k,
s)
плотности
потока
на
рас
сматриваемой
полосе
k-й
дороги
с-й
полосы
с
учетом
воз
можности
наличия
в
сети
очередей,
средняя
длина
которых
не
меньше
расстояний
между
перед
перекрестками.
Для
устойчивости
потоков
нужно,
чтобы
выполнялось
неравенство
Й(с,
k,
8)
<
1.
Предполагая,
что
интенсивность
noтo~a
на
расс.ма
тривае.моЙ
подосе
по-прежнему
nрuбдuженно
оnредем
етс.я
по
фор.муде
(3)
и
учитывая
формулу
(5),
а
также
фор
мулу
Поллачека-Хинчина,
получаем,
что
среднее
время
пребывания
АТС
в
очереди
перед
соответствующим
пере
крестком
вычисляется
по
формуле
Т
( k ) _ R
2
(с,
k,
8)
с,
,8
-
р(1
_ R(c,
k,
8))Т(С,
k)(1
-
т(с,
k))'
(6)
Т(с,
k)
=
LT(c,
k,
8).
(7)
Сделаем
допущение,
что
среднее
вре.м.я
V
(с,
k)
nрохо
жденu.я
подосы
k-iJ.
дороги
с-й
группы
nревышает
веди
'Ч'ttff.у
U(k, s),
вы'Чuсме.мую
по
формуде
(1),
на
ведu'Чuну
Т(с,
k, -
Т*(с,
k).
Таким
образом,
получаем
следующую
формулу:
V(c,
k)
=
U(с,
k)
+
Т(с,
k)
-
Т*(с,
k),
(8)
где
U(с,
k)
вычисляется
по
формуле
(1),
Т*(с,
k)
по
формуле
(4)
и
Т(с,
k)
по
формулам
(6), (7).

232
Глава
8.
Движение
на
перекрестка,х
8.6.
Математическая
модель
АТП
на
регулируемом
перекрестке
двух
дорог
Пусть
замкнутая
однополосная
дорога
описывается
по
следовательностью
клеток
{1}, {2},
...
, {N}.
Клетка
{1}
следует
за
клеткой
{N}.
Будем
считать,
что
клетка
со
ответствует
месту
въезда
на
регулируемый
перекресток.
Пусть
в
течение
f
тактов
времени
разрешен
переход
А
те
из
клетки
{N
- 1}
в
клетку
{N}
и
в
течение
последующих
9
тактов
времени
такой
переход
запрещен
(рис.
8.13).
На
полосе
дороги
находится
т
АТС.
Пусть
r =
т;..
ФАЗА
ЗЕЛЕНОГО
СВЕТА
для
ПЕРВОЙ
ДОРОГИ
ФАЗА
ЗЕЛЕНОГО
СВЕТА
для
ВТОРОЙ
ДОРОГИ
Рис.
8.13.Модель
регулируемого
перекрестка
Будем
вычислять
очередь
перед
перекрестком
способом,
аналогичным
использовавшемуся
в
§8.2,
но
будем
исполь
зуем
теперь
формулу
для
средней
длины
очереди
в
системе
массового
обслуживания
сненадежным
прибором,
т
.е.
с
прибором,
который
попеременно
находится
в
фазах
рабо
тоспособности
и
отказа.
Пусть
одноканальная
система
массового
обслуживания
с
пуассоновским
входящим
потоком
с
интенсивностью
q,
экспоненциальным
распределением
времени
обслуживания,

Движение
на
регулируемом
пеDеjl\:Dlес']мке
233
загрузкой,
равной
т,
имеет
чередующиеся
фазы
пребыва
.
иия
обслуживающего
прибора
в
работоспособном
состоя
иии
(nредnо.лагае,м"
'Что
эта
фаза
и,м,еет
Э1\:сnон.ен.'Цuа.льн.ое
расnреде.лен.ие
со
cpeдн.u.м
зн.а'Чен.ие,м,
J)
и
пребывания
при
бора
в
состоянии
отказа
постоянной
длительностью,
рав
иой
g.
Средняя
длина
очереди
в
этой
системе
вычисляется
по
формуле,
выводимой
известными
методами
теории
мас-
•
сового
обслуживания
[36],
n=
~
2
2(/+9)
+ r
1
~
Ш
r
.
f
(1)
Длительность
фазы
зеленого
света
постоянна,
а
не
имеет
экспоненциальное
распределение,
но
для
средней
длины
очереди
в
системе
массового
обслуживания
с
нена
дежным
прибором,
в
которой
фазы
работоспособности
и
отказа
постоянны,
отсутствует
удобное
аналитическое
вы
ражение.
Подставляя
в
формулу
,
(1)
значение
q,
равное
т(1
-
т)р,
получаем
следующую
формулу
для
средней
длины
очереди
перед
перекрестком
(2)
Формула
(2)
выполняется
в
случае
выполнения
условия
устойчивости
потока
f
r < f + g.
Если
r
~
ftg,
то на
дороге
возникает
затор.
234
Глава
8.
Движение
на
перекрестках
8.7.
Математическая
модель
АТП
на
u
прямоугольнои
сети
дорог
с
регулируемыми
перекрестками
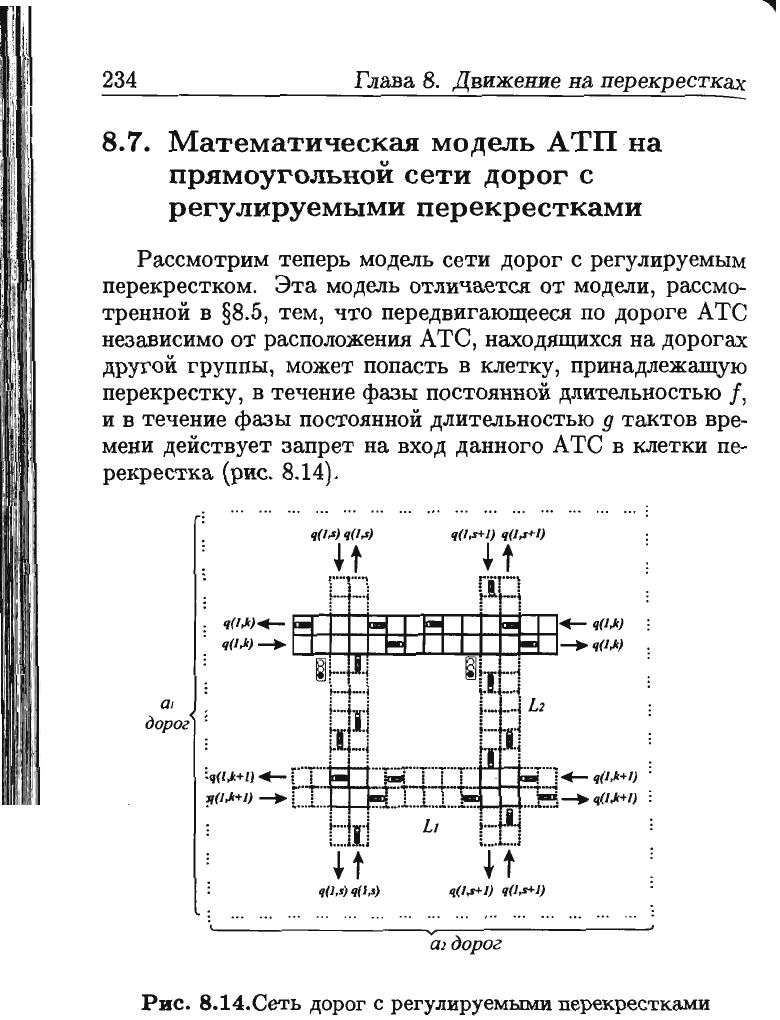
Рассмотрим
теперь
модель
сети
дорог
с
регулируемым
перекрестком.
Эта
модель
отличается
от
модели, рассмо
тренной
в
§8.5,
тем,
что
передвигающееся
по
дороге
АТС
независимо
от
расположения
АТС,
находящихся
на
дорогах
другой
группы,
может
попасть
в
клетку,
принадлежащую
перекрестку,
в
течение
фазы
постоянной длительностью
J,
и
в
течение
фазы
постоянной
длительностью
9
тактов
вре
мени
действует
запрет
на
вход
данного
АТС
в
клетки
пе
рекрестка
(рис.
8.14).
OJ
дорог
q(I,s) q(1,s)
q(1,S+1) q(1,S+1)
.t
.t
:;Z~H
11
fU
н
11
m
I~=;Z
~
i····t···j
~
i·(f····j
'····'····1
,
..•....
,
. . . . I .
i
....
i·l·i 1
.........
1
L2
: I : : i :
:
I"[t·
'1
""Ч'1
:
;",
...
"
+-ггн-wттыrr
.~,+-
,,'Щ'
'
lI(I,k+l) ..........
Г··Т··
-°"t···r-r"-r"-:···
...
~
......
q(l,k+J) :
.
..
..
_
...
!····!I·!
...
_
...
_
...
~.;_
...
_
...
!
....
i.i.!
...
_....
:
t
...
.1.
J i
...
.l
...
J
.t .t
ч(1,.) ч(1,.)
q(I,S+1) q(I,S+1)
а2дорог
Рис.
8.14.Сеть
дорог
с
регулируемыми
перекрестками

8.7.
Сеть
дорог
с
регулируемыми
перекрестками
235
Для
среднего
времени,
за
которое
АТС
проходит
k-ю
дорогу
с-й
группы,
можно
использовать
формулу
(8)
§8.5,
причем
U(с,
k)
вычисляется
по
формуле
(1)
§8.5,
Т*(с,
k)
по-прежнему
вычисляется
по
формуле
(4)
§8.5,
Т(с,
k)
вы
числяется
по
формуле
(7)
§8.5,
а
Т(
с,
k,
В)
не
зависит
от
s
и
определяется
формулой
Т(с,
k,
В)
=
-
рт(с,
k)(1
-
т(с,
k))(1 -
о/т(с,
k))·
9
2r
{1-r)p
+
т
2
(с
k)
2(1+9) ,
(1)
Формула
(1)
выводится
аналогично
формуле
(6)
§8.5
с
учетом
формулы
(1)
§8.6
для
средней
длины
очереди
в
си
стеме
массового
обслуживания
сненадежным
прибором.
Формула
(1)
используется
в
~учае
выполнения
условия
устойчивости
потока
/
т(с,
k)
<
-/-.
+g
Если
имеет
место
неравенство
/
Т(
с,
k)
~
/ +
g'
то
на
k-й
дороге
с-й
группы
возникает
затор.

11
I
1 1
236
Глава
8.
Движение
на
перекрестках
8.8.
Численное
исследование
модели
АТП
по
однополосному
мосту
на
дороге
с
двухсторонним
движением
в
данном
параграфе
приведены
результаты
вычислений,
проведенных
по
полученным
в
[64]
формулам
для
среднего
времени
ожидания
в
математической
модели
движения
ав
томобилей,
пересекающих
однополосный
мост
на
дороге
с
двухсторонним
движением.
Проведен
анализ
результатов
вычислений.
В
модели,
рассматривавшейся
в
[64],
движение
по
мо
сту
осуществляется
попеременно
в
двух
противоположных
направлениях
(рис.
8.15).
Как
только
автомобиль
начнет
двигаться
по
мосту
в
некотором
направлении,
автомобили,
движущиеся
в
противоположном
направлении,
должны
ожи
дать,
образуя
очередь.
Автомобиль
относится
к
первому
или
второму
типу
в
зависимости
от
того,
в
каком
напра
влении
он
движется.
Поступающие
в
очередь
автомобили
i-ro
типа
i = 1,2,
образуют
пуассоновский
поток
с
ин
тенсивностью
Лi.
Интервал
времени,
в
течение
которого
движутся
автомобили
типа
i,
называется
периодом
типа
i.
Как
только
период
типа
i
заканчивается,
начинается
пе
риод
типа
j.
Каждому
автомобилю
из
очереди
требуется
начальная
задержка
в
'г
секунд,
т.е.
требуется
kT
.
секунд
для
того,
чтобы
автомобиль,
занимавший
в
начале
пери
ода
данного
типа
k-e
место
очереди,
начал
пересечение
мо
ста.
Длительность
пересечения
автомобилем
моста
равна
постоянной
величине
Т
секунд.
Автомобиль
типа
i,
при
бывший
в
момент
времени,
когда
очередь
автомобилей
i-ro
типа
пуста,
но
на
мосту
еще
находятся
автомобили
типа
i,
начинает,
не
останавливаясь,
двигаться
по
мосту.
,-------'/
~-)
----------
~
~
c::fr
c::fr
c::fr
/
Мост
',-_А_
1
___
_
Рис.
8.15.Модель
моста,
рассматриваемая
в
[64]

. 8.8.
Движение
по
мосту
237
Отметим,
что
в
реальной
ситуации
при
движении
по
однополосному
участку
на
дороге
с
двухсторонним
движе
нием
обычно
либо
устанавливается
светофор,
попеременно
обеспечивающий
преимущество
автомобилям,
движущимся
в
том
или
ином
направлении,
либо
автомобили,
движущи
.
еся
в
одном
из
направлений,
постоянно
имеют
преимуще
ство,
что
обеспечивается
посредством
установки
дорож
ного
знака
(рис.
8.16).
+CJ
+CJ
('
...
'
)+
(-)+
+CJ
----------~-----i
..
~-----------
(_~
~
_
(1_)+
Рис.
8.16.
Мост
с
приоритетом
для
одного
из
направлений
движения
Эта
модель
может
также
интерпретироваться
как
мо
дель
перекрестка
со
специальным
правилом
управления
движением
автомобилей
(рис.
8.3, 8.17).
Рис.
8.17.
Другая
интерпретация
модели,
рассматривавшейся
в
[64]

, 1,
1
",1
1
:!
1:
2З8
Глава
8.
Движение
на
перекрестка:х
Как
показано
в
[64],
необходимым
и
достаточным
усло
вием
того,
что
среднее
число
автомобилей
в
каждой
из
оче
редей
Ql
и
Q2
имеет
конечное
значение,
является
неравен
ство
лIт
+
Л2Т
<
1.
Приведем
значения
средней
длины
очереди
n
на каж
дом
направлении,
которые
вычисляются
с
помощью
фор
мулы
(4) §8.1,
полученной
в
[64],
и
формулы
Литтла
n =
лw
(n
-
средняя
длина
очереди;
л
-
интенсивность
потока;
w -
среднее
время
ожидания)
при
т
=
Т
=
1,
Л1
=
Л2
=
л.
Значения
n
сравниваются
со
значениями
n*
средней
длины
очереди
перед
прекрестком
на
второстепенной
дороге,
вы
численными
с
помощью формулы
(8) §8.2.
в
этих
вычислениях
в
формуле
(8) §8.2
полагалось:
-
rl
=
Т2
= r =
лт
=
лТ
=
л
(при
этом
условии
крити
ческое
значение
л,
равное
~,
соответствует
равной
1
сумме
плотностей
Т1
и
Т2
потоков
на
двух
дорогах
в
модели,
рас
сматриваемой
в
§8.2;
другими
словами,
если
данное
усло
вие
выполняется,
то
в
модели
[64]
отношение
значения
).
к
критическому
значению
равно
значению
rl
+
Т2
в
модели,
исследуемой
в
§8.2);
- l = 1
(зона
внимания
состоит
из
одной
клетки).
Результаты
вычислений
приводятся
в
таблице
8.З.
Таблица
8.3.
Результаты
сравнения
значений
средней
длины
очереди,
вычисленных
по
формуле
[64]
(n)
и
по
формуле
из
§8.2
(n*);
т
=
Т
= 1
л
(Т)
0.1 0.2 0.3 0.35
n 0.06
0.16 0.42
0.72
n*
0.02 0.14 0.96 3.97

8.9.
Модель
с
учетом
потоков
ой
скорости
239
в
рассматриваемом
случае
для
модели
[64]
критическое
значение
л равно
0.5,
а
для
модели,
рассматриваемой
в
§8.2,
критическое
значение
л
= r
удовлетворяет
уравнению
r =
(1
-
т)2
и
приблизительно
равно
0.4.
Соответственно
при
прибли
жении
л к
0.4
значение
n·
начинает
значительно
превосхо
дить
n.
Отметим,
что
если
в
формуле
(8)
§8.2
положить
l =
О,
то
условием
стационарности
будет
иметь
вид
Т.е.
при
Тl
=
Т2
= r
критическое
значение
r
будет
равно
0.5,
что
аналогично
ситуации,
имеющей
место
в
модели
[64],
где
в
рассматриваемом
случае
(лl
=
Л2
=
Л,
r =
1)
критическое
значение
л
равно
0.5.
8.9.
Математическая
модель
АТП
на
простом
перекрестке
с
u
учетом
потоковои
скорости
в
данном
параграфе
рассматривается
обобщение
ма
тематической
модели
простого
пересечения
двух
однопо
лосных
дорог
С
односторонним
движением,
рассматривав
mейся
в
§8.2.
В
зтом
обобщении
движение
представляется
как
сумма
стохастической
и
детерминированной
составля
ющей
(nотох:овой
сх:орости)
,
что
более
адекватно
отра
жает
реальный
процесс
движения
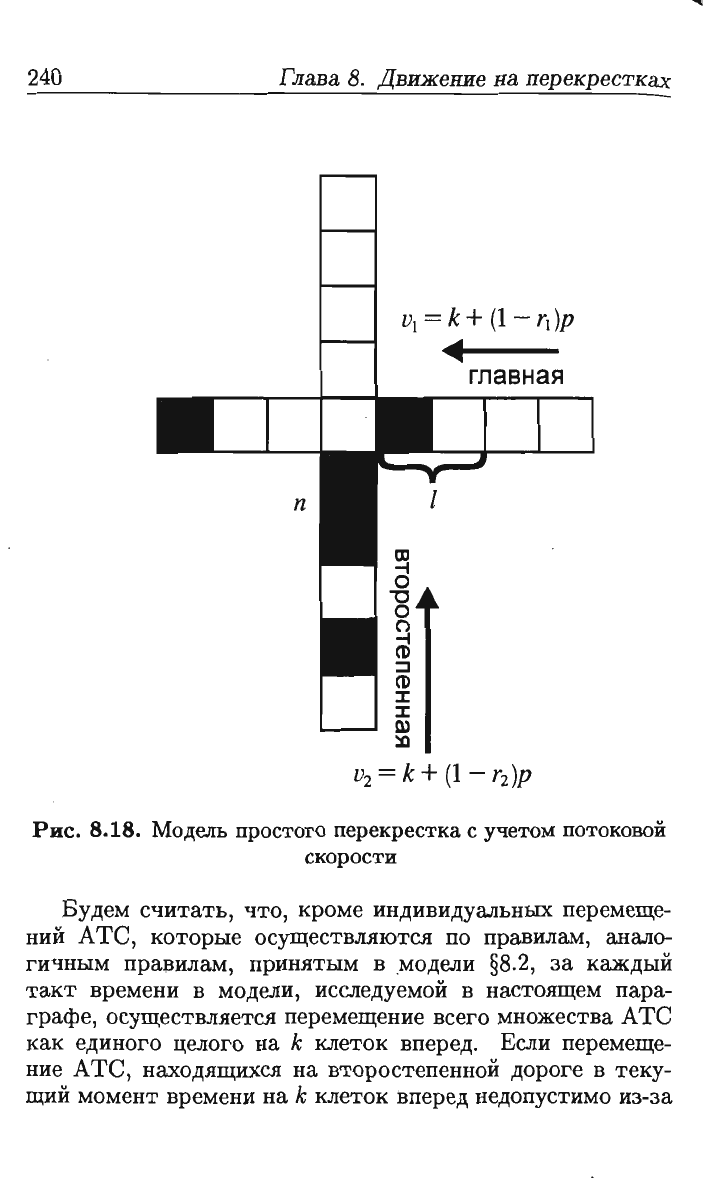
(рис.
8.18).
240
Глава
8.
Движение
на
перекрестках
главная
Рис.
8.18.
Модель
простого
перекрестка
с
учетом
потоковой
скорости
Будем
считать,
что,
кроме
индивидуальных
перемеще
ний
АТС,
которые
осуществляются
по
правилам,
анало
гичным
прщшлам, принятым
в
.модели
§8.2,
за
каждый
такт
времени
в
модели,
исследуемой
в
настоящем
пара
графе,
осуществляется
перемещение
всего
множества
АТС
как
единого
целого
на
k
клеток
вперед.
Если
перемеще
ние
АТС,
находящихся
на
второстепенной
дороге
в
теку
щий
момент
времени
на
k
клеток
вперед
недопустимо
из-за
