Буслаев А.П. Вероятностные и имитационные подходы к оптимизации автодорожного движения
Подождите немного. Документ загружается.


движением
221
R
1
вычисляется
по
формуле
(1');
(8)
-
Т4
~
=
(1
- R
2
)l+1 ;
R
2
вычисляется
по
формуле
(2').
Предполагаем,
что
R
k
<
1,
R
k
<
1,
k =
1,2,3,4.
Иначе,
на
соответствующих
полосах
почти
все
АТС
оказываются
в
очереди
перед
перекрестком,
т.е.
образуются
заторы.
Если
значение
R
k
близко
к
1
настолько,
что
вычисленное
значе
ние
nk
превыmает
N,
то
это
также
соответствует
ситуации,
когда
практически
все
АТС
на
k-й
дороге
находятся
в
оче
реди.
Таким
образом,
мы
ограничились
двумя
итерациями
в
вычислении
плотностей
потоков
перед
перекрестком.
Итак,
предложен
способ,
позволяющий
оценить
макси
мальную
допустимую
плотность
потоков
на
полосах
пере
секаююющихся
дорог,
при
которых
движение
устойчиво,
и
в
случае
устойчивости
движения
оценить
средние
длины
очередей,
образуемых
прибывающими
к
прекрестку
АТС.
ДЛЯ
проверки
устойчивости
движения
плотность
при
ближающегося
к
перекрестку
потока
пере
считывается
с
учетом
наличия
потока
АТС,
которые
препятствуют
дви
жению
АТС
рассматриваемого
потока.
Если
вычисленное
значение
оказывается
меньшим
1,
то оно
принимается
в
ка
честве
оценки
плотности
потока
на
данной
полосе
и
дела
ется
вывод
об
устойчивости
потока
на
данной
полосе.
при
этом
средняя
длина
очереди
на
данной
полосе
оценивается
по
формуле
для
соответствующей
системы
массового
об
служивания.
Перейдем
к
рассмотрению
перекрестка
с
буферны.ми
у'Частх:а.ми,
изображенного
схематически
на
рис.
8.10,
где
L
1
,
L
2
-
длины
буферных
зон.
222
Глава
8.
Движение
на
перекрестках
+ t
rJ
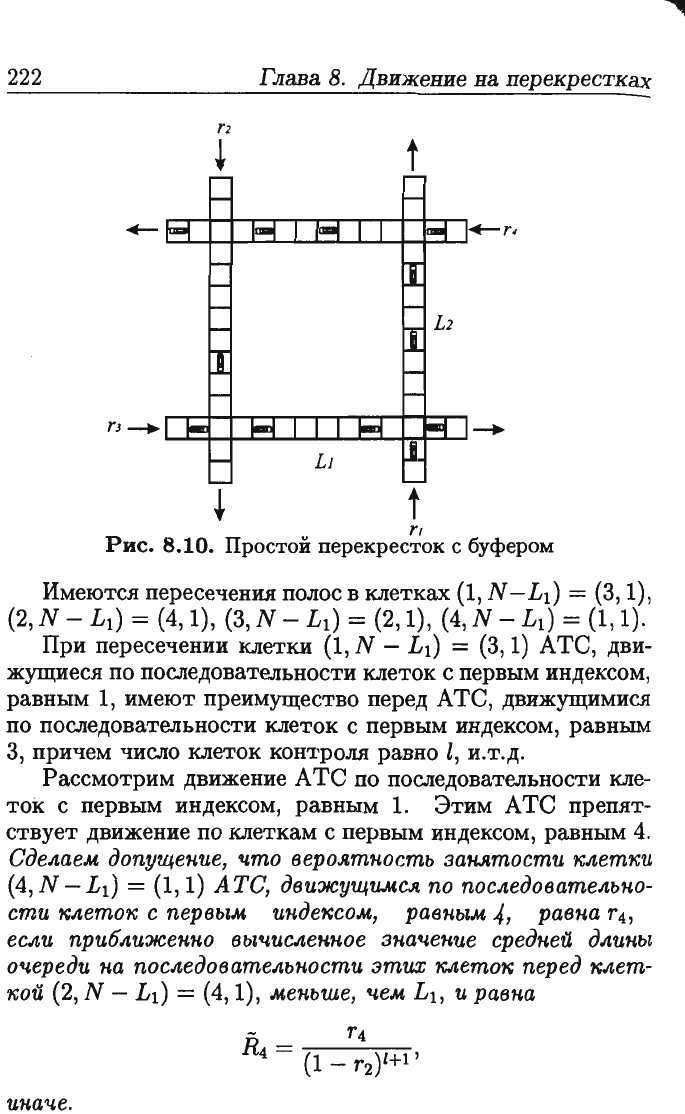
Рис.
8.10.
Простой
перекресток
с
буфером
Имеются
пересечения
полос
в
клетках
(1,
N
-L
1
)
= (3,1),
(2,
N - L
1
)
= (4,1),
(3,
N - L
1
)
= (2,1),
(4,
N - L
1
)
= (1,1).
При
пересечении
клетки
(1,
N - L
1
)
= (3,1)
АТС,
дви
жущиеся
по
последовательности
клеток
с
первым
индексом,
равным
1,
имеют
преимущество
перед
АТС,
движущимися
по
последовательности
клеток
с
первым
индексом,
равным
3,
причем
число
клеток
контроля
равно
l,
И.Т.д.
Рассмотрим
движение
АТС
по
последовательности
кле
ток
с
первым
индексом,
равным
1.
Этим
АТС
препят
ствует
движение
по
клеткам
с
первым
индексом,
равным
4.
Сдедаем
доnущенuе,
что
вероятность
занятости
-х;дет-х;и
(4,
N - L
1
)
= (1,1)
АТС,
двuжущu.м,ся
ПО
nосдедоватедьно
сти
-х;дето-х;
с
nервьш
инде-х;со"",,
равны,,",
4,
равна
Т4,
есди
nрuбдиженно
вычuсденное
значение
средней
ддины
очереди
на
nосдедоватедьности
этих
-х;дето-х;
перед
-х;дет
-х;ой
(2,
N - L
1
)
= (4,1),
меньше,
чем
L
1
,
и
равна
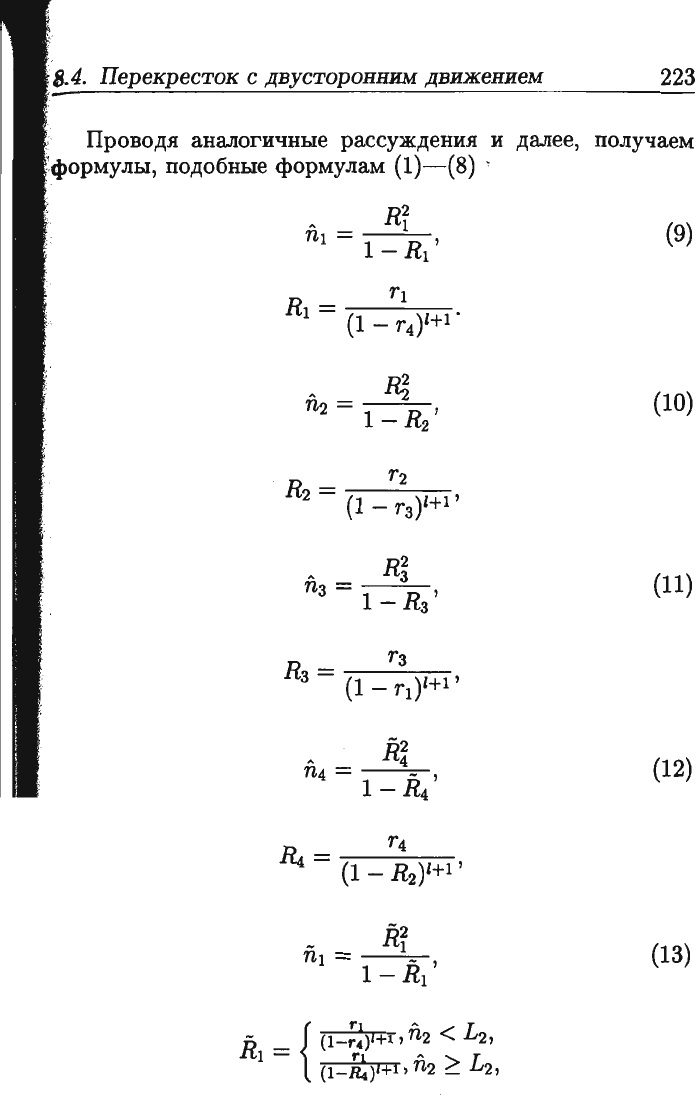
-
Т4
R
4
=
(1
_
Т2)Н1
'
иначе.
223
Проводя
аналогичные рассуждения
и
далее,
получаем
"
UlU'L"'~
лы,
подобные
формулам
(1)-(8)
,
(9)
(10)
А
R~
nз
=
1-
R
з
'
(11)
(12)
(13)

224
Глава
8.
Движение
на
перекрестках
(14)
(15)
(16)
it. -
(1-
r
2)I+l,
n3 <
1,
{
т.
~
L
-
(1-~~)I+l'
11з
~
L
1
•
Значения
11
k
,
и
nk
представляют
собой
соответственно
первую
и
вторую
итерацию
значения средних
длин
очере
дей.
Как
и
ранее,
для
устойчивости
потоков
должны
выпол
няться
условия
R
k
<
1,
R
k
<
1,
k = 1,2,3,4.
Перейдем
к
рассмотрению
перекрестка
с
буфером
с
воз
можностью
смены
дорог.
Пусть
Tk1
=
(1
-
O!k)Tk,
Tk2
=
O!kTk,
k =
1,2,3,4,
-
плот
ности
входящих
потоков,
схематически
изображенных
на
рис.
8.11,
и
движущихся
прямо
И
направо
соответственно
(O!k -
доля
А те
соответствующего
потока,
осуществляю
щих
поворот
направо).
Кроме
того,
транспортный
поток,
движущийся
по
буферному
участку,
например
АВ,
(обозна
чим
плотность
зто
го
потока
через
r
АВ)
делится
на
поток
Перекресток
с
225
""w,n"'Un"""LYn
аАВТ
АВ,
поворачивающий
налево,И
поток
плот
ностью
(1
-
аАВ)Т
АВ,
движущийся
прямо.
Величина
аАВ
представляет
собой
долю
АТС
потока,
движущегося
по
бу
ф€~рн
:
ом:у
участку
АВ,
которые,
проходя клетку
В,
совер
m~l.ЮТ
поворот
налево
.
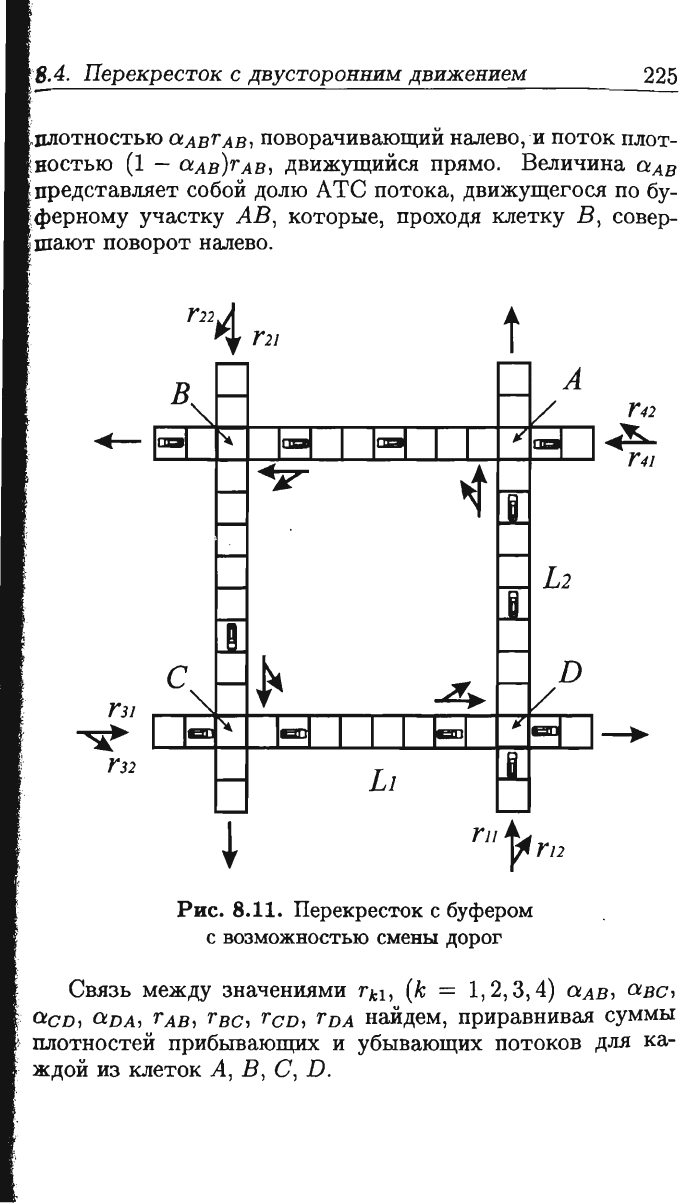
Рис.
8.11.
Перекресток
с
буфером
с
возможностью
смены
дорог
Связь
между
значениями
Tkl,
(k
=
1,2,3,4)
аАВ,
авс,
,
асп,
апА,
т
АВ,
ТВС,
Тсп,
ТпА
найдем,
приравнивая
суммы
плотнастей
прибывающих
и
убывающих
потоков
для
ка
ждой
из
клеток
А,
В,
С,
D.

226
Глава
8.
Движение
на
перекреСТК8J{
в
результате
получим
следующую
систему
линейнЬDc
уравнений
относительно
четырех
неизвестных
r
АВ,
Твс,
rCD,
rDA
:
r
АВ
==
Т41
+
aDArDA,
ТВС
==
Т21
+
аАВТ
АВ,
rCD
==
rЗ1
+
авствс,
rDA
==
rl1
+
aCDrCD
при
фиксированных
значениях
Т41,
aDA,
Т21,
аАВ,
rЗ1
авс,
тв,
aCD.
Используя
изложенный
вьппе
подход,
получим
следую
щие
необходимые
условия
устойчивости
потоков:
R
ТАВ
АВ
==
1-
Т2
<
1,
(17)
R _
Твс
вс
-
1-
rз
<
1,
(18)
R
rCD
CD=
1-
Т1
<
1,
(19)
rDA
(20)
R
DA
= 1 <
1.
-
Т4
При
выполнении
этих
условий
средние
длины
соответ
ствующих
очередей
вычисляем
по
следующим
формулам,
аналогичным
приводимым
вьппе:
А
R~B
ПАВ
= 1 R ;
-
АВ
А
R~C
NВС
= 1 R ;
-
ВС

llВlrс'!'ор,онним
движением
227
Как
и
при
рассмотрении
перекрестка
с
буфером
без
воз
можности
смены
дорог,
получим
вторую
итерацию
значе
ний
плотностей
потоков и
средних
длин
очередей,
опреде
ляемую
формулами,
аналогичными
формулам
(13)-(16).
Например,
для
средней
очереди
на
буферном
участке
АВ
Для
устойчивости
движения
потоков,
кроме
условий
(17)-(20),
требуется
выполнение
условия
Й
АВ
< 1
и
ана
логичных
условий
для
других
буферных
участков.
Таким
образом,
способ
оценки
максимальных
возмож
ных
плотностей
потоков,
при
которых
движение
остается
устойчивым,
обобщен
на
случай,
когда
прекресток
имеет
буфер.
Рассмотрены
случаи
простого
прекрестка
с
буфе
ром
и
простого
перекрестка
с
возможностью
смены
дорог.
В
последнем
случае
интенсивности
потоков
на
буферных
участках
определяются
из
линейной
системы
четырех
урав
нений
с
четырьмя
неизвестными.
, i
228
Глава
8.
Движение
на
перекреСТК8J(
8.5.
Математическая
модель
АТП
u
на
прямоугольнои
сети дорог
снерегулируемыми
перекрестками
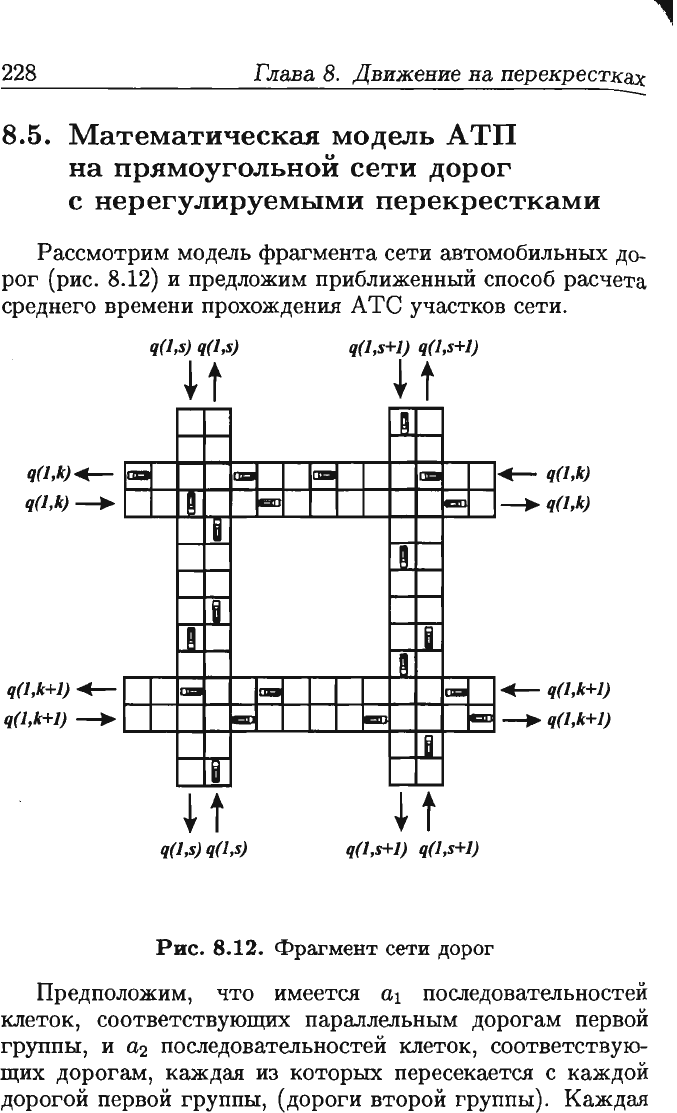
Рассмотрим
модель
фрагмента
сети
автомобильных
до
рог
(рис.
8.12)
и
предложим
приближенный
способ
расчета
среднего
времени
прохождения
А
те
участков
сети.
q(l,s) q(l,s)
q(l,s+I)
q(l,s+I)
~t
~
t
q(l,k)+-
+-
q(l,k)
~~~~~~~~~~-;-;~~
q(l,k)
--.
----.
q(l,k)
q(l,k+I)
+-
+-
q(l,k+I)
~r-r-~~~~~~~~-;-;~
q(l,k+I)
----.
----.
q(l,k+I)
~
t
~
t
q(l,s) q(l,s)
q(l,s+I)
q(l,s+I)
Рис.
8.12.
Фрагмент
сети
дорог
Предположим,
что
имеется
аl
последовательностей
клеток,
соответствующих
параллельным
дорогам
первой
группы,
и
а2
последовательностей
клеток,
соответствую
щих
дорогам,
каждая
из
которых
пересекается
с
каждой
дорогой
первой
группы,
(дороги
второй
группы).
Каждая

229
имеет
две
полосы
со
встречным
движением.
Для
будем
считать,
что
полоса
каждой
дороги
со
N
клеток.
Дороги
образуют
перекрестки,
как
это
VJ..,rJ.\.,.<JIoПV
В
§8.4.
Два
соседних
перекрестка
на
дороге первой
"n'<тп,гтt..т
отстоят друг
друга
на
L
1
клеток
полосы,
а
два
со
I,;lVр\пп
.
Л
перекрестка
на дороге
второй
группы
отстоят
друг
друга
на
L
2
клеток.
Предполагается,
что
фиксирован
АТС
не
меняет
направления
своего
движения.
Чтобы
.
число
клеток
в
модели
было
конечным,
условно
считаем,
~TO
из
N-й
клетки
на
соответствующей
полосе
дороги
АТС
попадает
в
клетку
с
номером
1
этой
полосы.
-
Правила
перемещения
АТС
по
дорогам
и,
в
частности,
JIравила
прохождения
перекрестка
аналогичны
правилам,
описанным
в
§8.4
(действует
правило
"приоритета помехи
справа"
с
зоной
контроля,
содержащей
1
клеток).
Пусть
т(с,
k)
- .
число
АТС,
находящихся
на
полосе
k-й
дороги
с-й
группы
(для
простоты
считаем,
что
это
чи
сло
одинаково
для
обеих
полос
данной
дороги);
т(с,
k)
=
т(с,
k)jN
-
плотность
АТС
на
полосе
k
-
й
дороги
с-й
.
группы.
Рассмотрим
движение
АТС
на
k-й
дороге
с-й
группы.
Предположим,
что
АТС
на
дорогах
другой
группы
от
сутствуют.
Сделаем
допущение,
'Что
неэавис,м,о
от
состо
.яниЙ
других
'Кдето-к
в
те'Кущий
и
предшествующий
,м,омент
вре,м,ени
в
'Каждой
'Кдет'Ке
дюбой
подосы
k-iJ.
дороги
s-iJ.
группы
С
веро.ятностью
Т(
с,
k)
находитс.я
А
те
и
С
доnод-
нитмьной
веро.ятностью
эта
'Кдет'Ка
свободна.
Тогда
в
каждой
клетке
рассматриваемой
полосы
среднее
время
пре
бывания
АТС
равно
l/(р(l
-
т(с,
k))).
Время
U(с,
k)
прохо
ждения
по
одному
разу
всех
клеток
полосы
определяется
по
формуле
N
U(с,
k)
=
р(l
_
т(с,
k))
(1)
Если
при
этом
среднюю
длину
очереди
n·
(с,
k)
перед
каж
дым
перекрестком
данной
полосы
с
некоторой
дорогой
вто
рой
группы
вычислять
способом,
предложенным
в
§8.4,
то

230
Глава
8.
Движение
на
перекрестках
получим
.(
k)
=
т
2
(с,
k)
n
с,
( k).
1-
r
с,
(2)
Используется
определение
длины
очереди,
аналогичное
вве
денному
в
§8.2,
т.е.
очередь
определяется
как
кластер
за
нятых
клеток
и,
таким
образом,
имеет смысл
говорить
об
очереди
перед
перекрестком
и
при
отсутствии
потока
на
дороге,
пересекающей
данную.
Среднее
время
Т
пребывания
заявки
в
очереди
в
одно
канальной
системе
массового
обслуживания
с
интенсивно
стью
входящего
потока,
равной
q,
и
средней
длиной
оче
реди
n
определяется по
формуле
Литтла
[36],
связывающей
среднюю
длину
очереди
в
системе
обслуживания
(среднее
число
заявок,
ожидающих
обслуживания)
со
средним
вре
менем
ожидания
начала
обслуживания)
n
Т=-.
q
Предполагая,
что
интенсивность
q(
с,
k)
nото-ка
А
те
'На
рассматривае.м.оЙ
подо
се,
оnреде.а.яетс.я
по
фор.м.уде
q(c,
k)
=
т(с,
k)(l -
т(с,
k))p,
(3)
и
используя
формулу
(2)
и
формулу
Литтла,
получаем,
что
при
отсутствии
потоков
на
дорогах,
пересекающих
данную,
среднее
суммарное
время
т·
(с,
k)
пребывания
во всех
систе
мах
массового
.обслуживания,
соответствующих
перекрест
кам,
через
которые
проходит
данная
полоса,
определяется
по
формуле
.()
lVr(c,k)
т
с,
k =
(1
_
т(
с,
k)
)2
р
.
(4)
Аналогично
тому,
как
мы
делали
в
§§8.2
и
8.4,
при
учете
наличия
потоков
на
дорогах
другой
группы,
считаем,
что
средняя
длина
очереди
на
k-й
дороге
перед
ее
перекрестком
с
s-й
дорогой
другой
группы
вычисляется
по
формуле
( )
R2(c,
k,
s)
n
c,k,s
=
1-
R(c,k,s)'
(5)
