Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений
Подождите немного. Документ загружается.


-3,0 -2,0 -1,0
РИС. 30
По суммам, приведенным в пос-
'еднен строке таблицы, находим на-
/ чальные моменты
«* = —2,74/32 = —0,086;
а* = 41,16/32 = 1,287;
а* = — 2,16/32 = — 0,068;
а* = 135,54/32 = 4,235.
Величины Цг
=
Ь
28
- •= °-
182
>
Е
*
=
—0,394. Неравенства (2.17) и (2.18)
также соблюдаются. Расхождения в значениях начальных моментов, вычислен-
ных по несгруппированным и сгруппированным данным, объясняются сравни-
тельно небольшим объемом выборки.
В лрил. XIII.3 приведена программа для вычисления начальных моментов
а*
8
, (5 = 1, 2, 3 и 4) для калькулятора «Электроника БЗ-21».
В результате исследования невязок треугольников приходим к выводу,
что рассматриваемый ряд подчиняется нормальному закону распределения и
/Ид = 0, так как:
1) среднее арифметическое значение практически равно нулю;
2) ни одна из ошибок Д( не превышает 3т;
3) коэффициенты и к
г
близки к их теоретическим значениям;
4) на основании критерия Пирсона вероятность р = 0,981 > 0,1 достаточ-
но велика;
5) эмпирические асимметрия и эксцесс удовлетворяют неравенствам 8% <
< ЗИЦ, \Е\ < 5Я
г
„
Построим гистограмму и выравнивающую кривую (рис. 30). Ординаты у =
= ф(<) вычислим с помощью таблицы прил. II. Результаты вычислений записы-
ваем в табл. 8.
Напомним, что высоты прямоугольников
— *<) = <2^/0,55 приведены ниже.
гистограмми
Л = <2г/(*«-1
—
Номера
интервалов
л.
1
0,398
2
0,113
3
0,227
4
0,056
5
0,056
6
0
Номера
интервалов
7
0,284
8
0,342
9
0,227
10
0,056
11
0,056
12
0
На выбор масштаба наложено лишь условие наглядности.
Таблица 8
Границы
интервалов
V'-
УТ
т уу
1
0
2
0,5
3
1,0
4
1,5
5 2,0
6 2,5
7
3,0
0,564
0,498
0,342
0,183
0,076
0,025
0,006
0,645
0,645
0,645
0,645
0,645
0,645
0,645
64

Таблица 29
№ Ошибки №
Ошибки №
Ошибки
п/п
А
п/п
А
п/п
А
1 —0,68 15
+1,09
29 + 1,61
2
+0,53
16
—0,03
30
—0,50
3 + 1,13
17
+0,18
31
-1,10
4
—1,23 18 —0,06 32
+ 1,21
5
+ 1,14
19
—0,05
33
— 1,49
6 +0,28
20
+0,77 34 + 1,12
7
+ 1,72
21
+0,14
35
+0,09
8
—0,30
22 +0,52
36 —0,13
9
+0,16
23
-0,12
37
—0,30
10
—0,27
24
+0,18
38
—1,17
11
—2,01
25
—0,29 39
+ 1,60
12
— 2,14
26 —0,05 40 —0,56
13 + 1,42 27
—0,02 41
+0,40
14
—0,47 28
—1,86
42
+0,40
2.9. Из таблиц равномерно распределенных случайных величин
(см. прил. X) сделать выборку объема л = 30 и проверить гипотезы о том, под-
чиняется ли данный ряд величин закону равномерного распределения.
2.10. Из таблиц нормально распределенных случайных величин
(см. прил. XI) сделать выборку объема я = 30 и проверить гипотезу о норма-
льности закона распределения.
2.11. С помощью таблиц нормально распределенных случайных величин сос-
тавить выборку объема п — 30 с математическим ожиданием М
х
= 1 и с. к. о.
о = 2+ 0,1/, где I — номер фамилии студента по списку группы в журнале,
и проверить гипотезу нормальности распределения.
Указание. В таблице приведены нормально распределенные случай-
ные величины (. Для того чтобы составить свою выборку, необходимо восполь-
зоваться формулой, запрограммированной для калькулятора «Электроника
БЗ-21» (прил. XIII.13),
Х1 = М
х
+ 1а
х
. (2.20)
2.12. В табл. 9 даны истинные ошибки измерения 42 углов. Испытать, под-
чиняется ли этот ряд измерений нормальному распределению. Построить гис-
тограмму, кривую распределения, применить критерий Пирсона. Вычислить
эксцесс и асимметрию [каждый студент не принимает во внимание 3 ошибки,
номера которых равны I, I + 1, / + 2 (см. задачу 2.11)].
§ 18. ОЦЕНИВАНИЕ ПАРАМЕТРОВ ЗАКОНА РАСПРЕДЕЛЕНИЯ
Как указывалось в § 16, одной из основных задач математической
статистики является задача оценивания неизвестных параметров за-
кона распределения. Эта задача является основной и в теории оши-
бок измерений.
Оценкой а* для такого значения параметра а (например, математи-
ческого ожидания) является любая функция элементов выборки
«* = а* (х
г
, *
2
, ..., х
п
).
85

Таких функций можно подобрать очень много. Однако среди них
следует выбрать те, которые в определенном смысле будут «наилучши-
ми». Разумно потребовать, чтобы эти наилучшие оценки обладали
следующими свойствами:
1) состоятельности, т. е. вер Нт а* = а\ (2.21)
Л-усю
2) несмещенности М
а
. = а; (2.22)
3) эффективности = тт. (2.23)
Последнее свойство означает выбор из всех оценок а* наиболее
точной. Оценки, обладающие указанными свойствами, называются
доброкачественными.
Существует три способа определения оценок: метод моментов,
метод максимального правдоподобия и метод наименьших квадратов.
Метод моментов заключается в замене теоретических моментов их
эмпирическими моментами, при этом математическое ожидание за-
меняется средним арифметическим (см. § 16). Этот способ наиболее
простой, но не всегда приводит к доброкачественным оценкам.
Метод максимального правдоподобия, предложенный Р. Фишером,
заключается в следующем. Аналогично плотности распределения
Ф (д;
г
) составляются функции правдоподобия Ь
1
= Ь(х
(
, а
и
а
2
, ..., а),
где — параметры распределения. При нормальном законе их два:
О) = М
х
и а
г
— ох. в отличие от ф(хг) является функцией пара-
метров а
г
, а не х
{
. Далее, если все х
{
независимы, составляется функ-
я
ция правдоподобия выборки Ь = Ь^^... Ь
п
= {~|
После этого находят оценки под условием Ь = шах, для чего не-
обходимо составить и совместно решить I уравнений:
дЬ/да, = 0. (2.24)
Удобнее, однако, получить функции 1п Ь и решить систему уравне-
ний вида
д
1п
Цда
{
= 0. (2.25)
Результат будет тот же, что и при решении (2.24).
Фишер доказал, что оценки, полученные по методу максимального
правдоподобия, хотя принцип Ь — шах не имеет теоретического обо-
снования, будут всегда состоятельными и эффективными, хотя иногда
смещенными. Но смещение легко устраняется.
Метод максимального правдоподобия, как видно, требует знания
закона распределения случайной величины X. Широко распростра-
ненным является также метод наименьших квадратов оценивания па-
раметров, не требующий знания закона распределения (этот метод
изучается во второй части курса).
Оценки, полученные по методу максимального правдоподобия и
методу наименьших квадратов, в случае нормального закона распре-
деления совпадают.
86

2.13. Пусть дана повторная выборка х
и
х
2
, ..., х
п
из нормальной совокуп-
ности. Получить рценку для неизвестного параметра ^ = М
х
, применяя метод
максимального правдоподобия.
Решение. Составляем функцию правдоподобия
V
(
1 -
; а
и далее функцию правдоподобия всей выборки
Ц = -—-е (2.26)
с
п
V (*,_,).
1=1
/ 1 У 1 7*
Ь = ..!„=(— )
логарифмируя выражение (2.27), получаем
1п
I. = 1п (У^Г" - я
1п о
- •
Дифференцируя 1п1 по а
1
, находим
п
2 2
д
1п
г=1
(2.27)
2а
2
(2.28)
Приравниваем к нулю эту производную и, заменяя поэтому точный параметр
в! его оценкой а
{
, получим
2 (*,о.
Отсюда, так как о
2
ф 0,
л п
ф
= (2.29)
1=1
и, наконец,
а\ = х= ^ XI п.
1=1 I
(2.30)
Величину х называют простой арифметической срединой.
Заметим, что из уравнений (2.29) сразу следует
л
2 = 0, (2.31)
<=1
а также свойство
п
— *)
г
= т!п, (2.32)
так как тогда максимальной будет функция (2.27).
87

2.14. В условиях предыдущей задачи найти оценки для а
х
= М
х
и а
2
а
2
, т. е. когда неизвестна и дисперсия выборки.
Решение. Перепишем выражения (2.26) и (2.27) в виде
(*/-
а
0*
1 2 а,
Ц = — е ;
/2я а
2
' г
V У й /
Далее получаем
а»
2
«
2
<"
(2.33)
1 Г 1 1ЛГ
п
I Е — «1)"
1п1 = — я
1п
у 2п — — 1па, — —
и составляем два уравнения
д 1п Ыда^ = 0, дЫ/да
г
= 0,
что дает, как и ранее, выражение (2.26) н
д
1п
^ _ п Е (х{ — а,)
2
да
г
2а
г
+
2а|
Приравнивая к нулю уравнение (2.33), получаем
л ч*<-*;)
2
Решая совместно уравнения (2.28) и (2.34) , получаем для оценки а^ вновь
V, а для оценки а*
2
выражение
«2 = 2 (*< - X )
2
^л. (2.35)
2.15. В условиях нормальной повторной выборки оценить дисперсию, если
параметр известен.
•
п
Ответ: а
2
= 2(д:
4
— а^'/л.
2.16. Доказать эффективность оценки х, учитывая, что дисперсия оценки,
если она эф>фектиЕна, выражается формулой Г. Крамера.
1
О . = — —
а
> п
(2.36)
Указание. Учесть, что дисперсия величины х =>о
2
/я. и показать,
что выражение (2.36) также приводит к указанному значению.
2.17. Доказать справедливость тождества
2(" -
м
х)
г
а\ = — - - (х-М
х
)К (2.37)
88

2.18. Учитывая (2.37) и применяя свойства математического ожидания,
показать, что
М * = о». (2.38)
2 П
Из формулы (2.38) следует, что оценка дисперсии (2.35) смещена. Несмещен-
ной оценкой, очевидно, будет
или
2 (*»-*>'
= (2.39)
п —
1
В теории ошибок измерений выражение (2.39) называют формулой Бесселя.
Ее записывают еще в виде т
%
= \гР\1(п — 1).
п
Символ [ ] называют гауссовой суммой; в отличие от символа 2 он не со-
провождается указанием пределов суммирования, предполагая, что суммирова-
ние выполняется по всем I.
2.19. Доказать, что
«*= 2(*«-
в
х)
,
^
я
(
2
-
4
°)
(см. 2.15) является несмещенной оценкой дисперсии а
2
в случае, когда известен
параметр
В теории ошибок формулу (2.40), если а
г
= М
х
= X, т. е. если отсутству-
ют систематические ошибки измерений, называют формулой Гаусса и записыва-
ют в виде
т
2
= [Д
2
]/л. (2.41)
В том случае, когда в измерениях содержится постоянная систематическая
ошибка с = Л1д , вместо (2.41) следует применять формулу
т
2
= [Д
2
]/л — с
2
, (2.42)
которая следует из выражения (2.37). Если величина с неизвестна, то в формуле
(2.42) следует использовать оценку с=[Д]/л, т.е. применять формулу
2.20. Из таблиц нормально распределенных случайных чисел сделать выбор-
ку размера п = 30 и вычислить по формуле Гаусса оценку дисперсии а
2
= 1,
рассматривая 1{ как истинные ошибки.
2.21. Сделать то же самое по формуле (2.42'), исказив значения случайных
ошибок систематической ошибкой с = 1 по формуле (}{ = + с.
Приведем формулы
о» ж о2/2 (я — I), (2.43)
е*
т
*юЧ2п, ' (2.44)
89
Номер
Значения Разности
измерений
"1
«1
1
90°15' 27,5"
+2,2
2
29,7
0,0
3
29,7
+ 1,2
4
30,9
+3,7
5
34,6 —0,5
6
34,1 -2,8
7
31,3
+2,2
8
33,5
+3,8
9
37,3
10
33,6
-3,7
X 32,2"
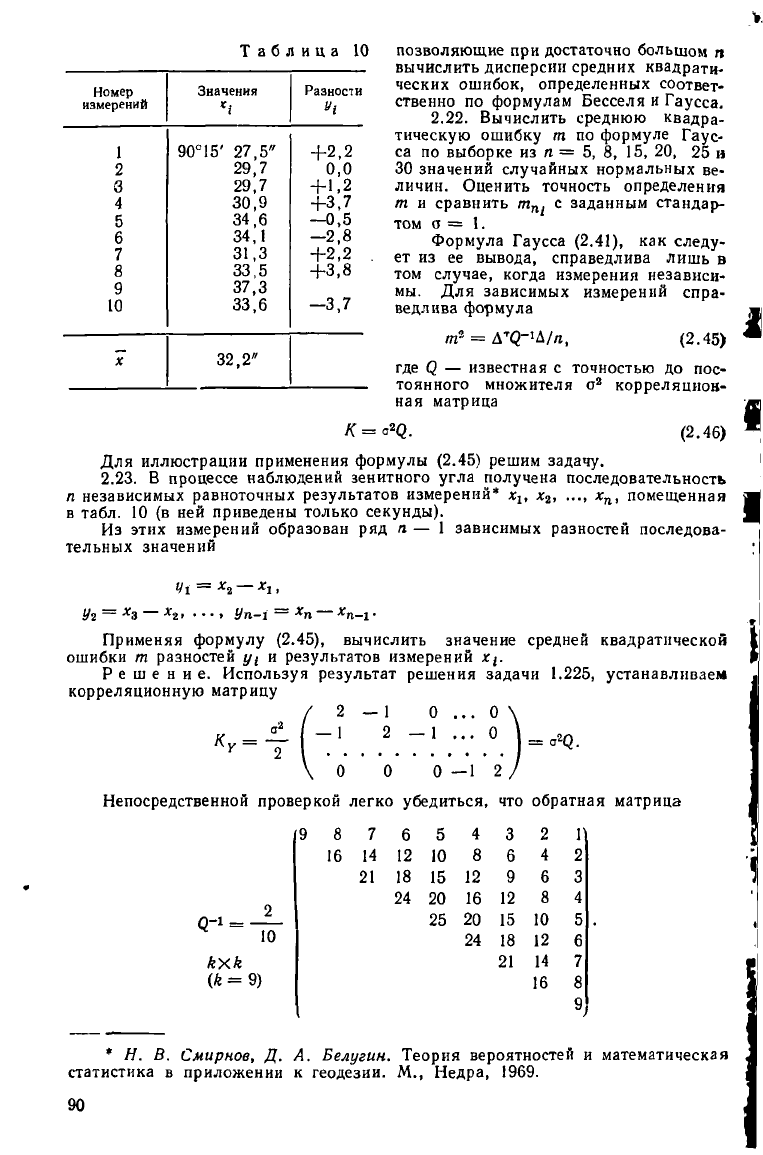
Таблица 10 позволяющие при достаточно большом п
вычислить дисперсии средних квадрати
ческих ошибок, определенных соответ
ственно по формулам Бесселя и Гаусса
2.22. Вычислить среднюю квадра
тическую ошибку т по формуле Гаус-
са по выборке из п = 5, 8, 15, 20, 25 и
30 значений случайных нормальных ве-
личин. Оценить точность определения
т и сравнить т
П1
с заданным стандар-
том о = 1.
Формула Гаусса (2.41), как следу-
ет из ее вывода, справедлива лишь в
том случае, когда измерения независи-
мы. Для зависимых измерений спра-
ведлива формула
т
2 = ДЧ^Д/л,
(2.45)
где <2 — известная с точностью до пос-
тоянного множителя о
2
корреляцион-
ная матрица
к = оч?.
(2.46)
Для иллюстрации применения формулы (2.45) решим задачу.
2.23. В процессе наблюдений зенитного угла получена последовательность
п независимых равноточных результатов измерений* х
2
, ..., х
п
, помещенная
в табл. 10 (в ней приведены только секунды).
Из этих измерений образован ряд я — 1 зависимых разностей последова-
тельных значений
—
х
ч.
—
х
1,
Уг
= х
з —
х
г I
• • • >
Уп-1 —
х
п
х
п-1 •
Применяя формулу (2.45), вычислить значение средней квадратической
ошибки т разностей у
{
и результатов измерений х
Решение. Используя результат решения задачи 1.225, устанавливаем
корреляционную матрицу
2—1 0 ... 0
-
2
I 2 -1 ... 0 ,
= а2р
0—12
0 0
Непосредственной проверкой легко убедиться, что обратная матрица
9
<2-1
=
2
10
кхк
(6=9)
7
6
5
4
3
2
1'
14
12
10
8
6
4
2
21
18
15
12 9 6 3
24
20 16
12
8 4
25 20
15 10 5
24
18
12
6
21
14
7
16 8
* Н. В. Смирнов, Д. А. Белугин. Теория вероятностей и математическая
статистика в приложении к геодезии. М., Недра, 1969.
90

В общем случае для ее элементов справедлива формула (ф
-1
)^ = 2Цк — / +
+ 1)1к + 1, где I — номер строки, / — номер столбца. Далее вычисляем у
т
(Г
1
= 0, 2 (47,2 72,4 97,6, 110,8 87,0 68,2 77,4 64,6 13,8) и ^О"
1
!/ = 152,2.
Для этих вычислений целесообразно воспользоваться программой для кальку-
лятора «Электроника БЗ-21», приведенной в прил. XIII.9 и реализующей метод
накопления, или программой (прил. XIII.11), по которой выполняются пере-
множения одной и той же строки (в нашем случае у{) на любое число столбцов
матрицы а. Хотя эта программа рассчитана для случая, когда к ^ 6, ее можно
применить и для к > 6, выполняя перемножение чисел у](] > 6) с пульта.
Окончательно имеем т
у
= У 152,2/9 = 4,11".
Так как т?
У1
= т*
хм
+ т
2
^ = 2т
%
х
, то т
х
= У4,11/2 = 2,91".
Такой же результат для т
х
получим, применив формулу Бесселя (2.39).
Если пренебречь зависимостью разностей у
1г
то мы получили бы
/
V
2
1
, 61,03
тг "V — -
1
'
84
-
2.24. В табл. 11 даны невязки суммы углов треугольников ряда триангуля-
ции I класса*.
Вычислить: среднюю квадратическую ошибку суммы углов одного треуголь-
ника, среднюю и вероятную ошибку той же суммы, предельную ошибку, среднюю
квадратическую ошибку одного угла.
В табл. II приведены значения /
г
,а значения [/
2
1 вычисляются методом на-
копления, например по программе для калькулятора «Электроника БЗ-21» (см.
прил. XIII.10).
* Г. А. Бурмистров. Задачник по способу наименьших квадратов. М., Гео-
дезиздат, 1960.
Таблица 11
Номера
треугольников
Невязки
Номера
треугольников
Невязки
Номера
треугольников
Невязки
1
+0,76"
24
+0,33"
47
+0,03"
2
— 1,48
25 —1,03
48
—0,21
3
— 1,21
26
+ 1,16 49
—0,57
4
+0,52
27 —1,32 50
—0,50
5
—0,57
28
—0,04
51
—0,82
6
—0,55 29
+0,59 52
+0,31
7
+2,54
30
+0,77
53
—0,90
в —0,99
31
—1,53
54
—0,44
9
—0,24
32
— 1,06 55 + 1,09
10
+0,25 33
—0,84
56 —0,72
11 +0,50
34
+1,05
57
+0,90
12
+1,08
35
—0,61
58
+0,45
13
+ 1,45
36
—0,96
59
+0,27
14
—2,42
37
-0,16
60
+0,96
15
+0,73
38
+0,26
61
+0,53
16
+ 1,28
39
+0,46
62
—0,21
17 +2,03
40
-0,47
63
—0,35
18 .
+0,51
41
+ 1,95
64
—1,80
19
—0,10
42 +0,71 65
+ 1,39
20
—0,78
43
+0,77
66 —0,57
21
—0,76
44 +0,46
67
+3,08
22
—0,12 45
+0,92
68
+0,12
23
+0,51
46 —0,75
[Л'
а
]
+0,12
91

Таблица 12
№
№
№ №
п/п
Д
1
п/п п/п
п/п
п/п
л
г
1
—0,47 7
0,21
13
—0,18 19
0.3^
25
0,11
2
0,49
8 0,11 14
—0,04
20
—0,18
26
—0,12
3
—0,39
9 0,18
15 +0,03
21
+0,38
27
+0,05
4
—0,46
10
0,44
16
+0,34
22 +0,11
28
+0,09
5
0,11
11
0,16
17
+0,10 23
+0,31
29
+0,05
6
0,43
12
—0,42 18
+0,45 24
+0,41
30 +0,04
Решение. 1. Рассматривая невязки как истинные ошибки сумм, найдем
по формуле Гаусса
т = /[ДД]/л =/65,28/68 = 0,98";
2. Средняя ошибка
» = [ | Д | ]/л = 54,80/68 = 0,81".
Эта же ошибка & да 4/5 • |/я| = 0,80.
3. Вероятная ошибка г* — это случайная ошибка, которая находится в се-
редине ряда ошибок, расположенных в порядке возрастания их абсолютных
величин. В нашем случае 34-я ошибка равна 0,72" и 35-я — 0,73".
Эта же ошибка г* да 2/3 • т = 0,66".
4. Предельная ошибка Д
пред
= Зт = 0,98 • 3 = 2,94".
Средняя квадратическая ошибка измерения одного угла
«1 = т/уТ = 0,98/уТГ = 0,56".
2.25. Даны ошибки округлений (табл. 12)
Вычислить среднюю квадратическую, вероятную и среднюю ошибки округ-
лений. Проверить зависимости: о
окр
= а/]Аз, = УЗ/2а
окр
. '
2.26. Дана матрица
(
2,36 — 0,28 + 0,74 + 0,72 \ ]
1,88 0 0,84 \ <
1,66 —0,36 I
1
1,92/ ,
и вектор Д = (+0,40 —1,0 —0,50 +1,00)
т
.
Вычислить среднюю квадратическую ошибку т по формуле (2.45) и оценить ее
надежность.
Ответ: т = 0,72, т
п
да0.72//8" да0,25.
2.27. Пользуясь таблицей равномерно распределенных на отрезке [0 1]
случайных чисел, смоделировать ряд 40 ошибок округлений вычислить оцен-
ку для математического ожидания, среднюю в, вероятную г и среднюю квадрати-
ческую ошибку т. Установить связь между 0 и т, г и т.
Указание. Ошибки — 0,5, где = 0,015, 5 — двузначные
числа, помещенные в таблице прил. X.
§ 19. ОЦЕНИВАНИЕ С ПОМОЩЬЮ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ 1
Рассмотренный в § 18 способ оценок неизвестных параметров на- ^
зывается точечным, а сами оценки — точечными. Он имеет тот недо- I
статок, что точечная оценка а
1г
вообще говоря, не совпадает с вели- 1

РИС. 31
а -е
а
т
+е
чиной а и особенно при малом п\ кроме того, для определения ее точ-
ности необходимо знать дисперсию
Более совершенен способ оценивания посредством так называемых
доверительных интервалов. Доверительным называется такой случай-
ный интервал для параметра а, относительно которого можно с
близкой к единице вероятностью (3, называемой доверительной,
утверждать, что он содержит неизвестное значение параметра а.
Пусть для параметра а имеется несмещенная оценка а*. Тогда, если
известен закон распределения а*, интервал находится (строится)
путем решения равенства
р{\а — а*|<е} = р (2.47)
с заданной вероятностью р л; 1.
Из равенства (2.47) следует двойное неравенство
а* — е < а < а* + е, (2.48)
которое выполняется с вероятностью р. Доверительный интервал на
числовой оси можно представить в виде случайного отрезка (рис. 31).
Точка а может находиться внутри интервала, имеющего концы
а* — е; а + е, равновероятно в любом его месте.
Доверительный интервал записывают также в виде / = (/
лев
,
'прав), где 'лев
= 1
^ 'пРав = +
Доверительный интервал для параметра а = М
х
, если оценка
а* = х параметра М
х
получена по выборке из нормальной совокуп-
ности и известен стандарт аг = о/]/7Г, строится в виде
х— (а. < М
х
+ (2.49)
где коэффициент I является таким, что
Ф(/) = _^_ Г
е
=
и его находят обратным интерполированием из таблиц функции Лап-
ласа (см. прил. IV).
Если же имеем ту же ситуацию, но с. к. о. неизвестно, то довери-
тельный интервал имеет вид
х — т. < М
х
< х + т. , (2.50>
где т= т/Уп —оценка с. к. о., а коэффициент такой, что
'3
2 Г 5^(0* = р,
9»
