Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

ветствующне крайним значениям г (0,67 и 1,47) значения коэффициента

корреляции +0,59 < г < +0,90.

Следовательно, с вероятностью не менее 0,90 действительный коэффициент

корреляции может быть заключен между +0,59 и +0,90

Минимальное значение г (при данном числе измерений я = 20)

'шш = (/20Т36 - /20 )/б = 0,50.

Так как 0,50 < 0,59, прямолинейную корреляционную связь можно счи-

тать установленной

Определим о, по формуле (2.'76), хотя, как было отмечено выше, она не сов-

сем подходит в данном случае (л < 50),

а, « (1 -0,79

)//20 = 0,035.

Как следует из неравенства (2.84), учитывая, что I = 1,65, определенная с

помощью критерия Фишера величина о, равна

; = (0,90 — 0,59)/2 • 1,65 = 0,094.

Из сравнения а

и а

следует, что формула (2.76) иногда дает хорошие ре-

зультаты при л •= 20, хотя принято считать необходимым условием ее примене-

ния л > 50.

Составим теперь уравнение регрессии |Л[ на 0

I Д'I = р,д,

;

+ (|д|-

Р|д|/0

о).

Подставляя в (2.81) численные значения г, о^. б

, получим

1 40 * 1 40

I Д< I =+°.

Т^- О/+3,8-0,79-^.4,9;

| Д;| = (0,63^ + 0,70) см, (2.86)

где — расстояние, км.

Оценим приближенно надежность коэффициента регрессии

Р|Д|Д>

+0,63 по формуле (2.83)

1,40 I —0,79

следовательно, р|

« 0,63 ± 0,12.

В связи с этой задачей заметим, что уравнение регрессии вида (2.82) не име-

ет смысла, так как никто по ошибкам |А| не станет определять расстояние Ъ.

Если случайные величины X и К подчинены нормальному закону распреде-

ления, то корреляция между ними считается установленной (критерии Фишера),

когда величина

V = — /я —2 , (2.87)

У\ —г*

соответствующая значению т (2.75), не попадает в интервал

- ^ < V < У

. (2.88)

где Ур выбирается из таблиц распределения Стьюдента (прил. V) по числу сте-

пеней свободы я — 2 и вероятности (5 » 1.

104

Таблица 29

Ноыера

приемов

Значения угла

Ноыера

приемов

Значения угля

Ноыера

приемов

с сигнчля

со штатива

Ноыера

приемов

с снгнчла со штатива

Ноыера

приемов

Ноыера

приемов

От

43,21"

42,21

42,11

42,49

43,19

43,29

44,41

42,67

вет: г = 0,75

45,10"

44,02

43,22

42,57

43,62

44,93

46,53

44,59

>2; у = 2,69

+ 0,97 X; * =

40,75

42,20

41,45

41,80

42, Л4

42,37

42,27

37,26

13,94+0,65

42,84

43,46

42,46

43,71

13,79

43,19

44,43

48,46

У•

2.43. Коэффициент корреляции между двумя слу чайными величинами X и

У, подчиненными нормальному закону распределения, согласно формуле (2.75)

при п — 20 получен равным г = +0,7. Сделать заключение о наличии корреля-

ции между X и У с вероятностью Р = 0,95.

Решение. По таблицам прил. V при 18 степенях свободы и В «= 0,9

находим ^ = 2,10, так что —2,10 < V < 2,10. По формуле (2.87) имеем зна-

чение

0,7 ,—

У =— /18 =4,2,

у 1—0,49

не содержащееся в интервале (2.88). Поэтому следует признать, что X и У зави-

симы.

2.44. С помощью таблиц"нормально распределенных случайных чисел (прил.

XI) моделировать измеренные значения трех направлений х

хх

, приняв их

истинные значения равными Х

= 60°00'00,0", X, = 90°30'31,0 , Х„ = I '54)0'

00,0", а о = 3". Чнсло приемов задать равным л = 15. Вычислить коэффици-

ент корреляции г между углами

УI

— *и

Уг

~ *з —

г>

проверить гипотезу о наличии связи согласно критерию (2.88), построить урав-

- ыення регрессии у

на у, и у

на у

2.45. На геодезическом пункте был измерен угол с сигнала и со ниатива.

Установить коэффициент корреляции между этими двумя значениями угла,

проверить гипотезу о наличии связи, построить уравнение регрессии. Данные из-

мерений приведены в табл. 19.

2.46. Ниже приведены измеренные диаметр дерева Л на высоте груди в сан-

тиметрах и высота дерева Л в метрах. Найти коэффициент корреляции между Л

и А, построить уравнение регрессии А на <*.

Ответ: г = +0,96.

8 12 16 20 24 28 32 36 40

Л, 8 11 15 17 20 21 23 24 24

Если выборка многочисленная, данные сводят в корреляционную

таблицу (табл. 20).

105

Таблица 29

Элементы У

Элементы

01 Уг

У}

»л

1г

. . .

тц

. . .

\п

гг

. . .

г }

. . .

Щп

•

• •

. . .

•

. . .

• •

«к,

. . .

"п

*к

Му

У,

У»

. . .

У]

. . .

Уп

где х

, ..., х,...; х

\ у

, ..., у,..., у

— середины интервалов или

значения признаков X и У, а т

Х)

, т

х>

Х1

, ..., т

Хк

\ т

У1

, т

,..

ту

у,

ту

— соответствующие частоты; тц — частота появления

Л); V V = /V.

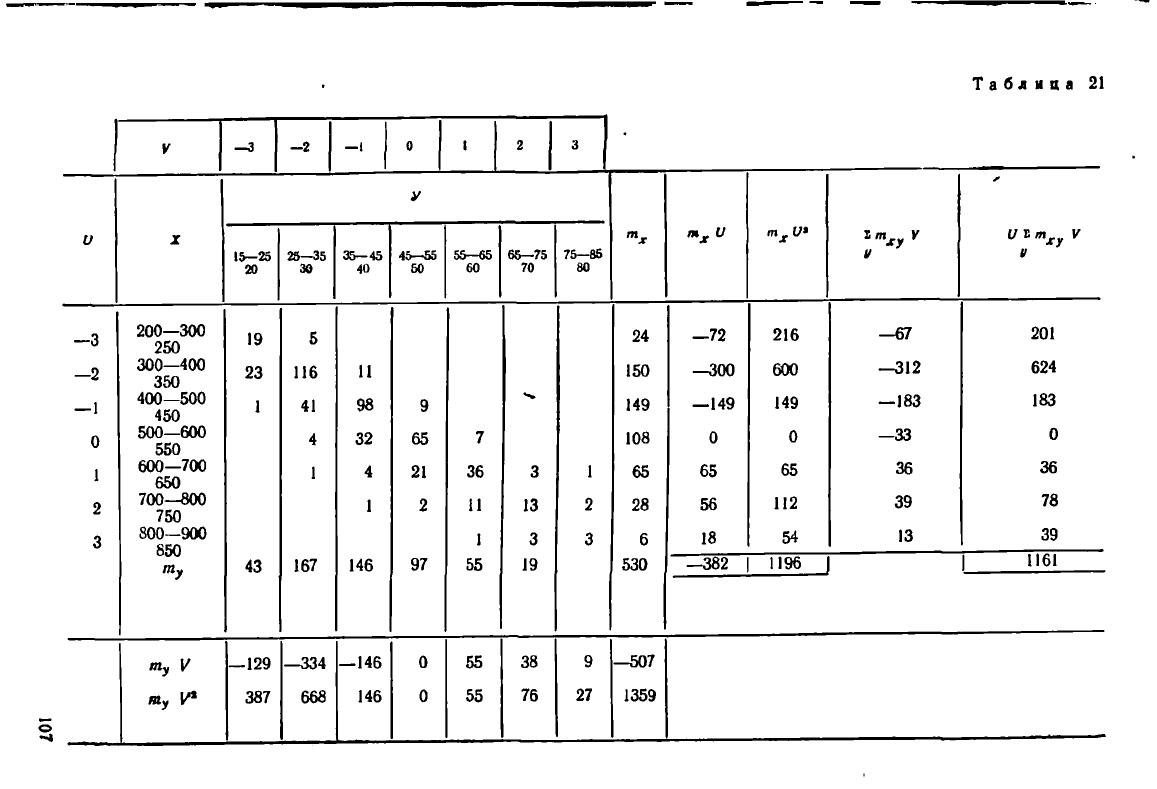
В этом случае вычисления выполняют, как показано на нижесле-

дующем примере (табл. 21)*.

Величины и = а (X — х

) и V = р(К — у

) введены для удобства

вычислений, так как коэффициент корреляции обладает свойствами

[<х

(X — х

), р (У — у

)] = г (х, у).

В примере принято х

= 550, у

= 50, а = 0,01, Р = 0,1.

Для удобства вычислений эмпирический корреляционный мо-

мент также следует вычислять, исходя из формулы (1.98),

к-

ху

=м-

ху

-м'

м-у,

или

К\у = Ту-х.-у, (2.89)

заменяя математические ожидания средними арифметическими. В фор-

муле (2.89) обозначено

ху = 2 х

/ п.

* Л. И. Лыхотелов, И. П. Мацкевич. Руководство к решению задач по выс-

шей математике, теории вероятностей и математической статистике. Минск,

Вышейшая школа, 1969.

106

Таблица

104

—3 -2

—1

•

15—25

25—35

35—45

45—55

55-65

65—75

75—85

и>

У " т

ху

—3

200—300

250

—72

216

—67

201

—2

300—400

350

116

150

—300

600

—312

624

—1

400—500

450

149

—149

149

—183

183

500—600

550

7 108 0

—33

600—700

650

21 36 3

700—800

750

2 11 13

112

800—900

850

Шу

I 3 3 6

800—900

850

Шу

167 146

19 530

—382

1196

| 1161

800—900

850

Шу

щ V

—129

—334

—146

0 55

—507

387

668

146 0 55

1359

Эмпирические дисперсии вычисляем по формулам

=-^--~х, (2.90)

т у. (2.91)

* /I

Они более удобны для программирования, чем (2.39), так как не

нужно хранить в памяти ЭВМ признаки х

и у

. Составленные на ос-

новании этих формул для калькулятора «Электроника БЗ-21»

программы вычисления коэффициента корреляции приведены в прил.

ХШ.6.

При интервальном ряде, который имеет место в рассматриваемой

задаче, все дальнейшие вычисления выполнены по формулам:*

ц7=-!-± ^ 2,191;

N 530

= = = =

N530 N 530

2 Иу Ру . 2/71

= 1—I— = -1221 = 2,564, й

= —^ = = 2,257;

N 530 N 530

% = V

—V

= 2,564—0,916 = 1,648, ту = 1,28;

т1 = V

—V

= 2,257 — 0,520 = 1,737, т

= 1,32;

ЦУ-ЦУ

2,191 -0,690

1,501

= 0 §88

1,32.1,28 1,690

X = х

+ — = 550 + ~

0,721

= 550 — 72,1 = 477,9;

а 0,01

у =

= 50 + ~°'"

= 50 — 9,57 = 40,43.

а 0,1

Коэффициент регрессии

1,28

= г

^ = °'

888

тж

°'

0888

15Г = °'

0849

' =

0,01

Уравнения регрессии! у = 0,085, х — 0,192; х = 9,16 у + 107,56.

* В них средние квадратические ошибки и частоты обозначены одной бук-

вой, но это не должно привести к недоразумению.

108

§ 22. ОЦЕНКА ТОЧНОСТИ ФУНКЦИЙ РЕЗУЛЬТАТОВ ГЕОДЕЗИЧЕСКИХ

ИЗМЕРЕНИЙ

В § 15 мы ознакомились с решением задач на определение диспер-

сий и корреляционных матриц функций измеренных величин. В настоя-

щем параграфе приводится ряд задач на оценку точности функций

результатов геодезических измерений, точность которых характеризу-

ется заданными средними квадрэтическими ошибками, вычисленны-

ми по результатам эксперимента. Могут быть также заданы эмпириче-

ские коэффициенты корреляции или оценочные корреляционные мат-

рицы.

Формулы для вычислений средних квадратических ошибок функ-

ции

и = Цх

...х

) (2.92)

имеют вид:

а) в случае некоррелированных аргументов

--ШК

93)

1 = 1

б) для коррелированных аргументов

= 2 (Щ*

» + 2 У (—) № г, „ «, т

, (2.93')

I д

Х1

)

[дх

)

\дХ))

*1*} *<

Для системы функций (вектор-функции) и = /(X)

= АМ

. (2.94)

где Ми и М

х — соответственно эмпирические корреляционные мат-

рицы вектор-функции и вектора измерений. Матрица А определяется

согласно (1.113)*

2.47. В треугольнике измерены два угла со средними квадратическими ошиб-

ками /Пр

(

= 5", = 3". Найти т^.

Решение. Составляем функцию и = (5

=» 180° — Р

—

Далее имеем

т}

= + т^ = 25 + 9 = 34, т^ = Кз4 = 5.8'.

Вообще для линейной функции вида « =» *

3 2.2. ,2 V* 2

и =

х, +

х,

= 2л

х, ?

а для функции и = к

± ...± к

1 = (2.95)

Формула (2.93') есть частный случай (2.94) для одной функции.

109

Если Х( — одинаково округленные слагаемые, то т

= О.б/у^з~"ед. послед-

него знака округленного числа.

2.48. Угол вычислен как среднее из п его значений, найти среднюю квадра-

тическую ошибку полученного значения угла, если ошибка одного измерения

равна т.

Решение. Так как функция имеет вид С/ = ^х^п, то

1=1

\дх

)

2.49. Линия длины 5 измеряется мерным прибором длины / со средней

квадратической ошибкой одного уложения прибора вдоль линии, равной т[.

Найти среднюю квадратическую ошибку измеренной длины, пренебрегая остат-

ком.

Решение. Функция имеет вид

и= 2

х. = щ,

1=1

где п — 511. Поэтому т? = т] —

или

= т

= т, "^/у = =

(величина ц = ш//)^/ называется коэффициентом случайного влияния).

2.60. Найти средние квадратические ошибки приращений координат, вы-

числяемых в геодезии по формулам Д* = 5соза; Ау = 5зта, если длина линии

5 = 127,00 м, дирекционный угол а =• 32°00\ а ошибки т/ = 0,03м, та = 1,5'.

Решение. По формуле (2.93), выражая пи в радианной мере, находим

(вычисления выполняем на логарифмической линейке)

ггг

&х

соз® ат%

+ 5

зт

а :

^ = 0,719-9-10-

+ 161

•

10»-0,281 -0,19-10"" = 6,5-10"

+ 8,6-10"

= 15,1.10-*; = 0,04 м.

Аналогично

т\

пг

&у

= з!п

апг

+ 5

соз

а '•

т\

= 0,281-9-10"

+ 161- 10

-0,719-0,19-0,19-10"

= 2,5-10"

+ 21,8-10"

= 24,3 • 10

-4

; ш

Дй

= 0,05м.

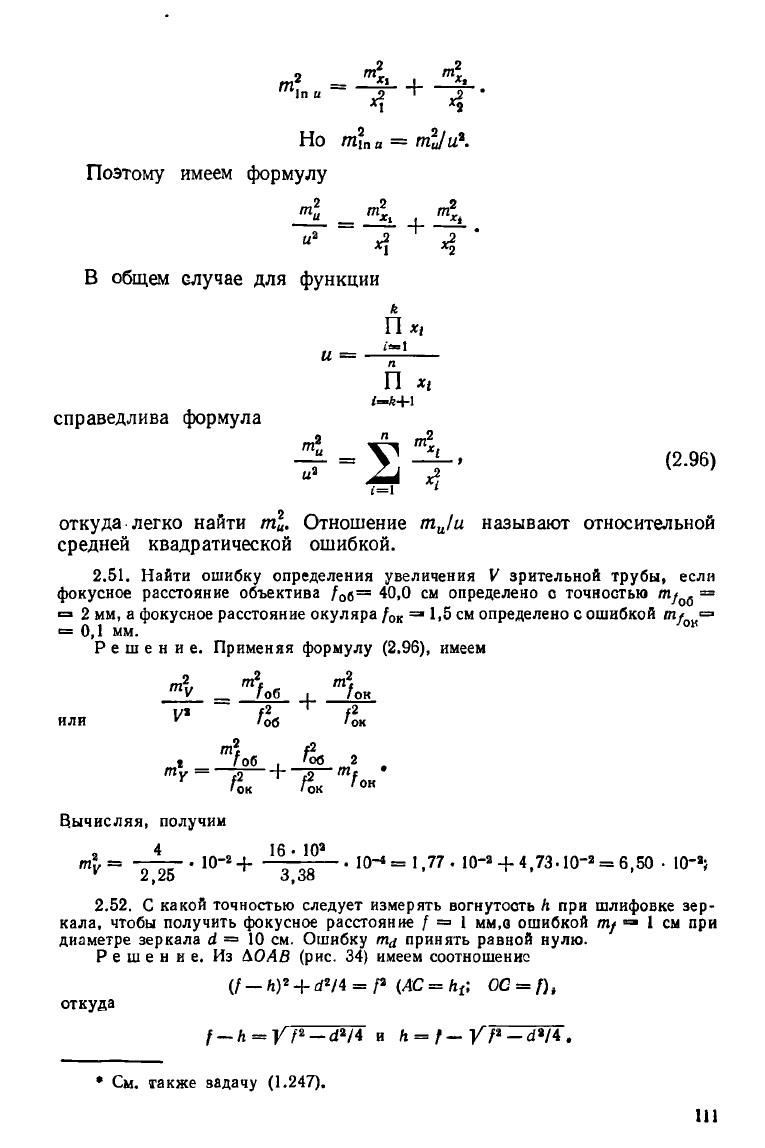
Если функция имеет вид и = х

• х\ или и = то можно

написать 1п и = 1п х^ 1п х

. Применяя теперь формулу (2.93), полу-

чим

110

„2 „2

о ОТ, ОТ,

т = 4- '

Ш и — о -г 9 •

Но т?па = т1/и*.

Поэтому имеем формулу

и _ < • <

ДГ

В общем случае для функции

и —

п *

(=•к+\

справедлива формула

1 = 1

„2

(2.96)

откуда легко найти т1. Отношение т

/и называют относительной

средней квадратической ошибкой.

2.51. Найти ошибку определения увеличения V зрительной трубы, если

фокусное расстояние объектива /

б= 40,0 см определено с точностью от/

об

= 2 мм, а фокусное расстояние окуляра /

ок

=» 1,5 см определено с ошибкой т* =>

= 0,1 мм.

ок

Решение. Применяя формулу (2.96), имеем

т\ т\ т с т I

/об I /ок

V* /

„ /

* 'об 'о

ИЛИ " /об 'ок

Я? Л «

I /Об , 'Об 2

тк=

/^К

Вычисляя, получим

"215" '

10_г +

'з'зГ •

10-4

•

10-2

73,10-2

= б.

•

2.52. С какой ТОЧНОСТЬЮ следует измерять вогнутость к при шлифовке зер-

кала, чтобы получить фокусное расстояние / = 1 мм,в ошибкой ту = 1 см при

диаметре зеркала Л = 10 см. Ошибку та принять равной нулю.

Решение. Из ДОЛВ (рис. 34) имеем соотношение

(

/ _ ну + а*14 = п (АС = ОС = П,

откуда

/ —

— У/

—4

/4 и Л = / — //

- .

* См. также задачу (1.247),

111

Находим частную производную

—— = 1

и вычисляем ее

( 4/ Л=1 мм ~ ' ~

РИС. 34

0,01

/0,9975

— 1,0013 = —0,0013.

Окончательно получим

I дН . I дН \

= /-^-1 ту, т/, = т/= 0,0013 см = 0,013 мм (к = 1 —

— 0,9987= 1,3 мм).

2.53. В радио- и светолокации время ( распространения волн в прямом и

обратном направлениях определяется формулой ( = <р/2л/, где ф — разность

фаз, / — частота колебаний. Определить ошибку если т.? = 1°, / = 10 мГц,

т^ = 0,15 кГц (приняв двойное расстояние равным 30 км).

Решение. По формуле (2.95), считая ср и / независимыми, имеем

2л/

30 км

далее вычисляет г

299792,5 км/с

= 1,01.

2тс/

10"

т] = 10-^ + (-1,01.10-

.0,15.10-з)

= (2,8.10-1»)

+ (— 151 • Ю

-10

)

, т

(

= 12,3 • Ю"» с.

2.54. Написать средние квадратические ошибки следующих функций:

1) и => 2) и = х

1б*

. 3) и = 1в*

/**, 4) и = х/2у

, 5) и = 5 з!п Р/з1п(Р

+Р

если аргументы этих функций — независимо измеренные величины с заданными

средними квадратическими ошибками.

2.55. Найти среднюю квадратическую ошибку превышения, вычисленного

по формуле Н = 1[2Ь'з1п27 + I — с + /.

2.56. Для определения коэффициента дальномера зрительной трубы кипре-

геля измерено горизонтальное расстояние от оси вращения трубы до рейки. Это

расстояние за вычетом величины постоянного слагаемого дальномера С равно

5± т

. Отрезок I рейки между дальномерными нитями сетки получен при гори-

зонтальном положении трубы со средней квадратической ошибкой т

{

Пренебрегая малыми ошибками в определении слагаемого дальномера С,

подсчитать среднюю квадратическую ошибку в найден-

ном значении коэффициента дальномера С = — при

5 = 148 м, / = 1,48 м, т

= 0,07 м и т, = 0,005 м.

Ответ: т

= 0,35.

2.57. Для определения площади прямоугольника Р

измерены две стороны: а = 203,21 м± 0, И м, й =

= 315,42 м± 0,12 м.

Вычислить площадь и ее среднюю квадратическую

рис. 35 и относительную ошибки.

112

От в е т: Р = 64096 м

, т

= 42 м

, т

1Р = 1/1500.

2.58. В прямоугольном треугольнике (рис. 35) измерены: угол А = 40°00'±

± Г, угол В = 50°00'± Г и сторона Ь = 150,00 м± 0,05 м. Вычислить по изме-

ренным углам, применяя теорему синусов, сторону а и ее среднюю квадратичес-

кую ошибку.

О т в е т: а = 125,87 м, т

= 0,068 м.

2.59. Найти относительную ошибку стороны полигонометрического хода 5,

если средняя квадратическая ошибка логарифма стороны т\

$ — 36 ед. 6-го

знака логарифма.

Решение. Функция имеет вид и = 1§5, а т

— т

1е5

Д5 о Ото

Аи = М — , т

= М

— ,

5 " 5

откуда

/М = т

/ 5 или т

/ 5 = от

1е5

/М, (2.96')

где М = 0,4343.

Подставив численные значения, получим

/5 = 36 • 10-»/0,434 = 1/1200.

2.60. Требуется определить площадь квадрата Р размером около 1 га со

средней квадратической ошибкой т

= 10 м

. С какой точностью нужно изме-

рить для вычисления площади: а) одну сторону а; б) две смежные стороны; в) диа-

гональ й, чтобы получить площадь участка с заданной точностью?

Ответ: а) т

/а = 112000; б) т

/а = 1/1400; в) т

/4 = 1/2000.

Принцип равных влияний. При решении обратной задачи оценки

точности функций — расчете точности измерений аргументов при за-

данной средней квадратической ошибке функции применяют так на-

зываемый принцип равных влияний, т. е. требуют, чтобы влияние

ошибок измерений на т

было одинаковым. Тогда из формулы (2.93)

следует

(—)

т] = —

\ дх

или

а*,

Гп

(2.97)

2.61. Горизонтальное проложение $ определяют по формуле «= Осозу.

С какой точностью должно быть измерено наклонное расстояние О и угол на-

клона у, если О да 210 м, V

Ю°, а 5 должно быть получено со средней квадра-

тической ошибкой /п, = 0,10 м?

Решение. По формуле (2.93) получаем

2 2 от

= со$

-\т

+ В

5Ш

7 —— •

Применим принцип равных влияний, т. е. потребуем, чтобы влияние оши-

бок измерений расстояния О и угла наклона

на среднюю квадратическую ошиб-

ку т

было одного порядка. Для этого должно быть

С05

^ОТд

51П

„2 _2

от

113