Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

где 5

_,(0 — плотность так называемого распределения Стьюдента

с (п — 1) степенями свободы. Для этой функции, как и для функции

Ф(/), составлены и приведены в прил. V таблицы.

Заметим, что при достаточно большом п (порядка 25 и более) для

определения коэффициента можно пользоваться таблицами функ-

ции ФЦ).

В том случае, когда математическое ожидание М

совпадает с ис-

тинным значением измеряемой величины (случай отсутствия систе-

матических ошибок), вместо выражений (2.49) и (2.50) можно написать

х — 1+/ст-; (2.51)

К X

х — (

т- < X < х-Ь/д. (2.52)

Если закон распределения оценки а* неизвестен, доверительный

интервал можно построить, применяя неравенство Чебышева в форме

с!

Р[\х-М

| <

} > I

г'

Полагая е = , получаем

Р [ | х — М

| < 1а- } > 1 . (2.53)

* I

Доверительный интервал для с. к. о. ст в случае нормальной

выборки строится в виде

Ът < а < у

т (2.54)

(в отличие от предыдущих интервалов он несимметричен относитель-

но оценки), где

Ь = / ("-О/ X?! Т

= / (л-1)/хЗ (2-55)

или

71 = Ъ = У^Рй (2-56)

соответственно, если оценка т (средняя квадрэтическая ошибка) по-

лучена по формуле Бесселя или Гаусса, а величины х?

Уз вы-

бирают из таблиц (прил. VII) так называемого распределения

с числом степеней свободы п — 1 или п соответственно по вероят-

ности = (1 — р)/2 и р

= 1 — р1*.

Построив интервал (2.54), легко получить доверительный интервал

для с. к. о. Ох простой арифметической средины, разделив все чле-

ны неравенства (2.54) на У~п. Учитывая, что т1У~п = гщ, получим

< сг- < т

т-. (2.57)

* Удобнее пользоваться таблицей (прил. VIII), которая сразу позволяет

найти величины и

С применением доверительных интервалов в ряде других случаев

мы встретимся и в других разделах пособия.

Доверительные интервалы можно применить для проверки стати-

стических гипотез. Например, если имеем ряд истинных ошибок Д

(

измерений одной величины, то для математического ожидания Мд

можно построить доверительный интервал

А - V". < < Д + (2.58)

где _ _

А = 2А

/«, /Пд = т/Уп.

При справедливости гипотезы /Ид = 0, очевидно, с вероятностью

Р должны выполнятся неравенства

А — (

т- <0; А + 1-М- > 0.

р д " д

Объединяя их в одно неравенство, получаем

А — ^ш- < 0,

откуда следует критерий

(2.59)

обнаружения систематических ошибок: если неравенство (2.59) вы-

полняется, то гипотеза об отсутствии систематических ошибок при-

нимается.

При большом п для упрощения вычислений можно принять т

= 1,250, где в = [|А1]/л — средняя ошибка. Тогда вместо (2.59) бу-

дем иметь критерий

[Л]

|д| < 1,25* ЦАЦ. или

^ 1,25/

пУТГ'

откуда следует |[АЦ < 1,25 /[ДУУп.

Принимая = 2, что соответствует вероятности р = 0,95 при

п > 30, получаем

|[Д]|<2,5[|Д|]/*Т. (2.60)

2.28. В условиях задачи 2.27 пзстроить доверительные интервалы для истин-

ного значения X измеренного угла, с. к. о. измерений а и о_ при доверительной

вероятности Р = 0,95, полагая М

х{

= X.

Решение. Согласно формуле (2.52) можно написать

90°15'32,2" — т- с X < 90°15'32,2" + т- .

Коэффициент находим из таблиц распределения Стьюдента по чис-

лу степеней п — 1 = 9. Имеем Ц =2,4. Средняя квадратическая ошибка

т- = т1Уп =2,91 //л =0,97".

Окончательно получаем

9(Н5'29,9" « Х<90°15'34,5\

Для построения доверительного интервала для с. к. о. а из таблицы (см.

прил. VII ИЛИ VIII) по числу степеней свободы п— 1 = 9 и вероятности р =

= (1 — Р)/2 = 0,025 находим ~ '9,6 и у

= 0,69, а по вероятности р

— I — р

= 0,975 и тому же числу степеней свободы определяем

2,66,

= 1,83. Доверительный интервал будет иметь вид 2,01" < а < 5,32", а для

а- будет 0,67"< о_ < 1,77".

2.29. Угол измерен 10 раз и получено среднее значение угла"* = 120°15'15"

и эмпирическая средняя квадратическая ошибка одного илмерения т = 6,0".

Определить вероятность того, что математическое ожидание угла лежит в пре-

делах от 120°15' 12,7" до 120°15'17,0".

Ответ: 0,746.

2.30. По условиям предыдущей задачи построить доверительный интервал

для математического ожидания угла (истинного значения) с доверительной веро-

ятностью Р = 0,68 и 0,997.

Ответ: 120°15'12,9" < X < 120°15'17,1"; 120°15'06,5" < X < 120°15'

23,5".

2.31. Проверить гипотезу об отсутствии систематических ошибок в условии

задачи 2.18, приняв доверительную вероятность |3 = 0,95.

Решение. Применяя формулу (2.59), напишем 0,105 ^ Ц тд-.

Средняя квадратическая ошибка '

Коэффициент = 2,0. Поэтому Iр /л

= 0,38.

Следовательно, неравенство (2.25) выполняется и можно сделать вывод об

отсутствии систематических ошибок.

т-=т!у12"= 1,10"//32 = 0,19".

Таблица 13

№

п/п

РИС. 32

0,46

0,14

2,46

—0,32

—0,07

0,30

—0,29

1,30

0,24

—0,96

0,134

—0,186

2,134

—0,646

—0,396

—0,026

—0,616

0,974

—0,086

—1,286

3,26 —8,170

Ъх,

- = 0,326,

Таблица 94

Номер

вы-

борки

Доверительный

интервал для

Т1» Т.

Доверительный

интервал

для э

0,326

2,3

2,2

2,1

1,484

—1,158; 1,810

0,69; 1,83

0,73; 1,58

0,76; 1,46

0,66; 1,74

Неравенство (2.60) приводит к результату

2,5 • 28,19

[А]

/32

или 3,39 < 12,46.

2.32. Проверить гипотезу о наличии систематических ошибок в условии

задачи 2.10.

2.33. Сделать то же самое в условиях задачи 2.11.

2.34. Из таблицы нормально распределенных случайных чисел сделать й=»

= 5 различных выборок объема = 10, гц = 15, п

= 15, гц = 15, пь = 20.

Для каяСдой выборки вычислить хат. Построить доверительные интервалы

для М

= 0 (Р = 0,95). Для наглядности нанести их на рисунок (рис. 32). Ус-

тановить, перекрывают ли они математическое ожидание М

= 0. Сделать то

же самое для стандарта о = 1. Вычисления располагать в табл. 13 и 14 (для при-

мера приведена выборка 1).

§ 20. ОБРАБОТКА РЯДА РАВНОТОЧНЫХ ИЗМЕРЕНИЙ ОДНОЙ И ТОЙ ЖЕ

ВЕЛИЧИНЫ

В § 18 мы показали, что наилучшей оценкой для математического

ожидания будет так называемая простая арифметическая средина

х = \х]1п, (2.61)

а для дисперсии одного измерения — квадрат средней квадратиче-

ской ошибки (формула Бесселя)

т» = [о«]/(п—1), (2.62)

где VI = Х{ —х — отклонения от простой арифметической средины,

обладающие свойствами:

[о] = 0, И = шт. (2.63)

Величина х имеет среднюю квадратическую ошибку

т. =м = т/\/1Г. (2.64)

258

д7

Совместное влияние случайных ошибок и постоянной системати-

ческой ошибки может быть выражено формулой

= + с

, (2.65)

где с — систематическая ошибка. Число измерений поэтому не может

беспредельно повышать точность х. Полагают [1], что должно выпол-

няться неравенство с < Ч

• т(\Гп.

Средняя квадратическая ошибка

т = У [о»]/(л — 1)

при достаточно большом п характеризуется средней квадрэтической

ошибкой

ж т/У2(п — 1). (2.66)

Заметим, что если выполняют измерения 5 однородных величин п

раз каждую, например углы на различных пунктах, то среднюю квад-

ратическую ошибку измерения можно вычислить по формуле

2 1°

= , (2.67)

»=1

где [о

]

— сумма квадратов отклонений результатов измерений от

XI на каждом пункте.

Порядок вычислений при обработке ряда равноточных измерений

следующий.

1. Вместо формулы (2.61) применяют более удобную формулу

х = У +

где х' — приближенное значение для х (обычно это минимальное

значение а

е, = — лЛ (2.68)

2. Вычисляют отклонения

— x

окр

(2.69)

и выполняют контроль

[о] яр, (2.70)

где Р — ошибка округления при вычислении х, т. е. Р = *

окР

— х.

Обычно х

окр

вычисляют с числом десятичных знаков на один больше,

чем их имеется в (х

окр

получают округлением х, т. е. х содержит

на один знак больше, чем х

0КХ1

Таблица 96

№

п/п

Результаты

измерений

с?

Контроль

- 57° 2

*окр ~ ^7

х = 57°23'

57°23' 44'

43'

3' 40" •

'23' 44,7"

44,67"

-0,7

—4,7

-1.7

+0,3

+1.3

-1.7

+3,3

+0,3

+з.з

+1.3

+2,3

-3,7

—12,5

+ 12,1

2 = —0,4

2 г/п =

=4,67"

0,49

22,1

2,89

0,09

1,69

2,89

10,9

0,09

10,9

1,69

5,29

13,7

2=72,9

т = У

М = 2,

2=56

72,9/

57/УТ

2 = 334

11 = 2,57

2 = 0,74",

!• Р = *окр— * =

= 57° 23*44,7" _

—57°23' 44,67" =

= 0,03"

— я? =0,03"-12 =

= — 0,4"

2. [с] =0,4"

3. [о

] = [е

] -

Ге

1 56

— = 334 — — =

п 12

= 72

= 0,55"

= 0,16"

3. Далее вычисляют [и

] с контролем

[0»| = [

2]_Ш1 (2.71)

и ошибки т, М, т

ж т/У2{п — 1) и тм» М/]/2п.

4. Строят доверительные интервалы

х — (

т- < X <

~х

+ ^т-; (2.72)

71 т < а < ; (2.73)

от- < 7

ие;. (2.74)

2.35. В табл. 15 приведены значения измеренного двенадцатью

приемами угла. Выполнить обработку данного ряда измерений.

Решение. Вычисления согласно приведенным выше формулам

выполняем в таблице.

Доверительный интервал для истинного значения измеряемой ве-

личины имеет вид (2.72). Приняв доверительную вероятность р =

= 0,90 по числу степеней свободы п — 1 = 11, из таблиц распределе-

ния Стьюдента находим коэффициент ^ = 2,20 и строим доверитель-

ный интервал

57° 23' 43,04" < X < 57°23' 46,30".

Доверительный интервал для е. к. о. а строим согласно (2.73).

По числу степеней свободы п — 1 = 11 и (5 = 0,90 находимо помощью

таблиц х? = 19,7 по вероятности р

{

= (1 — Р)/2= 0,05, х! = 4,6

по вероятности р

= 1 — Р\= 0,95.

4* 99

Тогда получаем

КП/19,7 • 2,57"<а<V 11/4,4 • 2,57"; 1,92"<о<4,06".

Доверительный интервал для аг будет 0,55" С от <. 1,17".

Иногда результат обработки измерений записывают в виде

х ±М, т ± т

, т-±М

или в нашем случае

57°23'44,67" ± 0,74 ; 2,57 ±0,55"; 0,74 ±0,15".

2.36. Сделать то же самое, исказив измеренные значения углов системати-

ческой ошибкой с •= 1". Сравнить результаты с полученными в предыдущей

задаче и сделать соответствующие выводы о влиянии систематической ошибки.

2.37. Решить задачу 2.34, вычисляя величины х и до целых. Сравнить

значения полученных в этом случае средних квадратических ошибок.

2.38. С помощью таблиц нормально распределенных случайных чисел смо-

делировать процесс измерения угла, истинное значение которого Х= 60°30'00,0",

п = 10 приемами с математическими ожиданием истинных ошибок М

= 0 и

с. к. о. а «= 3". Выполнить полную математическую обработку полученных та-

ким образом результатов измерений.

Указание. Каждый студент выбирает 10 случайных ошибок из полосы

таблицы (прил. XI), номер которой

совпадает с порядковым номером его фами-

лии по журналу. «Измеренные» значения углов получить с помощью табл. 16.

Таблица 16

омер прием--

0,46

0,14

2,46

-0,32

-0,07

0,30

-0,29

1,30

0,24

-0,96

д. =

Измеренный угол

1,38

0,42

7,38

—0,96

—0,21

0,90

—0,87

3,90

0,72

—2.88

60°30'

60 29

01,4"

00,4

07,4

59.0

59,8

00,9

59.1

аз,9

07.0

67.1

Таблица 17

Варианты результатов измерений, см* Варианты результатов измерений, см

№

а/и

№

п/п

41.0

41.1

40.8

41,0

40,5

40.9

40,5

41,2

41.4

41.5

40,5

40,4

41,3

40.8

40.9

41,0

40,6

40,8

40.3

40,7

40,6

40.4

41,6

41.5

41.6

40,8

40,5

40,2

40.7

41,2

40,4

41,0

41.2

40.6

40.7

41.3

40,7

40,9

40.6

40,3

41,0

41.7

40,4

40,2

40,1

40,7

41,4

41,6

41.3

41,5

41.2

41.4

40.3

40,9

41,4

40,0

41,3

40,7

41,2

40,0

100

Дальнейшие вычисления выполнять так же, как и в задаче 2.34.

2.39. При исследовании полярного планиметра было произведено 12 изме-

рений площади участка. Результаты измерений приведены в табл. 17. Вычис-

лить среднее значение и его среднюю квадратическую ошибку, а также т и т

по одному из вариантов.

2.40. Длина стороны полигонометрического хода измерена светодальноме-

ром СТ-62М шестью приемами. Результаты измерений получить с помощью таб-

лиц случайных нормальных чисел, приняв стандарт измерений а = 0,02 м,

а точное значение длины 5 = 520,00 м. Исходные данные должны быть индиви-

дуальными для каждого студента.

2.41. Измерены три угла числом приемов п

= 9, = 6, п

= 12 и полу-

чены величины [о

]! = 42,3, [о

]

= 20,0, [р

^ = 35,6. Найти среднюю квадра-

тическую ошибку измерения угла одним приемом.

Ответ: Согласно формуле (2.67) т = У97,9/(27 — 3) = 2,0".

Для решения задачи обработки ряда равноточных измерений одной и той

же величины ч прил. XIII.4 и XIII.5 приведены программы для калькулятора

«Электроника БЗ-21».

При обработке ряда измерений одной и той же величины возможен случай .

когда среди измерений х содержатся резко выделяющиеся результаты.

Н. В. Смирновым предложен критерий для их выявления. С этой целью начис-

ляется величина г = |х

— х\/т, где х

— экстремальное значение (х

тзх

или *

1п)

из XI, т

= [(Х{ — х)

]/п, х — среднее арифметическое из дРаспределение ве-

личины г зависит только от числа измерений п. По таблицам (см. прил. XII),

зная п и задавшись доверительной вероятностью |3, можно найти число г

, где

= 2(1 — Р). Если окажется, что г > г^, то это укажет, что х

следует исклю-

чить из ряда измерений. Так, например, в задаче 2.34 для х

= Хд »=57°23'48"

находим г = 3,3/2,5 = 1,32 (т = У 72,9 : 12). По вероятности 0 =• 0,95 (<? =

= 10%) и п = 12 из таблиц прил. XII находим г

= 2,387. Так как г < г

, то

измерение х

нельзя признать резко выделяющимся.

§ 21. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ И УРАВНЕНИЯ

РЕГРЕССИИ НА ОСНОВЕ ОПЫТНЫХ ДАННЫХ

Приведенные в § 12 формулы для вычисления коэффициента кор-

реляции редко применимы на практике, так как нужно знать матема-

тические ожидания и стандарты случайных величин X и V. На прак-

тике имеем пары наблюдений

Математическое ожидание в формуле (1.97) заменяют средним ариф-

метическим. При этом для несмещенной оценки коэффициента корре-

ляции получают формулу

XI XI Х

... Х

У1 Ш Уп

2 (*« — *) (у* — У)

Г* =

(п- \)т

(2.75)

= </< — У-

Очевидно, то же значение получим по формуле

* = ^— *)(уг — у) ,

(2.75')

101

Возникает вопрос, с какой надежностью вычисляется само значение

коэффициента корреляции и при каком минимальном абсолютном

его значении можно считать связь существующей, и наоборот. Воз-

никает, таким образом, необходимость оценки надежности коэффи-

циента корреляции.

Известный ученый, статистик В. И. Романовский рекомендует

при числе измерений п > 50 пр именять формулу для среднего квадра-

тического отклонения коэффициента корреляции

о,»(1 — г*)/У~п. (2.76)

Связь считается установленной, если выполняется условие

| г | > Зо

. (2.77)

Наименьшая величина коэффициента корреляции гш!п» удовлет-

воряющего условию (2.77) в зависимости от числа измерений п, вы-

числяется по формуле

Гш.п = (К^Тзе - уТ)/6. (2.78)

Для оценки надежности коэффициента корреляции при л < 50

пользуются специальной функцией, так называемым критерием Фи-

шера

= ^-{1п(1 +г)-1п(1-г)}, (2.79)

которая подчиняется закону нормального распределения. Стандарт

величины г вычисляется по формуле

(2.80)

Значения величины г по полученным из опыта значениям коэффи-

циента корреляции г могут быть вычислены непосредственно по фор-

муле (2.79) или по таблицам, приведенным в прил. VII. Уравнение

регрессии получает вид

У = У + г (х — Р), (2.81)

— ТП . —V

х = х + г^-(у — у). (2.82)

Шу

Среднее квадратическое отклонение коэффициентов регрессии

при большом п вычисляется по формуле

Шу, Г

,а ш / 1

= — 1 / —-; =— Л/

——

•

(2.83)

х V

*'« т

у п — 3

2.42. В табл. 18 приведены расстояния О, измеренные светодальномером

СВВ-1, и ошибки |Д| этих измерений. По данным таблицы вычислить коэффици-

ент корреляции, коэффициент регрессии, оценить их точность с вероятностью

не менее 0,90 и составить уравнение регрессии.

102

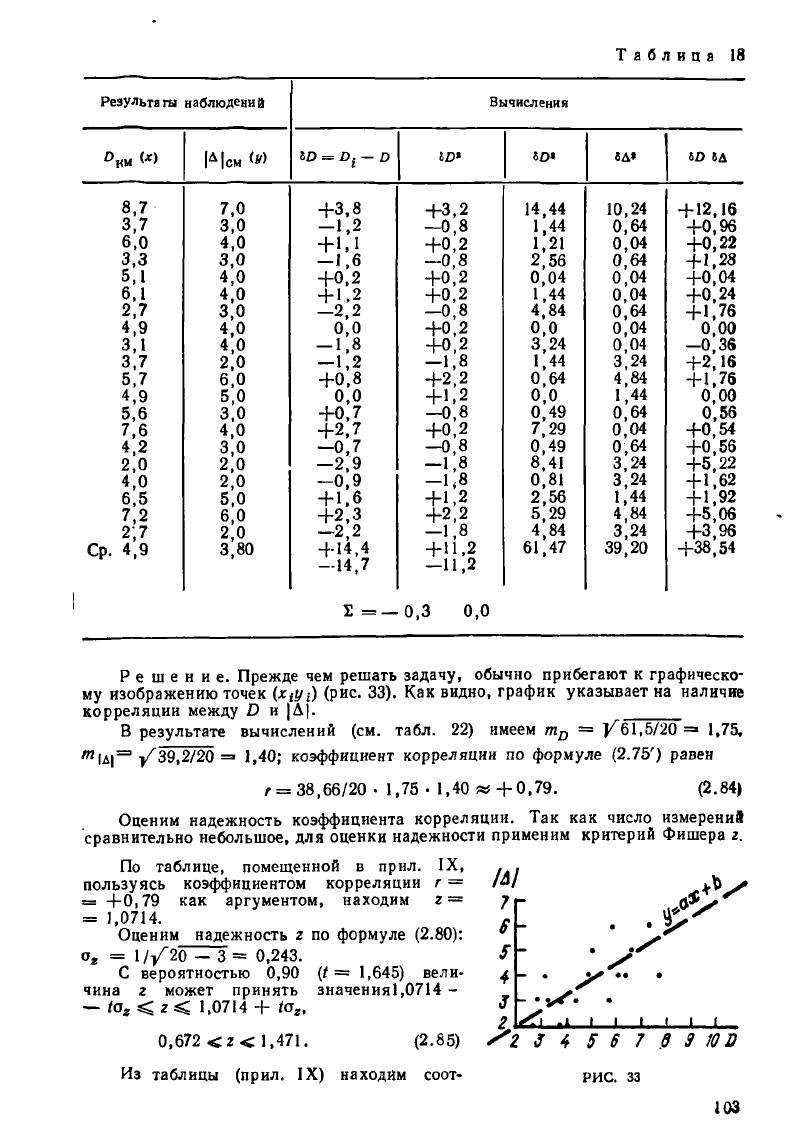
Таблица 29

Результат наблюдений

Нем <*>

Вычисления

80 = О.

—

й «Д»

«О !Д

7,0

3,0

4,0

3,0

4,0

3,0

4,0

2.0

6,0

5,0

3,0

4,0

3,0

2,0

5,0

6,0

2,0

3,80

+3,8

-1,2

+1,1

-1,6

+0,2

+ 1,2

-2,2

0,0

-1,8

-1,2

+0,8

0,0

+0,7

+2,7

-0,7

-2,9

-0,9

+ 1,6

+2,3

+ 14,4

-14,7

+3,2

-0,8

+0,2

-0,8

+0,2

—0,8

+0,2

—1,8

+2,2

+1,2

-0,8

+0,2

-0,8

+1,2

+2,2

-1,8

+ 11,2

-11,2

14,44

1,44

2,56

0,04

1,44

4,84

0,0

3,24

1,44

0,64

0,0

0,49

7,29

0,49

8,41

0,81

2,56

5,29

4,84

61.47

10,24

0,64

0,04

0,64

0,04

0,64

0,04

3,24

4,84

1,44

0,64

0,04

0,64

3,24

1,44

4,84

3,24

39.20

+12,16

+0,96

+0,22

+1,28

+0,04

+0,24

+1,76

0,00

-0,38

+2,16

+1,76

0,00

0,56

+0,54

+0,56

+5,22

+1.62

+1,92

+5,06

+3,96

+38,54

2 = — 0,3 0,0

Решение. Прежде чем решать задачу, обычно прибегают к графическо-

му изображению точек (х

{

) (рис. 33). Как видно, график указывает на наличие

корреляции между Г> и |Д|.

В результате вычислений (см. табл. 22) имеем т

= /61,5/20 = 1,75,

\ь\

' 39,2/20 = 1,40; коэффициент корреляции по формуле (2.75') равен

г =38,66/20 • 1,75 • 1,40 « +0,79. (2.84)

Оценим надежность коэффициента корреляции. Так как число измерений

сравнительно небольшое, для оценки надежности применим критерий Фишера г.

По таблице, помещенной в прил. IX,

пользуясь коэффициентом корреляции г =

= +0,79 как аргументом, находим г =

= 1,0714.

Оценим надежность г по формуле (2.80):

//20 — 3 = 0,243.

С вероятностью 0,90 (I = 1,645) вели-

чина г может принять значения1,0714 -

— Ю

< 1,0714 + {а

0,672 <г < 1,471. (2.85)

Из таблицы (прил. IX) находим соот-

103

/л!

• • ' • 1_

/2345 6 7 0 9

РИС. 33