Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

наличие действительной зависимости. Указанные задачи носят назва-

ние «задачи проверки правдоподобия гипотез».

3. Часто на практике не возникает вопрос определения закона рас-

пределения, а требуется по экспериментальным данным найти «наи-

лучшие» оценки для неизвестных параметров. С этой задачей связана

задача оценки точности этих «наилучших» значений.

Результаты наблюдений л-

, х

,..., х

случайной величины

X называются выборкой из генеральной совокупности (из всевоз-

можных значений случайной величины X).

Выборка называется повторной, если ее элементы независимы (на-

пример, номер вынутого из урны шара, если вынутый шар возвра-

щается обратно), и бесповторной, если ее элементы зависимы (на-

пример, если шар обратно в урну не возвращается).

Представительной (репрезентативной) называют выборку, если ее

элементы выбраны случайно, наугад. С целью изучения того или

иного явления выборка обязательно должна быть представительной

(например, если анализируется качество готовой продукции завода,

то изделия должны быть отобраны случайным образом, а не предста-

влены лучшие образцы).

При большом п выборка оформляется в виде статистического ряда

(вспомните ряд распределения). При этом весь диапазон наблюденных

значений х делится на интервалы («разряды») и подсчитывается коли-

чество значений, приходящееся на каждый разряд. Для каждого раз-

ряда вычисляется частость <2

(

= —. Статистический ряд имеет сле-

дующий вид:

Разряды ^ х

1г

; х

, х

; ...; х

!+1

\ ...; х

т.[ т

... пц ... т

О/ <Э

••• Як

Число разрядов к выбирается порядка 10—20, а их длины, как

правило, одинаковыми и такими, чтобы т

было не менее 5.

Для определения числа равных интервалов к, на которые следует

разбить весь диапазон значений х

, можно воспользоваться формулой

к = 1о§

гг + 1, при этом следует учитывать, что число интервалов

должно быть не меньше 8—10 и не больше 40, а п 50.

Статистический ряд часто оформляется в виде так называемой

гистограммы (по оси абсцисс откладываются разряды и на каждом

из разрядов как на основании строится прямоугольник, площадь

которого равна (2*, высота прямоугольника Н

{

= —— ). При

!+1

равных длинах разрядов Н{ пропорциональна С}^ Следует заметить,

что 2 Сг = 1-

(-1

Пример. Произведено 500 измерений некоторой величины. Результаты

измерений (в сантиметрах) сведены в статистический ряд

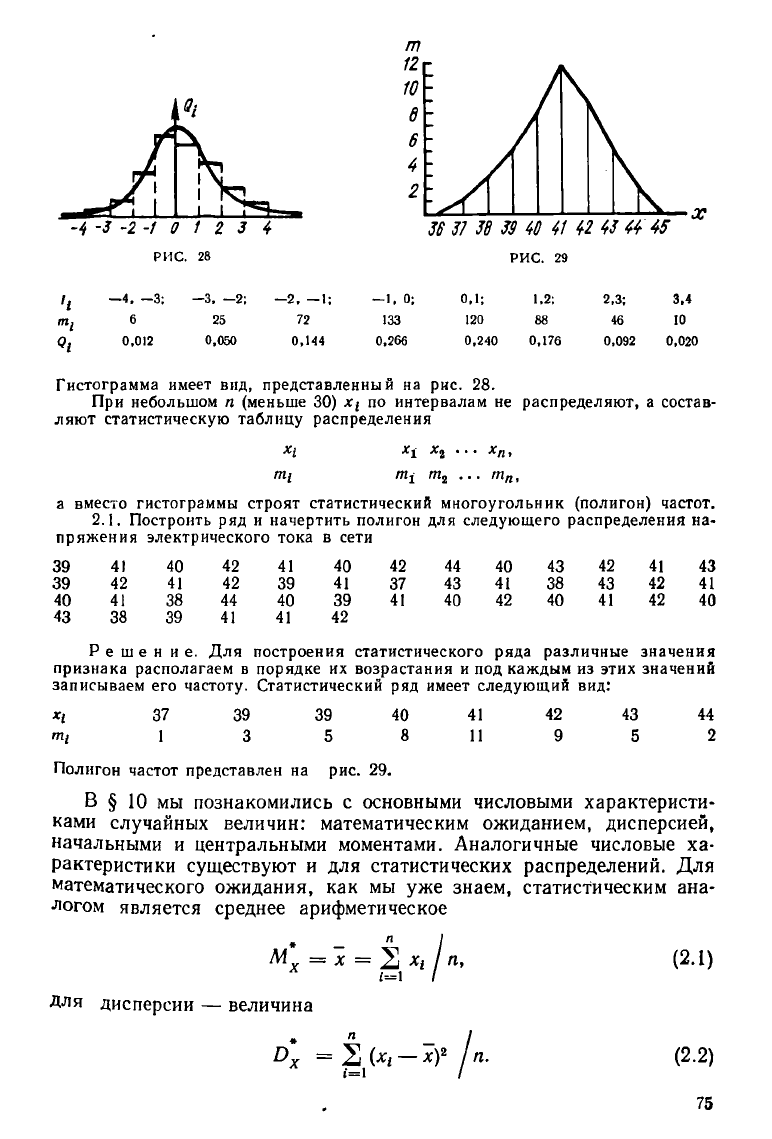
—4,-3; -3,-2; -2,-1; —1.0; 0,1; 1,2; 2,3; 3,4

Т^ 6 25 72 133 120 88 46 10

0,012 0,050 0,144 0,266 0,240 0,176 0,092 0,020

Гистограмма имеет вид, представленный на рис. 28.

При небольшом п (меньше 30) х

по интервалам не распределяют, а состав-

ляют статистическую таблицу распределения

XI х± х

• •

Ш1 т

... т

а вместо гистограммы строят статистический многоугольник (полигон) частот.

2.1. Построить ряд и начертить полигон для следующего распределения на-

пряжения электрического тока в сети

42 41

42 44

40 43

42 41

39 42

37 43

41 38

42 41

41 38 44

41 42

38 39 41 41

Решение. Для построения статистического ряда различные значения

признака располагаем в порядке их возрастания и под каждым из этих значений

записываем его частоту. Статистический ряд имеет следующий вид:

37 39 39 40 41 42 43 44

т, 1 3 5 8 11 9 5 2

Полигон частот представлен на рис. 29.

В § 10 мы познакомились с основными числовыми характеристи-

ками случайных величин: математическим ожиданием, дисперсией,

начальными и центральными моментами. Аналогичные числовые ха-

рактеристики существуют и для статистических распределений. Для

математического ожидания, как мы уже знаем, статистическим ана-

логом является среднее арифметическое

=х = ^х

1п, (2.1)

Для дисперсии — величина

=1,(х,-х)

П. (2.2)

1 = 1 /

Для статистических начальных и центральных моментов — соответ-

ственно

(2.3)

(2.4)

С = 2 х\ / П]

^ = 2 (*,— *)

/п.

Как видим, в этих формулах везде вместо математического ожи-

дания фигурирует среднее арифметическое. Однако некоторые оцен-

ки являются смещенными (см. § 18). Так, несмещенной оценкой дис-

персии будет

=2(*,-*)

/("- 1).

г=1

(2.5)

а не величина (2.2).

Для интервального статистического ряда имеют место формулы

_ I к

а* = 2 Щ х\ / 2

/ 1=1

_ I к

и* - 2 щ (*, — ху 2 щ-

* <=1 I 1=1

(2.6)

(2.7)

Статистические моменты имеют те же свойства, что и теоретические

моменты.

2.2. Доказать, что

г»» » »

Х =

1 •

(2.8)

Доказательство. Раскрывая скобки в выражении (2.2), получим

л л

2 А 2*г

й* = -27'-=^— + 2? •

х п п

Учитывая выражения (2.1) и (2.3), находим

х =

. 2 . .2

= а

— * = а

—а! .

2.3. В табл. 3 приведены следующие величины наблюдаемых значений

признаков XI, у

[9].

Таблица 3

1 «1

1 "г

«1

—10

—8

— 1

+ 10

+55

+20

+62

—2

+10

—2

б —1 15 — 11

—10

+22

+ 12 +28

—16 —30

—8

(

Найти оценки для числовых характеристик М

, Му, й

, йу.

О т в

т: х = 0,5, у = 7,15.

Дисперсии определены по формуле (2.8)

= 85,2; = 530,8.

2.4. Найти выражение центрального момента (Лд через начальные моменты.

Ответ:

-3*Х + 2а;

. (2-9)

2.5. Доказать, что

^ = -4*1 + б*;

*' - За*

. (2.10)

2.6. Дано распределение признака X:

—2—10123

2 4 6 5 2 1

Найти асимметрию и эксцесс.

Решение. Сначала находим начальные моменты первого, второго,

третьего и четвертого порядков данного распределения по формуле (2.6) с по-

мощью табл. 4*.

Отсюда

= 4/20 = 0,2; а* = 34/20 = 1,7; а* - 28/20 = 1,4; а* = 154/20 = 7,7

и Ц2

= а

2 — а* = 1,7 — (0,2)

= 1,66

(Х* = а*з— За^4 + 2а|

= 1,4 — 3 • 0,2 • 1,7 + 2 • (0,2)' =0,40;

ц* = а*-4а;аз-6<х|

а* — За^ = 7,7 — 4 • 0,2 • 1,4 + 6 • (0,2)*= 6,17.

Тогда

5* = = ^з

^з

0.40

МО

^ '.

66 1

29 2

' '

* В прил. XIII.2 и XIII.3 приведены программы для калькулятора «Элект-

роника БЗ-21» вычисления моментов а* («=1,2, 3, 4) по формулам (2.3) и

(2.6).

Таблица 4

{

х.

{

т,

Х[

—2

2 —4 8

—16

—1 4

—4

0 6 0 0 0

5 5 5

5 5

3 9

Сумма

4 34

151

5 = — -3= — — 3=/ 3 = 0,77.

/(1.66)

2.7. Дано распределение признака X

Х, 2

3 4 5 6 7

2 6 8 5 3 1

Найти его асимметрию и эксцесс.

Ответ: 5* = 0,303; Е = —0,478.

§ 17. ОПРЕДЕЛЕНИЕ ЗАКОНА РАСПРЕДЕЛЕНИЯ НА ОСНОВЕ ОПЫТНЫХ

ДАННЫХ (ВЫРАВНИВАНИЕ СТАТИСТИЧЕСКИХ РЯДОВ)

Задача выравнивания заключается в том, чтобы подобрать теорети-

ческую плавную кривую распределения (<р(л:)), наилучшим образом]

описывающую данное статистическое распределение. Как правило,

вид теоретической кривой выбирается заранее из существа задачи, а

в некоторых случаях по внешнему виду гистограммы. Поэтому задача

переходит в задачу выбора параметров распределения.

Например, взгляд на гистограмму (см. рис. 28) заставляет пред-

полагать нормальное распределение

"И

<Р

(*)= —

. (2.11)

о у 2л

Тогда задача сводится к рациональному выбору параметров аист

в формуле (2.11). Один из методов (метод моментов) заключается в под-

боре параметров таким образом, чтобы несколько важнейших число-

вых характеристик были равны соответствующим статистическим ха-

рактеристикам

а = М* [X]; о = У У* [-<] •

Вычислим а и ст по приближенным формулам (см. пример на

стр. 76)

а = М*\Х\ = =0,168,

_ *=1

где х

— среднее разряда, и

где «*= 2 ^<3, = 2,126,

1=1

О* [X] = 2,126 — 0,028 = 2,098.

Итак, а = 0,168 и о = 1,448.

Напишем выражение нормального закона

(х—0,168)»

Ф (*) Ц— е

УЪГ 1.44в

Пользуясь таблицами прил. II, вычислим Ф(Х

{

) = р

XI —4 —3 —2 —1 0 1 2 3 4

Р1 0,004 0,025 0,090 0,199 0,274 0,234 0,124 0,041 0,008

= 0,999» I

на границах разрядов и построим выравнивающую кривую (см.

рис. 28).

Рассмотрим вопрос, связанный с проверкой правдоподобия гипо-

тез, а именно вопрос о согласованности теоретического и статистиче-

ского распределения. К. Пирсон в качестве меры расхождения между

и <2г принял величину х

у (т-пр,)* .

(2Л2)

^^ ПР1

1=1

Распределение х

зависит от параметра г, называемого «числом

степеней свободы», который равен числу разрядов к без числа связей,

накладываемых на частоты; например, для нормального закона этих

связей 3,

2<Э*=1> 2 *«<?! = О. = ст

1=1 (=1 1=1

4 Х

так что г — к — 3.

Число т

в каждом интервале не должно быть меньше 5 — 10.

В противном случае интервалы приходится объединять.

Для распределения у

составлена таблица (см. прил. VI). Поль-

зуясь этой таблицей, можно для каждого значения у

и числа сте-

пеней свободы г найти вероятность Р того, что величина, распределен-

ная по закону х

. превзойдет это значение (или Р есть вероятность

того, что за счет чисто случайных причин мера расхождения (2.12)

будет не меньше, чем фактически вычисленная у

). Если эта вероят-

ность мала, то результат опыта следует считать противоречащим ги-

потезе о том, что закон распределения X есть ф(я), если велика, то

гипотезу следует считать правдоподобной. На практике часто счи-

тают критическим значением вероятности Р = 0,1.

Вычислим х

для нашего примера. Вероятность попадания в ин-

тервал /, определяем по формуле (1.67)

1 Г

-0,168 4 _

I XI 0,168 XI

' 2 1 \ 1,448 ) I 1,448 )}

в результате чего получим

Л —4; —3 —3;—2 —2; —1 —1; 0 0; 1 1; 2 2; 3 3; 4

Рг 0,0124 0,0524 0,1424 0,2444 0,2638 0,1810 0,0764 0,0210

ПР1 —6,2 26,2 71,2 122,2 131,8 90,5 38,2 10,5

Щ 6 25 72 133 120 88 46 10

г =

•3 = 5.

По таблице прил. VI находим р = 0,56 > 0,10.

Следовательно, гипотезу/6 том, что величина X подчиняется нор-

мальному закону, можно считать правдоподобной*.

Для проверки гипотезы о согласованности результатов экспери-

мента с предполагаемы^ законом распределения существуют и другие

критерии, например А. Н. Колмогорова, который здесь не приводит-

ся.

При исследовании выборки на нормальный закон распределения

существует и ряд приближенных критериев. Так, в случае нормаль-

ного закона распределения, как мы уже знаем (см. § 11), между

вероятным отклонением г и стандартом о существует точная зави-

симость

г = 0,675а. (2.13)

По результатам выборки величина г оценивается вероятной ошиб-

кой (эмпирическим значением г*) при расположении всех значений

{

в порядке возрастания или убывания их абсолютных величин. Тогда

г* будет находиться в середине такого ряда. Например, если х

{

—

ошибки измерений Д<, то г* = |Д

(

|, г = (п + 1)/2 при нечетном п

или г* = (Д, — Л

,)/2, ' = "/2 при п четном.

При нормальном законе распределения между средним отклоне-

нием V к о существует зависимость

о = 1,253V. (2.14)

Оценку для V вычисляют по формуле

= /п

или, если А/ — ошибки измерений,

2 И*

т.

1—\

Заменим стандарт ст его оценкой т = К[Д

]М; будем иметь вме-

сто (2.13) и (2.14) приближенные зависимости

г*» 0,67т, (2.15)

т*«1,25*. (2.16)

которые будут тем точнее,чем ближе закон распределения к нормаль-

ному. К сожалению, указать границы изменения коэффициентов

* Заметим, что если р яв 1, это еще не означает, что согласие результатов

эксперимента с теоретической кривой очень хорошее. Наоборот, это указывает

скорее на «подтасовку» экспериментальных данных.

во

= 0,67 и к

= 1,25, при которых закон распределения можно счи-

тать нормальным, не удается иэ-за сложности закона распределения

оценок г* и т*. Известно также, что для нормального закона распре-

деления скошенность 5

(асимметрия) и эксцесс Е (островершинность)

кривой распределения равны нулю. Однако эмпирические значения

скошенности 5

и эксцесса Е (см. § 16), вообще говоря, не равны нулю.

Считается, что отклонение от нуля этих величин не противоречит ги-

потезе нормальности кривой распределения, если выполняются не-

равенства*

(2.17)

| Е | < 5 УЖ, (2.18)

где дисперсии

<"-'> » —; Р

= ^(*-2)(п-3)

(л+1)(я + 3) я (л+!)»(я+3)(л+5) л '

а п — объем выборки.

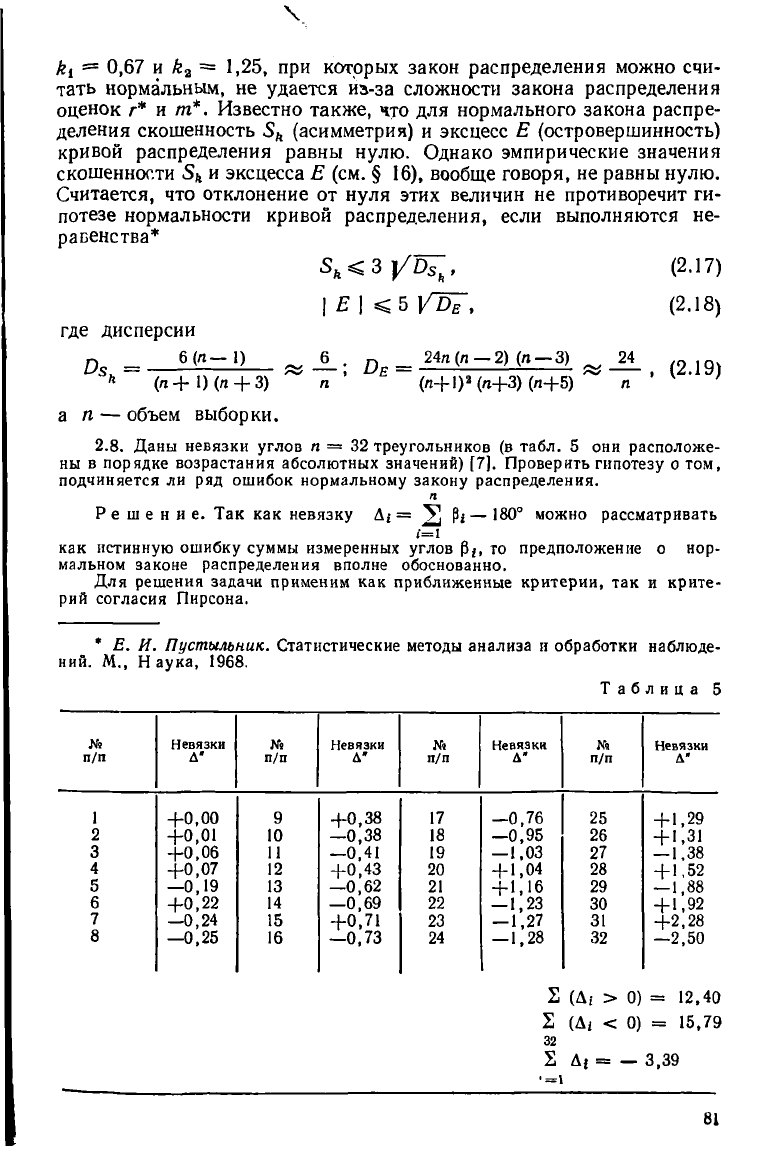
2.8. Даны невязки углов п = 32 треугольников (в табл. 5 они расположе-

ны в порядке возрастания абсолютных значений) [7]. Проверить гипотезу о том,

подчиняется ли ряд ошибок нормальному закону распределения.

Решение. Так как невязку Д{ = 2 — 180" можно рассматривать

как истинную ошибку суммы измеренных углов то предположение о нор-

мальном законе распределения вполне обоснованно.

Для решения задачи применим как приближенные критерии, так и крите-

рий согласия Пирсона.

* Е. И. Пустыльник. Статистические методы анализа и обработки наблюде-

ний. М., Н аука, 1968.

Таблица 5

№

Невязки

№ Невязки

№

Невязки

№

Невязки

п/п

Д*

п/п Д' п/п Д"

п/п

Д"

+0,00

9 +0,38

-0,76

25 +1,29

+0,01 10

—0,38 18

-0,95 26

+ 1,31

+0,06 11

—0,41

19 —1,03 27

— 1,38

+0,07

+0,43 20

+ 1,04

+ 1,52

5 —0,19

—0,62

+1,16

—1,88

+0,22

—0,69 22

— 1,23

+ 1,92

—0,24

15 +0,71

-1,27 31 +2,28

—0,25 16 —0,73

24 — 1,28

32 —2,50

2 (А* > 0) = 12,40

2 (Д

< 0) = 15,79

Е Д| = — 3,39

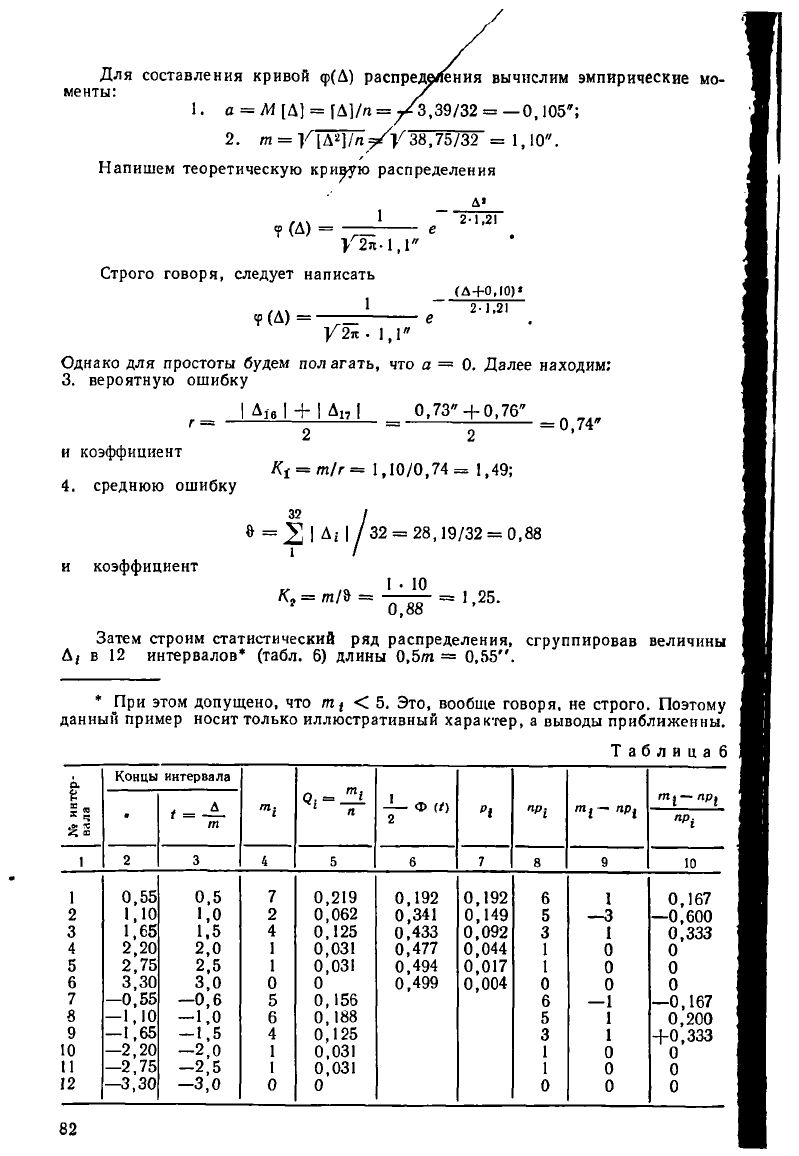
Для составления кривой ер(Д) распред"

менты:

1. а = М [Д] = [Д]/п =^3,39/32 = — 0,105";

2. т = У [Д2]/п у/V 38,75/32 = 1,10".

Напишем теоретическую кривую распределения

— А'

/л\

21,21

? (А) = е

\2к-1,1"

Строго говоря, следует написать

(А+0.Ю)«

/ач

21,21

9 (Л) = —— е

У2я • 1,1"

Однако для простоты будем пол агать, что д = 0. Далее находим:

3. вероятную ошибку

г=

I Л

| + | А» [ _ 0,73"+0,76"

2 2

и коэффициент

К{ = т/г = 1,10/0,74= 1,49;

4. среднюю ошибку

32 /

& = 2 I А; I! 32 = 28,19/32 = 0,*

_ . .88

1 /

и коэффициент

Затем строим статистический ряд распределения, сгруппировав величины

в 12 интервалов* (табл. 6) длины 0,5/л = 0,55".

* При этом допущено, что т

(

< 5. Это, вообще говоря, не строго. Поэтому

данный пример носит только иллюстративный характер, а выводы приближенны.

Таблица 6

о.

Концы интервала

О. =

1Г

л.

•

(--Л.

О. =

1Г

— Ф (О

пр

—

пр

1 2

0,55

0,5

0,219

0,192

0,167

1,10

1,0

0,062

0,341

0,149 5

—3

—0,600

1,65

1.5

0,125

0,433

0,092 3

0,333

4 2,20 2,0 1

0,031

0,477

0,044

2,75

2,5 1

0,031

0,494

0,017

3,30

3,0

0 0

0,499

0,004

0 0

—0,55

-0,6

0,156

0,499

0,004

—1 —0,167

8 —1,10

—1,0 6

0,188

0,200

9 —1,65

— 1,5

0,125

3 1

+0,333

—2,20

—2,0

0,031 1

11 —2,75

-2,5 1

0,031 1

—3,30 -3,0

В графе 6 таблицы вычислены вероятности попадания ошибки Д

в интер-

вал от 0 до а в графе 7— вероятности попадания в 1-е интервалы. Так как рас-

пределение симметричное, то эти вероятности выписаны только для интервалов,

расположенных справа от 0. В графе 8 вычислено теоретическое число ошибок,

попавших в 1-й' интервал (также одинаковое для положительных и отрицатель-

ных интервалов). В графе 9 вычислены разности между фактическими и теорети-

ческими числами ошибок «-го интервала. Методом накопления на калькуляторе

«Электроника БЗ-21» вычислена величина

3,0.

^ ПР1

1=1

По таблицам прил. VI при числе степеней свободы г = 12 — 2 = 10 (число

связей, накладываемых на частоты, здесь принято равным двум, а не трем,

так как при вычислениях мы полагали, что = 0) находим для х

2 =

3 вероят-

ность р = 0,981. Для вычисления асимметрии и эксцесса находим начальные

моменты:

а* = — 0,106; о* = —0,137;

<4=1,211; 04 = 3,772.

Вычисления выполнены по программе, срставленной для калькулятора

«Электроника БЗ-21» (см. прил. XIII.2). Согласно формулам (2.9) и (2.10) далее

получаем

,4 = 0,246; (V )

= 1,313;

(< = 4.287; (/=1,44;

0,246 4,287

; = ТЖ=°'

,87:

^ = ^-3 =-0,023,

а согласно формуле (2.19) !>„• = 0,171 и Г>

.= 0,474. Неравенства (2.17) и

с.

(2.18) примут вид 0,187 < 1,240 и 0,023 < 3,442.

Для иллюстрации применения формулы (2.6) вычислим асимметрию и экс-

цесс по интервальному ряду, полагая Х{ равным средним значениям интервалов.

Вычисления располагаем в табл. 7.

Таблица 7

Интервалы 1

~з

Интервалы 1

1~г

ш, Х(

т, х

(

1 0,27

7 1,89

0,51

0,14

0,04

0,82 2

1,64

1,34

1,10

0,90

3 1,38 4 5,52

7,62

10,52 14,52

1,92

3,69

7,08

13,59

2,48

6,15

15,25

37,82

3,02

0 0 0 0 0

—0,27 5 — 1,35

0,36

—0,10 0,03

—0,82 6 —4.92

4,03

—3,30

2,71

9 —1,38

4 —5,52

7,62

—10,52

14,52

—1,92

— 1,92

3,69

—7,08 13,59

11 —2,48

—2,48 6,15

-15,25

37,82

—3,04

-2,74 41,18

—2,16

135,54