Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

Аналогично

ФЛу)

= у) с!х

(1.80)

Формулы (1.77), (1.79) и (1.80) позволяют найти частные законь

распределения, зная совместный закон.

Однако обратную задачу — установить закон совместного распре^

деления, зная только частные законы, можно решить не всегда. Лишь|

в случае, когда случайные величины х и у независимы, можно напи^

сать

ф(*. 0) = Фх (*) Ф« (0)

(1.81)

(сравните с теоремой умножения для независимых событий).

Случайная величина у называется независимой от случайной ве

личины х, если закон распределения величины у не зависит от тога

какое значение приняла величина х.

Аналогично условной вероятности Р(А

/А

) для событий вводятся

так называемые условные плотности распределения: [(у/х) — пло^

ность распределения у при условии, что случайная величина х приня

ла значение х, и {(х/у) — плотность распределения х при условии, чт

случайная величина у приняла значение у.

Если условные плотности (условные законы) распределения из

вестны, то плотность совместного распределения

(1.82)1

Ф (х, у) = Ф

(Х) Ф {у/х)

или

Ф(*»

У)

Ч>г(у)Ч>(х/у).

(1-83

Сравнивая выражения (1.82) и (1.83) с (1.81) приходим к математй

ческому условию независимости

Ф [у/х) = Ф.

(у)

(1-

или

(х/у)

= ф

(*).

(1.8

Здесь имеется в виду так называемая вероятностная (статисти*

екая) зависимость. Вообще, различают два вида зависимостей

функциональную и вероятностную.

Функциональной зависимостью между дву!

величинами X и У называют такую зависимость, при которой ка!

дому значению X соответствуют значения V, которые можно точ^

— 4

указать (например, у = ух, V = -д-яЯ и т. д.)

Вероятностной зависимостью между двумя

личинами X и У называют такую зависимость, при которой каждое

значению л:соответствует распределением/, изменяющееся с изменение

х (условное распределение). Вероятностная зависимость между сл

чайными величинами на практике встречается очень часто. Пример

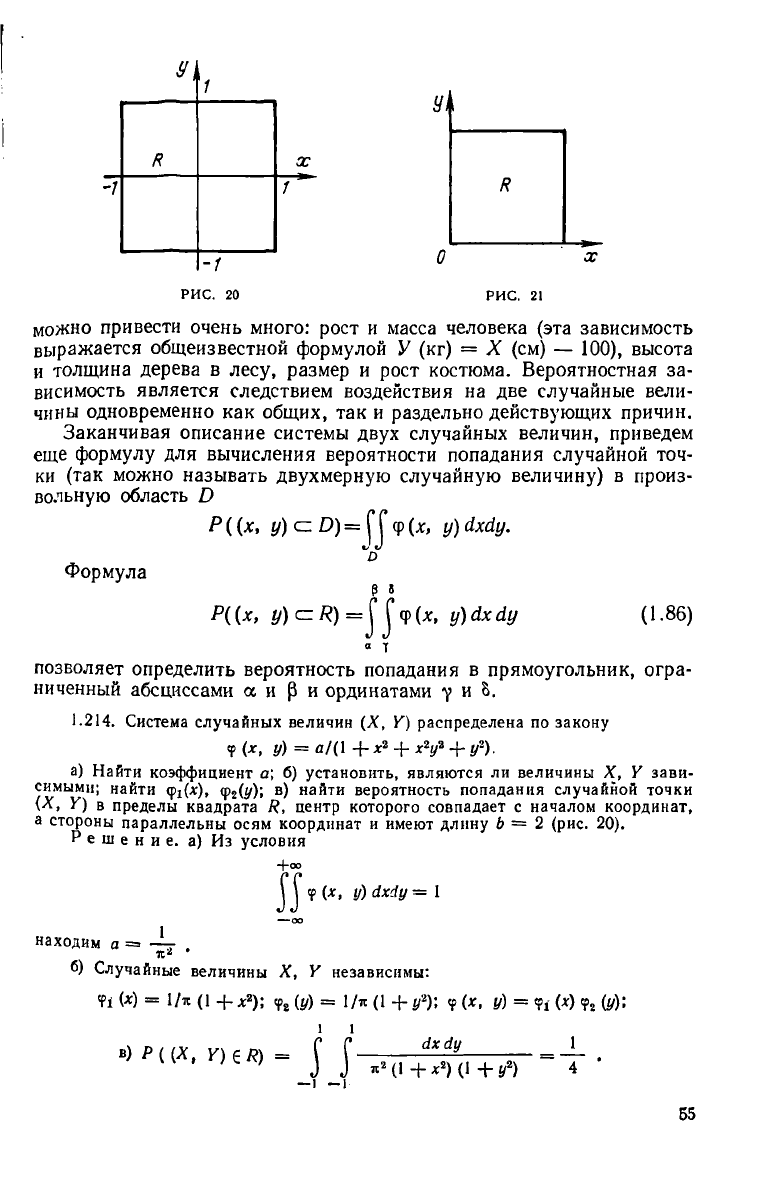
РИС. 20 РИС. 21

можно привести очень много: рост и масса человека (эта зависимость

выражается общеизвестной формулой У (кг) = X (см) — 100), высота

и толщина дерева в лесу, размер и рост костюма. Вероятностная за-

висимость является следствием воздействия на две случайные вели-

чины одновременно как общих, так и раздельно действующих причин.

Заканчивая описание системы двух случайных величин, приведем

еще формулу для вычисления вероятности попадания случайной точ-

ки (так можно называть двухмерную случайную величину) в произ-

вольную область й

Р ((л:, у) <= 0)=

ср

(х, у) йхйу.

"о

Формула

9 8

Р( (х, у)

Я) = 11Ф (х, у) йхЛу (1.86)

« т

позволяет определить вероятность попадания в прямоугольник, огра-

ниченный абсциссами а и Р и ординатами -у и В.

1.214. Система случайных величин (X, V) распределена по закону

?(*, у) = а/(1 + +

а) Найти коэффициент а; б) установить, являются ли величины X, V зави-

симыми; найти <рх(*), фг(у);

) найти вероятность попадания случайной точки

(X, V) в пределы квадрата Я, центр которого совпадает с началом координат,

а стороны параллельны осям координат и имеют длину 6=2 (рис. 20).

Решение, а) Из условия

+°о

<е

(*. у)

<1хс1у

= 1

—ОО

находим а = —•

1С

б) Случайные величины X, V независимы:

(*) = 1/* (1 + х*у,

Чг

(у) = 1/« (1 + у*); ? (*, у) =

<?,

(*)

?г

(у);

в)Р((Л, т*)= ( Г—.Л..

^ ^ с+*

> о+у )

—1 —1

1.215. Найти вероятность попадания случайной точки {х, у) в прямоуголь-

ник Я, ограниченный прямыми х = п/6, х == я/2, у = п/4, у = л/3, если

/Ч*, I/) = 81П

51Ш/ (0 X

^ У ^

)

Решение: Находим

ЗУ{х. у)

? (х, Ч)= т—т =

СОЗ ДГС05

ох оу

и далее:

тс/2

я/3 я/2 к/3

Р ((X, У) < я) = ^ ^ соз * соз у Ах йу = со$ хёх ^ соз уйу=

я/6 1/4

*/2

я/3

ч/б

= (1-0,5)

к/4

я/6 я/4

Кз у!" \

Уз- КГ

:0,08.

1.216. Система случайных величин (X, У) распределена с постоянной плот-|

ностью внутри квадрата Я со стороной 1 (рис. 21). Написать выражение плотнос-

ти и функции распределения <р(ж, у), Р(х, у). Построить функцию распределения

системы. Написать выражения ф](*), фаО/)- Определить, являются ли случайные!

величины (X, У) независимыми или зависимыми.

Ответ:

<р

(*, «/)=

1 при (х, у) 6Я,

<Р

(*. У)=

91 (

) =

0 » (х, у) 6 Я.

0 при х < 0 или у < 0,

ху » 0 < х < 1 и 0<г/<1,

х » 0 < х < 1 » у > 1,

у » * > 1 » 0 <

«/<

1 » * > 1 » у > 1.

1 при * 6(0,1),

0 » (0.1),

1 при 1/6(0,1),

0 » ^6(0,1).

Случайные величины (X, У) независимы, так как ф (х, у) =» ф1(*)ф

(</)]

1.217. Дана плотность совместного распределения

У)

(4 + *

) (9 + у

) '

Найти: а) величину с; б) Р(х, у).

Ответ! а) с = 6/я

, б) Р(х, у) = ^ агс18 ~ + | X

^ агс1

^ + 4-) .

1.218. Двухмерная случайная величина задана поверхностью распределе-

ния

<Р(*. У)=

Найти ч>1(*) и ф

((/); зависимы ли *, у?

Ответ:

6я

при

* т

2-1.

Кэ —*

при |х| <3,

— V у

при \у\ < 2,-

&) =

2я

1 0 »

> 2.

Величины х и у зависимы.

1.219. Двухмерная случайная величина (х, у) задана дифференциальной

функцией

? (*. У)=

ЛГ

при

ж?

+ у? < г

» *

+ {/

>Г

Найти условные плотности распределения.

Ответ:

<Р

(*/</) = { 2 V Г

—!/

?&/*)={ 2 Кг

— *

при

I XI

< V Г

— у

» 1*1 > V

Г*

- у\

при \у\ < Кг-—*

» \у\ > К г

—*

1.220. Случайные величины X и У независимы и распределены по законам,

заданным в виде частных кривых распределения

(*) =

У~2ка

(х-М

)•

2з»

(нормальный закон) с параметрами М

=• 0; о = и

У 2

Ъ (У) =

Р-а

(равномерный закон) в интервале (0,1).

написать плотность совместного распределения.

Ответ:

У>

О при у < О,

а х

Р(х, У)= р

(X) р

(и) =\уР(хУ2 ) » О <у<1,

р(хУ'Г) » (/>1.

РИС. 22

1.221. Двухмерная случайная величина распределена в первой четверти кон

ординатной плоскости (0 х < +оо, 0 ^ у < +°о) с плотностью вероятности

<р(ху) = Ае~'~

. Найти Р{х, у) и вероятность попадания в прямоугольник, изо-)

Сраженный на рис. 22.

Указание. Коэффициент А найти из условия

У А<?(х, у)Лхйу= 1.

о о

Ответ: /4=1, Р(х, у) = (1 — е~

)(1 — е~У).

§ 13. КОРРЕЛЯЦИЯ. КОРРЕЛЯЦИОННЫЙ МОМЕНТ И КОЭФФИЦИЕНТ

КОРРЕЛЯЦИИ. УРАВНЕНИЕ РЕГРЕССИИ

В § 12 мы познакомились с понятием вероятностной зависимост

и определили ее как такую зависимость, когда с изменением случай-

ной величины X изменяется закон распределения случайной величины

У. Как мы уже знаем, закон распределения, например, для непрерыв

ной случайной величины задается кривой распределения у(х). В за-

висимости от того, что изменяем в выражении у(х) — ее вид или

только некоторые числовые характеристики, — различают несколько

типов вероятностной зависимости. Одним из наиболее распространен-

ных типов такой зависимости является так называемая корреляцион-

ная зависимость, при которой с изменением х изменяется математиче

ское ожидание у (рис. 23, а и б). Оба рисунка иллюстрируют эту за-

висимость, причем в первом случае изменение Му происходит непрямо

линейно (криволинейная корреляция), а во втором — по закону пря-

мой линии (прямолинейная корреляция). Эту последнюю зависимость

РИС, 23

часто называют для краткости корреляцией. Если зависимость между

X и У будет установлена и выражена формулой, то ее можно исполь-

зовать для надлежащей организации и обработки результатов экспе-

римента, например, измерений.

Систему двух случайных величин, как и одну случайную величи-

)

кроме задания закона совместного распределения, определяют

еще числовыми характеристиками, так называемыми специальными

начальными и центральными моментами порядка 5,9,

8>?

= М[Х*, У*\ \ =М[(Х-М

)*(У-Л1

)*1. (1.87)

В частном случае, очевидно, имеем

«1.0 =

X >

"о.. =

У »

^2.0 = > ^0.2 = °У '

(1.88)

В теории корреляции важнейшее значение имеет центральный сме-

шанный момент второго порядка

1л

=М\(Х-М

)<у-М

)\, (1.89)

который называют корреляционным моментом и обозначают КХУ- Его

вычисляют по формулам

Кху= ^(Х

-М

)(у

-Му)р

ху

1=1

+00 +оо

КХУ

= ^ — М

)(у — М

)у(ху)йхйу

(1.90)

(1.91)

—оо —оо

соответственно для прерывных и непрерывных случайных величин.

Момент Кхт как раз и характеризует силу, тесноту корреляции.

Однако его значение зависит еще и от размерности случайных вели-

чин. Для того чтобы освободиться от последней, вычисляют так на-

зываемый коэффициент корреляции

г = К

у/а

X °У

(1.92)

который численно характеризует силу корреляции в чистом виде.

Коэффициент корреляции изменяется в пределах — 1 < г < 1.

Когда он равен +1 или —1, между х и у существует прямолинейная

зависимость (рис. 24. а и б) у = ах + Ь.

РИС. 24

РИС. 25

РИС. 26

В случае г<. О имеет место отрицательная корреляция! с умен

шением (увеличением) X величина У имеет тенденцию увеличивать

ся (уменьшаться); при г~> О говорят о положительной корреляции: с

уменьшением (увеличением) X величина У имеет тенденцию уменм

шаться (увеличиваться).

На рис. 25 показана положительная корреляция, причем в первом

случае она более тесная, чем во втором (/•) > г

), а на рис. 26 — от-

рицательная корреляция, более тесная также в первом случае.

Если случайные величины X и У независимы, то корреляционный}

момент Кхг — 0 (также с г

ху

= 0).

Две корреляционные случайные величины также и зависимы. Об-'

ратное утверждение не всегда имеет место, т. е. если две величины

зависимы, то они могут быть как коррелированными, так и некорре-

лированными.

В том, что две зависимые величины могут быть некоррелированны-

ми, легко убедиться на следующем примере.

Пусть поверхность распределения задана в виде

<р(ху)

= л внут-

ри эллипса + = 1 и ф(ху) = 0 вне его. Найдем корреляцион-

ный момент по формуле

КХУ

= — М

)(у—М

)ч(ху)с1х(1у.

Так как плотность распределения

_ 2

<М*)

— Кэ

— х*

внутри эллипса,

вне его

симметрична относительно оси оу, то М

= 0, аналогично М

= О,

ха

ак плотность

, . , К9 — о

внутри эллипса,

О вне его

симметрична относительно оси х.

Поэтому

+ СО

КХУ = ху Ф (ху) йх йу.

Учитывая, что [(ху) не содержит переменных, получим

Цхйхшу.

—оо —оо '

Внутренний интеграл равен 0 (подынтегральная функция нечетна,

пределы интегрирования симметричны относительно начала коорди-

нат). Следовательно, КХУ — 0, т. е. х и у некоррелированы, однако

зависимы, так как ф(ху) ф ф1(х)<р

(у)-

На практике часто встречаются двухмерные случайные величины,

распределение которых нормально. В этом случае

( к-М

(У - Му Р ^ (;к -М

)

(У

- Му

"X — "У

2 (1- г')

ф (ху) = а ехр

где а = \12ла

У^\—г

, а так называемая экспонента ехр с — е°.

При нормальном законе распределения из некоррелированности

следует и независимость х и у. В самом деле, пусть г

у = 0. Тогда

(ху)=

ехр

(х—М

)* (у — Му )»

т :

(*- м

(у - Му

Учъ а

что и означает независимость случайных величин х и у.

Таким образом, если две случайные величины подчинены нормаль-

ному закону распределения, то некоррелированность и независимость

понятия тождественны.

Корреляционную зависимость, кроме задания ее тесноты, необхо-

димо характеризовать формой.

Форма прямолинейной связи между X и У выражается в виде так

называемого уравнения регрессии У на X

у — М\У\ = (

— М [X])

(1.93)

или

у = М\У] +

9т

{

-М[Х\), (1.94)

где коэффициент

у/х

= г^- (1.95)

— коэффициент регрессии у на х. На рис. 25, 26 сплошные линии яв-

ляются уравнениями регрессии.

Существует уравнение регрессии х на у, имеющее вид

* = М[Х] + р

х1и

(у-М[У\),

где р

х/у

= г— .

ау

1.222. Доказать, что если случайные величины х и у независимы, то кор-

реляционный момент Кху ~ О-

Решение. Воспользуемся формулой (1.91). Имеем для независимых

величин

+ 00 +00

хг=

— Мх

Му

§(х —

х)Ч (*)

йх

—оо —оо

+оо

X ^(У—Му)ч(у)(1у. (1.96)

—оо

Но интегралы-сомножители в формуле (1.96) представляют собой центральные

моменты первого порядка, равные нулю. Поэтому Кху ~ 0.

1.223. Доказать, что корреляционный момент

ху

М[(х-М

){у-Му)\

(1.97)

можно представить в виде

*ху =

ХУ~

У (1-93)

Указание. Раскрыть скобки в выражении (1.97) и воспользоваться

свойствами математического ожидания.

1.224. Доказать, что если между величинами X и К имеет место функцио-

нальная зависимость вида у = ах + Ь, то коэффициент корреляции = 1.

Доказательство. Имеем Му = аМ

4- Ь.

Поэтому для корреляционного момента получим

ху

= М [(X — М

) (а +

— аМ

— Ь)] = аМ [(X — М

) (У — М

)] =

= аМ[(Х-М

)

] = а4 .

Дисперсия Оу •= а

(по свойствам дисперсии (1.39—1.40)), откуда а

= а

\а\з

(величина а взята по модулю, так как по определению стандарт-вели-

чина всегда положительная). Поэтому

ху

ас

а _ \ + 1 при а >0,

|а| з

/а| ( —

при а < 0.

1.225. Имеются три независимые случайные О

величины 2х, 2» и 2

с известными математическими

ожиданиями Л![2

(

] и с. к. о. Найти коэффи-

циент корреляции между функциями

Х = 2, + 2./, К = 2, + 2

;

написать уравнение регрессии у на х.

Решение. Имея в виду формулы (1.92)

и (1.98), находим, пользуясь свойствами матема-

тического ожидания (1.35),

ХУ = 2\ + 2

+ 2

;

м [ХК] = мг\ + мг,2, + мг^ + мг

* 00у

М [X] = М [2!-] + М [2

]; М[У\ = М [2А + М [2

];

М [X] М [У] = м\ - М

гх

г%

- м

2х

гг

- М

1г

2г

Поэтому К

ху

= М\ХУ] — М

= мг] — М\ = о|

(

на основании

(1.45). Следовательно, г

ху

= о| /а

• а

На основании свойства дисперсии для независимых величин имеем о

= о| + о| и Оу = о| + о|

. Поэтому

Если а

•= а

= о

2г

= а

, то

ХУ= °1/°Г К2"=+0-

В этом случае уравнение регрессии будет у = Му + 0,5(д; — М

1.226. Доказать, что коэффициент корреляции между двумя углами у

г/в» измеренными способом круговых приемов (рис. 27), равен г = —0,5. Объяс-

нить, что вызывает корреляцию этих углов. Построить уравнение регрессии у

на у

и у

на у

1.227. Плотность распределения двухмерной случайной величины задана

формулой

1 ~~ Г28

[(дс-2,г_ 1,2 (х

2) (у + 3) +

<*+

3>,]

Найти с. к. о. о

, о

^ коэффициент корреляции г

ху

Ответ: а

= У2.

1.228. Найти коэффициент корреляции и написать уравнение регрессии у

на у

если = х

у = — х

, а а

х<

= а

§ 14. ПОНЯТИЕ О МНОГОМЕРНОМ РАСПРЕДЕЛЕНИИ. КОРРЕЛЯЦИОННАЯ

МАТРИЦА

Обобщая понятие двухмерной случайной величины, говорят о со-

вокупности случайных величин Х

, ..., Х

, которую называют п-

мерным случайным вектором, а величины Х

{

— его случайными коор-