Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

У р 1

г)

Р&1/Л) =-|—з

— V р(А/Н

)

1=1

Аналогично

р (Н

/А) = ; р (Н

/А) = - Ц

а +

с + а

+ 1

а +Ь

с + а

+ 1

1.114. В группе из 10 студентов, пришедших на экзамен, 3 подготовленных

отлично, 4 — хорошо, 2 — посредственно и 1 — плохо. В экзаменационных би-

летах имеется 20 вопросов. Отлично подготовленный студент может ответить на

все 20 вопросов, хорошо подготовленный — на 16, посредственно — на 10, пло-

хо — на 5. Вызванный наугад студент ответил на три произвольно заданных во-

проса. Найти вероятность того, что этот студент подготовлен: а) отлично; б) пло-

хо.

О т в е т: а) р^Н^А) да 0,58; б) р(#«/Л) да 0,002.

1.115. Два охотника одновременно стреляют в цель. Известно, что вероят-

ность попадания у первого охотника равна 0,2, а у второго — 0,6. В результате

первого залпа оказалось одно попадание в цель. Чему равна вероятность того,

что промахнулся первый охотник?

Ответ: 6/7.

§ 6. МНОГОКРАТНЫЕ ПОВТОРНЫЕ ИСПЫТАНИЯ. ФОРМУЛА

БЕРНУЛЛИ

Если необходимо определить вероятность того, что при независи-

мых испытаниях интересующее нас событие появится к раз (много-

кратные повторные испытания), то применяют формулу Бернулли

(к) = С

, ' (1.14)

где р

(к) — искомая вероятность; С* — число сочетаний из п по к;

р — вероятность появления события в одном испытании, принимае-

мая одинаковой во всех опытах*.

Заметим, что ^ р

(к) есть вероятность того, что событие А появится

к=0

или 0, или 1 или п раз. Но указанное сложное событие есть полная

группа, поэтому ^ р

(к) = 1.

к=0

Приведем еще следующие полезные формулы:

1) вероятность того, что событие А появится не менее I раз, т. е.

к > /, определится так:

Рп(Ь>1)= %Рп(ЬУ, (1.15)

к=1

* В прил. I приведена таблица величии С^>'а в прил.^ХШ. 1 — программа

для калькулятора «Электроника БЗ-21» вычисления и р

(к).

а+Ь

а+6

с + а

2) вероятность того, что событие А появится не более I раз, т. е.

к < I, будет

Л, (*</)= 2 Л» (Л). (1-16)

*=о

При этом легко получить соотношение

{к^1) = 1+р

(1)-р

(к>1). (1.17)

Обозначим через А

событие, заключающееся в том, что интересую-

щее нас событие появится большее число раз, чем противоположное

событие, через Л

— меньшее число раз и через А

— одинаковое

число раз (при нечетном п р(А

) = 0) (например, событие — гер-

бов больше, Л

— гербов меньше, А

— одинаковое число появления

гербов и цифр при п бросании монеты).

Очевидно, имеет место зависимость

р(Л

) + р(Л

)+р(Л

) = 1, (1Л8)

причем, если р = У

, то /?(Л,) = р(А

1.116. По одной и той же мишени в одинаковых условиях производятся 4

независимых выстрела. Вероятность попадания в мишень при одном выстреле

р = 0,33 (? = 0,67). Определить вероятность поражения мишени к = 0, 1, 2, 3,

4 раза.

Решение. Так как р

(к) = С^р

п ~ 4 , то имеем:

/>4 (0) = С°р

д* = 1 • 0,33" • 0,67

= 0,20;

(1) = = 4 • 0,33' • 0,67з

о,40;

(2) = Су

> =

2 | |

• 0,33

• 0,67» = 0,29;

Р4 (3) = С

^ =

3 | [

• 0,33» • 0,67' = 0,10;

(4) = С>

<7° = 1 -О.ЗЗ'-0,67° =0,01.

Контроль: 2Рп(

) = 1,00.

В условии этой задачи вероятность попадания не менее двух раз

(к > 2) = р

(2) + р

(3) + р

(4) = 0,40;

не более двух раз

Р* (А < 2) = р

(0) + Р4 (1) 4- Р4 (2) =0,89

или по формуле (1.17)

(к< 2) = 1 + р

(2) -р

(6> 2) = 1 +0,29 -0,40 = 0,89.

Вероятность того, что попаданий больше, чем промахов, р[А

) = р

(3) +

/>1(4) = 0,11; одинаковое число промахов и попаданий р(Д

) =• р«(2) = 0,29.

Очевидно, что р(А

) = Р4(0) + Р4(1) = 0,60 — вероятность того, что попа-

даний меньше, чем промахов. Контроль по формуле (1.18): р(Л

) + р(А

) +

+ Р(А

) = 0,11 + 0,60 + 0,29 = 1,00.

1.117. Вероятность поражения цели равна 0,35. Для поражения цели не-

обходимо одно попадание. Определить вероятность поражения цели при 10 вы-

стрелах.

Ответ: 0,9865.

1.118. Вероятность поражения цели равна 0,8. Определить, какова вероят-

ность при 10 выстрелах поразить цель 5 раз; не менее 5 раз.

Ответ: 0,0191; 0,8339.

1.119. Произведено 10 измерений некоторой величины в одинаковых усло-

виях. Найти вероятность того, что 5 ошибок будет отрицательных и 5 — поло-

жительных; 3 ошибки — отрицательные и 7 — положительных.

1.120. По условиям задачи 1.119 найти вероятность того, что положитель-

ных ошибок будет не менее 5; более 7.

Ответ: 0,499; 0,097.

1.121. Найти вероятность того, что при 10 измерениях число появления от-

рицательных ошибок будет находиться в пределах от 0 до 5.

Ответ: 0,499.

1.122. Некоторая величина измеряется 3 раза. Определить вероятность того,

что положительная ошибка появится 3 раза; не менее, чем 2 раза.

Ответ: 0,125; 0,375.

1.123. Приняв вероятность рождения мальчика р = 0,515, найти вероят-

ность того, что среди 10 новорожденных будет 4 девочки.

Ответ: 0,217.

1.124. Имеется N лунок, по которым случайным образом разбрасывается М

шариков. Найти вероятность того, что в данную лунку попадет ровно к шариков.

к / \ \к [Ы—\ \м-к

Ответ: С., —

N / V N

1.125. Суд состоит из трех судей. Вероятность вынести справедливое реше-

ние каждым судьей одинакова и равна 0,7. Найти вероятность того, что: 1) суд

вынесет справедливое решение, 2) несправедливое решение. Сделать контроль

решения.

1.126. Два баскетболиста бросают мяч в корзину с вероятностью попада-

ния: первый — 0,7, второй — 0,6. Найти вероятности того, что: 1) первый из них

попадет больше раз, чем второй, 2) второй — больше, чем первый, 3) оба попадут

одинаковое число раз.

Указание. Для решения задачи составить следующие таблички:

1 II I II I II

10 0 1 0 0

2 0 0 2 1 1

2 1 12 2 2

в которых указаны варианты числа попаданий каждым баскетболистом, которые

соответствуют трем поставленным вопросам. Далее следует применить формулу

Бернулли для определения вероятности попадания р

' (к) и р

(к) и теоремы

сложения и умножения. Результаты решения задачи должны удовлетворять ус-

ловию Рх + р

+ р

= 1.

1.127. Прибор состоит из пяти узлов. Вероятность выхода за время I из

строя каждого узла одинакова и равна р = 0,10 + 0,0021, где < — номер фами-

лии студента по списку в журнале. Найти вероятность выхода из строя: 1) к =

0, 1, 2, 3, 4, 5 узлов, 2) хотя бы одного узла, не менее 4 узлов, 3) не более

4 узлов. Вычисление следует сопровождать контролями.

§ 7. ВЕРОЯТНЕЙШЕЕ ЧИСЛО ПОЯВЛЕНИЙ СОБЫТИЯ В СХЕМЕ

БЕРНУЛЛИ

Вероятнейшим числом появлений события при многократных ис-

пытаниях (к

) называется число, соответствующее наибольшей при

данных условиях вероятности. В обычном смысле — это наиболее

возможное число.

В математическом смысле число к

отвечает условиям:

Л, (*о) >/>»(*<>+1)5 Л,(*о)>Р»(Ао-1). (1-19)

В теории вероятностей доказывается, что условия будут соблюде-

ны, если

пр — с к

< пр + р\ (1.20)

отметим, что так как разность пр + р — (пр—<?) = р 4- <7 = 1, то

всегда существует целое число к

, удовлетворяющее написанному

выше двойному неравенству. При этом, если пр + р — число целое,

то вероятнейших чисел два: пр—<7 и пр + р.

В условии задачи 1.116 имеем:

4 . 0,33 — 0,67 < к

< 4 • 0,33 + 0,33,

или 0,65 < 1,65, откуда к

= 1.

Следует заметить, что левая и правая части неравенства (1.20) раз-

личаются на единицу.

1.128. Из многолетних наблюдений установлено, что вероятность выпадения

дождя 1 июля равна 0,227.Найти вероятнейшее число дней к

, когда в ближайшие

50 лет 1 июля выпадает дождь.

Решение. По условию задачи п = 50, р = 0,227,

пр — < к

< пр + р,

50 • 0,227 — 0,773 < < 50 • 0,227+0,227,

10,5< к

< 11,5.

Следовательно, за ближайшие 50 лет 1 июля наиболее возможное число

дождливых дней к

= 11.

1.129. Одна величина измеряется 20, а другая 25 раз. Определить вероятней-

шее число к

появлений положительной случайной ошибки в каждом случае.

Ответ: 10; 12 или 13.

1.130. Производится 7 испытаний. Вероятность положительного исхода в

каждом опыте равна — Подсчитать вероятнейшее число а положительных исхо-

дов и вероятность р* . '

О т в е т: а = 5; ра = 0,307.

1.131. Решить предыдущую задачу, если производится 8 испытаний.

Ответ: а = 5 или 6; р

= 0,273.

1.132. Сколько надо произвести независимых испытаний появления собы-

тия А, чтобы вероятнейшее число осуществления этого события было 450? Веро-

ятность р(А) при каждом испытании равна — .

Ответ: 675.

1.133. Предполагается сделать 400 независимых испытаний осуществления

события А. Как велика должна быть постоянная вероятность р(А) при каждом

испытании, чтобы вероятнейшее число появления события А было равно 150?

Ответ: 0,375.

1.134. Сколько раз надо подбросить игральную кость, чтобы вероятнейшее

число выпадений двойки было равно 32?

Р е ш е н и е. В данном случае р = —, т

= 32. Требуется найти число не-

зависимых испытаний п. Величины р, = 1 — р, ш

и п связаны между собой

неравенством пр — ц ^ т

< пр + р, откуда

15 11

л—— —<32; л —+—>32.

6 6 6 6

Из первого неравенства я 197, а из второго —я 191. Таким образом,

необходимо провести от 191 до 197 независимых испытаний.

1.135. Вероятность изготовления нестандартной детали р= 0,05. Сколько

деталей должно быть в партии, чтобы вероятнейшее число нестандартных дета-

лей в ней было равно 63?

Ответ: 1259 < л < 1279.

1.136. Каждая нз 6 палочек разламывается на две части — длинную и ко-

роткую. Затем 12 полученных обломков я раз объединяются в 6 пар, каждая из

которых образует новую палку. Чему равно л, если вероятнейшее число объеди-

нений обломков в первоначальном порядке равно 6.

Ответ: 1/1111, 62 369 < л < 72 764.

§ 8. ЛОКАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА

Пользоваться формулой Еернулли при больших значениях трудно,

так как формула (1.14) требует выполнения действий над громадными

числами. Локальная теорема Лапласа дает асимптотическую формулу,

которая позволяет приближенно найти вероятность появления собы-

тия ровно к раз в п испытаниях, если число испытаний достаточно ве-

лико.

Локальная теорема Лапласа. Если вероятность р появления собы-

тия А в каждом испытании постоянна и отлична от нуля и единицы, то

вероятность Р

(к) того, что событие А появится в п испытаниях ровно

к раз, приближенно равна (тем точнее, чем больше п) значению функ-

ции

Упрд У 2л У^прд

где х = к—пр/упрс].

Имеются таблицы, в которых помещены значения функции у =

= ф(дг) = е 2, соответствующие положительным значениям

аргумента х (прил. II). Для отрицательных значений аргумента поль-

зуются теми же таблицами, так как функция ср(х) четна, т. е. ф(—х) =

= ф(*).

Итак, вероятность того, что событие А появится в п независимых

испытаниях ровно к раз, приближенно равна

(1.21)

РЧ

х = (к — пр)1\Пхрц.

(1.22)

1.137. Найти вероятность того, что событие А наступит ровно 80 раз в 400

испытаниях, если вероятность появления этого события в каждом испытании

равна 0,2.

Решение. По условию л = 400; к = 80; р = 0,2; 9 = 0,8.

Воспользуемся асимптотической формулой Лапласа

(80)« ' — ?(*) = 4" ? (*)•

у 400

•

0,2 • 0,8 °

к — пр 80 — 400 0,2

Вычислим х = = г = 0.

У лр<? °

По таблице (прил. II) находим ф(0) = 0,3989. Искомая вероятность Р

400

(80)^;

» 1/8 • 0,3989 = 0,04986.

По формуле Бернулли Р

4ОО

(80) = 0,0498*.

1.138. Вероятность изготовления детали высшего сорта на данном станке

равна 0,4. Найти вероятность того, что среди наудачу взятых 26 деталей половина

окажется высшего сорта.

Ответ: 0,093.

1.139. Выполнено 40 измерений. Найти вероятность того, что положитель-

ная ошибка появится в 25 случаях.

Ответ: 0,036.

1.140. Бюффон бросил монету 4040 раз. При этом герб выпал 2048 раз. С

какой вероятностью можно было ожидать этот результат?

Ответ: 0,0085.

1.141. Найти вероятность выпадения герба 4 раза при 10 бросаниях монеты.

Решение. Имеем

/ = (4 — 5)//2Т5 = 0,632, у' =0,460,

Ы =

//275=0,632.

На основании формулы (1.21)

^ю (

)= —=0,460 - 0,632 = 0,207.

Биноминальное распределение дает Яю(4) = 0,205.

1.142. Приняв вероятность рождения мальчика равной 0,515, найти вероят-

ность того, что среди 80 новорожденных 42 мальчика.

Ответ: 0,009.

1.143. Стрелок сделал 30 выстрелов с вероятностью попадания при отдель-

ном выстреле 0,3. Найти вероятность того, что при этом будет 8 попаданий.

Ответ: 0,147.

1.144. Английский ученый Пирсон, подбросив монету 12 000 раз, получил

частость выпадения герба 0,5016. Найти вероятность получения такой частости

при повторном опыте.

Ответ: 0,007.

1.145. Сколько раз с вероятностью 0,0484 можно ожидать появления собы-

тия А в 100 независимых испытаниях, если вероятность его появления в отдель-

ном испытании равна 0,5?

Ответ: 55.

§ 9. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ФОРМЫ ЗАДАНИЯ ЗАКОНА

РАСПРЕДЕЛЕНИЯ. ФУНКЦИЯ И ТОЧНОСТЬ РАСПРЕДЕЛЕНИЯ.

ВЕРОЯТНОСТЬ ПОПАДАНИЯ В ИНТЕРВАЛ

Одним из важнейших основных понятий теории вероятностей яв-

ляется понятие о случайной величине.

Случайной называется величина, которая в результате опыта мо-

жет принять то или иное одно значение, причем неизвестно заранее,

какое именно. Примером случайных величин являются: 1) число по-

* Вычислено с помощью логарифмических таблиц, приведенных в «Табли-

цах математической статистики» (Большее А. Н., Смирнов Н. В. М., Наука,

паданий при п выстрелах, 2) результат измерения какой-либо вели-

чины, 3) координаты точек попадания при стрельбе и т. д.

Случайные величины могут быть прерывными (дискретными) и не-

прерывными.

Прерывной случайной величиной называют такую случай-

ную величину, возможные значения которой можно заранее указать

(вышеприведенный пример 1).

Непрерывной случайной величиной называют случайную

величину, возможные значения которой непрерывно заполняют не-

который промежуток и не могут быть перечислены заранее (примеры

2 и 3).

От событий, понятием которых мы оперировали в главе 1, всегда

можно перейти к случайным величинам. Пусть производится опыт,

в котором может появиться или не появиться событие А.

Вместо события А можно рассматривать случайную величину X,

равную 1, если событие А происходит, и равную 0, если событие А

не происходит.

В отличие от величины неслучайной случайную величину недоста-

точно характеризовать числом, необходимо каждому из ее возможных

числовых значений приписывать вероятность появления этих значе-

ний.

Всякое соотношение, устанавливающее связь между возможным

значением случайной величины и соответствующими вероятностями,

называют законом распределения случайной величины. Закон распре-

деления — фундаментальное понятие теории вероятностей.

Для характеристики закона распределения прерывной случайной

величины часто применяются ряд (таблица) и многоугольник распре-

деления. Если X — случайная величина, которая может принять зна-

чения Х

, ..., Х

, то ряд распределения имеет вид

•X; I Х

•

Р1 I

Р\Р%

••• Рп

(1.23)

в которой перечислены возможные значения случайной величины X и

соответствующие им вероятности. Так как в таблице перечислены все

возможные значения Х

,то V/?,. = 1. Например, для случайной вели-

1=1

чины к — числа появлений положительной ошибки при 8 измерениях

ряд распределения имеет следующий вид:

Число появ- 0 1 2 3 4 5 6 7 8

Конт

лении к роль

5 6

70 55

8 1

256 256

256 255

256

1 8 28 56 70 55 28 8 _1_ 256

Р1

256 256 256 256 256 255 256 255 256 256

Здесь вероятности р

вычислены по формуле (1.14) Р

(к) —

= С1р*с/

(р =

). Чтобы придать ряду распределения более на-

глядный вид, прибегают к его графическому изображению, отклады-

вая по оси абсцисс значения X а по оси ординат — вероятности. Кон-

РИС. 3

РИС. 4

о 1 г 3 Ь 5 6 7 в н

О X х

цы ординат соединяют ломаной линией. Полученная фигура называет-

ся многоугольником распределения. Так, для приведенного выше

ряда распределения многоугольник имеет вид, представленный на

рис. 3.

Для задания закона распределения как прерывной, так и непре-

рывной случайной величины служит так называемая функция рас-

пределения. Функцией распределения называется вероятность того,

что случайная величина принимает значение, меньшее некоторого за-

данного значения х случайной величины X, т. е.

Функцию Р(х) называют еще интегральной функцией распределе-

ния. Приведем ее некоторые свойства:

I) Р{— оо) = 0; 2) /

(+оо) = I; 3) Р(х

) > Р(хД, если х&х^

Эти свойства легко иллюстрировать с помощью геометрической ин-

терпретации как вероятность попадания на отрезок левее точки х,

расположенной на числовой оси х (рис. 4).

1.146. Построить функцию распределения для случайной величины Х= к

числа попаданий в мишень при четырех выстрелах, если вероятность попадания

при одном выстреле р = 0,33.

Решение. Ряд распределения (см. задачу 1.116) имеет вид

1>1 0 12 3 4

Р1 = Р4 ( к( ) 0,2Л 0,40 0,29 0,10 0,01

Из определения функции Р(Х) (1.24) и ряда распределения следует:

1) при *<0 Р (к = 0) = р (к < 0) = 0;

2) » к= 1 Р(к= 1) =р(к< 1) =р (к = 0) =0,20;

3) » к = 2 Р (к =2) =р(к < 2) =р(к =0) (*=

= 0,60.

Аналогично рассуждая, имеем:

4) при к = 3 Р (к = 3) = 0,89;

б) » к = 4 Р(к= 4) = 0,99;

6) » к > 4 Р (к > 4) = 1,00.

/г— 1

Общая формула Р (к) = ^ Рп (*)•

4=0

Функция распределения

Р(х) = Р(Х<х).

(1.24)

Г(к)

а,75

0,50

025

^ ь

О / 2 3 4 к

х с(х

Откладывая по оси абсцисс значение к, а по оси ординат Р(к) и

выбрав определенный масштаб, получим график Р(к) (рис. 5).

Закон распределения для непрерывной случайной величины удоб-

но задавать в виде плотности распределения (кривой распределения),

которая определяется как производная от функции распределения,

т. е.

1>ш

рг

{х) = ф (х

\х

(1.25)

Плотность ф(лг) называется еще дифференциальным законом рас-

пределения (а функция Р(х) — интегральным законом).

Плотность ф(х) обладает свойствами:

1) ф(Л:) > 0; 2) | СР(л:)0х= 1,

(1.26)

т. е. площадь, заключенная «под кривои распределения», всегда рав-

на 1. Если все возможные значения X заключены в пределах от а до |5,

то

^ ф (х) йх = 1.

(1.27)

Величину у(х)йх, выражающую с точностью до бесконечно малой

вероятность попадания на участок йх, примыкающий к точке X, на-

зывают элементом вероятности (рис. 6).

Очевидно, что Р(х) и ф(х) связаны соотношением

Р(х)= \ ф (х)<1х.

(1.28)

Вероятность попадания на участок выражается через плотность

так:

Я{«<Х<р} = (1.29)

1.147. Случайная величина X подчинена закону распределения с плотностью

•к я

? (*) = а соз * при — — < х < — ;

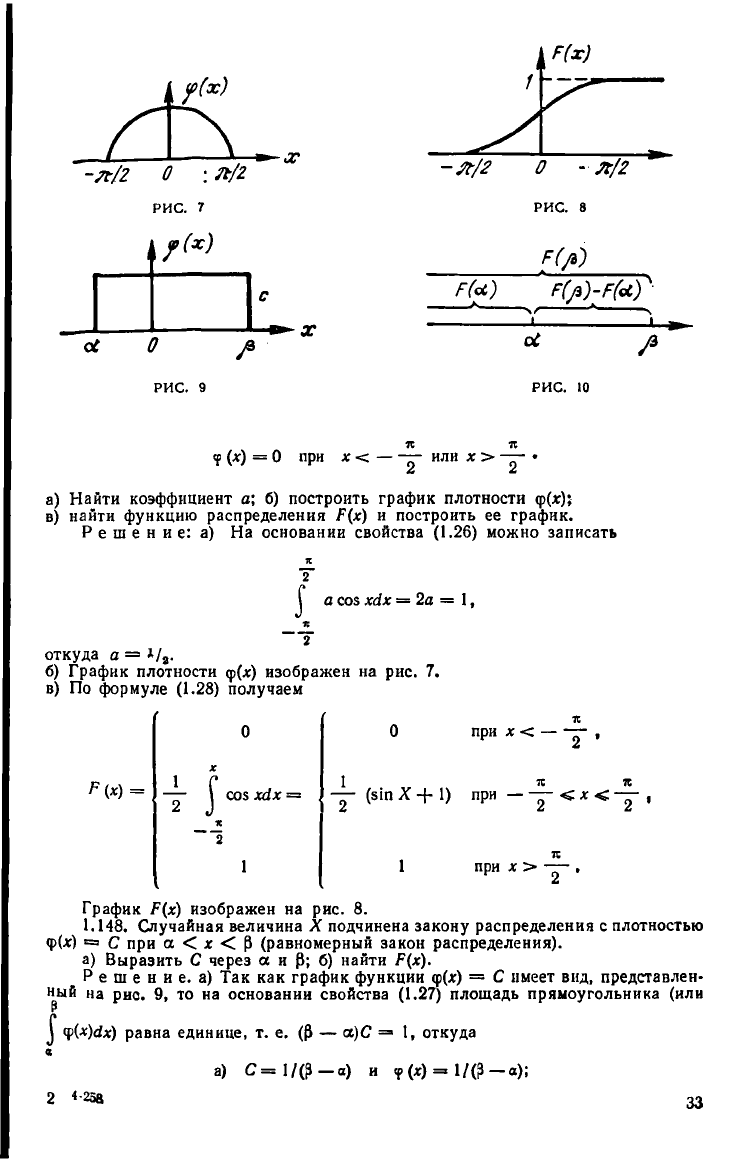
-л/2 0 : Л/2

РИС. 7

>г

(х)

ос О р

РИС. 9

/м

-Л/2

7 - Л/2 *

РИС. 8

Г(л)

_1_

РИС. 10

К 1С

<р

(х) = 0 при х < — — или X > — •

а) Найти коэффициент а; б) построить график плотности <р(*);

в) найти функцию распределения Р(х) и построить ее график.

Р е ш е н и е: а) На основании свойства (1.26) можно записать

а соз хЛх = 2а = I,

откуда а = */

б) График плотности <р(*) изображен на рис. 7.

в) По формуле (1.28) получаем

Г(х) =

-И

соз хЛх =

при

<. —

2 '

-у

(5111

X + 1) при

1 при

> .

График Р(х) изображен на рис. 8.

1.148. Случайная величина X подчинена закону распределения с плотностью

ф(*) =» С при а < * < р (равномерный закон распределения),

а) Выразить С через а и Р; б) найти Р(х).

Р е ш е н и е. а) Так как график функции <р(*) = С имеет вид, представлен-

ный на рио. 9, то на основании свойства (1.27) площадь прямоугольника (или

4>{х)(1х)

равна единице, т. е. ((} — а)С = 1, откуда

а) С =

/ (Э — а) и ?(*) = 1/(Э-а);

2 4258