Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

(2.121)

а для независимых аргументов в виде

1 VI ( д! у 1

2.93. Используя условия задачи 1.225, найти вес функции

и = 2х + У-

Решение. На основании формулы (2.121) имеем

Ри Рх Ру УРхРу

При этом г = +0,5, о

—

- Приняв за с. к. о. единицы веса о

с. к. о. а

измерения аргумента г, получаем р

= а

/о^2 = 1/2 = р

. Поэтому

1/р

= 4/2+1/2+ 4. 0,5/2 = 3.

В следующих задачах будем рассматривать лишь независимые измерения.

2.94. Найти веса следующих функций:

1) и = х — у + г, 3) и = Зх

2) ц=2х + -^ I^ г,

если р

= 3, р

= 1/3 и р

= 1/4.

Решение.

11111 ,1 3

1) — = — + — + — =^" + 3 + 4 = 7 —; Р

= —:

Ри Рх Ру Рг 3 3 22

1 1118 3

2) = 4- — + — . 3 + — • 4 = — ; Р

= — I

р„ 3 9 4 3 8

ч 1 1 36х

2.95. Найти вес площади треугольника, если основание его 6 = 8 получено

с весом рь = 1. высота Л = 16 с весом рд = Ь2.

Решение. Составляем функцию измеренных величин 5=1/2' ЬН,

затем находим

1 I дЗ 1 / 35 1 ( 1 V I 1 \

——= (-—-) —+ [— — = —Л -1+ —

-2 = 64 + 32 = 96.

Рз \ дЬ ) р

\ дН ) рь \2 ) ^Л 2 )

2.96. Найти вес функции

1Р1

1=1

и = ^ >

1=\

где Х[ — результаты измерения, а р

— их веса.

Решение. Имеем ^ " = . Поэтому

дх

{

Ър1

124

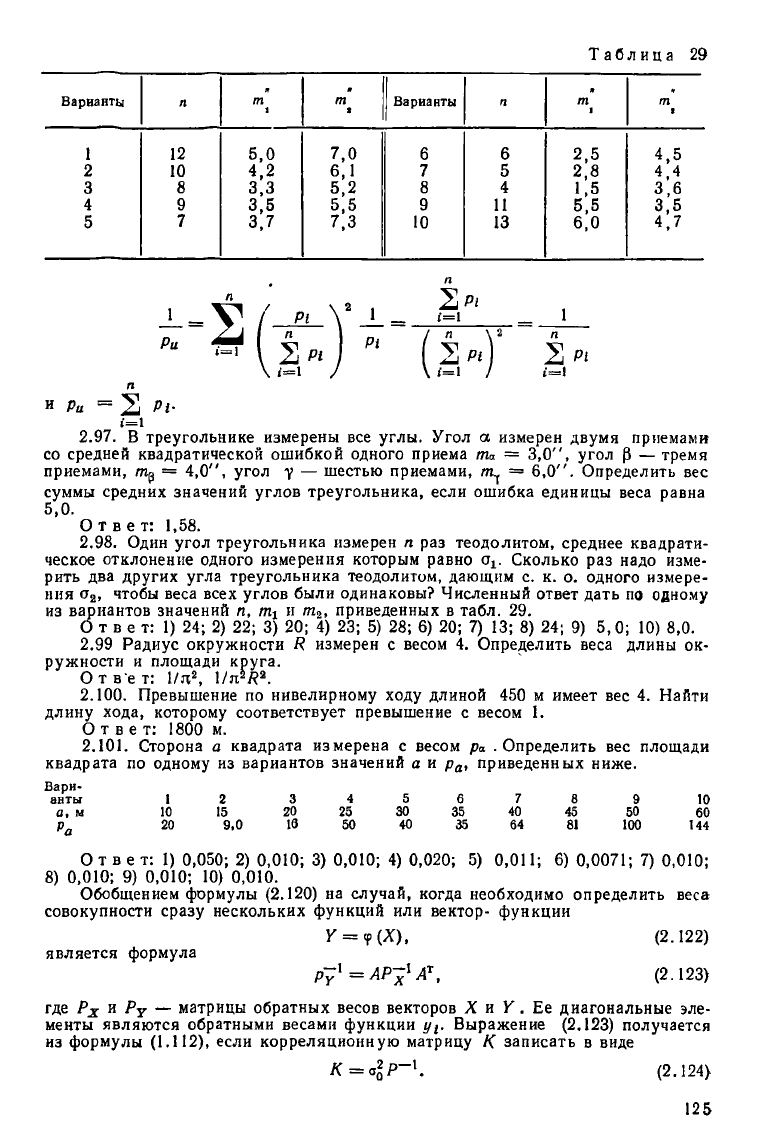
Таблица 29

Варианты

5,0

4.2

3.3

3,5

3,7

7.0

6.1

5.2

5,5

7.3

2,5

2,8

1,5

5,5

6,0

1 _ 1 _ (=1

Ра

2 Л 2 Р1

1=\ / 1=1

и Ри =2 Р1-

{=1

2.97. В треугольнике измерены все углы. Угол а измерен двумя приемами

со средней квадратической ошибкой одного приема та = 3,0", угол Р — тремя

приемами, т^ = 4,0", угол у — шестью приемами, т^ = 6,0". Определить вес

суммы средних значений углов треугольника, если ошибка единицы веса равна

5,0.

Ответ: 1,58.

2.98. Один угол треугольника измерен п раз теодолитом, среднее квадрати-

ческое отклонение одного измерения которым равно Сколько раз надо изме-

рить два других угла треугольника теодолитом, дающим с. к. о. одного измере-

ния сг

, чтобы веса всех углов были одинаковы? Численный ответ дать по одному

из вариантов значений п, т

и т

, приведенных в табл. 29.

Ответ: 1) 24; 2) 22; 3) 20; 4) 23; 5) 28; 6) 20; 7) 13; 8) 24; 9) 5, 0; 10) 8,0.

2.99 Радиус окружности К измерен с весом 4. Определить веса длины ок-

ружности и площади круга.

Ответ: 1/л

, 1/я

2.100. Превышение по нивелирному ходу длиной 450 м имеет вес 4. Найти

длину хода, которому соответствует превышение с весом 1.

Ответ: 1800 м.

2.101. Сторона а КВЙДрЗТЯ

ИЗ

МСрСНЗ С 66С0М ра . Определить вес площади

квадрата по одному из вариантов значений а и р

, приведенных ниже.

Вари-

анты 12 345678 9 10

о, м 10 15 20 25 30 35 40 45 50 60

20 9,0 16 50 40 35 64 81 100 1 44

Ответ: 1) 0,050; 2) 0,010; 3) 0,010; 4) 0,020; 5) 0,011; 6) 0,0071; 7) 0,010;

8) 0,010; 9) 0,010; 10) 0,010.

Обобщением формулы (2.120) на случай, когда необходимо определить веса

совокупности сразу нескольких функций или вектор- функции

К = =р(Х), (2.122)

является формула

р-

=АРх

, (2.123)

где Р

и Я

— матрицы обратных весов векторов X и V. Ее диагональные эле-

менты являются обратными весами функции Выражение (2.123) получается

из формулы (1.112), если корреляционную матрицу К записать в виде

К = о§р-

. (2.124)

125

Напомним, что матрица

определяется согласно (1.113).

2.102. Известно, что матрица обратных весов уравненных углов (исправ-

ленных поправками после распределения угловой невязки) полигонометричес-

кого хода имеет вид [3]

(2.126)

где я + 1 — число углов хода. Найти матрицу обратных весов первого и второго

дирекционных углов сторон, если п = 6.

Решение. Составляем функции, связывающие углы с дирекционными

углами. Имеем

Матрицы

П оэтому

1 \ / «нач \

I «нач + + М '

/1 0 0 0 0 0\

~\1 1 ООО 0/ *

6 —1 —1 —1 —1 —1

—1 6—1—1—1—1

= 1 —1 6 —1 —1 —1

-I _ /1 0 0 0 0 0\ _1_

и 1 О О О о) 7

к—1 —1 —1 —1 —1 6

Отсюда следует, в частности, что

/р

= 6/7; 1 /р

= 10/7; р

= 7/6; р

=»

= 7/10.

Коэффициент корреляции г

= ———= 0,645.

" " У 6 /10

2.103. Составить матрицу обратных весов функций Д* <= 5соза, Ду =>

= 5зша, если даны веса р

и р

2.104. Даны функции у

= х

— х

= х

— х

и матрица обратных ве-

сов вектора х

• /0,5-1 —0,5\

Р = -1 1 -0,2 .

\—0.5 -0,2 2 )

Найти матрицу Р~

и матрицу Р

Ответ:

1 =

/ 3,5 -1,7\ /0,377 0,189\

у \—1,7 3,4/'

\0,189 0,388/'

126

§ 25. ОБРАБОТКА РЯДА НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ ОДНОЙ

ВЕЛИЧИНЫ

В § 20 рассмотрено, как решается задача обработки ряда равно-

точных измерений одной и той же величины. Пусть теперь имеем ряд

независимых измерений (х

, ..., х

) с весами, соответственно рав-

ными ри р

, ..., рп- В этом случае наилучшей оценкой для математи-

ческого ожидания М

, а в случае отсутствия систематических

ошибок — для X будет так называемая общая арифметическая сре-

дина (весовая средняя)

х=1рх]/[р], (2.127)

а для дисперсии единицы веса — квадрат средней квадратической

ошибки

= И

]/(я — 1) (2.128)

(формула_Бесселя для неравноточных измерений), где, как и ранее,

V= XI — х. Отклонения от общей арифметической средины облада-

ют свойствами [ро] = 0, [/?и

] = гшп.

Величина х определяется с точностью

т. = М = ц 1У\р], (2.129)

а в случае наличия систематических ошибок

м=

(2Л30)

Имеют место формулы -

т^яц1/У2(п — 1), т

ыщ1У\Р\- (2.131)

Доверительные интервалы для истинного значения X и дисперсии

единицы веса строятся аналогично тому, как это делается при обра-

ботке равноточных измерений, и имеют вид

(2.132)

х — („т. < X < х + 1

т- ;

р X Р X

УУ < оЦ Т

Н.

Для ст

и а? имеем доверительные интервалы

(2.133)

Ът- < а- < у

т-. (2.134)

Заметим, что если известны истинные ошибки измерений Л, =

= X/ — X, то задача сводится только к оценке точности измерений

по формуле Гаусса

ц« = [рД»]/л. (2.135)

127

Вычисления при обработке ряда неравноточных измерений выпол-

няются в следующем порядке.

1. Вместо (2.127) удобно применять формулу

Г= х' + [ер]/[р],

где е

(

= XI—х', х'= гшги

(

2. Вычисляют уклонения у, и выполняют контроль = —р[р],

где ошибка округления при вычислении х будет р = ДГ

ОК

Р—*

очн-

3. Вычисляют [ру

] с контролем

[ръ*\ = [*»•] - [ре]

/*,

ошибки [л, М, т^ тм или строят доверительные интервалы.

Результат записывают в виде х

± М или в виде доверительного

интервала.

Заметим, что оба значения [х [принятое для вычисления весов и

полученное по формуле (2.128)1 должны совпадать в пределах ошибки

Их расхождение на величину, большую чем т^ указывает на

наличие систематических ошибок.

2.105. Произвести математическую обработку по данным, приведенным в

табл. 30, в которой даны средние значения одного и того же угла, измеренного

разным числом приемов п. Для удобства вычислений целесообразно применять

формулу Р1 = п/3. Вычисления располагаем в этой же таблице.

Таблица 30

Число

прие-

ыэв п

р=

~г

р«

ро-

89° 47' 16"

+10

+20 200

+ 12

18 6

+18 54

— 1

—6 6

6 3

1 0

—4

+20

23 6 2

+14

+3 +6 18

8 12 4

+2 + 8

—2 —8

*'=89

4 Г 06"

|Р

,Т" = +

.°

2=20

2= +80 2=448

—18

+18

2=0

2=128

=8947'10,0"

Р=0

/2(Г * г/ 2(п—11

5,1

/1о

/20"

= 1,6";

•

/|р|

-=0,36".

12.

Таблица 31

Номера

линия

196.529

196,522

196,517

196,532

196.530

196,520

6.3

8.4

9.1

4,3

5.2

7.5

0,25

0,14

0,12

0,54

0,37

0,18

+ 12

+ 15

+ 13

3,00

0,70

8,10

4,81

0,51

Р»

36,0

3.5

121,5

62,5

1.6

+1.3

-5,7

—10,7

+4,3

+2,3

—7.7

+0,33

-0,80

1,28

+2,32

+0,85

—1,39

0,4

4,6

13,7

10,0

2,0

10,7

= 196,517

[ р ] = 1,60 I = 17,15

[рг

]=225,1

—3,47 41,4

+3,50

[Р*1

[Р]

= +Ю,7

*= 196,5277

1И

[р]

[/»] =+0,03

+ 17,15

=+10,72 мм =0,01072

1,60

= — 0,02; — [р] Р = 0,03;

294,1

м;

[ре

] = 2251

1.6

= 41,3.

Ответ: 89°47'10,0"± 1,1".

Доверительные интервалы при Р = 0,95 имеют вид

89'47'06,9" < X < 89'47'13 ,1"

(коэффициент /р = 2,8 выбираем из таблиц распределения Стьюдента по Р =

= 0,95 и числу степеней свободы г = 6—1 = 5). Для построения доверительно-

го интервала для по таблицам распределения к

по числу степеней свободы

г = п — 1 и вероятности Р = 0,95 находим у! = 0,624, у

2,45. Тогда

3,18" с

Сд

с 12,45".

Далее получаем доверительные интервалы 1,8" ^ а

^ 3,5" и 0,40" <

< а- < 0,78".

2.106. Отметка Я точки местности получена по шести нивелирным линиям.

Произвести полную математическую обработку результатов измерений по дан-

ным, приведенным в табл. 31.

Средняя квадратическая ошибка единицы веса

41,4 2,9

г = 2,9 мм, а т =

= 0,92 мм.

6—1 ^ /2(6—1)

/Г = УТй = 3,1. Поэтому

М = 2,9/^1,6 =2,3 мм, т

Л1

= 0,92/^1,6 =0,73 мм.

4 258

129

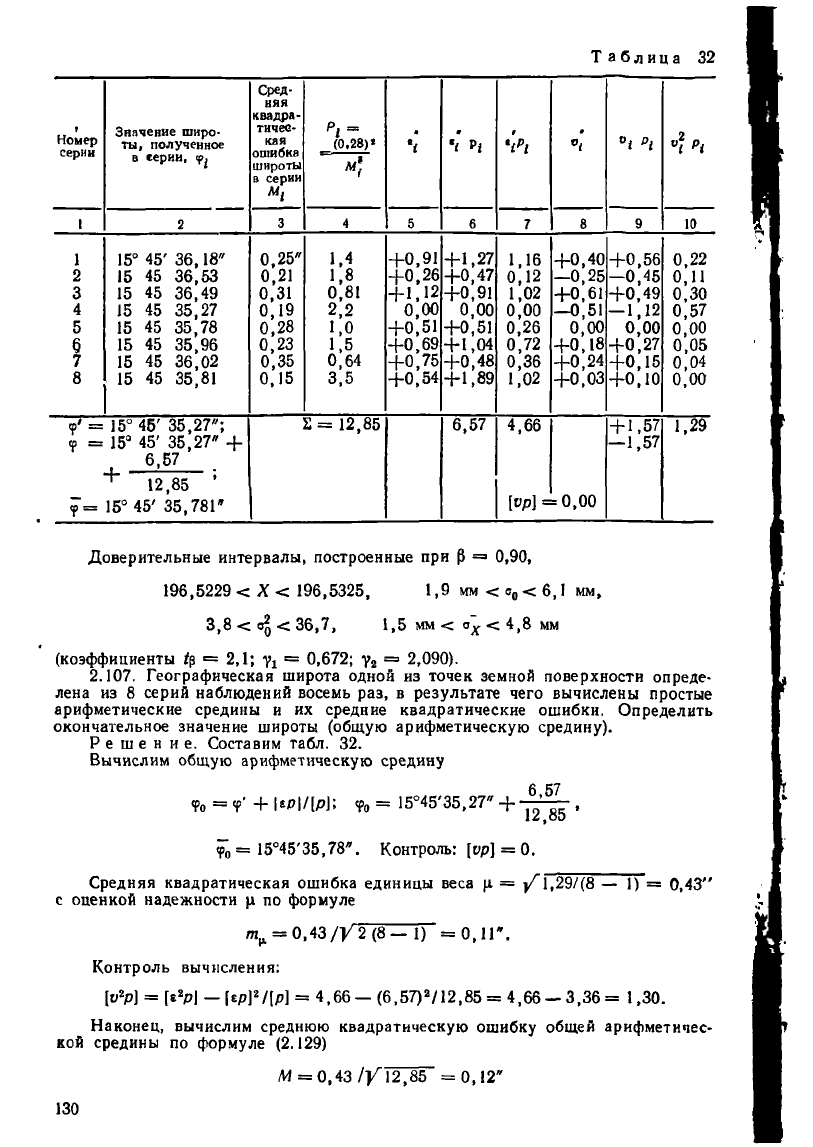
Таблица 54'

Значение широ-

ты, полученное

в серии, ф.

Сред-

няя

квадра-

тичес-

кая

ошибка

широты

в серии

(0.28)«

М,

"I "1

15°

45'

3 15

36,53

36,49

35,27

35,78

35,96

36,02

35,81

0,25"

0,21

0,31

0,19

0,28

0,23

0,35

0,15

1.4

1.8

0,81

2,2

1,0

1.5

0,64

3,5

+0,91

+0,26

+1,12

0,00

+0,51

+0,69

+0,75

+0,54

+1,27

+0,47

+0,91

0,00

+0,51

+1,04

+0,48

+1,89

1,16

0,12

1,02

0,00

0,26

0,72

0,36

1,02

+0,40

—0,25

+0,61

—0,51

0,00

+0,18

+0,24

+0,03

+0,56

—0,45

+0,49

-1,12

0,00

+0,27

+0,15

+0,10

= 15° 45' 35,27";

ф = 15° 45' 35,27" +

6,57

12,85

<р= 15° 45' 35,781"

2 = 12.85

6,57

4,66

[ор] = 0,00

+ 1,57

-1,57

Доверительные интервалы, построенные при ($ =• 0,90,

196,5229 < Х< 196,5325, 1,9 мм<о

<6,1 мм,

3,8 <

Од

< 36,7, 1,5 мм < О^ < 4,8 мм

(коэффициенты /р = 2,1; у

= 0,672; у

= 2,090).

2.107. Географическая широта одной из точек земной поверхности опреде-

лена из 8 серий наблюдений восемь раз, в результате чего вычислены простые

арифметические средины и их средние квадратические ошибки. Определить

окончательное значение широты (общую арифметическую средину).

Решение. Составим табл. 32.

Вычислим общую арифметическую средину

Ъ = <Р

+ \*Р\№\ 9о = 15°45'35,27" ,

% = 15°45'35,78". Контроль: [яр] = 0.

Средняя квадратическая ошибка единицы веса ц = /1,29/(8 — 1) = 0,43"

с оценкой надежности р по формуле

т^ = 0,43 /У 2 (8 - 1) = 0,11".

Контроль вычисления:

[IРр\ = [е

р| — [ер]

/[р] = 4,66- (6,57)

/12,85 = 4,66 —3,36 = 1,30.

Наконец, вычислим среднюю квадратическую ошибку общей арифметичес-

кой средины по формуле (2.129)

Л4 = 0,43//12,85 =0,12"

130

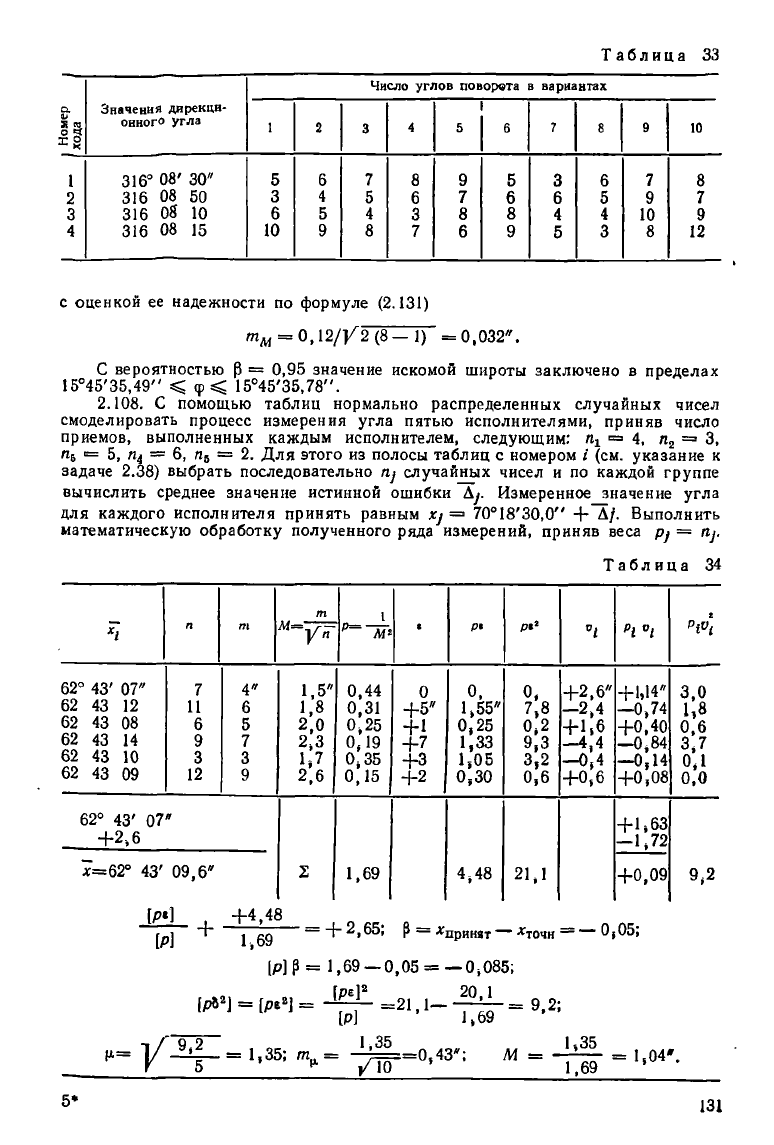
Таблица 128

г>

= 8

Значения дирекцв-

онного угла

Число углов поворота вариантах

г>

= 8

Значения дирекцв-

онного угла

1 316° 08' 30"

5 6

8 9

316 08 50

6 6 5 9

3 316 08 10

6 5 4

316 08 15

10 9 8

6 9

3 8 12

с оценкой ее надежности по формуле (2.131)

= 0,12/^2 (8— 1) = 0,032".

С вероятностью Р = 0,95 значение искомой широты заключено в пределах

15°45'35,49" ^ ф< 15°45'35,78".

2.108. С помощью таблиц нормально распределенных случайных чисел

смоделировать процесс измерения угла пятью исполнителями, приняв число

приемов, выполненных каждым исполнителем, следующим: =4, п

= 3,

= 5, щ — 6, п

= 2. Для этого из полосы таблиц с номером I (см. указание к

задаче 2.38) выбрать последовательно Лу случайных чисел и по каждой группе

вычислить среднее значение истинной ошибки Ду. Измеренное значение угла

для каждого исполнителя принять равным X] = 70°18'30,0" + Д/. Выполнить

математическую обработку полученного ряда измерений, приняв веса р^ = Пу.

Таблица 34

62°

43' 07"

43 12

62 43 08

6 5

43 14

9 7

43 10

3 3

43 09 12

-уп

1,5"

1,8

2,0

2,3

2.6

0,44

0,31

0,25

0,19

0,35

0.15

62° 43' 07"

+2,6

*=62° 43' 09,6"

[р«1

1,69

+5"

1,55'

0,25

1,33

1,05

4,48

0,2

9,3

3,2

0,6

21.1

+2,6"

-2,4

+1,6

-4,4

—0,4

+0,6

О.

+1,14"

—0,74

+0,40

—0,84

—0,14

+0,08

+1 >63

—1,72

+0,09

ЬР1

+4,48 _ _ _

"г 1 59 65; р = ^принят — *точн

— 0,05;

[р]Р = 1,69 — 0,05 = — 0,085;

[ра*] = [ре°]=-^ -21.1-4^— 9,2;

<*= у'-

9,2

•

= 1,35; =

[р] ' 1,69

^--0 43"

М =

1,35

1,69

= 1,04'.

131

Таблица 54'

Номера

Не-

Варианты

Номера

Не-

поли-

вязки ,

7 8 9 10

гонов

мм

Число

станций

—7.5

49 52 57

-8,5 56 51

3 +3,9 72

105

+5,7

98 90

103 107 114

125 133

142

5 — 14,1

167

152

174

181

193

211 226

241

130 145

—5,0

105

+8,2

113 103

118

123

131 144

151

164

+3,7

94 98

104

114 122

130 70 78

—4,6

117

106

122

127

135

148

158

169

91 101

10 +6,4 53 46

54 53

68 72 39

+9,7

68 72

85 90

49 54

2.109. Сделать то же самое, введя в каждый угол дсу систематическую ошиб-

ку с = 1". Проверить неравенство |а

— |д| < щ , где а принята равной 1".

2.110. Выполнить обработку всех я = 2

20 равноточных измерений

/=»

угла по данным задачи 2.108 и сравнить результаты с полученными в этой зада-

че.

2.111. Дирекционный угол стороны полигонометрического хода получен из

4 ходов, сходящихся в одной узловой точке. Ходы имеют разное число углов по-

ворота.

Вычислить наилучшее значение дирекционного угла и найти его среднюю

квадратическую ошибку, а также среднюю квадратическую ошибку измерения

отдельного угла полигонометрического хода. Результаты наблюдений даны в

табл. 33 [1].

2.112. Угол измерен разными теодолитами и различным числом приемов.

В табл. 34 даны средние арифметические числа приемов я,, средние квад-

ратические ошибки результата измерения из одного приема т

. По этим дан-

ным определить х и произвести оценку точности полученных результатов.

Ответ: 62°43'09,6"± 1,04".

2.113. Произвести оценку точности нивелирных работ по невязкам, приве-

денным в табл. 35, в 11 полигонах [7]. Найти средние квадратические ошибки

превышений на одной станции и на 1 км хода.

2.114. При исследовании трех новых теодолитов был многократно измерен

один и тот же угол. В табл. 36 приведены результаты измерений. Определить:

1) какой теодолит дает лучший результат при однократном измерении угла,

для чего вычислить х, т и т

по результатам измерений каждым теодолитом;

2) окончательное значение угла как результат измерения всеми тремя теодо-

литами и его среднюю квадратическую ошибку.

§ 26. ОЦЕНКА ТОЧНОСТИ ПО РАЗНОСТЯМ ДВОЙНЫХ НЕРАВНОТОЧНЫХ

ИЗМЕРЕНИЙ

Если разности двойных измерений — х

(

—х

(

(I = 1, 2, ..., п)

получены по неравноточным измерениям х

{

, но попарно равноточным,

т. е. (р

Х[

= р

'), то имеем обратный вес разности

132

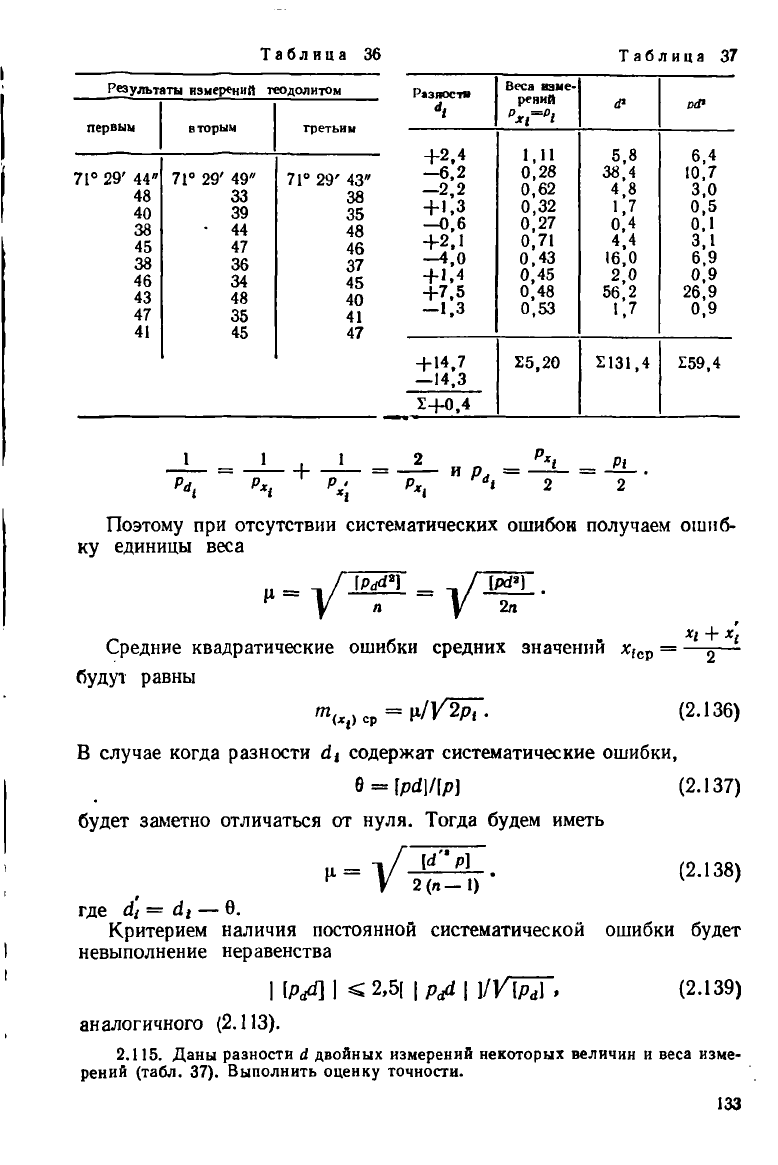
Таблица 36

Таблица 37

Результаты измерений теодолитом

первым

вторым

третьим

71° 29' 44"

71° 29' 49"

71°29' 43"

48 33

• 44

45 47

36 37

43 48

35 41

45 47

Развоет»

+2.4

-6.2

-2,2

+1.3

—0,6

+2.1

-4.0

+1.4

+7.5

—1.3

+ 14.7

-14,3

2+0,4

Веса наме-

рений

"хГ

< "I

1,11

0,28

0,62

0,32

0,27

0.71

0,43

0,45

0,48

0,53

25.20

<Р

5,8

38,4

4,8

1,7

0,4

4,4

16,0

2,0

56,2

1.7

2131,4

_1 1

Рх

(

х\ ~ % " 2 2

Поэтому при отсутствии систематических ошибон получаем ошиб-

ку единицы веса

свадра-

будут равны

[Р4Ч

2п

XI + х'.

Средние квадрэтические ошибки средних значений лг

гср

= —^—

(х

ср = р/УЖ- (2.136)

В случае когда разности содержат систематические ошибки,

6 = И1/[Р] (2.137)

будет заметно отличаться от нуля. Тогда будем иметь

где (1{ = — 6.

Критерием наличия постоянной систематической ошибки будет

невыполнение неравенства

1МК

( I р^ I МУШ> (2.139)

аналогичного (2.113).

2.115. Даны разности Л двойных измерений некоторых величин и веса изме-

рений (табл. 37). Выполнить оценку точности.

133.