Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений
Подождите немного. Документ загружается.

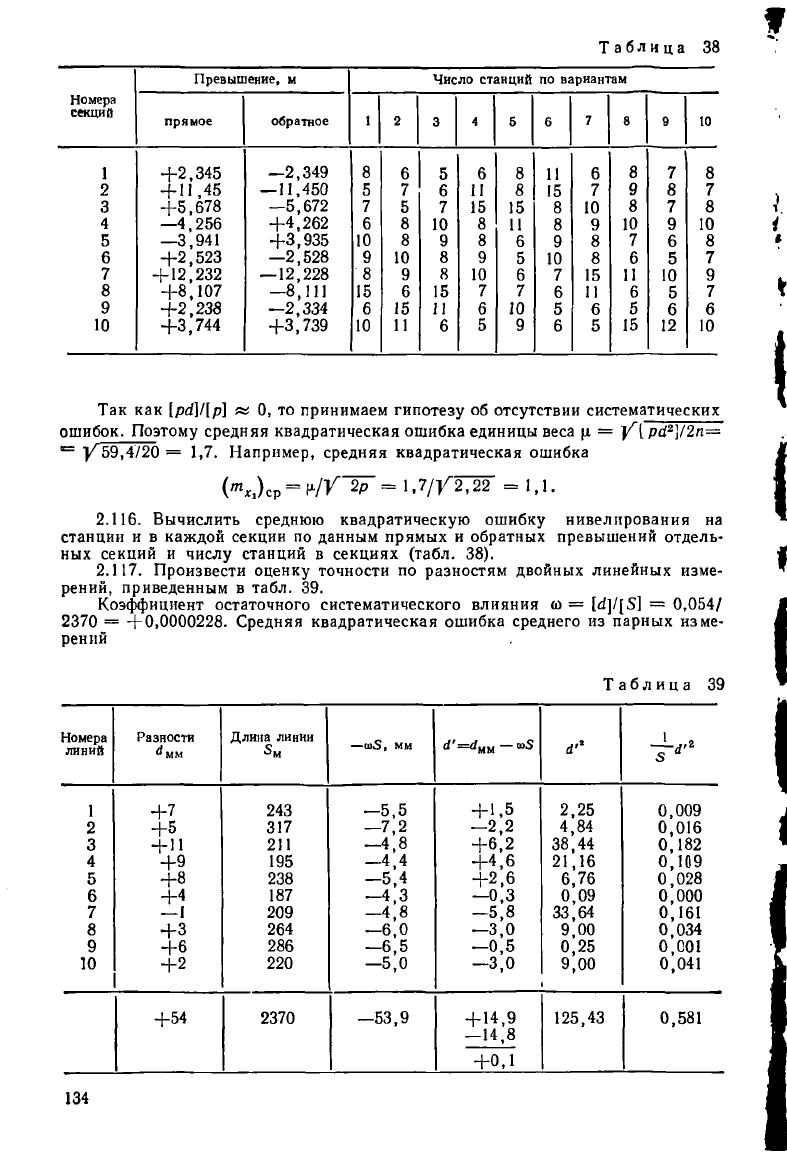
Таблица 54'
Превышение, м
Число станций по вариантам
Номера
прямое обратное
'
2
3
4
5 6
7
8
9 10
1 +2,345
—2,349 8
6
5
6 8
11
6
8
7
8
2 + 11,45
—11,450
5 7
6 11
8
15
7
У
8 7
3
+5,678
—5,672
7
5 7 15
15 8 10
8
7 8
4
—4,256
+4,262
6 8
10
8
11 8 9
10
9 10
5
—3,941
+3,935
10 8
9
8
6
9
8
7
6
8
6
+2,523
—2,528
9 10
8
9
5 10
8 6
5
7
7
+12,232
—12,228 8
9
8
10 6 7
15 11
10
9
8
+8,107
—8,111 15 6 15
7 7
6 11
6
5
7
9
+2,238
—2,334
6
15
11
6
10
5 6
5
6
6
10
+3,744
+3,739 10
11
6
5 9
6 5
15 12
10
Так как [рй]/[р] « 0, то принимаем гипотезу об отсутствии систематических
ошибок. Поэтому средняя квадратическая ошибка единицы веса р, = ~у
г
[рсР]12п—
У 59,4/20 = 1,7. Например, средняя квадратическая ошибка
К,)ср = = 1.7/^2722- = 1,1.
2.116. Вычислить среднюю квадратическую ошибку нивелирования на
станции и в каждой секции по данным прямых и обратных превышений отдель-
ных секций и числу станций в секциях (табл. 38).
2.117. Произвести оценку точности по разностям двойных линейных изме-
рений, приведенным в табл. 39.
Коэффициент остаточного систематического влияния ш = №]/[5] = 0,054/
2370 = +0,0000228. Средняя квадратическая ошибка среднего из парных изме-
рений
Таблица 39
Номера
линий
Разности
а
ым
Длина линии
5м
—ш5, мм
а'*
1
+7
243
-5,5 +1,5 2,25
0,009
2
+5
317
-7,2 -2,2 4,84
0,016
3
+ 11 211
-4,8
+6,2 38,44
0,182
4 +9
195
—4,4
+4,6
21,16 0,109
5
+8
238
-5,4
+2,6
6,76 0,028
6
+4
187
—4,3 -0,3 0,09
0,000
7 —1
209
—4,8 —5,8 33,64
0,161
8 +3
264 —6,0
—3,0 9,00
0,034
9 +6
286 -6,5 —0,5
0,25
0,001
10
+2
220 —5,0 —3,0
9,00
0,041
+54
2370
—53,9
+ 14,9
—14,8
+0,1
125,43 0,581
134

/
П77Т
5
а
1 /"0,531
Коэффициент случайного влияния Ц! (средняя квадратическая ошибка на
1 м), относящийся к среднему значению из обоих измерений и выраженный в
метрах, будет ц
х
= 0,001 ц
С
р = 0,000127.
2.118. С помощью таблиц нормально распределенных случайных величин
смоделировать разности двойных измерений (» = 1, 2...15) со с. к. о. а^ =
= 1 + 0,1« и постоянной систематической ошибкой с
}
= 0,5.
Проверить гипотезу о наличии систематической ошибки по формуле (2.140),
вычислить ошибку единицы веса и (т
Х[
)
ср
по формуле (2.136). В качестве а
и
при-
нять о^ = 8.

Часть II.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Глава 3.
ПАРАМЕТРИЧЕСКИЙ СПОСОБ УРАВНИВАНИЯ
§ 27. ОБЩЕЕ ПОНЯТИЕ О МЕТОДЕ НАИМЕНЬШИХ КВАДРАТОВ
В теории ошибок измерений мы рассматривали вопрос математи-
ческой обработки результатов многократных измерений одной и той
же величины. Эта задача является частным случаем совместной обра-
ботки совокупности результатов измерений многих величин, напри-
мер, превышений в нивелирных, длин сторон и углов в плановых
сетях и др.
В геодезической практике число выполненных измерений п всегда
больше числа тех измерений к, которые следовало бы сделать, чтобы
получить искомые величины (необходимые неизвестные). Измерения,
которых было бы достаточно для определения этих неизвестных, на-
зовем необходимыми. Разность г = п — к называется числом избы-
точных измерений. Так, в полигонометрическом ходе выполнено п
3
измерений длин сторон и = п
3
+ 1 измерений углов (всего 2п
5
+
+ 1 измерений), а число необходимых измерений, очевидно, равно
удвоенному числу определяемых пунктов (для каждого пункта необ-
ходимо получить две координаты х и у), т.е. 2 (п
д
— 1), поэтому
г = 2п
3
+ 1—2 (п
5
- 1) = 3.
В сети триангуляции, изображенной на рис. 38, для определения
координат трех пунктов (пункты А, В, С, О, Е приняты исходными,
безошибочными) измерен 21 угол, так что г = 21 — 6 = 16. В ниве-
лирной сети (рис. 39) г = 5 — 2=3. Наличие избыточных измерений
позволяет повысить точность искомых величин, выполнить оценку точ-
ности самих измерений и надежно их проконтролировать.
С наличием в геодезической сети избыточных измерений связана
задача уравнивания. Ясно, что в этом случае искомые неизвестные
1
РИС. 38
рис. 39
136.

определяются неоднозначно и зависят аг того, по каким измерениям
они вычисляются. Задача уравнивания и заключается в том, чтобы,
используя все измерения, получить однозначно все неизвестные.
Получение наиболее надежных значений этих величин и их оценка
точности составляют задачу так называемых уравнительных вычис-
лений (уравнивания). Уравнивание выполняют по методу наимень-
ших квадратов (м. н. к.), согласно которому смеренные величины
получают поправки VI, удовлетворяющие условию [/н
2
] = т
;
п, где
р
{
— вес измерений. К. Гауссом и русским математиком А. Марко-
вым доказано, что этот принцип приводит к наилучшим оценкам ис-
комых цеизвестных: они при отсутствии систематических ошибок в
измерениях являются несмещенными и обладают минимальной дис-
персией (теория Гаусса — Маркова). Это утверждение справедливо
и для любых функций уравненных неизвестных. При этом не требу-
ется, чтобы результаты измерений подчинялись нормальному закону
распределения. Однако в последнем случае, который наиболее часто
встречается в геодезической практике, при уравнивании по методу
наименьших квадратов уменьшается риск того,что найденные оценки
в своей совокупности будут существенно отклоняться от истинных
значений. Только при нормальном законе становится возможным по-
строение доверительных интервалов с использованием распределении
Стьюдента и х
2
-
Существуют два основных способа уравнивания: параметрический
и коррелатный (ранее они назывались сс ответственно способами
посредственных и условных уравнений). В первом способе из решения
так называемых нормальных уравнений получают непосредственно
уравненные значения искомых величин — параметров, а во втором —
сначала вспомогательные множители — так называемые коррелаты,
а затем искомые величины п их функции. Оба способа уравнивания
приводят к одинаковым результатам, но часто обладают различной
трудоемкостью при решении одной и той же задачи. Так, например,
при уравнивании полигонометрического хода, имеющего 10 опре-
деленных пунктов, параметрическим способом придется совместно ре-
шать 20 уравнений, а при коррелатном способе, как мы видели выше,
всего 3. Следует, однако, иметь в виду, что число совместно решаемых
уравнений, если задача решается на ЭВМ, не является определяющим
критерием выбора того или иного способа уравнивания. Нужно учи-
тывать также простоту составления исходных уравнений.
Кроме указанных двух способов уравнивания, существуют и так
называемые комбинированные способы, сочетающие достоинства од-
ного и другого.
Рассмотрим кратко основные положения параметрического спо-
соба уравнивания.
§ 28. ПАРАМЕТРИЧЕСКИЙ СПОСОБ УРАВНИВАНИЯ, УРАВНЕНИЯ
ПОПРАВОК, НОРМАЛЬНЫЕ УРАВНЕНИЯ (РАВНОТОЧНЫЕ ИЗМЕРЕНИЯ)
Пусть в качестве параметров (необходимых неизвестных) выбраны
к величин, точные значения которых обозначим через X} ц — 1, 2
137.

Эти неизвестные не должны быть связаны между собой функциональ-
ными зависимостями. Заметим, что в качестве X] могут быть выбраны
также к измеренных величин, позволяющих однозначно определить
искомые величины, т. е. те величины, ради получения которых и вы-
полняются геодезические измерения. Например, в нивелирной сети
(см. рис. 39) в качестве X] можно выбрать отметки узловых точек
#1 и Н
2
. Так обычно и поступают. Но можно было бы принять Х
1
—
= к
и
Х
2
= /г
4
, где к) — истинные значения превышений по ходам
1 к 4.
Истинные значения результатов измерений У
(
(I — 1, 2, ..., п)
и параметры X], очевидно, должны быть связаны уравнениями вида
= Ч,(Х
1г
Х„ ..., Х
п
). (3.1)
причем здесь п к.
Систему уравнений (3.1) называют исходной системой связи. Так
как истинные значения У
{
нам неизвестны, то нельзя определить и
точные значения X]. Однако в силу переопределенности исходной
системы вместо У
{
и X) можно подобрать так называемые уравненные
значения у
1
и х
{
, такие, что
У1 = Ч>(*1. х
г
, ..., х
к
), (3.2)
причем у
{
= у] + VI, где у'{ — измеренное значение функции, а
VI — поправка.
Систему уравнений (3.2) необходимо привести к линейному виду.
Разложив для этого функции Ф^АГЬ ЛГ
2
, ..., х
к
) в ряд Тейлора и ограни-
чиваясь линейными членами разложения, получим
у'
{
+ VI = + Ь^х
2
+ ... + ёг
ь
Ч + <р(х!°\ х%
0)
,..., хЦ
0)
)
или
VI = а^х, + + ... + д
{
Ьх
к
+ 1
{
, (3.3)
где свободный член
= .:,хП-у'г, (3.4)
здесь х/
0>
— приближенные, однако близкие к точным значения пара-
метров. Их обычно вычисляют по измеренным значениям у'.
Первое слагаемое в формуле (3.4) представляет приближенное значе-
ние функции. Коэффициенты а|, Ь
{
в формуле (3.3) суть частные
производные
= , Ь, = (Щ , = , (3.5)
взятые по уравненным значениям параметров, но вычисленные при
их приближенных значениях.
Уравнения вида (3.3) называют системой параметрических урав-
нений поправок (уравнений поправок).
Если исходная система (3.1) имеет линейный вид, то уравнения
138.

РИС. 40
РИС. 41
поправок также имеют вид (3.3), при этом коэффициенты а Ь
(
, ..., §
г
равны коэффициентам при неизвестных X] в этих уравнениях. В этом
случае из .уравнения можно было бы сразу находить неизвестные X).
Однако эти значения, как правило, имеют большое число значащих
цифр. Поэтому с точки зрения точности вычислений и в линейном
случае находят не х
}
, а поправки 8х].
Коэффициенты уравнений поправок обозначают часто и одной бук-
вой с двумя индексами — а а свободный член а
!о
. Тогда вместо
(3.3) можно написать
= а^*! + а
12
Ьх
2
+ ... + а
1к
Ъх
к
+
Первый способ обозначений исходит еще от Гаусса, он стал клас-
сическим и традиционно употребляемым в геодезии, хотя имеет недо-
статок, связанный с ограниченным числом букв в алфавите (что, впро-
чем, не является препятствием для его применения). Недостаток вто-
рого способа — в двойной индексации.
3.1. Составить уравнение поправок для нивелирного хода с номером I,
проложенного между двумя узловыми реперами (рис. 40).
Решение. Обозначив через Х
иач
и Лк
0Н
истинные значения отметок, мож-
но написать исходное уравнение связи вида
— -Хкон—-^нач* (3-6)
Хотя это уравнение имеет линейный вид, можно далее выполнить формально
его линеаризацию. Тогда получим
=
1. = — 1, = *кон — *нач — У1
и
Щ = й*
кон
— »*„ач + к
•
'(3.7)-
Заметим, что если исходное уравнение связи линейное, коэффициенты урав-
нений поправок не зависят отд^
0)
.
3.2. Получить уравнение поправок для стороны 5,-, измеренной между двумя
пунктами (рис. 41) плановой сети.
Решение. Исходное уравнение связи имеет вид
5= {Хв-ХА? + (УВ-УА? ,
где X и К — координаты точек.
Далее находим коэффициент
139.

в
РИС. 42
РИС. 43
где Од — дирекцнонный угол стороны в направлении от А к В, вычисленный по
приближенным координатам у^, у^. Свободный член
Окончательно имеем
= — СОза/В
ж
—зша^Ву -(-соз + 51па(8у ,
л
,-„
л
, ,
3.3. Составить уравнение поправок для дирекционного угла
Ответ:
(3.8)
(3.9)
«( стороны
*>
а(
= — (81па,»*
д
— соз— 5Ш«<»*
В
+со$ а
{
Ьу
в
) + 11, (3.10)
где
> * Ау
0
(3.11)
3.4. Сделать то же самое для угла {$, измеренного на пункте А между пунк-
тами В и С.
Ответ: о = о_ —о_ +/, 1=1 —I
9 о _ а
1
• с • .
Р
АС АВ АС АВ
(3.12)
3.5. Составить уравнение поправок для направления с пункта А на пункт
В (рис. 42).
Так как направление N есть угол между стороной АВ и нулевым диаметром
' лимба, то можно написать
0
Ы
=
°шАВ-".«Ч-
Используя результат решения задачи 3.3, получим
0аг
= _«а<°>-Н
АВ
+ 1,
где
•Дж
(3.13)
(3.14)
АВ
Величину а
<0)
называют ориентирующим углом (дирекцнонный угол нулево-
го диаметра лимба).
3.6. Составить уравнение поправок для стороны трилатерации, если 5 =•
= 1635,580 м.
= Д*<°>= 1315.540 м; Ду™ = =
= 971,806 м; / = 0,021 м.
140.

Ответ: а = 0.8046*,, + 0,5946у
А
— 0,8046*
В
— 0,5946у
в
+ 0,021.
3.7. Составить уравнение поправок для дирекционных углов двух сторон
(см. рис. 42), если измеренные значения а
лв
= 182°1Г03,5", а
АС
= 253 39'59,9".
40 120,047, </<°> = 36 999,739,
= 39 022,182, ^= 36 957,868,
4°>= 39 679,750, у^ = 35 497,296,
5$= 1099; 5$= 1566.
Ответ: VI =— 7,16 8*,, + 187,60 8у„ + 7,16 8х
в
— 187,60 Ьу
в
+ 1
АВ)
АВ
где 1
ав
= — 0,7".
°*
АС
=— 126,43 8*^ +37,05 Ьу
А
+ 126,43 8*
с
—37,05^
с
+1
АС
,
где 1
ас
= — 0,3".
3.8. Сделать то же для угла САВ.
Указание: угол представить как разность дирекционных углов.
3.9. Составить уравнение поправок для нивелирного хода (рис. 43), если
х
(
и
% = 100,000; 4он = 149,550; у = 49,545.
О т в е т: о = 6х
кон
— 6х
нач
+ 0,5 см.
3.10. Из измерений получены значения углов плоского треугольника у, =
= 61°17'35", у
2
= 55°39'27", у
3
= 63°02'52".
По этим результатам составить уравнения поправок для определения урав-
ненных значений всех трех углов х, у, г.
Решение. В данной задаче из трех неизвестных х
х
, х
2
, х
3
два будут не-
зависимыми, а третье — их функцией. Выбрав в качестве независимых неизвест-
ных х
х
и дс
а
, напишем исходное уравнение связи х
3
= 180° — (х
1
+ х
а
).
По числу измерений составим три уравнения поправок:
лг, — 61° 17'35" = х
г
— 55°39'27" = и,;
180° — (*, + х
2
) — 63°02'52" =
Для облегчения вычислений введем приближенные значения неизвестных.
Тогда
XI = 61°17'35" + Ъх
г
\ х
г
= 55°39'27" + 8ЛГ
2
;
+ х
2
= 116°57'02" + 8*
(
+ 8*,.
Теперь уравнения поправок примут вид
8ж, . . . =о
х
;
8*, . . . = о
2
;
— Ъх
х
— Ьх
г
+ 6" = V
3
.
3.11. Составить уравнение поправок измерений длины окружности и площа-
ди круга, выполненных для определения радиуса окружности.
Решение. Исходная система связи будет
у
х
= 2Я#; у
г
= ТЕ/?
2
;
коэффициенты уравнений поправок
""©Г
2
*
141.

\с
РИС, 44
где #(0>— приближенное значение радиуса; свобод-
ные члены
= 2тс/?<°> _ 1
г
= пК
(0)
* -у
г
.
Уравнения поправок
V
^
= а,ог + у
2
= а
2
Ьг + 1
г
.
3.12. Составить уравнения поправок, возни-
кающие при уравнивании нивелирной сети (рис.
44), если: а) в качестве необходимого неизвестного
принять превышение по ходу 1, б) отметку узловой
точки.
Решение. Пишем исходные уравнения связи
У1
= Х;
Уг
= -Х-Н
д
+Н
с
у
3
= Х+Н
А
+Н
В
и уравнения поправок
= + о
2
= —6дс+/
г
;
с
3
= Ьх + /
3
,
где
Уз-
= *<°>- - *<°>- Н
А
+ Н
с
- у
2
; /
3
= Н
А
+ Н
ь
В качестве х<°> целесообразно принять измеренное превышение у у. Тогда /
х
=
= 0.
Ответ: б) = Ьх + V
г
=—Ъх + 1
г
, а
3
= Ъх + /
3
,
где /, = 0. 1
г
= Н
0
-( х
(0)
+у
г
), 1
3
= х
т
-(Н
в
+ у
3
)
при х™=Н
А
+у
±
.
Переопределенную систему уравнений поправок в случае, когда
измерения равноточны, решают под условием метода наименьших
квадратов Ф = [у
2
] = гтмп.
Для отыскания минимума функции Ф необходимо найти ее частные
производные по неизвестным и приравнять их нулю. В результате
получают систему линейных уравнений (в буквенной форме записи)
1 дФ V"! до
{
. .
п
1=1
= = [Щ = 0;
2 дх
г
^ дх
%
'
I -= 1
2 дх
к
^
1
дх
к
16 ^
(3.16)
142.
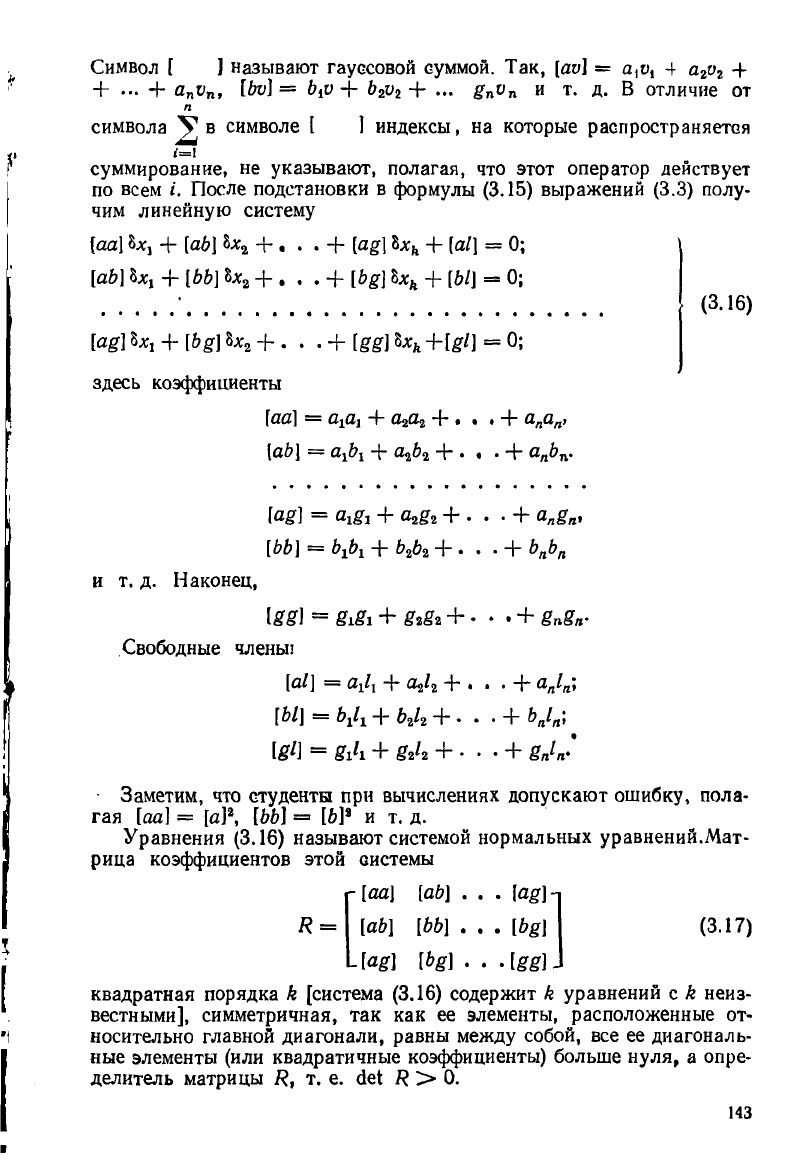
Символ [ ] называют гауссовой суммой. Так, [да] = а,о, 4 А
Г
V
Г
+
+ ... 4- а
п
а
п
, [Ьо] = 4- Ь
2
а
2
4- ... ёп*>п и т. д. В отличие от
п
символа V в символе [ ] индексы, на которые распространяется
(=1
суммирование, не указывают, полагая, что этот оператор действует
по всем I. После подстановки в формулы (3.15) выражений (3.3) полу-
чим линейную систему
[aa] Ьх, + [аЬ] Ъх
г
+ . . . + [а^] Ьх
ь
+ [а1] = 0;
[ab] Ьх
х
+ [ЬЬ] 8*, + . . . + [Ь
8
] Ьх
к
+ [Ы] = 0;
Ш ^ + + . . . + Ьх
к
+[*/] = 0;
здесь коэффициенты
[aa] = а
х
а
х
4- а
2
а
2
+ • . • +
а
п
а
п'
[ab] = аф
г
+ аф
г
+ . , . 4- а
п
Ь
п
.
(3.16)
\аё] = +
а
гёг 4-... 4- а„8п'
[ЬЬ] = ЬА + Ьф
2
+ . . . 4- Ь
п
Ь
п
и т. д. Наконец,
= 8181 + 8*8% + • • • + 8п8п-
Свободные члены:
[а1] = а
у
11 + аА 4-. • • 4- а
л
/„;
[Ы\ = 6Л + Ь
2
к 4- • • • 4- Ъ
п
1
п
\
\ё
1
\ = ёА + + • • • + ёп
1
п'
Заметим, что студенты при вычислениях допускают ошибку, пола-
гая [аа] = [а]
2
, [ЬЬ] = [&]* и т. д.
Уравнения (3.16) называют системой нормальных уравнений.Мат-
рица коэффициентов этой системы
Я =
р [аа] [аЬ] . . .
[а^т]
-|
[аЬ] [ЬЬ] . . . [Ьц]
-[аё] [Ьё\ . .
(3.17)
квадратная порядка к [система (3.16) содержит к уравнений с к неиз-
вестными], симметричная, так как ее элементы, расположенные от-
носительно главной диагонали, равны между собой, все ее диагональ-
ные элементы (или квадратичные коэффициенты) больше нуля, а опре-
делитель матрицы Н, т. е. <1е1 Н > 0.
из.
