Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

3.21. Будет ли являться нормальной матрица Н=А

А,

если матрица

1 0 2

1 1 2

А=\

1 1 2

1 0 2

Ответ: нет.

3.22. Составить уравнение поправок, нормальное уравнение и оценить

точность уравненного неизвестного в общем виде для случая я-кратного измере-

ния одной и той же величины. Доказать, что * = [х]1п, р

= л, а также х = *„+

+ [е]1п (см. § 21).

3.23. Дана матрица весовых коэффициентов уравненных координат х

А>

*в> У В

0,979 —0,559 0,750 —0,413%

0,875 —0,430 0,270

' 0,780 —0,430

0.870У

Найти все шесть коэффициентов корреляции между уравненными координатами.

Ответ: г^ =0,604; ^ ^=0,858; г

Хл

= — 0,447;

УАХв

=0,т-, Г

УаУв

=0,289; г

ХвУв

=0,552.

§ 31. ОЦЕНКА ТОЧНОСТИ ФУНКЦИЙ УРАВНЕННЫХ

НЕИЗВЕСТНЫХ

Одной из важных задач, которую часто приходится решать при

выполнении уравнительных вычислений, является оценка точности

функций уравненных неизвестных х

}

(уравненной функции)

Р = ДХр ...

Возможны два способа ее решения.

Способ 1. Если известна матрица ф весовых коэффициентов,

то обратный вес уравненной функции

/Р

=}<2р (3.49)

или в подробной записи

где матрица-строка

/ = (/х. к /А) (3.51)

составлена из частных производных

''-(Иг)

дХ

1>Х, = х,-

164.

Для случая 6 = 3 вместо формулы (3.50) подробно будем иметь

= Сц + +

+ 2Ш

1г

+ 2/^.

Так, в задаче 3.17 обратный вес суммы уравненных углов Р =

= х

{

+ х

(шестой угол) найдем, учитывая, что все [

= 1,

/Р

= 0,5 + 0,5 + 0,5 + 2 (— 0,250 — 0,250) = 0,50.

В матричной форме согласно формуле (3.49) получим тот же ре-

зультат

(

0,50 —0,25 0

—0,25 0,50 —0,25

0 —0,25 0,50

= (0,25 0 0,25)•(! 1 1)

= 0,50.

Заметим, что матричную форму (3.49) удобно применять, когда

оценивается не одна, а сразу несколько, пусть т, функций. В этом

случае матрица / имеет размер т X 6, причем каждая ее 1-я строка

соответствует 1-й функции и составляется согласно (3.51). В этом слу-

чае в левой части выражения (3.49) вместо обратного веса

следует писать матрицу обратных весов системы функции (вектор-

функции).

Например, если оценивается точность двух функций

Р^ — х1 + х

; Р

= х

+ х

— уравненных углов 4 и 6 (см. рис. 46), то получим

0,50 —0,25

0г —0,25 0,50

0 —0,25

/0,25 0,

\0,25 0

25 —0,25

Матрица симметричная. С ее помощью находим коэффициент

корреляции

- —- 0,5.

Ко,50 Ко,50

165.

Частным случаем оцениваемых функций являются уравненные

результаты измерений (уравненные измерения). В этом случае для у(

будем иметь коэффициенты функции /

= а

, = Ь

(

, ..., =

а для совокупности всех уравненных измерений получим матрицу

обратных весов

От = = А<1А\ (3.52)

3.24. Применяя формулу (3.52), доказать, что 11р

. = 0,ц.

3.25. Дана матрица обратных весов '

0,75 0,40

0,40 0,90

уравненных отметок узлов нивелирной сети (см. рис. 40). Найти матрицу обрат-

ных весов всех пяти превышений.

Решение. Составляем матрицу коэффициентов уравнений поправок со-

гласно (3.7)

А = . (3.53)

Далее согласно формуле (3.52) находим

0,75 0,40'

0,75 0,40

А(}= | —0,35 0,50

0,40 0,90

0,40 0,90,

ЖМ

П 1 —1 0 0

10 0 111

'0,75 0,75 —0,35 0,40 0,40'

0,75 —0,35 0,40 0,40

0,85 0,50 0,50

0,90 0,90

0,90

3.26. Найти обратные веса уравненных дирекционного угла и длины сторо-

ны триангуляции между пунктами 1 и 2 , если Оц = 90°, 5 = 2063 м, а матрица

весовых коэффициентов координат пунктов лх

0,320 —0,050

0,765

<Э

= "

0,250 0,005\

0,010 0,750

0,298 —0,010

0,900 .

Вычислить средние квадратические ошибки та и т

, если ^ = 0,02 м.

Указание. Коэффициенты функций составить согласно выражениям

(3.10) и (3.9).

166.

1 1

Ответ! ~р~ -» 660, р = 0,155, т

= 0,5", т

= 0,01 м.

а <5

Способ 2 (способ дополнительного столбца). Если весовые

коэффициенты неизвестны, то применяют формулу

в которой }

= 0,

[/.• I]

Л+1

[аа]

[ЬЬЛ]

И1к

Цк-(Ь — 1)]

ГйМб-1)!

(3.54)

[/з-2] =

1/.-1] =/,

МП

[аа]

Если условно обозначить

[а/] = Л;

[Ы] = /,;

Ш] =

№ = /*

1 = 0,

[аа] '

[Ьс.1][[

.1]

[ЬЬ. 1]

И Т. Д.

(3.55)

то алгоритм Гаусса [/ь+1-6] раскрывается так же, как и [П.к]. Алго-

ритмы [/

.1], [/а.2], ..., [/ь-(6—1)] раскрываются так же, как и алго-

ритмы [6/.1], [с1.2], ..., [&1.(к—1)], если иметь в виду обозначения

(3.55).

Легко понять теперь, что алгоритм МРр можно получить в схеме

Гаусса, если в нее ввести дополнительный столбец свободных членов

(3.55). Сделав в нем те же преобразования, что и в основном столбце

свободных членов /, в результате получим алгоритм

. условно

Для контроля вычислений служит формула

[Д..

[/,.11

[аа]

[ЬЬ. 1]

-7Г = 12Л+1-Л] = [/]

[**• (6-1)1 Цк-(*-!)]

[М-(*-!)!

в которой вновь введены суммы

21 = 108] —+

2, ~[Ьз] -[Ы] + к,

2»-М-[«7/1 + /».

(3.56)

167.

Таблица 54'

1,00

-0,333

7,00

—2,333

0,33

—0,124

4,33

— 1,622

0,51

—0,254

2,51

—1,249

—1

!Р

—0,50

—0,51

Для раскрытия алгоритмов с символом 2 следует условно считать,

что

2! = 1051, 2, = №, . . •, 2» = 2Й

1 = 1/1- (3.57)

Тогда алгоритм будет раскрываться так же, как и [&.А],

условно

т.е. ИРр = [/5.й], а алгоритмы [2

.1], [2

.2], .«-., 1)] — как

алгоритмы [&5.1], [сх.2], ...,

[§1.(к—1)],

если учитывать обозначения

(3.55) и (3.57), например

ЕгП-й-ЙйЬ.

(\ЬзЛ])

2] = ^ - мь _ ЫЫ. „

. д.

' ^ \аа] [66.1]

([С5. 2])

Найдем обратный вес функции в задаче 3.17. Добавив в схему

Гаусса два дополнительных столбца / и 2 и выполнив их преобразо-

вание, получим (табл. 45), обратный вес — .

Подобным образом в схеме Гаусса можно оценивать точность сразу

нескольких функций.

§ 32. ЗАДАЧИ НА УРАВНИВАНИЕ РАВНОТОЧНЫХ

ИЗМЕРЕНИЙ

3.27. Выполнить уравнивание дирекционных углов в сети триангуляции

(рис. 46). Оценить их точность и точность уравненного угла = <х

— а,. Ис-

ходные дирекционные углы: <х

ол

= 0, а

ов

= 135°40'19,5"

Измеренные углы приведены в табл. 46.

168

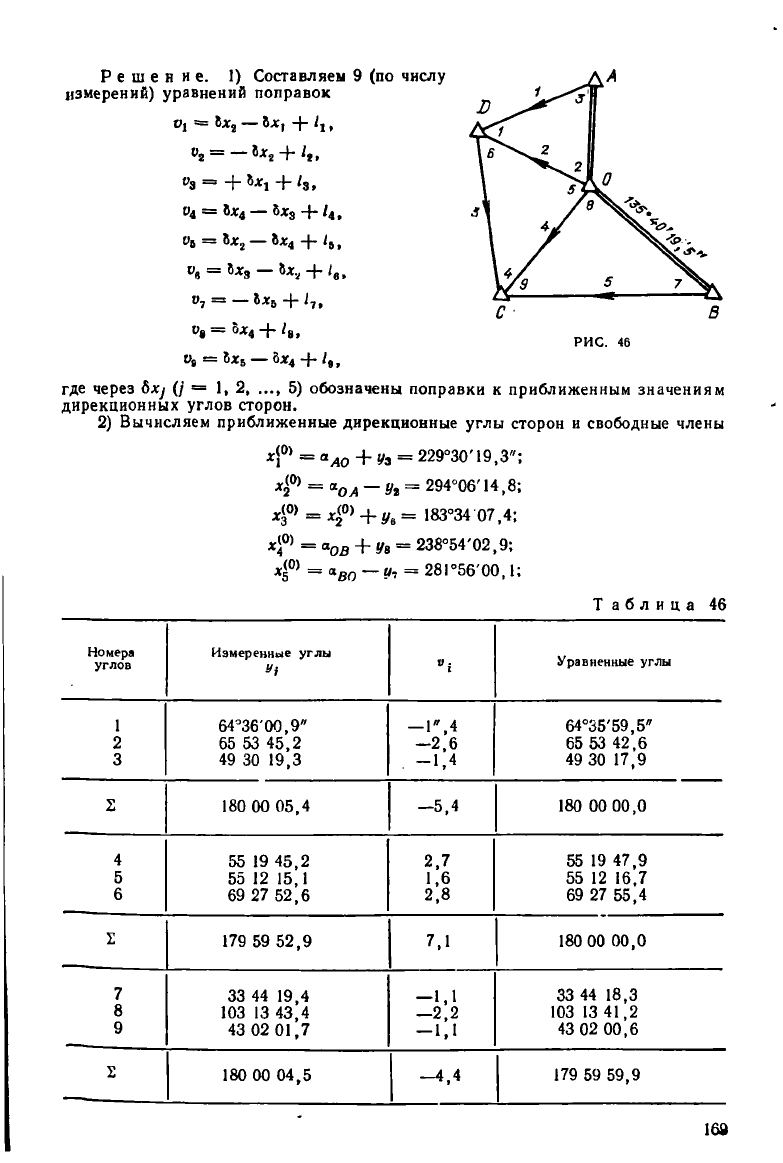
Решение. 1) Составляем 9 (по числу

измерений) уравнений поправок

о, = _ Ьх, + /,,

= — 8*

+ /„

»э = + + 'з,

= 8*

— 8*3 + /

= 8*

— 8*

+ /

= ®*з —

ъх*

+ и.

», = — 8*

+ /

V, = 8*5 — 8*4 +

где через &x^ (/ = 1, 2 5) обозначены поправки к приближенным значениям

дирекционных углов сторон.

2) Вычисляем приближенные дирекционные углы сторон и свободные члены

= а

А0

+1/

= 229°30'19,3";

0А ~Уг = 294°06'14,8;

*<°> = *<°> + у, = 183°34 07,4;

ов +

Ув

~ 238°54'02,9;

РИС. 46

-(О) = ,

во"

и, = 28Г56'00,1;

Таблица 46

Номера

углов

Измеренные углы

У)

Уравненные углы

64°36'00,9"

65 53 45,2

49 30 19,3

—Г,4

-2,6

. -1,4

64°35'59,5"

65 53 42,6

49 30 17,9

180 00 05,4

-5,4

180 00 00,0

55 19 45,2

55 12 15,1

69 27 52,6

2.7

1,6

2.8

55 19 47,9

55 12 16,7

69 27 55,4

179 59 52,9

7,1

180 00 00,0

33 44 19,4

103 13 43,4

43 02 01,7

—1,1

-2,2

-1,1

33 44 18,3

103 13 41,2

43 02 00,6

180 00 04,5 -4,4

179 59 59,9

166.

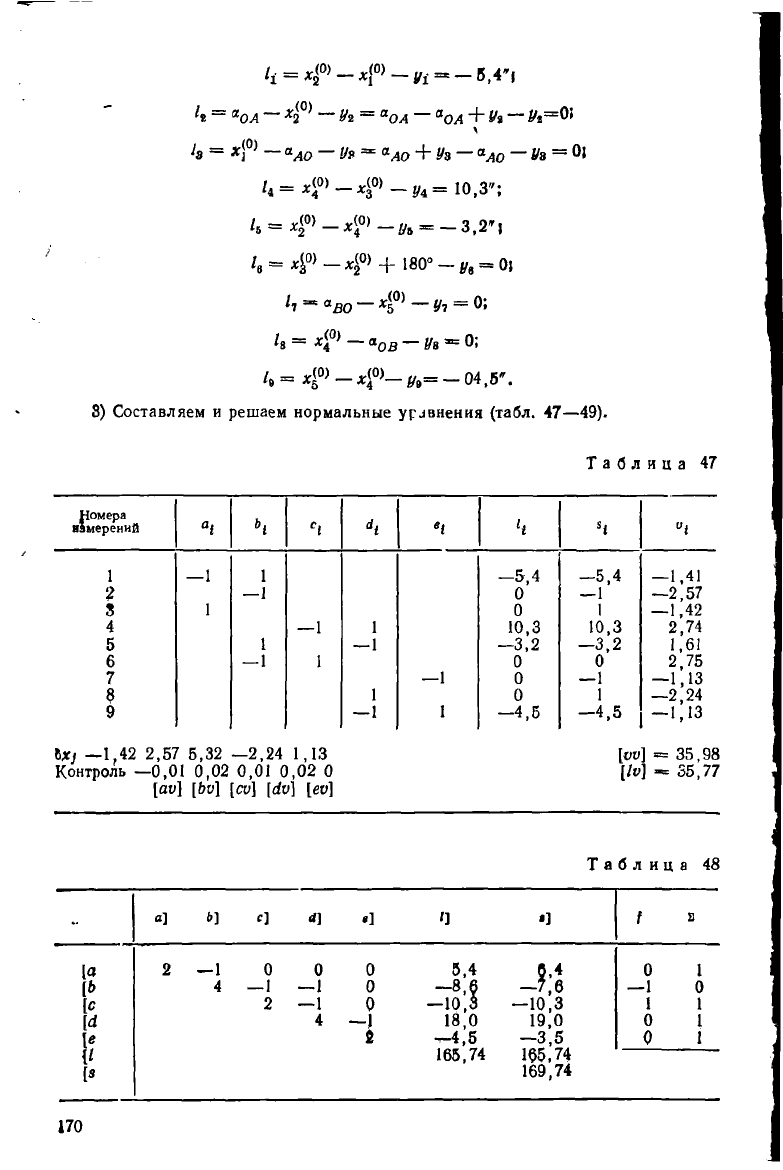
/< = ,(<»_*<<»_„. = _ в,4»,

'г =

0А — *2

—

У%

ол —

ол + й — й=0»

'з - *1

—

А0 — у» = «ЛО + Уз—

А0—Уз = °1

= *<<»- 4°)- </

= 10,3";

= -3,2»«

'в = 4

- 4

+ 180° -

{/,

= 01

'!-«ЛО-*8

—й =

'в = *4

— «ов —

Ув

= 0;

8) Составляем и решаем нормальные урлвнения (табл. 47—49).

Таблица 47

Номера

измерений

°1

1 —1 1 -5,4 —5,4

—1,41

2 —1

—1

—2,57

1 —1,42

—1 1 10,3

10,3

2,74

—1 —3,2

-3,2

1,61

—1

1 0

0 2,75

—1 0 —1

-1,13

1 —2,24

—1

—4,5

-4,5

-1,13

Ьх) —1,42 2,57 5,32 —2,24 1,13 [от] = 35,98

Контроль —0,01 0,02 0,01 0,02 0 [/ч] 35,77

[ау] [Ьо] [СУ] [Л] [ео]

Таблица 48

а] Ь] с]

«]

1а

2—1 0

0 0

3.4

0 1

4 —1

—1 0

-8,6

-7,6

—1

1С

2 —1

—10,3 —10,3 1

-1

18,0

19,0 0

[О

-4,5 —3,5

165,74

195,74

165,74

169,74

170.

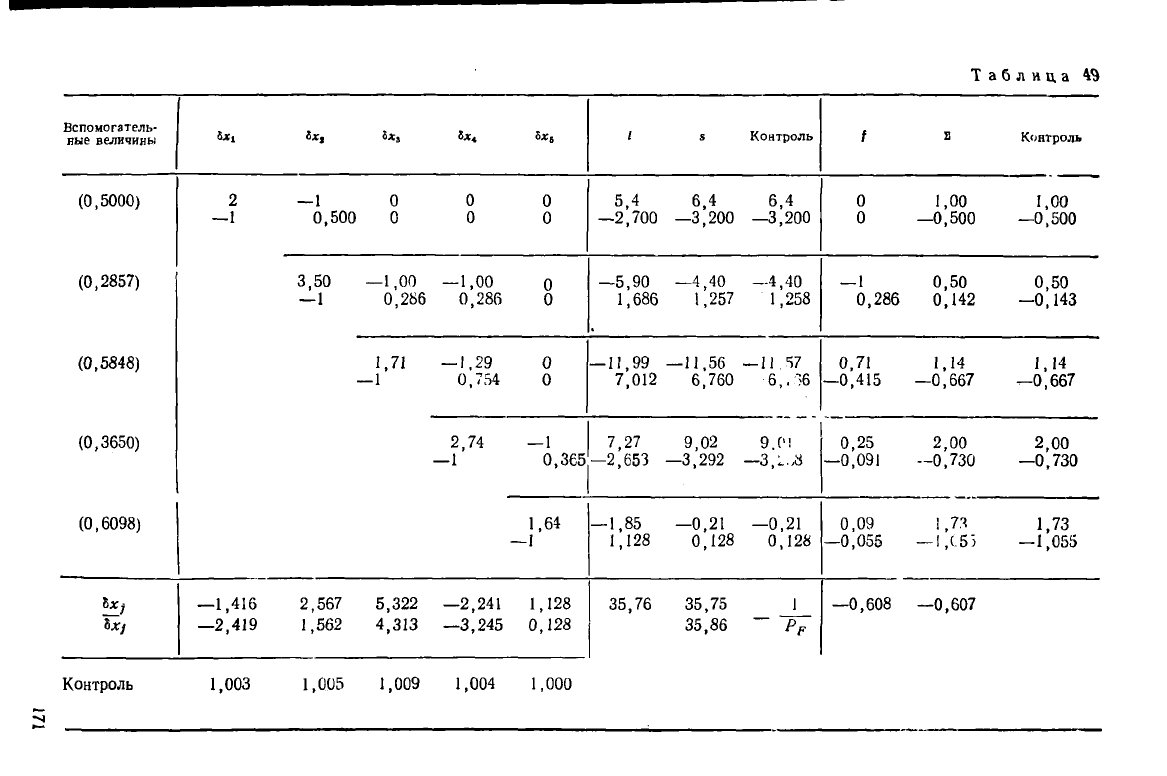
Таблица

168

Вспомогатель-

ные

величины

5*1

г*»

6*5

1 5

Контроль

(0,5000)

— 1

0,500

5,4

—2,700

6,4

—3,200

6,4

—3,200

1,00

—0,500

1,00

—0,500

(0,2857)

3,50

—1

—1,00

0,286

—1,00

0,286

—5,90

1,686

—4,40

1,257

—4,40

1,258

— 1

0,286

0,50

0,142

0,50

-0,143

(0,5848)

1,71

-1

— 1,29

0,754

— 11,99

7,012

—11,56

6,760

— 11.57

•6,.";6

0,71

—0,415

1,14

—0,667

1,14

—0,667

(0,3650)

2,74

—1

0,365

7,27

-2,653

9,02

—3,292

9.0!

—3,1.,3

0,25

—0,091

2,00

-0,730

2,00

—0,730

(0,6098)

1,64

—1

— 1,85

1,128

—0,21

0,128

—0,21

0,128

0,09

—0,055

1,73

—

,(.55

1,73

—1,055

Ъх]

Ьх]

—1,416

—2,419

2,567

1,562

5,322

4,313

—2,241

—3,245

1,128

0,128

35,76 35,75

35,86

—0,608

—0,607

Контроль

1,003 1,005 1,009 1,004 1,000

Продолжение табл. 49

Матрица О получена по способу Ганзена.

Контроль

«и

<4/

1,000

0,6114

0,2228

0,16777

0,1117

0,0486

1,003

0,2228

0,4455

0,3354

0,2235

'0,0971

1,0044 0,1677

0,3354 | 0.8375

0,3352 0,1676

1,0035

0,1117

0,2235

0,3352 I 0,4462

0,2226

0,9970

0,0486

0,0971

0,1676

0,2226

0,6098

Заметим, что матрицу коэффициентов нормальных уравнений в этой задаче

можно обратить в общем виде

11 4 3 2 1 \

8 6

4 2 \

6 3 =

8 4 1

П I

0,1667

0,1111

0,0556

0,3333

0,2222

0,1111

0,8333

0,3333

0,1667

0,4444

0,2222

0,6111

0,6111 0,2222

0.4444

Как видно, обращенная в схеме Гаусса матрица <2 получена с точностью до

0,001.

4) Поправки VI вычислены и приведены в табл. 47. Как видно, контроли

[<го] = [М = ... = [ер] = 0 выполняются в пределах точности вычислений.

5) Вычисление уравненных углов у

{

с контролем выполнено в табл. (6 Вы-

полняется также контроль

Уг + Уь + Ув — ^ ЛОВ = 224°19'40,5" — ^ ЛОВ = 0.

6) Вычисляем уравненные дирекционные углы

= 229°30'17,9"; *

= 238°54'00,7";

= 294

06'17,4"

; х

= 281°56'01,2".

= 183°34'12,7";

7) Делаем окончательный контроль

172.

^ = х

— = 64°35'59,5"; у„ = *

— х

+ 180° = 69°27'55,3",

= а

д-*

= 65-5342,6"; у

= а

В0

-х

= 33°44'18,3";

Уз ~

/ —

А0 ~ 49

30'17,9"; у, = *

-а

ов

= 103°13'41,2";

щ — х± — х

= 55°19'48,0"; у^=х

— х

= 43°02'00,5".

= х

— *

= 55°12'16,7";

8) Выполняем оценку точности.

Средняя квадратическая ошибка измеренного угла

т = V [т\!{п — к) = Кзб/4 = 3".

Средние квадратические ошибки уравненных дирекционных углов:

т *

= т

Хб

=3 Ко,610 = 2,3";

= т

,= 3 Ко,446 = 2,0";

Хз

=3 1^0,837 = 2,7".

Средняя квадратическая ошибка функции

у«

= 3 = 3 Ко,61 = 2,3".

Обратный вес функции определен в дополнительном столбце схемы Гаусса

добавлением столбца (см. табл. 49)

а также по формуле

/=(0 —1 1 0 0)

— = $22 + Сзз — 2<г

з = 0,446 + 0,838 — 2-0,335 = 0,614.

у•

3.28. В табл. 50 приведены результаты измерения углов во всех комбина-

циях (рис. 47) в 30 вариантах. Уравнять эти углы параметрическим способом по

одному из вариантов и вычислить средние квадратические ошибки углов АОВ,

ВОС, СОО, ЭОЕ.

3.29. Уравнять дирекционные углы сторон триангуляционного построения

(рис. 48) по одному из следующих вариантов (табл. 51 и 52). Дирекционные

углы а

АВ

= 270°00'00,0", а

АЕ

= 102°56'57,5".

РИС. 47