Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений
Подождите немного. Документ загружается.


Если систему уравнений поправок (3.3) записать в матричной фор-
ме в виде
У = ААх + 1, (3.18)
где векторы
V, \ /
1
1 \ /
V = |
Ь =
I
, Дх = | Ьх
2
Ьх
ъ
а матрицу А — в виде
или
А =
пхь
А = |
пХк
(а
х
Ъ
х
. .
• * ^
• §2
\а
п
Ь
п
. .
• ёп )
а
и
а,
2
.
• • а
1к
^21 ^22 • • •
<*1к
уа
пХ
а
п2
соответственно в буквенной и индексной форме обозначений, то систе-
му нормальных уравнений получим путем умножения (3.18) слева
на транспонированную матрицу А
т
. Тогда
КАх + АЧ = А
Т
У — 0. (3.19)
Равенство
Л
Т
К = 0, (3.20)
которое представляет собой матричную форму уравнений (3.15), на-
зывают леммой Гаусса, или нормальными уравнениями в свернутом
виде.
Матрица
Н = А
Т
А (3.21)
имеет элементы (3.17) или в индексной форме
[а^Па,^] • . • Iа,а
[а
А
а
г
] [а
2
а
2
]
• («А ]
[о^ь] [а
2
а
й
] . . . [а
А
а
й
]
В этой же формуле выражения (3.15) или (3.19) записываются так|
|а,у| = а„о, + а
21
у
2
+ . . . + а
п1
р
п
= 0;
|а
2
у| = а
21
о
х
+ а.
1г
ь
г
+ . . . + а
гЛ
ь
п
= 0;
144.
= а
и
о, + а^о, + . . . + а^о» = 0.

Дальнейшая задача заключается в решении системы нормальных
уравнений.
При вычислении на ЭВМ вектор неизвестных часто получают в виде
Дл; = А
т
ь, (3.22)
где — так называемая обратная к Я матрица, такая, что =
= Я
1
Я = Е, где
/1 0 ... О
Е = ( 0 1 ... О
кХк I
\ 0 0 ... I
— так называемая единичная матрица.
Определение обратной матрицы связано с понятием ее определи-
теля. Определитель можно построить только для квадратных матриц.
Его обычно обозначают как |Л| или йе1 (Л).
Если в матрице А порядка п выделить какой-либо элемент а
1}
и
Еычеркнуть из нее ыо строчку и у-й столбец, то получается новая квад-
ратная матрица А' порядка (п—1). Ее определитель называется ми-
нором а
и
и обозначается М
11
^. Величина Ь
(
'/> = (—1)'+/ М
и
>'
)
назы-
вается алгебраическим дополнением а
1}
.
Справедлива формула
с!е1 Я = (3.23)
1=1
Если при помощи матрицы А составим новую матрицу .4* = [а*/],
где а,•/ = Б!
1
, называемую взаимной к А матрицей, то АА* =
= А* А = йе! (А)Е.
Если йе! (Л) =/= 0, то матрица А называется неособенной, невырож-
денной. Тогда можно составить матрицу А'
1
= (
1
/с1е1(Л)) • Л*, на-
зываемую обратной к Л.
Для матрицы второго порядка
'
а
\\ «12 ^
Л =
21 "22
)
I / а
м
—
обратная матрица
а-1 _ —
л
°11
а
22 —
а
и
а
г1 \—а
21
Например, если
2 —Г
то
м
«11 I
А
~\—\ 3
—И> !)•
145.

Пример. Пусть имеем квадратную матрицу
1 2 3
А —
6
10
5 6
4 6
4 5
+ 2(-1)
+ 3(+1)
8 10
+ 2(-1)
7 10
+ 3(+1)
7 8
И1 = 4+1)
= 1 (50 — 48) — 2 (40 — 42) + 3 (32
•
35) = — 3.
Здесь согласно (3.23) ёе1 (А) вычислен при I = 1 путем разложения по первой
строке. То же значение определителя мы бы получили по любой другой строке
или столбцу матрицы.
Для рассматриваемой в примере матрицы А имеем
2 4 —3 "
Л* = 2 —11 6 , А-1 = —
_3 б —3
3.13. Обратить нормальную матрицу
3 2
2
2
—3
4
—11
6
—3
6
—3
с контролем = Е.
Ответ:
(3.24)
—0,250
0,500
—0,250
3.14. Найти вектор Дх, если матрица Я имеет вид (3.24), а вектор свободных
членов
/—0.5>
ХЧ = [ —0,5
\-1,<Ъ
Ответ: выполняя вычисления согласно (3.22), находим вектор
(
0,125
—0,125
0,375
Для решения небольшого числа нормальных уравнений (3.16)
применяют еще так называемое правило Крамера, согласно которому
неизвестные
*х, = и т. д.
' ДО
2
|Й|
где —определители матрицы /?, в которой столбец К} заменен
столбцом свободных членов. Так, в условиях задач (3.13) и (3.14) имеем
146.

2
3.15. Решить по правилу Крамера систему нормальных уравнений
28*1 —
Ьх
2
+ 2 = 0;
—8*1 +28*
г
—
1
=0.
Ответ: 8*1 = — 1, 8*, = 0.
3.16. Решить по правилу Крамера и с помощью обратной матрицы систему
нормальных уравнений с матрицей
§ 29. РЕШЕНИЕ СИСТЕМЫ НОРМАЛЬНЫХ УРАВНЕНИЙ ПО СПОСОБУ
ГАУССА
Одним из эффективных и широко распространенных способов ре-
шения нормальных уравнений является способ Гаусса, который со-
стоит в последовательном исключении из уравнений всех неизвестных.
При этом исходная система заменяется так называемой эквивалентной
системой уравнений, имеющей вид
[аа] Ьху + [аЬ] Ьх
г
+ [ас] + ... + [а§] Ьх
к
+ [а1] = 0;
и вектором свободных членов
Ответ:
[66.1]8л:
г
+ [&\1]8ж
3
+ ... = [6^.1] 8*
й
+ [ЫЛ] = 0;
[сс. 2] 8*3 + ... + [С&2] Ъх
к
+ [с1.2] = 0; (3.25)
- 1)1 + - 1)] = 0.
147.

Ее получение называют прямым ходом решения. Неизвестные,
начиная с последнего, вычисляют из так называемых элиминационных
уравнений, получаемых из системы (3.25) делением на квадратичные
коэффициенты:
4 =
=
Ьх
к
=
И1 _ М.
[аа I
| Ьс.
1
[аа\
[ЬЬА]
Ц, —.
Ш Ьх
к
-
[аа] [аа]
[ЬЬ. 1]
8л: ь
[Ы.
1]
Ш- 1)]
[«•<*-1)1
(3.26)
Этот процесс называют обратным ходом решения.
Коэффициенты при неизвестных в эквивалентной системе (3.25)
называют алгоритмами Гаусса.
Правило раскрытия алгоритма Гаусса. Алгоритм с цифрой / будем
называть преобразованным, а без цифры — непреобразованным. Тог-
да любой преобразованный алгоритм Гаусса равен этому же непреоб-
разованному алгоритму минус число дробей, совпадающих с цифрой
/ раскрываемого алгоритма. Знаменатели этих дробей равны первым
коэффициентам (у—1) эквивалентных уравнений, а их числители —
произведению двух алгоритмов с той же цифрой, что и в алгоритме
знаменателя, причем первый сомножитель условно получается как
произведение первой буквы знаменателя на первую букву
раскрываемого алгоритма, а второй — как произведение второй буквы
знаменателя на его вторую букву. Например,
[ЬЬ. 1] = | ЬЬ\
[ЫЛ\ = \Ы]
И] \аЬ]
[аа]
[аЬ\ [а/]
[аа]
\с1.2] = [с/]
[ас] \а11
[аа]
[Ьс.
1]
[Ы.
1]
[Ю.1]
И т. д.
Возможна и неполная форма раскрытия алгоритма, когда рас-
крываемый алгоритм с цифрой / равен тому же алгоритму с цифрой
/'—1 минус последняя дробь из полной формы раскрытия. Например,
[с/
.2] =
[с
/.1]-ЫШ1.
'
[Ы.
I)
В индексной форме записи система эквивалентных уравнений будет
иметь вид
148.

[<
а!
1
а
118*1 + [01«г] + 1^а
3
\ 8*
3
+ ... + [а
х
а
к
] Ьх
к
+ [а
1
/] = О
[а^.1
]
Ьх
г
+ [а
2
а
3
.1 ] 8*
3
+ ... + [а
2
а
к
.
1 ]
Ъх
к
+ [а
2
/.1 ] = О
[О3О3.218*3 + ... + [а
3
а
й
.2] 8*
й
+[а
3
/. 2] = О
[а
к
а
к
.(к - 1)] Ьх
к
+ [а
й
/. (к — 1)] = О.
(3.27)
Удобнее элементы матрицы Я обозначать через ЯI}. Тогда вместо
(3.27) получим
Я
п
Ьх, + /?
12
8*
2
+ Я
13
8*3 + ... + /?
1Л
8*
Л
+ = 0;
1 ]
8*
2
+ [ Д
23
.1
]
8*
3
+ ... + [Я
2к
.
1 ]
8*
й
+ [Ь
2
.1
]
= 0;
1Я
кк
.(к-1)]Ьх
к
+ Ц
к
.(к~1)}=0.
Алгоритмы Гаусса раскрываются следующим образом:
КцНу И {*«••!] _
Яц [Л
2
,.1]
*.«*•! [Я*-! И*-*-!]
и т. д.
В дальнейшем будем пользоваться буквенной системой обозначений,
введенной Гауссом.
Заметим, что определитель матрицы коэффициентов нормальных
уравнений (нормальной матрицы) вычисляется по формуле
0 = [аа\[ЬЬЛ) . . —I)].
(3.28)
Пример. Решить по способу Гаусса систему нормальных уравнений
2,5838*! — 1,1675*2 — 0,2505*3 + 1,684 = 0;
— 1,1675*, +2,8335*2— 1.000Ц, —0,417 = 0;
— 0,2505^ — 1,0005*2 + 1,8775*
3
— 1,942 = 0-
Находим алгоритмы
[ЬЬ.1] = 2,833 - ^'т
1 = 2
'
306:
[*•!] — 1,000-
(
-
1
-
16
Л17°'
250)
= — 1,113;
[&/.!] = — 0,417-
2,583
(- 1,167) (1,684)
2,583
в второе эквивалентное уравнение
2,3065*2 — 1,1135*8 + 0,344 = 0;
алгоритмы
= + 0,344
149.

[сс.2] =1,877
(-О.ЕВО)» (— 1,113)
а
[с/.2] = — 1,942—
2,583 2,305
(—0,250)(1,684)_ (—0,250) (0,344)
2,583 2,305
1,315;
= —1,741
и третье эквивалентное уравнение
1,3158*3— 1,612 = 0;
элиминационные уравнения
8*, = 0,4528*
2
+ 0,0978*
3
— 0,652,
8*,= 0,4838*3 — 0,149,
8*3= 1,226;
неизвестные
8*,=— 0,333, 8*
2
= +0,443, 8*
3
= + 1,226.
Подстановка полученных значений в исходную систему подтверждает правиль-
ность полученных результатов.
Способ Гаусса удобен тем, что все вычисления удается располо-
жить в компактной схеме, требующей выполнения однотипных вы-
числительных действий и позволяющей контролировать промежу-
точные результаты.
Контроль составления уравнений ошибок производится вычисле-
нием в две руки.
Контроль составления и решения нормальных уравнений произво-
дится методом сумм:
а, + + с, + • • • + й + (* = Ь2 п), (3.29)
причем [а] + [6] + [с] + ... + [Д + [/] = ОД.
Коэффициенты нормальных уравнений и их свободные члены кон-
тролируют так:
[аа] + [аЪ] + . . . + [а^] + [а/] = [аз];
[08] + Ш + • • • + + 1§1] = [*«];
[аЦ + [Ь1] + . . . + [
В
1] + [И] = [&];
[ая] + [бе] +... + [*«] + [/5] = [55].
Далее:
[аа] + [аЬ] + [ас] + . . . + [ад] + Ш] = [ов];
[ЬЬА] + [Ьс.2]+ . . .+[^.1] + [Ш] = [65.1];
[сс.2] + . . . + [
С8
.2] + [с/.2] = [сз.2];
(3.30)
(3.30')
[М- (Л-1)] + (* ~ О) = (к - 1)].
Заключительным контролем прямого хода решения в схеме Гаусса
является выполнение равенств
150.

[И.к] = [1з.к] = [55.6].
(3.31)
Затем переходят к вычислению неизвестных Ьх
}
. По мере их вы-
числения контроль осуществляют путем вычисления вспомогательных
неизвестных 8х) (см. ниже).
Получив все неизвестные согласно (3.26) вычисляют по фор-
муле (3.3) поправки VI и контролируют на основе выражений
[аи] = 0; [Щ = 0; = 0. (3.32)
Проверяют также выполнение контрольных равенств
[У
2
] = [П.к\ = [/5.6]. (3.33)
Справедливы равенства
И = [Щ = [5У]. (3.34)
Окончательным контролем решения задачи уравнивания является
соблюдение равенств у
(
+ с// = Фг(*1> •••» которые сле-
дует проверить при нелинейных функциях (контролируется правиль-
ность разложения в ряд).
В линейных задачах достаточно ограничиться проверкой равенств
(3.32), (3.33).
Составление нормальных уравнений при равноточных измерениях
и их решение выполняют с помощью трех схем, приведенных для трех
неизвестных.
Схема 1
Номера
измерений
а
1
Ь
1
С
1 ч
1
<*1
Ьг
Н
к
«1
2 а
г
ь
г
Ъ «2
"г
п
<*п Ь
п
с„
«я
0/1
•
[а]
Ъх<
М
\ь\
8*.
]Ьо]
[с]
8*3
[со]
[V]
и
Схема 2
О]
Ь]
С] 5)
Контроль
1°
[аа]
[аЬ] [ас]
[а1]
[<и]
Расхождение до
*
[аа]
[ЬЬ]
[Ьс]
[Ы]
[Ьп]
0,01
[сс] [с/]
[С5]
1»!
['«]
1»!
[я]
151.
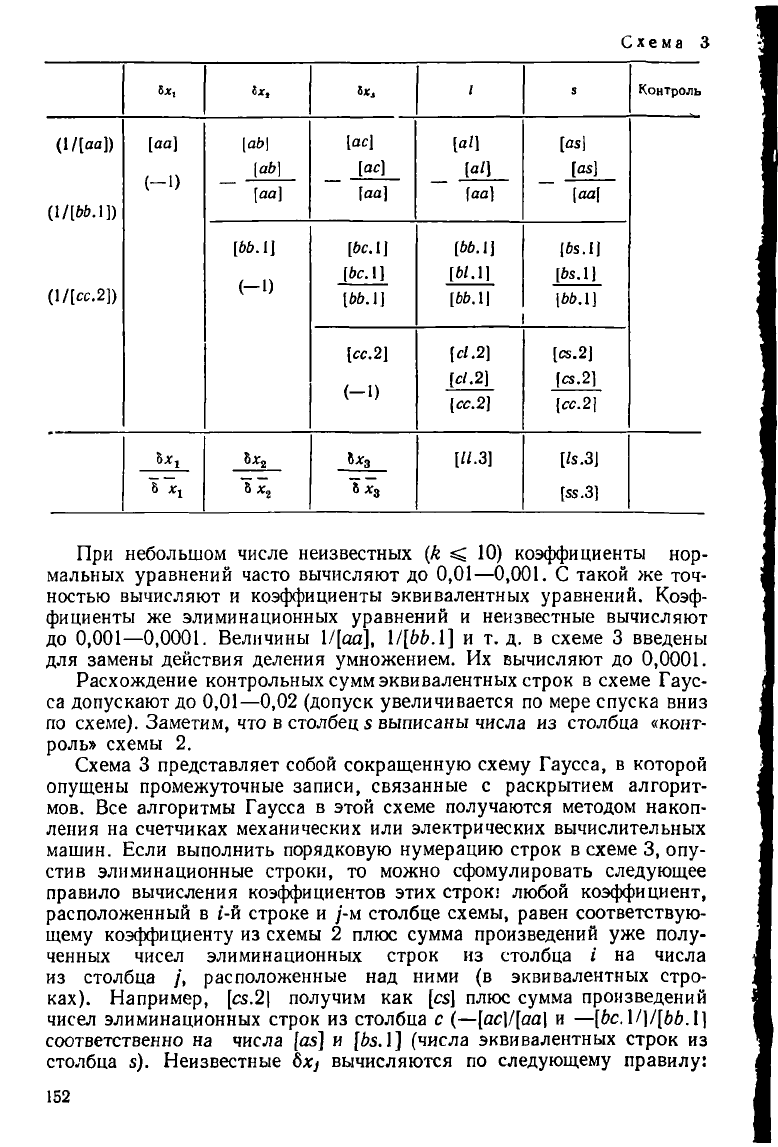
Схема 3
6*,
(х,
1
8
Контроль
(1/М)
(1ЦЬЬЛ])
[аа]
(-1)
[аЬ\
[аЬ\
\аа]
[ас\
[ас]
[аа]
[а/1
[а/1
[аа]
[а*]
[05]
\аа\
(1/[сс.2])
[66.1]
(-1)
[6с. 1]
[6с.1]
[66.1]
[66.1]
[6/.1]
[66.1]
|&5.Ц
[65.1]
|66.1]
[сс.2]
(-1)
[с/.2]
[с1.21
[сс.2]
[сз.2]
[«.2]
[сс.21
Ьх
2
[//.3]
[1з.З]
6
~Ъх
г
8 х
3
[55.3]
При небольшом числе неизвестных (к < 10) коэффициенты нор-
мальных уравнений часто вычисляют до 0,01—0,001. С такой же точ-
ностью вычисляют и коэффициенты эквивалентных уравнений. Коэф-
фициенты же элиминационных уравнений и неизвестные вычисляют
до 0,001—0,0001. Величины
1
/[аа], \![ЬЬЛ\ и т. д. в схеме 3 введены
для замены действия деления умножением. Их вычисляют до 0,0001.
Расхождение контрольных сумм эквивалентных строк в схеме Гаус-
са допускают до 0,01—0,02 (допуск увеличивается по мере спуска вниз
по схеме). Заметим, что в столбец 5 выписаны числа из столбца «конт-
роль» схемы 2.
Схема 3 представляет собой сокращенную схему Гаусса, в которой
опущены промежуточные записи, связанные с раскрытием алгорит-
мов. Все алгоритмы Гаусса в этой схеме получаются методом накоп-
ления на счетчиках механических или электрических вычислительных
машин. Если выполнить порядковую нумерацию строк в схеме 3, опу-
стив эли.чинационные строки, то можно сфомулировать следующее
правило вычисления коэффициентов этих строк; любой коэффициент,
расположенный в 1-й строке и /-м столбце схемы, равен соответствую-
щему коэффициенту из схемы 2 плюс сумма произведений уже полу-
ченных чисел элиминационных строк из столбца / на числа
из столбца /, расположенные над ними (в эквивалентных стро-
ках). Например, [с$.2| получим как [с5] плюс сумма произведений
чисел элиминационных строк из столбца с (—[ас[/[аа| и —[Ьс.\1\1[ЬЬЛ\
соответственно на числа [аз] и [Ьз.
1
] (числа эквивалентных строк из
столбца х). Неизвестные &Х] вычисляются по следующему правилу:
152
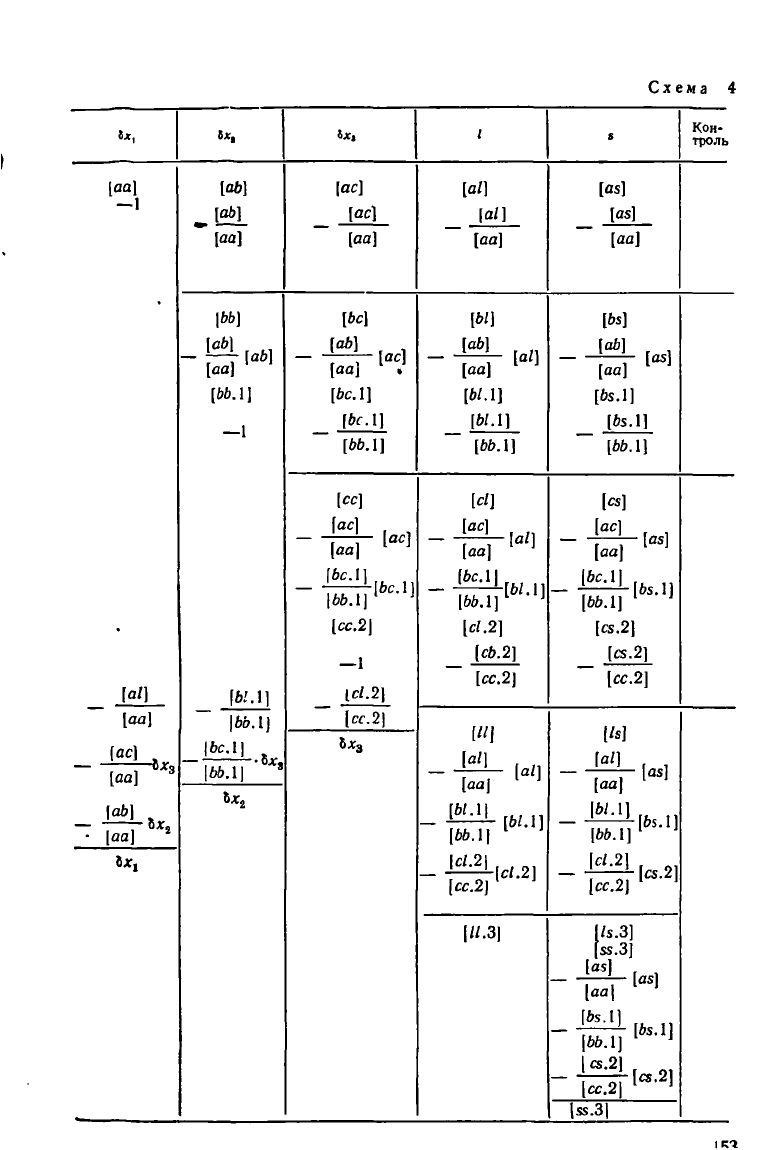
Схема
4
8дг, 1
8
Кон-
троль
[вв]
—1
[а/]
[аЬ]
ш
[вЬ]
"[аа]
[ас]
[ас]
[а1]
\а1]
[«]
[05]
[вв]
—1
[а/]
[аЬ]
ш
[вЬ]
"[аа]
[аа]
[аа]
[аа]
[вв]
—1
[а/]
[66]
[аа]
[ЬЬЛ]
—1
|6М]
[6с]
[аЬ] , .
[аа]
[6с.1]
[6с.1]
[66.1]
[Ы]
№ , „
[аа]
[МЛ]
[ЫЛ]
[ЬЬЛ]
[65]
[аЬ]
— г 1
05
[аа]
[65.1]
[65.1]
[66.1]
[вв]
—1
[а/]
[66]
[аа]
[ЬЬЛ]
—1
|6М]
[сс]
Ы
~ \
аа
\
1аС]
|66.1]
1
[сс.2]
—1
(с/,2]
[с1]
— г 1
[а/
[аа]
[6с.11
"
166.1]
[с1.2]
[сЬ.2]
[сс.2]
[а]
[ас]
- [08]
[аа]
- !
6СЛ1
[65.1]
[66.1]
[С5.2]
[С5.2]
[сс.2]
[аа]
[ас]
—
—0*о
[аа]
3
[ аЬ]
" 1 аа] *
|66.1]
|6с.1]
— т~.
[сс.2]
Щ
[аП , „
[й]
N1 . ,
[аа]
[ас]
—
—0*о
[аа]
3
[ аЬ]
" 1 аа] *
|66.1]
|6с.1]
— т~.
5*з
Щ
[аП , „
[й]
N1 . ,
[аа]
[ас]
—
—0*о
[аа]
3
[ аЬ]
" 1 аа] *
[66.1|
8
5*з
- ™
-
[&
'
Л|
[И..]
[66.1|
-
|С/
'
21
[с/.2]
[сс.2]
- м
1051
-
|6/Л1
[6,1]
[66.1]
1
[сс.2]
1
'
[аа]
[ас]
—
—0*о
[аа]
3
[ аЬ]
" 1 аа] *
Ъх
2
5*з
- ™
-
[&
'
Л|
[И..]
[66.1|
-
|С/
'
21
[с/.2]
[сс.2]
- м
1051
-
|6/Л1
[6,1]
[66.1]
1
[сс.2]
1
'
Ъх
2
5*з
- ™
-
[&
'
Л|
[И..]
[66.1|
-
|С/
'
21
[с/.2]
[сс.2]
- м
1051
-
|6/Л1
[6,1]
[66.1]
1
[сс.2]
1
'
Ъх
2
5*з
1».3|
[/5.3]
55.3]
[«1 , ,
[аа|
- К
Ъх
2
5*з
1».3|
|55.3|
1
